估算能力 適時培養

陳瑞省

估算是根據具體條件及有關知識對事物的數量或算式的結果做出大概推斷或估計，是不需要進行精確計算的口算。《2011版數學課程標準》指出，在學段目標方面，第一學段（1～3年級）在具體情境中，能進行簡單的估算;第二學段（4～6年級）能理解估算的意義，進行數量的估計，具有運算結果進行估計等方面的數感。在內容標準方面，第一學段（1～3年級）能結合具體情境進行估算，并會解釋估算的過程;第二學段（4～6年級）在解決問題的過程中，能選擇合適的方法進行估算。因此我們必須重視估算教學，如何適時培養學生的估算能力呢？筆者采用如下策略，進行了嘗試：

一、強化估算意識

估算意識是指面臨有待解決的問題時，能主動嘗試著從教學的角度適用教學的思想方法尋求解決問題的策略。具有估算意識，可以知道什么情況適宜估計而不必作準確計算，并以正確的算理為基礎，通過迅速合理的觀察和思考，在眾多信息中間尋求一批有用的或關鍵的數學信息，從而得到盡可能接近理想狀態的結果。在數學教學中，教師滲透和強化估算意識，可以進一步增強學生的學習興趣，激活學生的思維，開闊學生的思路，提高學生綜合運用多種方法處理、解決實際問題的能力。強化估算意識可以從兩方面入手

1.教學中應創設適當的情境，提出有價值的問題，使學生體會到估算的必要性。然后，鼓勵學生運用自己對數及其關系的理解對運算結果進行把握。看下面的例子：

估算餐費：除夕，小明一家人高高興興去美味餐廳吃飯，以下是這頓飯的帳單（主食免費贈送）：紅燒牛肉：25元，魚香肉絲：18元，狗肉煲：24元，青椒土豆絲：13元，清蒸桂魚：42元，炒蝦仁：36元。

（1）小明估算這頓飯不超過130元，他估算的對嗎？

（2）媽媽帶了200元錢，她帶的錢夠嗎？

這個案例來源于生活中常見的估算花費的問題，問題（1）、（2）的提出說明了估算的必要性，意在培養學生的估算意識。同時，根據不同的問題，學生應采取不同的估算策略：對于問題（1），學生只要把十位數都加起來，得到13，就能肯定這頓飯的花費一定比130元多，小明估計錯了;而對于問題（2），可以將每個數的十位都進1得到整十數（如將25看作30，13看作20）再加起來，得到190元，因此媽媽帶的錢夠了。

讓學會感受估算比具體計算有意義。教師在教學過程中有意識地滲透估算思想，用估算法對數學規律進行猜想，用估算法探尋解題思路，用估算法檢驗解題結果等，將估算思想貫徹教學始終，使學生在潛移默化中強化估算的意識。

2.讓學生盡可能地運用估算，解決一些與現實生活密切相連或精確計算較繁取得答案的問題。如“松鼠媽媽采松子，晴天每天能采20個，雨天每天只能采12個，它一連幾天采了112個松子，平均每天采14個，這些天中幾天有雨？”解答這道題時，若用估算能憑“直覺”直接得到答案，即由共采112個，平均每天采14個可以口算出總天數是8天;再由晴天每天可以采20個，個位上的數是“0”，雨天每天采12個，個位上的數是“2”，很快就能估算出雨天可能是6天，代人驗算，證實估算是正確的，且比常規解題方法來得簡便。這樣，學生的估算興趣也得到了培養。當學生產生對估算練習的興趣時，就會積極主動地去進行練習，不斷探求規律和方法，努力提高自己的估算能力。

二、養成估算習慣

著名的英國哲學家培根說過：“習慣真是一個頑強的巨大力量，他可以主宰人生”。養成估算習慣使人受益終身，但估算習慣的養成，并非一朝一夕，一蹴而就。不少教師認為，現行教材出現的估算內容少，沒有訓練的機會。其實不然，教材中估算題材是豐富的，無論是計算、解決問題，還是量的計量，只要教師用心挖掘，有目的、有意識地滲透到數學的各個環節，隨時隨“材”都可以進行估算訓練。

筆者指導學生經歷“用加法估算解決問題”的練習環節，出示練習題“電影院有650個座位，一年級有317人，二年級有330人，三年級有324人，四年級有370人，五年級有364人，六年級有326人，估一估哪兩個年級的同學可以同時看電影？學生理解思考后，自主選擇估算方法來解決問題，并說明想法。

生1：一二年級可以同時看電影，因為一年級317人可以看成320人，二年級330人，320+330=650，所以坐得下。

生2：二、三年級的同學也可以坐得下，因為把三年級324人看成320人，二年級330人，320+330=650，所以坐得下。

生3：不行，因為把324+330的和一定比650大，所以二、三年級的同學合在一起肯定坐不下。

……

筆者把例題拓展為開放性問題，為學生搭建估算平臺，使學生在多次嘗試用估算方法解決問題的體驗中，鼓勵學生應用所學知識大膽估算，并在充分交流、分析算理的過程中提高對估算方法的辨別力，使解決問題的策略數學化。長此以往，形成“會分析判斷可不可以估算，如何進行估算，用什么估算策略能更好的解決問題”，學生就能養成估算的習慣。

三、教給學生一些估算方法

小學數學中是以口算和筆算為基礎的。但估算與口算、筆算又是相輔相承的，估算反過來又能促進口算和筆算，口算和筆算是圍繞加減乘除四則運算展開的，即加、減、乘、除四種運算進行復合而成的。因此，估算的基本方法也就應包括加、減、乘、除四種估算方法，只要學會這四種基本方法，大多數的估算問題就可以解決了。估算方法很多，有的也比較靈活，筆者介紹常用的幾種方法。

1.取近似數估算法

對于一些較復雜的乘法或除法，在筆算中常以估算作為基礎，先把各個已知數四舍五入變為近似整十、整百、整千的數，就可以估算出結果的粗略的值。如估算5639÷73，被除數、除數近似于560個十和7個十，560個十÷7個十=80，所以計算結果大約是80。

2.低位估算法

即只計算算式中的最低位就能預知或用此法檢驗原式的值是否準確，此法用于驗算。如：70.2-9.9=？差的末位數字一定是“3”。

3.高位估算法

即只計算算式中幾個已知數的最高位，然后根據最高位的運算結果估計算式的值的正確率。如：6497÷51，因6497≈6500，51≈50，從6500÷50=130中，可判斷商的最高位是否正確。

4.根據常用規律估算法

如502×1.1=？積一定比502大，因為一個不等于零的數乘以比1大所以積肯定大于被乘數。

5.根據常用數量關系估算法

如，超市把每千克8.2元的奶糖15千克、每千克6.5元的水果糖15千克、每千克5.6元的酥糖22千克混合成什錦糖，什錦糖每千克多少元？（得數保留兩位小數）這類平均數問題學生往往容易出錯，但如果估算預測一下，結果便會明朗起來。就有部分學生列式：（8.2×15+6.5×15+5.6×22）（15+15+22）≈6.61，因為什錦糖的價格應在5.6元至8.2元之間，如果超出這答案毫無疑問是錯誤的。此法多適用于應用題的解答和檢驗，即根據題中已知、未知條件和所求問題，分析數量間的關系，預測或檢驗該題目中的計算結果。

6.根據生活常識或經驗估算法

生活中許多經驗、常識也有助于估算。比如：行了相同的路程，速度快的用時少，速度慢的用時多;樹的棵數、人數、球的個數、動物的只數、圖書本數等表示物體個數的數必須是整數;合格率、出勤率、發芽率都小于或等于100%，……

7.口算估算法

在計算中，除了必須熟記加法表和乘法口訣外，記住一些特殊的數的計算結果，對于估算也十分有益。如25×4=100、125×8=1000、7×11×13=1001等。

四、重視估算能力與其他思維能力的結合

估算是在弄清道理的基礎上，有的放矢地進行思考和計算。估算能力的形成要以其他思維能力為基礎，只有發展了這些能力，才能有效地鍛煉和培養估算能力。這些能力如下：

1.觀察力

在數學中，對數字特征的敏銳觀察力，是學生對已知數字進行估算的前提如6315÷71=？被除數、除數近似于630個十和7個十，630個十÷7個十=90，

所以計算結果大約是90，如果計算結果是60多就可以判定計算錯了。所以估算是一種很有價值的驗算方法，還可以通過判斷、比較大小、選擇題等不同題型練習來培養學生的觀察力。

2.直覺思維能力

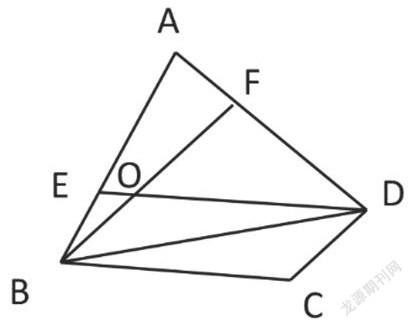
直覺思維是指對一個問題未加逐步分析，僅依據內因的感知迅速地對問題答案做出判斷、估算、設想等。由于小學生的思維特點，在他們的解題過程中常常出現一些直覺思維的苗子，教師要善于誘導和鼓勵。如學習了面積單位以后，教師可以引導學生對教室有多長、籃球場有多大、1本書有多重，憑借直觀感知進行估算。又如有一道圖形題：在四邊形ABCD中，

AB=3BE，AD=3AF，平行四邊形BODC的面積是

69平方厘米，四邊形AEOF的面積是（?）

平方厘米（如圖）。這是一道難度較大的題目，學生獨立練習后，筆者所教的兩個班每班只有大約有十人做對，通過反饋可以知道，大部分做對的學生是通過觀察、估算：我看四邊形AEOF的面積大約和三角形BOD的面積一樣，也就是69÷2=34.5（平方厘米）。接下來教學驗證了這些同學的估算是正確的，這樣就讓學生親身感受估算的威力，享受估算的喜悅，有效地激發學生的估算興趣。

3.靈活思維能力

指的是善于從不同角度和不同方面進行分析思考，善于根據條件與問題的變化而轉換思路與方法，例如比較和的大小，按一般方法需先通分才能比大小，但是根據“大半大于，小半小于”的方法，進行估算就很簡便，經常進行這樣的訓練，學生的思維就會越來越靈活。

4.分析綜合能力

通過有關估算及其應用的教學，可以培養學生分析題目的條件和所求問題，選擇合適的估算途徑和方法的能力，其中最重要的是分析綜合的能力。

數學中，教師只有將有關估算的內容，適時、適量地穿插在各個階段的計算數學中，并與口算和簡算有機地結合，才能引導學生靈活地運用估算方法進行估計，提高學生的學習興趣，提高學生的估算能力。

（浙江省龍港市第九小學）