液化氣體罐車罐體不同容積下液位高度計算

武建文 張應(yīng)龍

（甘肅省特種設(shè)備檢驗檢測研究院）

我國資源的分布與工業(yè)水平發(fā)展的不平衡，導(dǎo)致了大量的液化氣體需要長距離的運(yùn)輸，其中液化氣罐車是眾多運(yùn)輸工具中使用最廣泛的運(yùn)輸設(shè)備之一。 罐車的罐體本質(zhì)上就是一臺臥式容器，目前已經(jīng)有很多的方法可以計算臥式壓力容器不同液位高度所對應(yīng)的容積［1～5］，但對求解任意容積下的液位高度都很少涉及。 筆者通過微積分的方法推導(dǎo)出罐體容積與液位的關(guān)系，利用數(shù)值算法求解了罐體任意容積下的液位高度，為現(xiàn)場判斷不同容積下的液面高度和液位計的準(zhǔn)確度提供理論依據(jù)。

1 計算公式推導(dǎo)

為了方便計算罐體容積V，公式中的液位高度H 都從罐體底部開始算起。由于常見的液化氣體罐車的封頭有橢圓形和球形兩種，所以只需推導(dǎo)含這兩種封頭的罐體容積與液位高度的關(guān)系方程。

1.1 筒體計算公式

罐體的筒體結(jié)構(gòu)如圖1 所示。

圓心為O（0，0）、半徑為R 的筒體截面圓的

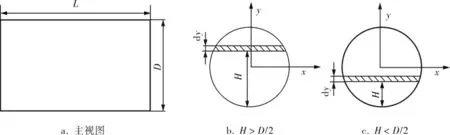
標(biāo)準(zhǔn)方程為：

按照圖1 取微元dy積分，得筒體容積的計算式：

1.2 球形封頭計算公式

罐體都有兩個封頭，將兩個球形封頭結(jié)合在一起就是一個完整的球體，如圖2 所示。

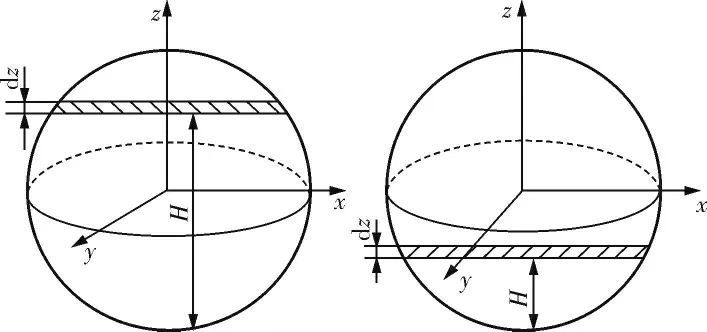
圖2 球體示意圖

故球體容積與液位高度方程式為：

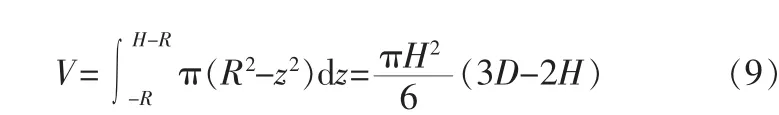
1.3 橢圓形封頭計算公式

將兩個橢圓形封頭結(jié)合在一起就是一個完整的橢球體，如圖3 所示。

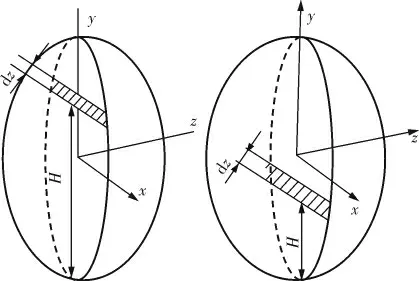
圖3 橢球體示意圖

故1/2 橢球體容積與液位高度方程式為：

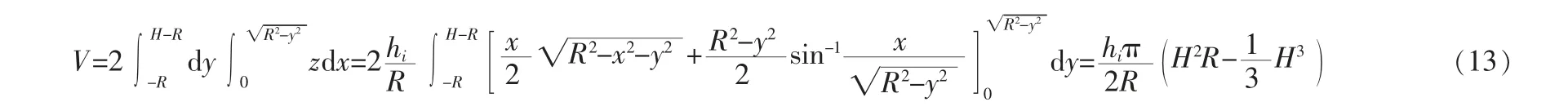
2 罐體容積與液位高度方程

將以上方程式整合，得到含球形封頭、橢圓封頭和標(biāo)準(zhǔn)橢圓封頭的罐體容積與液位高度方程式分別為：

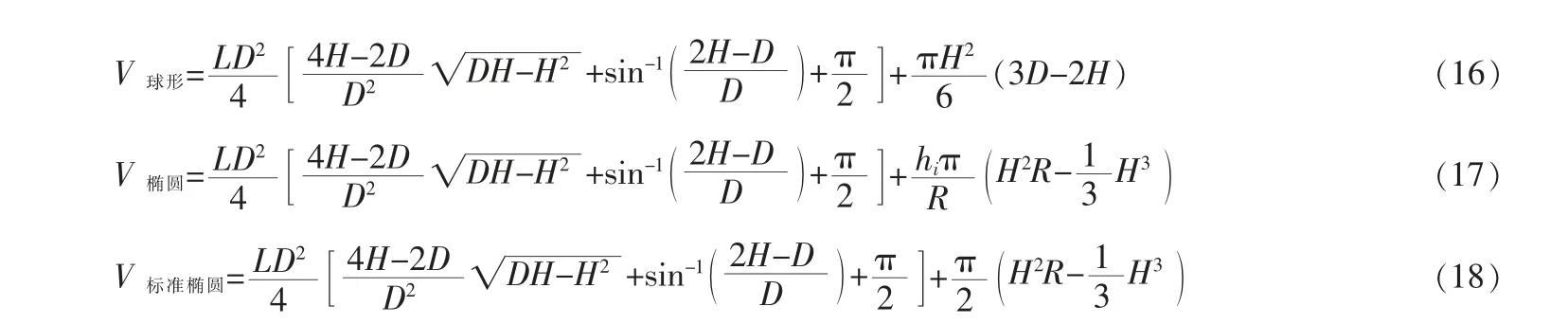
3 方程求解方法

3.1 二分法

二分法是以區(qū)間的中點(diǎn)先進(jìn)行試算，不斷地縮小求解區(qū)間，直到達(dá)到求解精度，即求出所需的解。 求解主程序如下：

3.2 牛頓法

牛頓法也稱切線法，在求解時需預(yù)先給定一個初值x0，然后不斷地迭代求解，直到達(dá)到求解精度。 求解程序如下：

牛頓法雖然可以求解， 但初值的給定太關(guān)鍵，若初值不合適，會導(dǎo)致收斂速度慢或者不收斂。 為了避免初值引起不必要的麻煩，可采用牛頓下山法求解，牛頓下山法的求解方程如下：

3.3 適易求解法

二分法雖然可以求得方程的解，但充裝率K改變時（即容積改變時），需要調(diào)整求解區(qū)間，否則可能導(dǎo)致求解速度慢或者不收斂；牛頓下山法雖可方便求解，但求解速度慢，對于正常的使用也不方便。

為了方便求解和使用，先采用Matlab 軟件畫出整個罐體H（V）方程的曲線，畫曲線時盡量用小間隔，這樣就能直接導(dǎo)出部分K 值對應(yīng)的液位高度。 對于沒有得到的少量解，可用牛頓法結(jié)合畫圖法得到的數(shù)據(jù)給定初值，就能快速求解。 因此，計算時應(yīng)采用牛頓法與畫圖法相結(jié)合的方法求解不同容積所對應(yīng)的液位高度。

4 實例驗算

以某單位制造的56.1m3球形封頭液化石油氣罐車為例，驗證以上計算方法，罐車罐體結(jié)構(gòu)如圖4 所示。

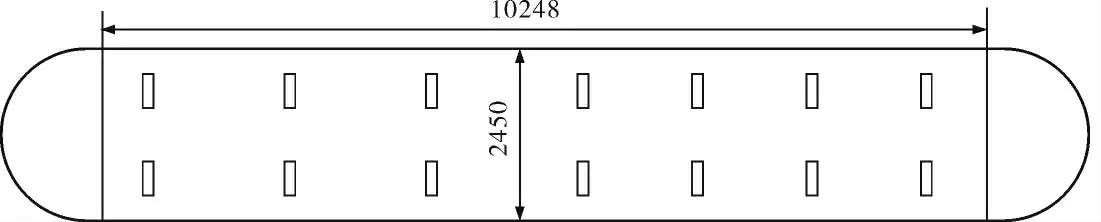
圖4 罐車罐體結(jié)構(gòu)示意圖

罐體內(nèi)部具有隔板等附件，但這些附件占有的總體積相對于罐車的容積很小，所以在計算時忽略內(nèi)部附件占據(jù)的空間。 利用二分法與牛頓法分 別 求 解K 為0.10、0.20、0.30、0.40、0.50、0.60、0.70、0.80、0.90、0.95 時的液位高度H。求解時，為了提高求解速度，設(shè)置二分法的精度為10-5，牛頓法的精度為10-8。求解結(jié)果、畫圖法繪制的罐體容積與液位高度曲線如圖5 所示。

圖5 不同求解方法結(jié)果對比

由圖5 可見，雖然二分法與牛頓法的求解精度不一樣，但求解的液位高度一樣，說明這兩種方法對求解容積與液位高度方程的近似解是等同的。 以K=0.50 為例，其近似解與理論解的相對誤差為：

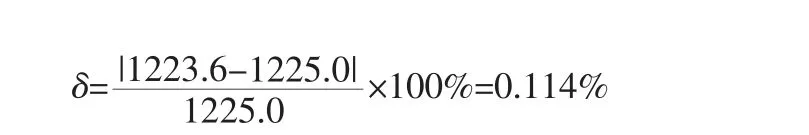
故此誤差完全能夠滿足現(xiàn)場使用及其工程的需要。

5 結(jié)束語

用微積分的方法推導(dǎo)出了橢圓形封頭和球形封頭的罐體容積與液位高度的關(guān)系。 借助軟件用二分法、牛頓法分別求解了特定罐體不同充裝率所對應(yīng)的液面高度，得出牛頓法結(jié)合畫圖的方法能快速求解此方程，并且能夠滿足現(xiàn)場使用。