我國進出口總額的時間序列分析

白同元 許萍 陳韻潔

摘 要：進出口總額是反映我國對外貿易的重要指標之一，為探索我國的進出口金額變化情況，選取我國2000～2019年進出口總額的月度歷史數據為研究樣本，采用時間序列檢驗方法對其進行了相關分析，建立相應的季節性ARIMA模型和Holt-Winters指數模型，運用所建模型對2020年進出口總額進行預測，并對兩模型精度進行分析以說明模型的可靠性。研究結果表明：我國月度進出口貿易總額時間序列預測模型表現出明顯季度性變化特征，通過模型精度對比，季節性ARIMA模型預測精度較高，結合預測結果可用于有關外貿等方面政策的制定，推動我國經濟的進一步發展。

關鍵詞：進出口總額;季節性ARIMA模型;精度分析

0 引言

隨著世界經濟的飛速發展，我國已實現了經濟全球化發展，我國的對外進出口總額從1978年的206.4億美元快速增長到2019年的45778.9億美元，進出口額成為衡量我國經濟發展的重要指標，為探索進出口額的變化規律及趨勢，采用ARIMA模型對進出口額進行合理的預測，對未來進出口發展制定相應措施，實現經濟的進一步飛躍，具有重要的理論意義。

隨著各國之間的貿易總量不斷增長，國內外學者針對進出口額與經濟發展之間的關系、進出口總額預測，進行深入的研究。國外學者Balassa通過分析1960年至1973年11個國家的GDP和進出口數據，結合其他影響因素，利用回歸函數分析GDP增長率與出口增長率之間的關系;Dollar利用1976年至1985年92個國家的數據建立回歸函數，判別各經濟指標與進出口貿易總額之間的關系;Garrison通過分析1970年至1990年86個國家的進出口數據和經濟增長頻率，得出進出口額可以推動本國經濟快速增長的理論。姚麗芳通過對2001年進出口總額數據的分析，得出出口可以推動國家經濟的增長。程蘭芳基于ARIMA模型完成對我們進口額模型的建立，結合多種影響因素，得到我國未來短時間內服務貿易進出口額的預測結果;敬久旺利用1995年至2010年我國海關進出口商品總值月度數據，采用SAS軟件建立ARIMA模型，模型的預測精度較高，通過數據充分反映我國進出口商品總值的變化規律;王春芝利用我國2001年1月到2001年9月的進出口總額，采用灰色模型完成對我國進出口貿易的短期預測;田麗采用徑向基網絡預測我國進出口總額，模型的準確率高于線性回歸模型和BP神經網絡。

本文選取從2000年1月到2019年12月的進出口總額的數據，對進出口總額進行預測。首先建立ARIMA模型進行預測，通過對比模型的AIC值，選取最優模型，完成對2020年數據的預測，結合預測的結果，對進出口貿易的發展提出相應的建議。

1 數據來源及描述性統計

本文中的數據來源于國家統計局網站，選取了2000-2019年共240期的進出口總額的月度數據。以月份為x軸，對應的進出口總額為y軸，單位為億美元，繪制折線圖，如圖1。

2000-2007年，我國的進出口總額增長趨勢較為穩定，而2008年受到全球金融危機的影響，我國的進出口總額出現較大的波動，雖然對我國的對外貿易造成了一定的影響，但并沒有改變我國對外貿易長期增長的趨勢，隨著國家的戰略政策的實施，內、外需求都得到全面的提升，我國的進出口總額增長速度不斷加快;2015年后，由于中國勞動力等多種因素影響，導致成本不斷上升，我國的進出口總額出現大幅的波動;從2017年后，受國家的外貿政策影響，我國的進出口總額不斷增長，進出口總額不斷創新高。

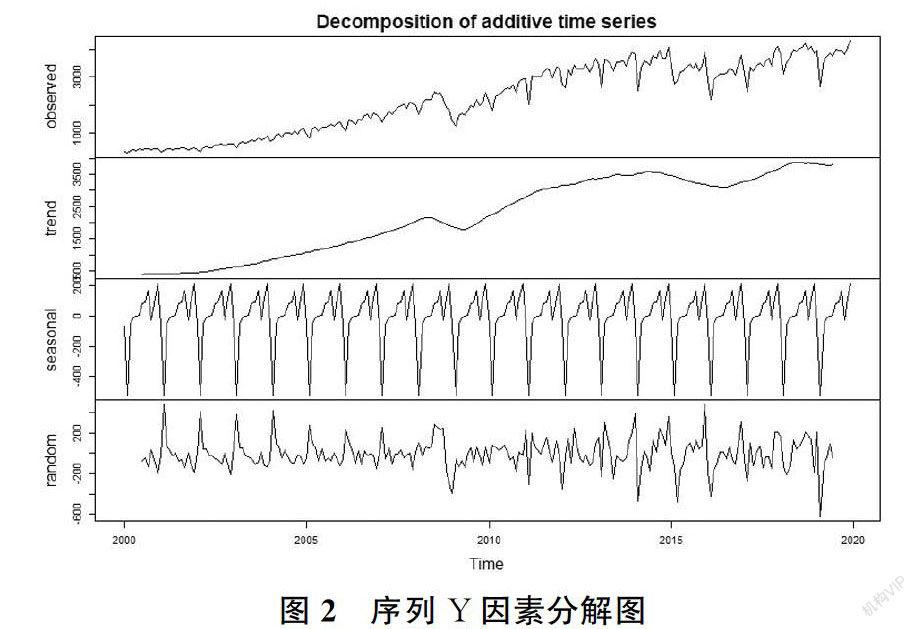
從圖1中可以看出我國的進出口總額有增長的趨勢，并對序列進行因素分解，從圖2可以看出，序列存在季節效應因素，且有上升趨勢，說明數據是非平穩的，分解圖如圖2。

2 建立時間序列模型

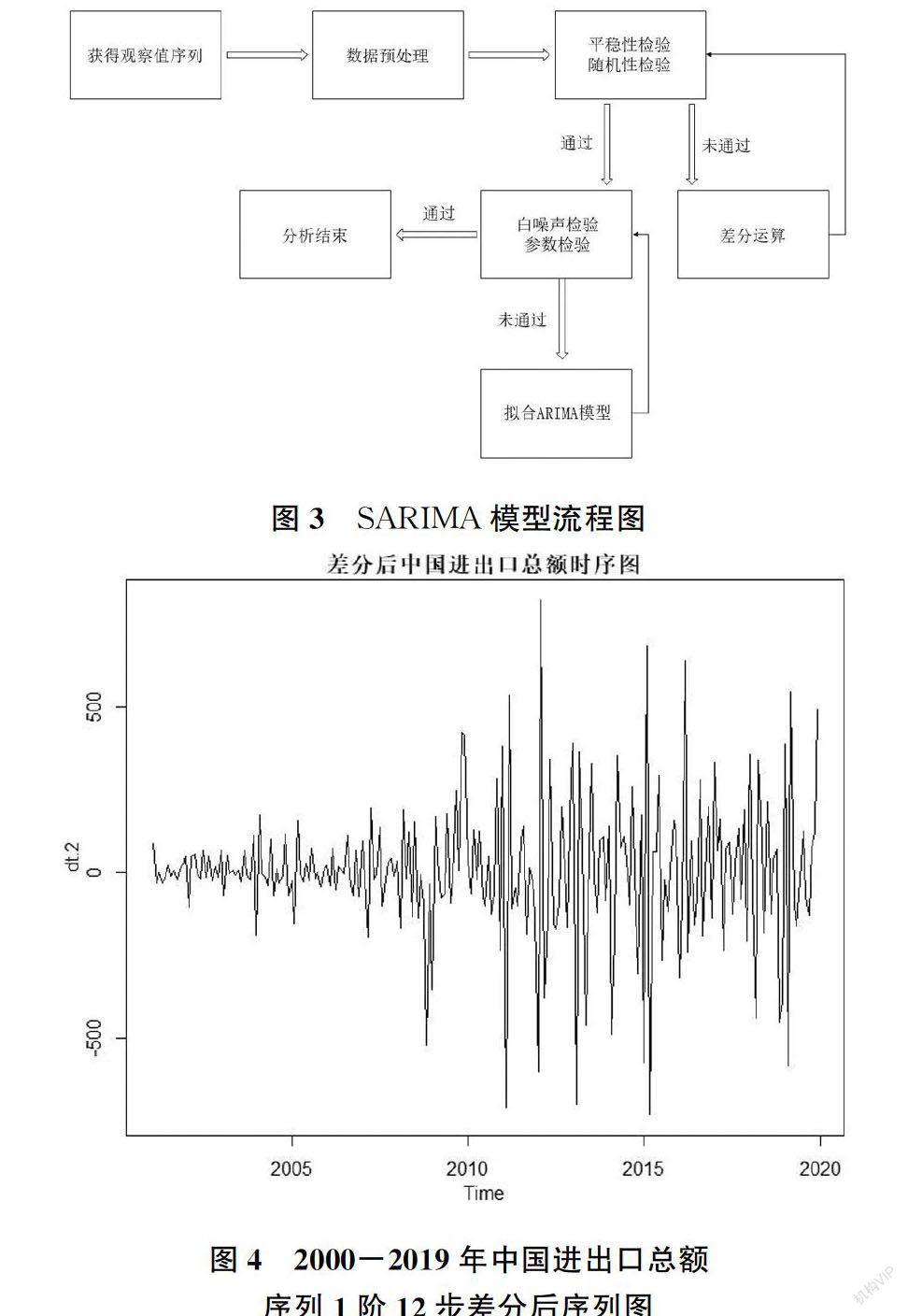
針對數據呈現時間性、季節性、趨勢遞增的特點，基于ARIMA理論建立時間序列預測模型。ARIMA模型的建立流程，如圖3。

從圖2可以看出，數據受時間趨勢影響明顯，屬于非平穩的，有必要對數據進行差分處理，提取線性遞增趨勢，提出時間影響，由此進行1階12步差分處理，得到新的序列DY，差分后圖像如圖4。

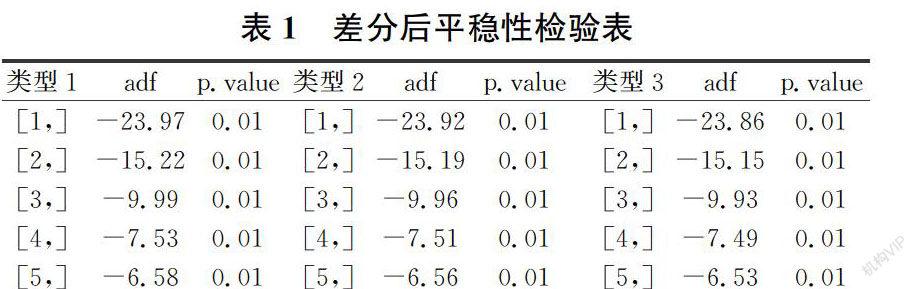
從圖4可以觀察到差分后的序列DY在一定范圍內上下波動，趨勢性消除，故對該序列進行差分后單位根檢驗和差分后純隨機性檢驗，從表1可以看出，p值均小于0.05，此時拒絕存在單位根的原假設，證明序列DY是平穩的。同時，對模型進行純隨機性檢驗，6階p值為1.67E-08，12階p值為5.29E-11，p值均遠遠小于0.05，則該序列為非白噪聲序列，通過上述檢驗可知，DY為平穩非白噪聲序列，可以進行SARIMA模型建立，結果如表1。

根據序列DY繪制自相關圖和偏自相關圖，如圖5。從短周期觀察可得，自相關圖在1階后截尾，偏自相關圖在2階后截尾;從長周期可得，自相關圖拖尾，偏自相關圖在2階后截尾，因為該序列的短期相關性與季節效應有復雜的關聯性，不能簡單提取，故嘗試擬合乘積季節ARIMA模型（p，d，q）（P，D，Q）模型，由于序列進行一階十二步差分，因此，q、d、D均為1，P為2，s為12，為了尋找最優的擬合模型，p分別選取1，2進行試驗，可供選擇的模型組合有：（1，1，1）（2，1，0）、（2，1，1）（2，1，0）。

3 模型優化

兩個模型均滿足純隨機性檢驗和參數顯著性檢驗，且模型擬合程度較好，對比兩模型結果，第二個模型的AIC和BIC的值較小，故選擇（1，1，1）（2，1，0）的SARIMA模型，模型參數如表2。

4 模型擬合效果及預測

對SARIMA模型（1，1，1）（2，1，0）進行參數估計，得到模型表達式，如式：

通過擬合的SARIMA模型（1，1，1）（2，1，0），對2020年的數據進行預測，并結合真實值對模型的誤差值進行計算（因2020年受疫情影響，導致2020年1月、2月的數據缺失，12月數據還未更新），結果如表3。