基于遷移學習的電力負荷預測研究

陳雪薇張繼東 田園 王振宇 徐正安

摘要：電力負荷預測是智能電網建設的基礎，對我國未來碳計量工作具有重要作用。基于智能算法的電力負荷預測需要大量的歷史數據作為模型訓練樣本，而新建城區或電力計量基礎較為落后地區，難以收集大量準確的歷史數據用于訓練模型，導致難以準確進行電力負荷預測。現通過深度學習網絡構建電力負荷預測模型，并基于遷移學習算法構建既有建筑電力數據和新建建筑電力負荷間的聯系，通過既有建筑負荷歷史數據訓練所得模型來預測新建建筑電力負荷，以南京市某辦公建筑為例驗證所構建的負荷預測模型，預測誤差可保持在7.8%以內，所提出的電力負荷預測方法可為實際電力負荷預測計量提供參考。

關鍵詞：電力負荷預測;深度學習;遷移學習;建筑能耗

0 引言

電力負荷預測是智能電網的基礎性功能，對未來智慧城市發展具有重要作用，對城市穩定高效運轉具有重要意義，直接影響城市未來發展和人民生活水平的提升[1]。同時，電力負荷預測有助于碳計量工作的開展，是實現我國2060碳中和大計的重要環節[2]。然而，基于現代智能算法的電力負荷預測需要大量的歷史數據作為模型訓練的基礎，而對于新建城區或電力計量基礎較為落后地區，難以收集大量準確的歷史數據用于訓練模型，導致難以準確進行電力負荷預測。

本文針對這一難點，研究基于遷移學習的電力負荷預測模型，以兩個大型辦公建筑為例，首先基于已有大量歷史數據的既有建筑負荷，使用深度學習算法構建電力負荷預測模型，再利用新建辦公樓的有限數據結合遷移學習算法，通過遷移學習算法挖掘電力負荷和影響因素間的特征關系，構建新型建筑的電力負荷模型。

本文算法可以在歷史數據不足的情況下構建智能預測模型，為新建城區或電能計量基礎較為落后地區準確預測電力負荷提供參考。

1 電力負荷預測概述

電力負荷可以認為是隨機的時序數據，也可以當作受其他特征影響的函數，前者可處理為時序預測問題，而后者可認為是回歸分析問題。因此，常用的時序預測與回歸模型都可以用于電力負荷預測[3]，例如以自回歸移動平均模型與多變量時間序列受控自回歸為代表的時間序列模型，以支持向量機與神經網絡為代表的機器學習回歸分析方法，以及近年來廣泛流行的基于深度神經網絡的預測模型。盡管將用電量視作僅具有純粹的時序依賴來處理，即通過歷史用電數據來預測未來用電量可取得較為準確的結果，但建立決定用電量的外部因素和用電量數據的回歸分析模型可為后續電力政策調整提供更多決策依據。

實際電力負荷預測時，對于新建城區或電力計量基礎設施較差地區，準確的歷史負荷數據難以獲取，傳統的基于數據驅動智能模型難以建立。針對這一難題，采用遷移算法可有效對新建建筑用電量進行預測。

Mocanu等人[4]使用遷移學習算法構建了智能電網的無監督能量預測模型，所提出模型可實現91.42%的準確預測。

Ribeiro等人[5]考慮了建筑負荷的季節性特性并結合遷移學習算法在不同建筑間構建負荷預測模型，所提出模型可提升11.2%的預測精度。

后續科研人員不斷改進算法[6-10]，利用遷移學習算法實現不同的負荷預測。

2 基于遷移學習的電力負荷預測方法

深度學習是學習樣本數據的內在規律和表示層次，學習過程中獲得的信息可對數據進行有效解釋。深度學習由人工神經網絡組成，這些網絡以人腦中存在的類似網絡為模型。當數據通過這個人工網絡時，每個層處理數據的一個方面，過濾異常值，找到合適的實體，并產生最終輸出。深度學習模型如圖1所示，一般包括輸入層網絡、隱含層網絡和輸出層網絡，經過大量數據訓練的深度學習模型可達到理想的預測精度。

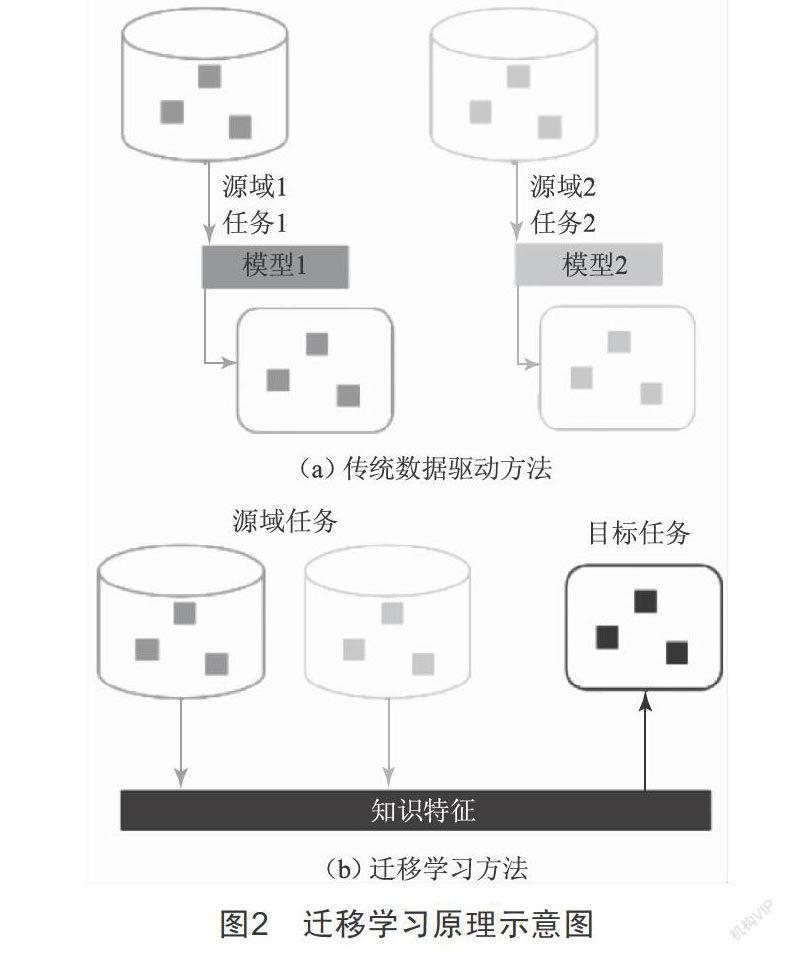
但實際工程中，訓練數據經常不足，也可能無法收集歷史負荷數據，有些應用中數據分布隨著時間推移會有變化，如何充分利用之前建立的深度學習模型，同時又保證在新的任務上的模型精度，基于這樣的問題，開展了對于遷移學習的研究，如圖2所示。圖2（a）描述的是傳統機器學習，包括深度學習過程;圖2（b）為遷移學習過程，遷移學習不僅利用目標任務中的數據作為學習算法的輸入，還利用源域中的所有學習過程（訓練數據和所建立模型）作為輸入，即通過從源域獲得的知識來解決目標任務中缺少訓練數據的難題。

基于深度學習模型和遷移學習，本文所構建的數據驅動模型首先根據既有建筑電力負荷和相關影響因素（包括內部因素：人員特征、建筑運行管理機制、室內溫度控制等;外部因素：氣象參數等）建立基于深度學習的負荷預測模型，在此基礎上，固定預訓練模型中的部分網絡參數，結合既有建筑的負荷預測模型與新建建筑的有限歷史用電數據對預訓練模型進行微調，以對其未來用電量進行準確地遷移預測，如圖3所示。

此模型可在不收集大量歷史負荷數據的基礎上實現對用電量的準確預測，為實際負荷預測任務提供便利，因此將其作為主要研究模型M1。為對比本文使用的方法，設置對比模型M2和M3，M2為基于既有建筑負荷數據的深度學習模型，M3為基于一年新建建筑歷史數據的深度學習模型。

3 結果與分析

3.1? ? 數據源介紹

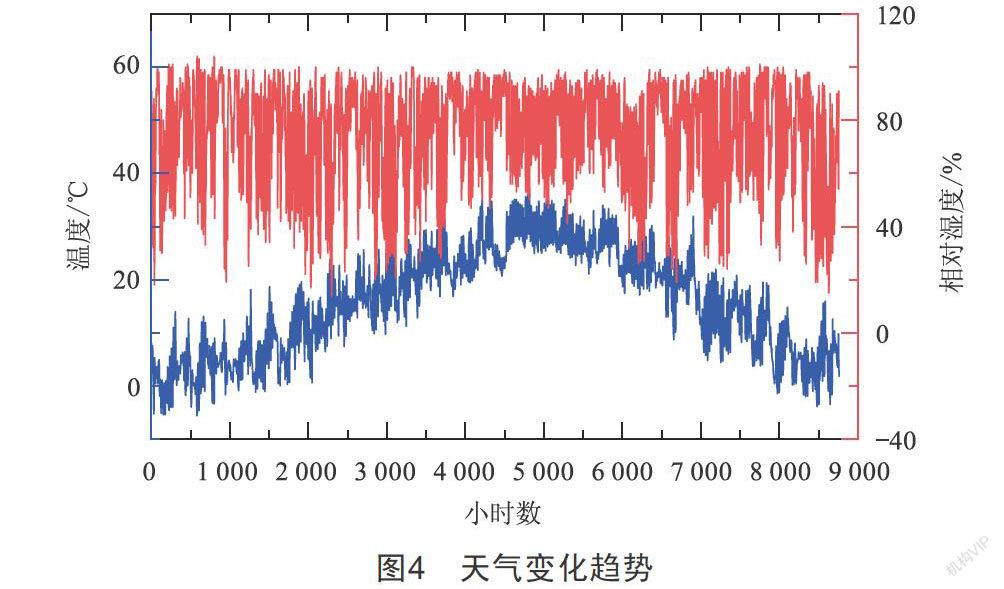
本文使用的數據集為2016—2020年南京市辦公建筑用電量數據與氣象數據的關系，數據逐時記錄，分析建筑對象分為兩類：B1為既有辦公建筑——1995年建成使用，B2為新建建筑——2019年正式使用。氣象數據涉及溫度、相對濕度、降水、風速等天氣特征，其中相對濕度、溫度均為連續數值型數據，風速用風力等級表示，云量使用離散型數據。用電量數據為計量電能表實時記錄（單位：MW）。圖4展示了南京市全年氣象參數變化趨勢。

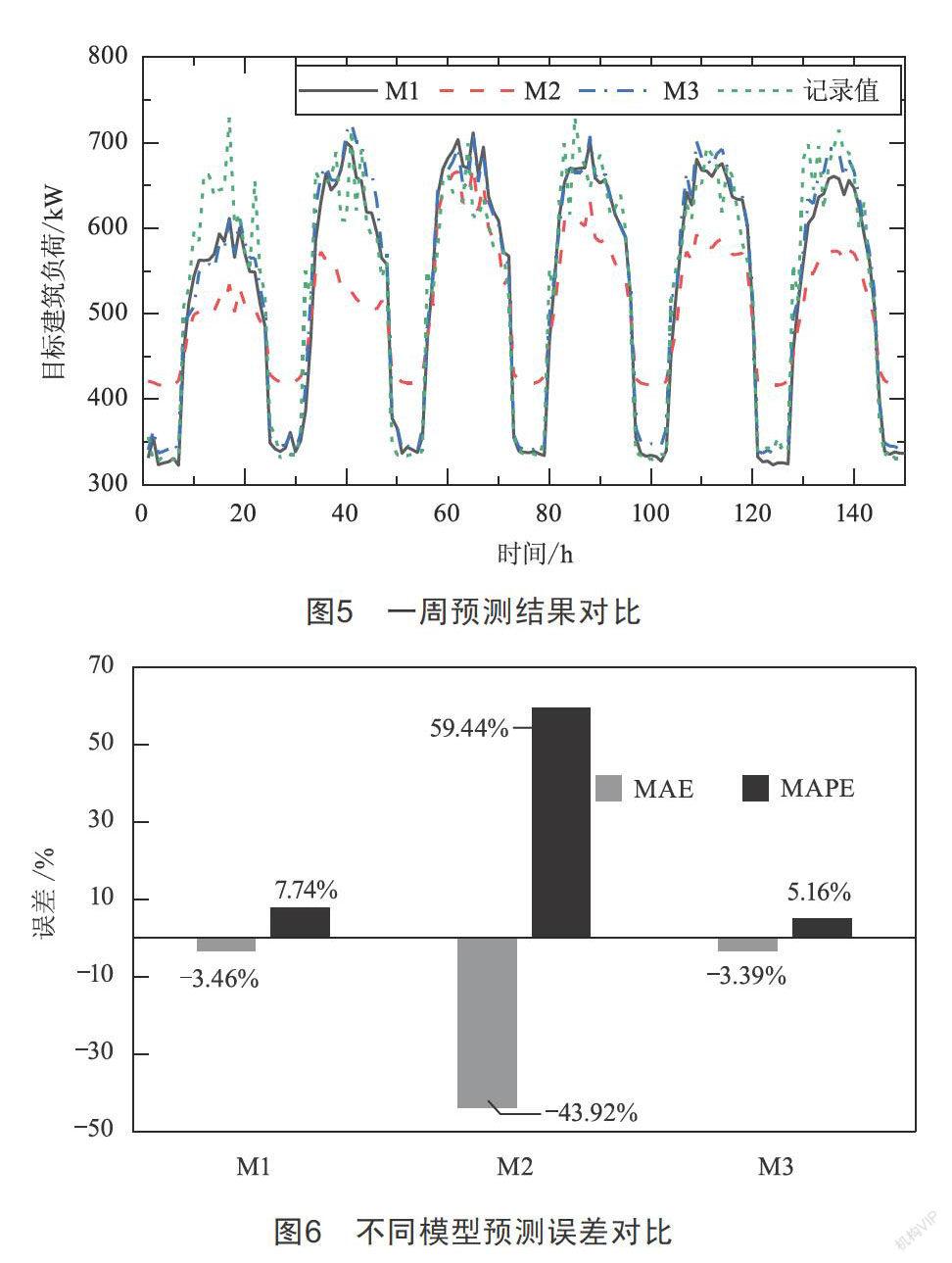
3.2? ? 誤差分析及計算配置

由于用電量是連續數值型數據，因此使用回歸模型中常用的評估方法對模型效果進行評價。考慮到用電量的實際意義，相對誤差比絕對誤差更值得關注，因此使用平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE）指標度量預測模型的效果。其計算方式為：