基于EEMD-SE和棧式降噪自編碼網絡的局部放電模式識別

張金水 蔣 偉 薛乃凡

(上海電力大學電子與信息工程學院 上海 200090)

0 引 言

電氣設備的可靠性與電網的安全運行密切相關。局部放電是造成電氣設備絕緣劣化的主要原因，也是絕緣劣化的重要征兆和表現形式[1]。由于電氣設備內部產生局部放電現象的原因有多種，其對外表現的形式也存在一定的差異[2]，常見的局部放電類型有電暈放電、沿面放電、懸浮放電和氣隙放電等[3]。局部放電狀態檢測是保障高壓設備可靠運行的重要手段，而局部放電模式識別是局放檢測的核心環節[4]。因此，對局部放電信號進行準確分類，現已成為電氣設備故障診斷中的重要部分。

國內外學者對局部放電模式識別的深入研究已經取得了一定的成果。陳新美等[5]提出了一種基于樸素貝葉斯的局部放電診斷模型，樸素貝葉斯分類器要求數據有完全的獨立性，這一點在很多情況下都難以滿足。宋輝等[6]提出了一種大數據背景下通過匹配數據庫的方法，構建出適用于放電數據的變分貝葉斯自編碼器的網絡模型，取得了較好的效果，但對于變分模態分解的重要影響參數值的選擇并未作出說明。龍嘉川等[7]引入新的頻域窗寬度計算公式，對標準S變換做改進后再提取特征進行分類，在未去噪的情況下，仍具有良好的魯棒性，但改進的S變換只適用于超高頻局部放電信號，對放電信號有一定的約束。高佳程等[8]提出了一種基于二維變分模態分解和Hilbert的特征提取方法，并將三層BP神經網絡作為分類器，但BP神經網絡屬于傳統神經網絡，需要大量的樣本訓練，而且容易出現過擬合等問題。賈勇勇等[9]針對傳統特征提取主觀性過強、準確性和魯棒性較差等問題，提出了基于深度殘差網絡的模式識別方法，該方法能夠自適應提取特征，且有較高的準確率和魯棒性，但仍存在PRPD數據無法體現氣隙放電特征導致的氣隙放電信號的識別效果較差的問題。

集合經驗模態分解EEMD是由Wu等[10]提出的一種完全自適應信號的時頻分析方法，相比小波變換等算法，EEMD不需要預先設定基函數，且對局部放電該非線性非平穩信號有獨特優勢。若將EEMD與樣本熵SE相結合可以有效解決EEMD分解后產生的高維特征數據問題，同時保留原始數據的時頻特性。因此，本文將EEMD和SE結合，提出一種應用于局部放電模式識別信號特征提取的新方法，并利用棧式降噪自編碼器SDAE對局部放電信號進行分類識別。同時，本文對局部放電信號分別進行EMD-SE、SE和EEMD-AE時頻分析，對比分析了結果。此外，本文還與傳統分類器，如反向傳播BP神經網絡和支持向量機SVM等進行了對比分析。實驗結果表明，本文方法具有較高的可行性與有效性。

1 EEMD-SE基本原理

1.1 集合經驗模態分解

EEMD是一種噪聲輔助數據分析方法，具有自適應性和完備性，而且有效克服了經驗模態分解(Empirical Mode Decomposition,EMD)中由間歇性高頻分量等因素造成的模態混疊等問題[11]。其原理是利用高斯白噪聲頻譜均勻分布的統計特性，在原始信號中加入不同的白噪聲，使得信號在不同尺度上具有連續性[12]，再對信號進行EMD分解，從而消除模態混疊。EEMD實現過程如下：

(1) 將高斯白噪聲ni(t)加入到原始信號x(t)中，得到信號Xi(t)；(2) 對信號Xi(t)進行EMD分解，得到N個固有模態函數(Intrinsic Mode Function,IMF)和一個殘余分量ri(t)；(3) 重復步驟(1)和步驟(2)，但每次步驟(1)中加入的高斯白噪聲幅值都不相同，重復M次；(4) 將M次得到的IMFi(t)和ri(t)分別做集成平均處理后得到最終的IMF(t)。

1.2 樣本熵

樣本熵是基于近似熵提出的一種新的度量時間序列復雜度的方法[13]，具有抗噪聲、抗干擾力強和一致性好等特點[14]。其計算步驟如下：

(1) 給定維數m和相容極限r等參數，并由原始數據{x(n)}={x(1),x(2),…,x(N)}重構m維向量{X(n)}={X(1),X(2),…,X(N-m+1)}，其中:

X(i)=[x(i),x(i+1),…,x(i+m-1)]

(1)

(2) 計算Xm(i)與Xm(j)的距離，即：

d=Max(|x(i+k)-x(j+k)|)k=0,1,…,m-1

(2)

(3) 對給定的Xm(i)，統計Xm(j)的數目Bi，且滿足Xm(i)與Xm(j)的距離d≤r。

(3)

(5) 同樣計算當維數為m+1時的A(m)(r)。

(6) 得出樣本熵：

(4)

根據Pincus[15]的研究，同時為了使樣本熵具有更好的統計特性，本文取m=2，r=0.2×std，其中std為原始數據的標準差。

2 自編碼器

2.1 降噪自編碼器

自編碼器(Autoencoder,AE)以無監督算法逐層訓練和優化系統參數，從無標簽的原始數據中提取高維復雜輸入數據的分層特征[16]。為了確保AE提取特征的有效性，在該基礎上Vincent等[17]提出了降噪自編碼器(Denoising Autoencoder,DAE)，讓DAE學習加入噪聲后“破壞數據”之間的深層關系，再恢復出原始輸入數據，確保了網絡的良好魯棒性。DAE的原理如圖1所示。

圖1 DAE原理結構圖

對輸入數據x進行加噪“破壞”，或是加入噪聲或是丟棄數據得到數據x′，經過函數F編碼為y，再由函數G解碼為z，z即數據x的重構，最后計算輸入數據x和重構數據z的重構誤差。

2.2 棧式降噪自編碼器

SDAE是Vincent等[18]提出的，多個降噪自編碼器構成的一種深度學習網絡，每一個DAE的輸出作為下一個DAE的輸入，直至連至輸出分類層。SDAE前向訓練各層參數時屬于無監督學習，當前向訓練結束后，采用傳統的BP算法進行有監督的訓練[19]，對整個網絡系統進行微調，進而提取更深層次、更具有表征力的數據特征。SDAE結構圖如圖2所示。

圖2 SDAE原理結構圖

3 方法設計

針對局部放電信號微弱性、復雜性及非平穩性的特點，本文首次提出了一種應用于局部放電模式識別的基于EEMD-SE和棧式降噪自編碼器的方法。首先將局部放電信號經EEMD分解成多個IMF，分別對分解出的IMF求取樣本熵，構造出每個放電類型的特征向量，將放電類型的特征向量輸入SDAE進行訓練，最后將測試樣本送入訓練好的SDAE模型，完成局部放電信號的模式識別。其模式識別流程如圖3所示。

圖3 局部放電模式識別流程

模式識別具體算法實現步驟如下：

步驟1給定添加的高斯白噪聲的標準差Nstd和添加次數NE，對信號進行EEMD分解。由文獻[10]可知，當Nstd=0.2，NE=100時，EEMD對信號分解有較好效果。

步驟2給定m=2，r=0.2×std，對步驟1分解得到的IMF分量求取樣本熵，并作為每個放電類型的特征向量。

步驟3搭建SDAE網絡。本文中搭建了一個結構為100-50-20-4的SDAE網絡，即三個DAE堆疊而成。采用KFold交叉驗證，步驟2求取的樣本熵作為輸入，對網絡進行訓練和測試。

4 實 驗

4.1 數據采集

本文實驗以脈沖電流法，構造了氣隙放電、沿面放電、電暈放電和懸浮放電四類放電缺陷類型。采集每種放電類型100個樣本共400個樣本，各類放電信號波形如圖4所示。

(a) 沿面放電信號波形圖

(b) 氣隙放電信號波形圖

(c) 電暈放電信號波形圖

(d) 懸浮放電信號波形圖

4.2 特征提取

對放電樣本進行EEMD-SE分析處理，即首先利用EEMD對樣本信號分解，然后計算各IMF相應的樣本熵，構造出局部放電缺陷類型的特征向量。其中沿面放電信號的EEMD分解如圖5所示。部分訓練集的樣本熵如表1所示，表中的標簽1-標簽4分別表示沿面放電、氣隙放電、電暈放電和懸浮放電。

圖5 沿面放電信號的EEMD分解圖

表1 訓練集樣本熵

由圖5沿面放電信號的EEMD分解可以看出，該放電信號分解為了9個IMF，即9個IMF疊加后可以完全恢復出原始沿面放電信號。對分解得到的IMF分量進行主成分分析，其中IMF1的貢獻率高達96.469 0%，IMF2貢獻率為2.333 4%，IMF3貢獻率為1.050 2%，IMF4貢獻率為0.097 5%，IMF5貢獻率為0.047 7%，即前5個IMF分量已足以表征原始放電信號的特征，又考慮到太多IMF會影響網絡模型訓練的速度，同時也為了減少實驗計算的復雜度，所以本實驗中選取前5個IMF的樣本熵作為輸入。

4.3 模式識別與分類

作為深度學習的一種，棧式降噪自編碼器具有很強的特征提取能力，且有良好的魯棒性。實驗中隨機選取340個樣本作為訓練集，60個樣本作為測試集，且訓練集與測試集數據不重疊。部分測試集的樣本熵如表2所示，測試結果如圖6所示。

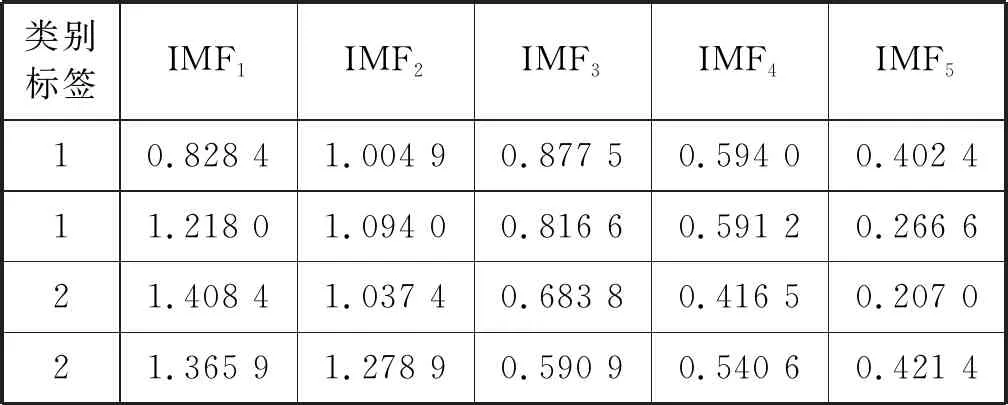
表2 測試集樣本熵

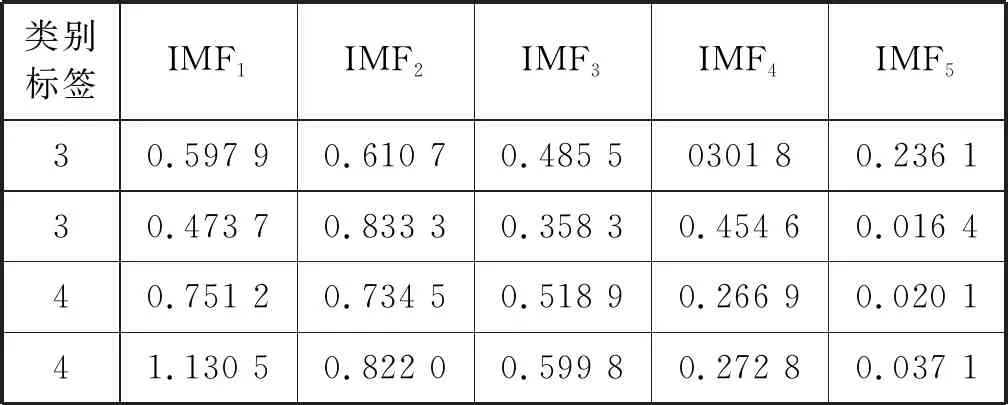
續表2

圖6 局部放電測試集識別分類結果

可以看出，60個測試樣本中只有1個樣本判別出錯，識別準確率為98.33%，充分驗證了本文方法能夠有效提取局部放電信號的特征量，并取得良好的識別效果。

為進一步驗證EEMD-SE算法在局部放電模式識別中的可行性與優越性，分別以EEMD-SE、EMD-SE、EEMD-AE和信號本身SE四種方法提取局部放電信號的特征，并對SDAE進行訓練和分類測試，對比結果如表3所示。

表3 不同特征提取方法識別準確率比較

由表3可知，基于EEMD-SE的特征提取方法得到局部放電模式識別準確率最高。由于EMD采用遞歸式分解，而且每次分解會將包絡線估計誤差傳遞給下次分解，且放電信號中或有噪聲或有間歇信號，導致出現模態混疊，影響了識別的準確率[20]。同時，EEMD-SE方法得到的識別準確率高于EEMD-AE，因為SE相比AE有更強抗噪聲能力，有更好的魯棒性，故有更高的識別率。

同時為進一步說明SDAE在處理高維大容量數據的特征提取和模式識別上的優勢，以EEMD-SE方法提取的放電信號特征作為特征向量，分別送入BP神經網絡(BPNN)、SVM、DAE和SDAE四種分類器，其對比結果如表4所示。

表4 不同分類器放電信號識別準確率比較

可以看出，SDAE網絡具有最好的識別效果。BPNN識別效果最差，這是因為BPNN作為傳統的淺層網絡其自身在處理高維大容量數據時極易產生不收斂、過擬合等問題[21]。SVM本身作為一個二分類器，其在處理多分類時較為復雜，耗時久，效果表現一般。相較于DAE,SDAE仍有較高的識別準確率，體現了SDAE深度神經網絡提取更深層特征的優秀能力。

綜合分析上述結果，相比于其他時頻特征提取算法和傳統分類器，基于EEMD-SE和SDAE的方法在局部放電模式識別中有較高的識別準確率和較強的魯棒性，充分驗證了該方法的可靠性和有效性。

5 結 語

通過分析實驗條件下的局部放電信號，本文首次將EEMD-SE算法和棧式降噪自編碼器運用到局部放電模式識別中，以EEMD-SE提取的放電信號特征作為輸入，以棧式降噪自編碼網絡作為分類器，實現了四類局部放電信號的分類識別，并得到以下結論：

(1) 首次將EEMD和樣本熵相結合的方法應用于局部放電模式識別，相較于信號本身的SE和基于EMD-SE、EEMD-AE的方法，本文方法能更有效地提取出放電信號的特征向量，且具有更高的放電類型識別準確率。

(2) 在放電信號樣本訓練及識別過程中，相同網絡結構下，棧式降噪自編碼網絡比BP神經網絡和SVM具有更強的泛化能力和更高的正確識別率。且相比單層的DAE，深層SADE網絡具有更好的放電信號特征提取能力。

(3) 實驗結果表明，本文方法能有效地提取局部放電信號的特征并快速正確地進行模式識別分類，且獲得較好的分類精度，為局部放電模式識別技術提供較為實用的解決方案。