前白棗山鐵礦地面爆破振動預測*

黃玉華，張海軍，徐國權

(1.青龍滿族自治縣發達礦業有限責任公司，秦皇島 066000；2.東華理工大學 地球科學學院，南昌 330000)

巖石開挖是采礦、隧道和土建工程中最為重要的工作環節之一。在上述工程當中，爆破是最為經濟有效的巖石破碎手段，并得到了廣泛的應用[1]。特別是在采礦工程領域，爆破對后續鏟裝、運輸、破碎等環節的成本有著直接的影響。然而，在爆破破巖過程中，炸藥爆炸所釋放出的能量只有一小部分(20%～30%)被用于破碎和移動巖石，其余能量不可避免的會以地面振動、飛石、空氣沖擊波、噪聲、粉塵和有毒有害氣體等形式對周圍環境造成不利影響[2]。在這些不利影響中，地面振動無疑是人們最為關注的，大量研究和工程實踐表明，地面振動是引起周圍結構變形、位移和破壞的主要因素。為此，研究人員在致力于提高爆破破碎效果的同時，也對爆破振動的控制進行了大量研究[3]，以避免生產爆破對巖體和附近的建筑物造成破壞。

為了控制爆破振動的危害，各個國家都制定了相應的標準[4]。因此，準確評估和預測爆破引起的地面振動已經成為許多礦山的基本要求。眾所周知，地面振動受到各種因素的影響，可以把這些因素分為兩大類，即可控的和不可控的，可控的因素主要有炸藥參數(爆速、能量、密度等)、鉆孔參數(孔深、孔徑、傾斜角度等)和爆破設計參數(孔距、排距、起爆系統、起爆順序、裝藥方式、堵塞，自由面數量等)；不可控的因素主要有巖石性質、地質條件等。一般來說，位移、速度和加速度中的任何一個都可以用來描述地面運動。其中，采用峰值質點速度(Peak Particle Velocity,PPV)來表示地面振動得到了廣泛的認可[5]。

為了評估和預測爆破引起的地面振動。在早期的研究中，研究人員試圖建立一個預報方程來預報地面振動。通過收集爆破振動數據，建立數學模型并找到數學模型中的系數，最后使用回歸算法對模型進行校準。預測方程的系數反映了巖體特性的一般規律。絕大部分預測模型都是基于兩個主要參數來進行預測的[6-9]，即最大單段藥量和從爆破點到監測點的距離。經驗模型在國際上得到了廣泛的應用，并得到了爆破工作者的認可。然而，由于爆破影響因素的復雜性，經驗預測模型還存在一定的缺陷，并不能適用于所有場所。

回顧最近的文獻表明，影響PPV的參數復雜性可以通過引入人工智能(Artificial Intelligence,AI)技術來解決。這主要是AI技術在求解非線性連續函數方面的能力，已經在工程領域得到了廣泛的應用和發展。在爆破振動預測方面，越來越多的研究人員嘗試使用AI技術作為爆破振動的主要預測方法，以替代傳統的經驗模型，并取得了很好的預測效果。Khandelwal等人使用神經網絡(Artificial Neural Network,ANN)模型對150次爆破事件的PPV和頻率進行了預測[10]，結果表明ANN模型的結果具有很高的準確率。Danial Jahed Armaghani等人提出使用自適應神經模糊推理系統(Adaptive Neuro-Fuzzy Inference System,ANFIS)和ANN兩種AI技術[11]，來對采石場爆破引起的地面振動進行預測。Fisne等人提出了一種基于模糊推理系統(Fuzzy Inference System,FIS)的預測模型對土耳其一家采石場的33次PPV監測數據進行了預測[12]，取得了很好的效果。Ghasemi等人提出了另一種模糊模型[13]，模型使用6種不同的可控輸入參數。他們還強調了模糊模型在PPV預測方面的高性能。Hasanipanah等人引入支持向量機(Support Vector Machine,SVM)模型來評估PPV[14]。Manoj Khandelwal等人使用分類回歸樹(Classification And Regression Tree,CART)模型來對PPV進行預測[15]，結果表明CART技術在預測PPV方面比傳統方法更可靠。Mahdi Hasanipanah等人提出了一個基于粒子群優化(Particle Swarm Optimization,PSO)算法的模型[16]，用于預測伊朗Shur River大壩區域爆破作業所引起的地面振動。Danial Jahed Armaghani等人嘗試使用帝國主義競爭算法(Imperialist Competitive Algorithm,ICA)來對爆破振動進行預測[17]。Erlin Tian等人基于遺傳算法(Genetic algorithm,GA)提出了兩種新的智能模型[18]，用來模擬地面振動。近年來，各種智能算法廣泛的應用到爆破振動預測領域，已經成為爆破振動預測的主要發展方向。

雖然利用AI技術對爆破振動預測進行一些研究，但沒有一種方法或模型對每個礦山都是最優的。此外，AI技術是一種需要不斷進化和多樣化的方法。在此基礎上，開發一種ANN模型來對前白棗山鐵礦爆破振動進行了預測，并與傳統經驗模型和多元線性回歸模型(Multiple Linear Regression,MLR)預測結果進行比較[19]。

1 場地條件和數據采集

現場測試是在發達礦業有限責任公司下屬的前白棗山鐵礦進行的。前白棗山鐵礦位于河北省秦皇島市青龍縣朱杖子鄉前白棗山村西南，礦區中心地理坐標為東經119°01′，北緯40°19′。礦區北西距青龍縣城8 km。區內火成巖活動頻繁，主要有花崗巖、偉晶花崗巖，其次有閃長巖、微晶閃長巖和少量煌斑巖脈侵入。脈巖對礦體起吞蝕分割破壞作用，使礦體沿走向及傾斜方向均遭到不同程度的破壞。

礦山采用淺孔留礦嗣后尾砂膠結充填采礦法，爆破作業使用YT-28型鑿巖機打上向傾斜炮孔，炮孔直徑40 mm，孔深1.8～2 m，最小抵抗線0.6～0.7 m，炮孔采用平行排列或交錯排列，網度為0.7～1 m×0.7～1 m。炸藥使用的是乳化炸藥，非電導爆管起爆。

對之前地面振動預測研究的回顧表明，單段最大藥量和爆破點到監測點的距離對PPV的影響均大于其它可控和不可控參數。以29組爆破作業的最大單段藥量(MC)和爆破點到監測點的距離(D)作為預測PPV的指標，使用的數據及其范圍如表1所示。

表 1 爆破振動數據

2 振動預測

2.1 經驗模型

為了控制爆破振動的危害，不同的研究人員根據經驗制定了各自的比例距離(Scaled Distance,SD)關系。SD是在雙對數坐標軸上記錄不同距離的PPV，并進行回歸分析，如圖1所示。本研究中使用4種在世界范圍內較為常用的經驗預測模型，并通過繪制PPV與SD在雙對數坐標軸上的回歸曲線，得到了4種經驗模型的場地系數k和b，如表2所示。

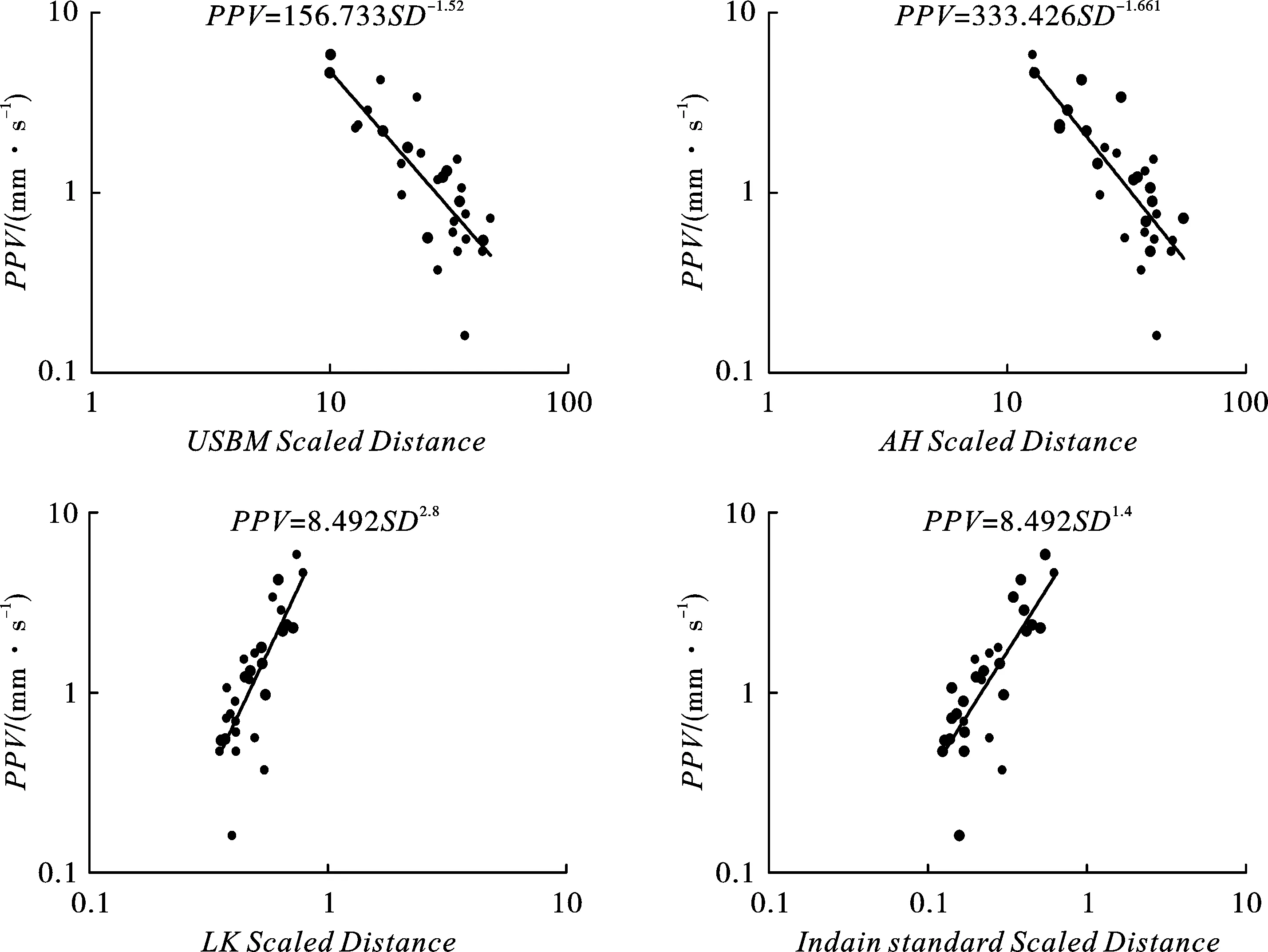
圖 1 經驗模型PPV和SD雙對數圖Fig. 1 Log-log plots between PPV and scaled distance for various models

圖2給出了不同經驗模型的預測值與實測值之間的相互關系。在本研究中，4種經驗模型的確定系數(Coefficient of determination)R2分別為0.74、0.74、0.72和0.72，USBM模型和AH模型的R2相同，且預測能力要優于LK模型和Indain模型。

2.2 MLR

回歸分析是一種統計工具，用來確定變量之間的關系。多元線性回歸(Multiple Linear Regression,MLR)是通過對兩個或兩個以上的自變量與一個因變量相關分析，建立預測模型進行預測的方法。MLR是基于最小二乘法，這意味著MLR擬合使預測值和實測值的差的平方和最小。在建立MLR模型時，使用MC和D作為模型的輸入參數來對PPV進行預測，MLR可以表示為

表 2 經驗模型場地系數

Y=β0+β1X1+β2X2+…+βkXk+ε

(1)

式中：Y是預測變量；Xk為自變量；βk為回歸系數；ε為隨機誤差。計算得到

PPV=2.182-0.052D+0.579MC

(2)

圖3給出了MLR模型預測值與實測值之間的關系，R2為0.637。

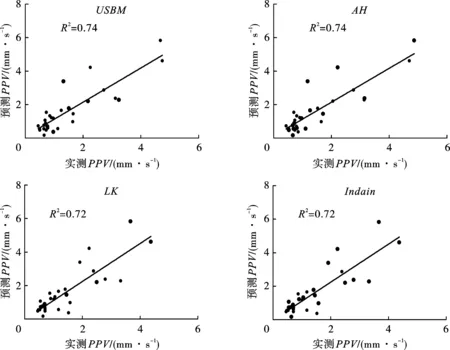
圖 2 經驗模型測量值和預測值對比圖Fig. 2 Measured vs.predicted PPV values of the Empirical model

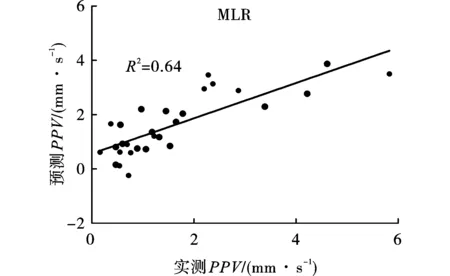
圖 3 MLR模型測量值和預測值對比圖Fig. 3 Comparison between measured and predicted PPVs by MLR model

2.3 ANN振動預測

ANN是20世紀80年以來在人工智能領域興起的研究熱點，也是目前最先進的AI技術之一。ANN起源于人類大腦的生物結構。ANN模型是由被稱為神經元的細胞構成，樹突從細胞體延伸到其它神經元，每個神經元都能接受、處理和傳輸信號。因此，ANN工作建立了輸入和輸出之間的關系。它可以從輸入和輸出數據之間的因果關系中學習，適用于求解存在多個非線性關系參數或變量間某些相關關系不易識別的復雜問題。ANN計算通常分為三個步驟，首先需要確定網絡架構，接下來是進行訓練，最后進行檢驗。

神經元的排列決定了ANN的結構，其中最常用的是多層感知(Multi-Layer Perceptron)技術。ANN中的神經元數量是有限的，它們分布在輸入層(輸入數據)、隱藏層和輸出層(計算數據輸出)中，如圖4所示。經過訓練，ANN通過調整神經元之間的數值比率來完成特定的功能。這里較為常用的是反向傳播(Back-propagation,BP)算法，BP算法有一個輸入層和一個輸出層，一個或多個隱藏層，其中權值(w)和偏差(b)在學習過程中被擬合，并分配給神經元之間的連接。

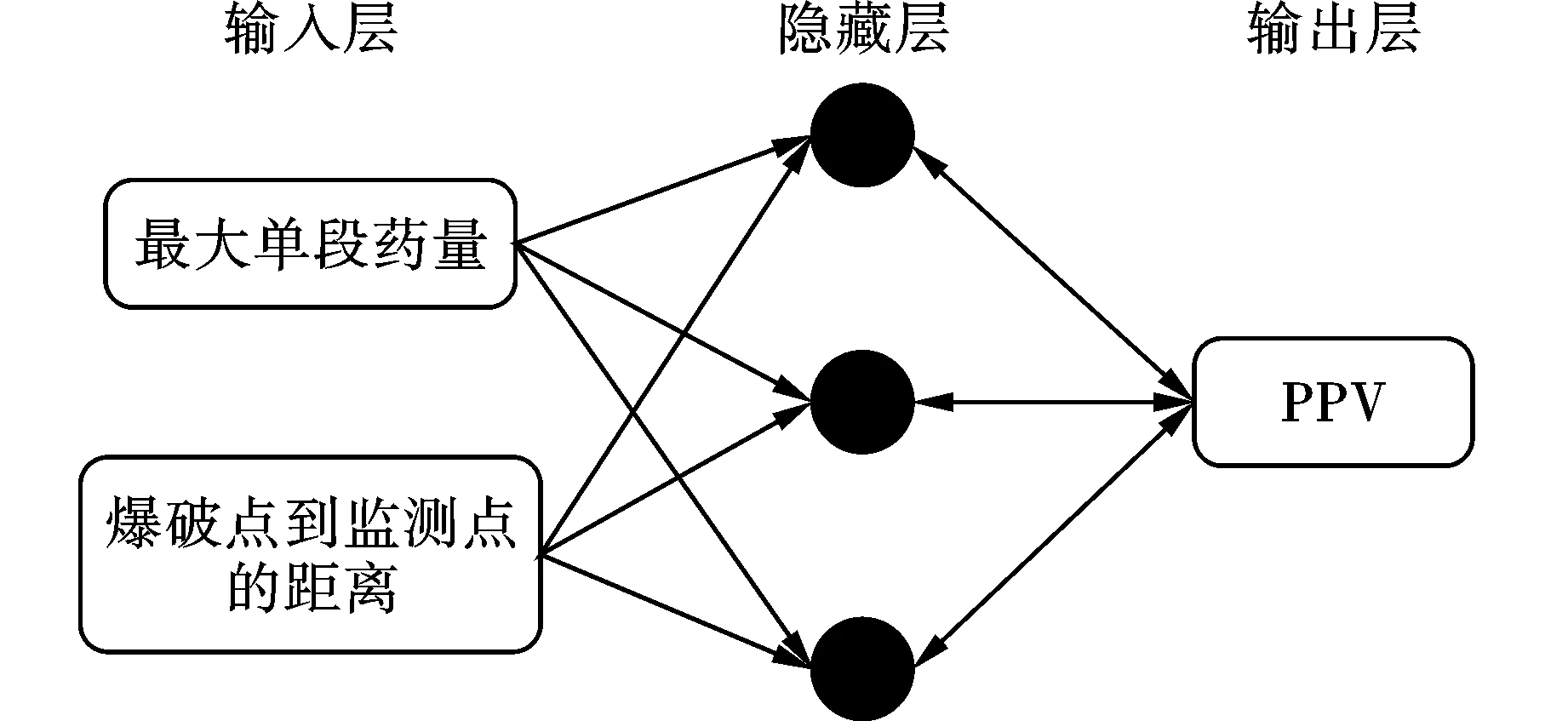
圖 4 反向傳播網絡算法爆破設計模式Fig. 4 Network back propagation algorithm for design pattern of blasting

對于ANN技術，最關鍵的問題是ANN設計。在本研究中，設計了一個包含訓練算法、隱藏層和每個隱藏層中的神經元的ANN。在設計ANN時，最具挑戰性的問題是確定隱藏層的數量和每個隱藏層的神經元數量。理論上，只有一個隱藏層的ANN可以解決實際中的大多數問題。兩個或更多隱藏層的ANN可以根據情況更好的解決問題。然而，過多的隱藏層會增加ANN的處理時間。因此，本研究采用單一隱藏層構建ANN。利用ANN作為函數逼近工具，選擇預測PPV最有效的兩個變量MC和D作為輸入變量。由于BP算法存在固有的缺陷，Levenberg-Marquardt算法可以有效克服BP算法的缺陷。為此需要對數據進行預處理，即對數據進行歸一化，隱藏層函數為sigmoid，輸出層函數為purelin。

為了訓練ANN，在采集到的29組數據中，21組數據用于訓練，4組數據用于測試，4組數據用于驗證。選擇單一隱藏層，開發了8個ANN預測模型，隱藏層神經元個數依次為3～10，最大訓練次數為1000次，訓練目標最小誤差為1e-6。利用Matlab軟件來實現ANN，通過訓練數據得到權值和偏差，同時選擇測試和驗證數據來確定網絡的準確性和有效性。停止后，根據網絡的訓練過程和測量精度，得到最終的輸出，并測試ANN模型的精度。驗證結果表明，ANN能夠很好的進行非線性回歸分析。使用R2和均方誤差(Mean Squared Error,MSE)來評價每個ANN模型的性能。表3給出了每個ANN模型的計算結果。結果表明，每個ANN模型的性能參差不齊，本研究中結構為2-6-1的ANN模型最適合用于進行PPV預測。圖5給出了結構為2-6-1的神經網絡模型的相關系數，包括訓練、測試、驗證和全部數據，且每一部分的相關系數R(Correlation coefficient)都大于0.92。

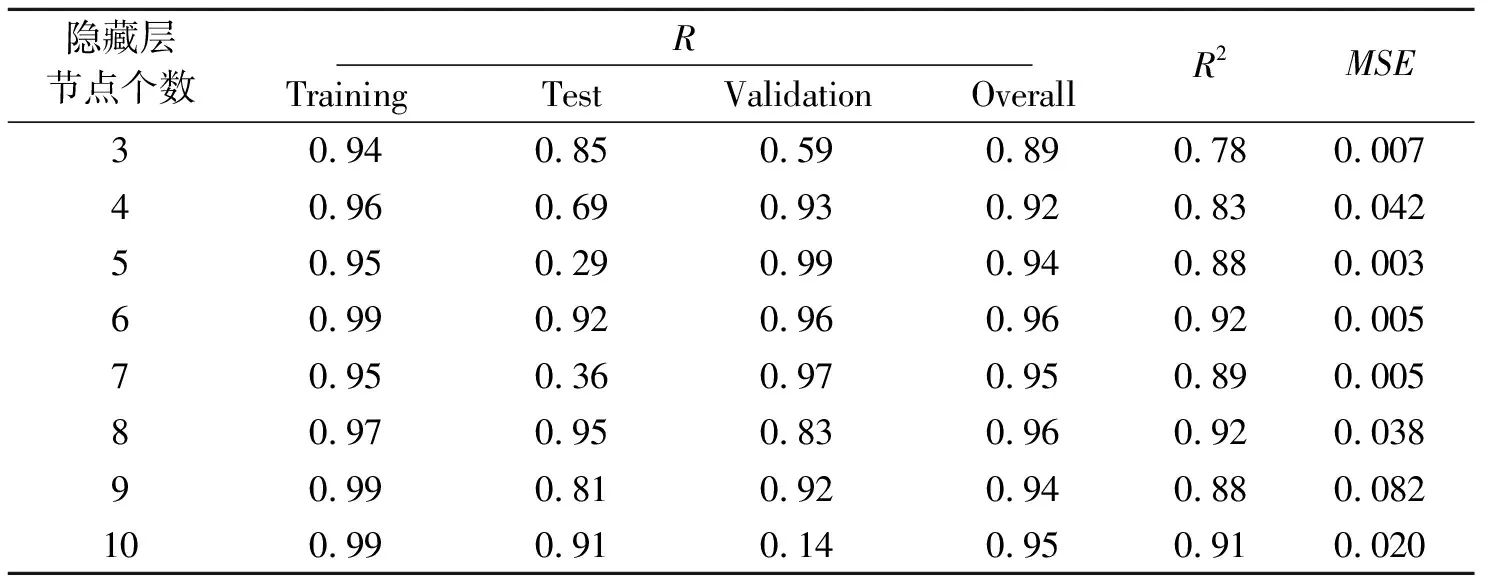
表 3 每個ANN模型的計算結果

圖6給出了ANN模型預測PPV和實測PPV之間的關系。可以看到結構為2-6-1的ANN模型R2為0.92。ANN模型預測值非常接近于實際值，且模型的預測精度可以讓人接受。

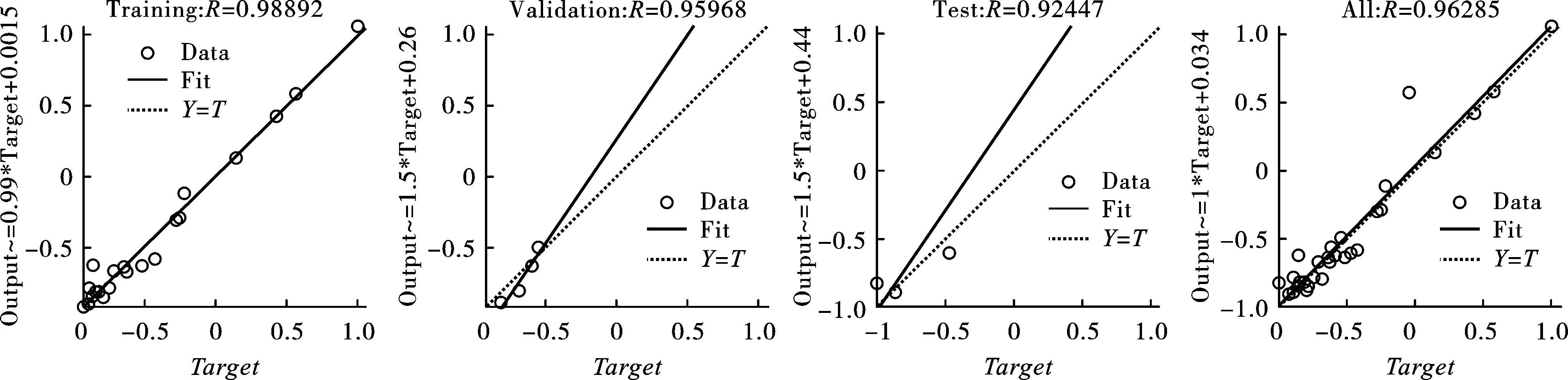
圖 5 訓練、測試、驗證和全部數據的相關系數Fig. 5 Coefficient of correlation for the training,testing,validation and overall data sets

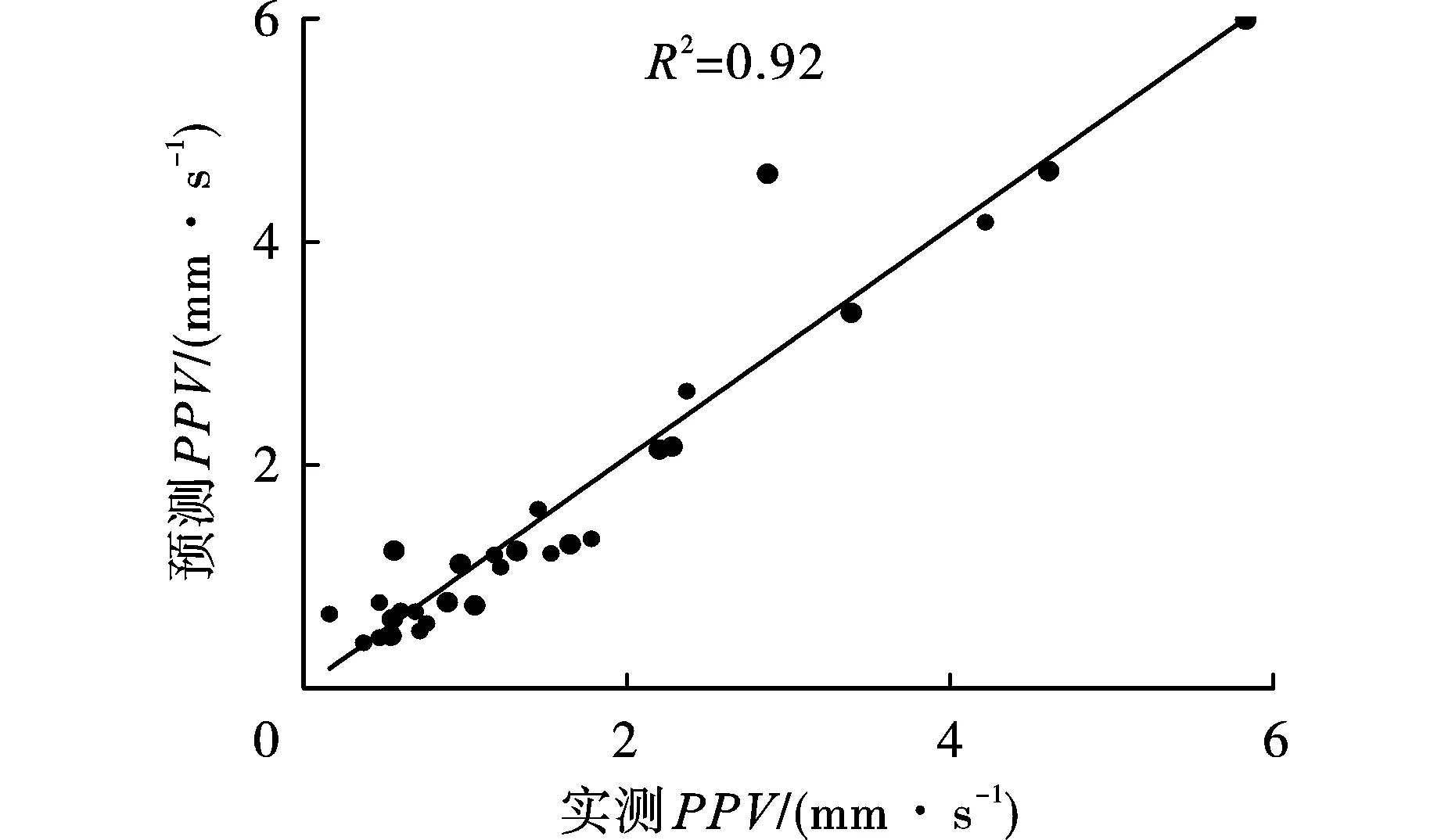
圖 6 ANN模型預測結果與實測結果的關系Fig. 6 Graph between measured and predicted PPVs by ANN model

3 性能評價指標

為了比較和評價經驗、MLR和ANN模型的性能，選擇均方根誤差(Root Mean Squared Error,RMSE)、平均絕對誤差(Mean Absolute Error,MAE)和R2作為評價指標。RMSE、MAE和R2可以表示為

(3)

(4)

(5)

4 預測模型比較

確定ANN預測模型滿足要求后，通過式(3)～式(5)對4種經驗模型、MLR模型和ANN模型的性能進行評價。經驗模型、MLR模型和ANN模型的預測性能如表4所示。可以看到，在本研究中使用，MLR模型的預測性能最低，其R2為0.64、RMSE為0.81、MAE為0.61，輸入變量的線性關系關系不明顯。由于監測數據有限，因此MLR模型在PPV預測中并未表現出很好的結果。

USBM、AH、LK和Indain等4種經驗模型預測效果相差不大，USBM和AH模型性能稍好于LK和Indain模型。大量文獻表明，USBM、AH、LK和Indain模型是世界范圍內應用較為廣泛的經驗模型，已經在世界各地成功的進行了許多研究。然而，經驗模型的有效性還沒有得到很好的評價。

對于所建立的ANN模型，可以看到，與傳統經驗模型和MLR模型相比，ANN預測數據更接近真實數據，ANN模型的R2為0.92、RMSE為0.4、MAE為0.23。計算結果表明，提出的ANN模型在PPV預測方面是可以的，模型具有較高的預測精度。

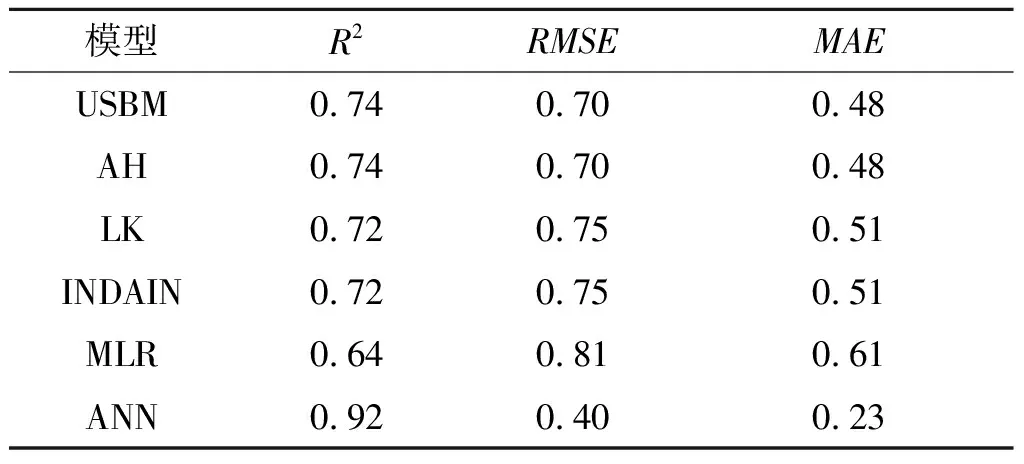
表 4 預測模型性能

5 結論

爆破是采礦工程的重要組成部分。然而，爆破產生的負面效應，特別是爆破振動，對周圍環境有著很大的影響。因此，準確預測PPV在減小爆破振動方面起著重要的作用。分別使用4種經驗模型、MLR模型和ANN模型對PPV進行了預測。結果表明，由于數據量有限，MLR模型預測效果相對較差，R2為0.64；4種經驗模型預測結果較為接近，R2分別為0.74、0.74、0.72、0.72；提出的結構為2-6-1的ANN模型預測結果最接近實際監測結果，R2為0.92、RMSE為0.4、MAE為0.23。研究證明了使用ANN預測露天和地下爆炸振動的可能性，這將確保地面振動強度可以控制在安全范圍內，使礦山爆破作業安全、高效。