中高速轉動機械結構的振動特性研究

唐剛

（中琺國際核能工程有限公司，四川 成都 610000）

隨著我國經(jīng)濟從高速發(fā)展到高質量發(fā)展的轉變，機械制造業(yè)也處于從高速發(fā)展到高質量發(fā)展的轉型變革中，在中高速轉動機械的設計工作中，需要對機械結構進行振動特性分析，并根據(jù)分析結果優(yōu)化機械結構設計，提升產(chǎn)品質量和經(jīng)濟效益。

1 概述振動特性分析和轉動機械設計工作的關系

對于中高速轉動機械產(chǎn)品，過度振動會加快機械磨損，加重噪聲污染，影響產(chǎn)品的穩(wěn)定性、安全性、使用壽命等問題，對于轉動機械的設計，振動分析越來越受到設計人員和研究人員的重視。在產(chǎn)品研發(fā)階段設計迭代次數(shù)較多，采用合理的分析方法，可以提高設計效率，節(jié)約設計成本。

2 振動特性分析在轉動機械設計中的應用原則

機械系統(tǒng)的振動往往是復雜的，應根據(jù)具體情況和要求，簡化為單自由度系統(tǒng)、多自由度系統(tǒng)等物理模型，再運用力學原理及數(shù)學工具進行分析。在中高速轉動機械設計中，轉動部件作為機械振動的來源，需要對其進行準確的振動特性分析，轉動部件一般為對稱設計，利于模型簡化，可采用理論計算。工程中只有極少數(shù)簡單的結構可以簡化為連續(xù)系統(tǒng)，對于絕大多數(shù)實際問題，需要采用近似計算方法，將分析對象簡化為單自由度系統(tǒng)或多自由度系統(tǒng)進行分析。

3 轉動部件振動特性分析的實際應用

離散系統(tǒng)振動特性的近似計算方法有多種，本文以某中高速電子轉子為例，介紹集中質量法和傳遞矩陣法的應用。對轉子進行振動特性分析時，轉子的橫向振動和扭轉振動需要單獨建立物理模型進行分析，分析思路基本一致，本文主要考察轉子的橫向振動特性。

3.1 集中質量法在轉子振動特性分析中的應用

集中質量法是將連續(xù)系統(tǒng)離散為有限自由度系統(tǒng)，是一種物理概念清晰且簡便易行的近似計算方法。本文所列轉子結構由轉軸和轉子鐵芯組成，質量主要集中在轉子鐵芯處，忽略軸承剛度和基座剛度的影響。轉子的橫向振動受轉軸的彎曲剛度和質量分布影響，模型處理時將轉子結構簡化為由無質量變截面梁和有限集中質量點組成的離散系統(tǒng)，為便于計算和對比說明，本文僅將模型簡化為單自由度系統(tǒng)和三自由度系統(tǒng)進行分析。

（1）單自由度系統(tǒng)的近似計算

單自由度系統(tǒng)模型是解決振動特性問題最簡化的形式，將轉子結構簡化為無質量變截面梁和單集中質量點的簡支梁結構，集中質量點位于轉子重心處，如圖1 所示。

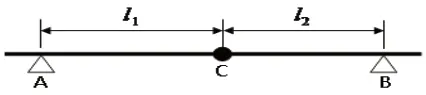
圖1 轉子結構簡化為單自由度系統(tǒng)示意圖

由柔度表示的固有角頻率求解公式如下：

對于變截面簡支梁結構，可利用卡氏定理求解某點處的柔度，卡式定理表達式如下：

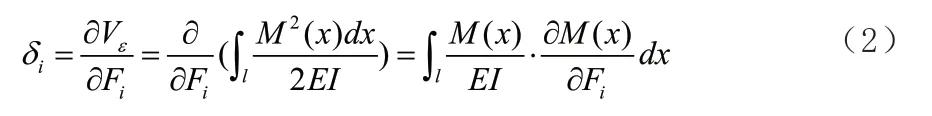
AC 段和BC 段的彎矩方程，彎矩對廣義力的偏導方程如下：

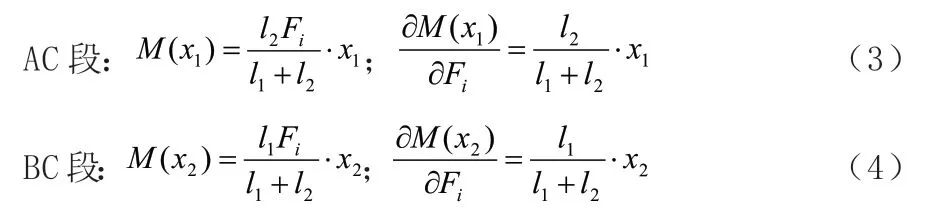
將式（3.4）和式（3.5）代入式（3.2）可得C 點變形方程。

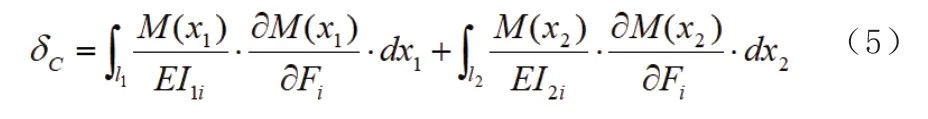
其中Ii1為AC 段各截面慣性矩，I2i為BC 段各截面慣性矩，對不同截面段分段積分，并取廣義力iF等于1，得到C 點柔度，將柔度Cδ和轉子質量m代入式（1）可得單自由度系統(tǒng)下轉子結構的固有角頻率近似計算值。代入轉子結構的相關參數(shù)求得該簡化模型下的固有角頻率為

（2）三自由度系統(tǒng)的近似計算

將轉子結構離散為無質量變截面梁和三個集中質量點的簡支梁結構，集中質量點位置分別取轉子鐵芯兩端和轉子鐵芯中心處，質量均為m/3 ，如圖2 所示。

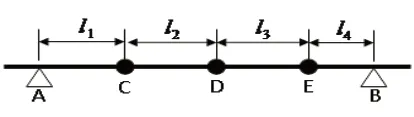
圖2 轉子結構簡化為三自由度系統(tǒng)示意圖

由柔度矩陣表示的特征方程如下：

本簡化模型將轉子質量均分在三個集中質量點處，質量矩陣為：

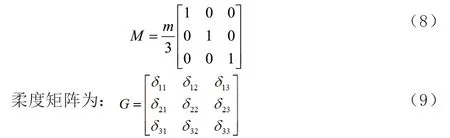
其中，為柔度影響系數(shù)，其物理意義為在j坐標施加單位廣義力時沿i坐標所產(chǎn)生的位移。柔度矩陣對角線元素根據(jù)上述單自由度系統(tǒng)中柔度的求解方法計算，對角線之外的元素采用附加力法，利用卡氏定理求解。

將式（8）和式（9）代入式（6），則有：

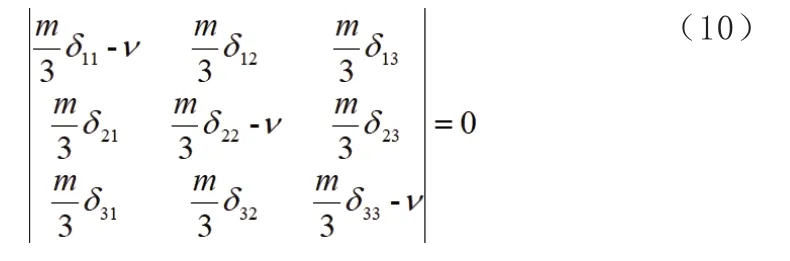
展開后可得ν的三次特征方程，求解該方程可得系統(tǒng)的前三階固有頻率。經(jīng)計算該簡化模型下轉子結構的一階固有角頻率為

3.2 傳遞矩陣法在轉子振動特性分析中的應用

傳遞矩陣法適宜計算鏈狀結構的固有頻率及主振型，像連續(xù)梁、汽輪機、電機轉軸等結構可以簡化為無質量的梁上帶有若干集中質量的振動系統(tǒng)。傳遞矩陣法的基本思路是將離散鏈狀結構系統(tǒng)視為由一系列代表慣性的點和代表彈性的場構成，每個單元上的點傳遞矩陣和場傳遞矩陣構成單元傳遞矩陣，各個單元傳遞矩陣依次連乘構成總傳遞矩陣，最后根據(jù)邊界條件建立頻率方程，求解固有頻率。類似集中質量法，將轉子結構離散成為無質量的變截面梁上帶有若干集中質量的橫向振動系統(tǒng)，由此將連續(xù)問題轉化為多自由度問題。

對于轉子結構的橫向振動問題，任一截面的狀態(tài)向量包括4 個元素，即廣義位移y與θ及廣義力Q與M。

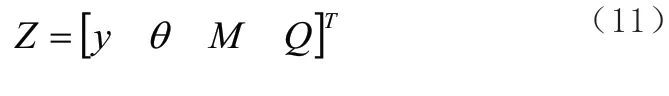
相鄰的狀態(tài)向量之間的傳遞關系為：

Hi為第i個單元的傳遞矩陣，此種離散方式下Hi的表達式為：

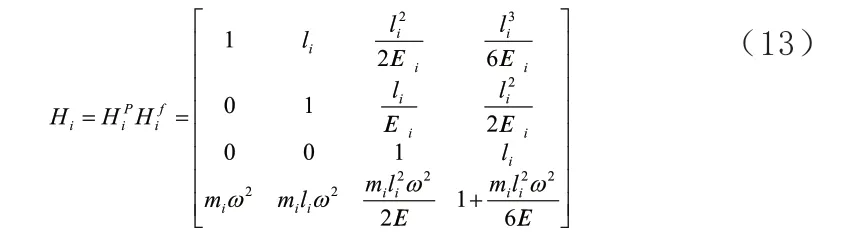
從最左端到最右端的整體傳遞關系為：

H為總傳遞矩陣，其表達式為：

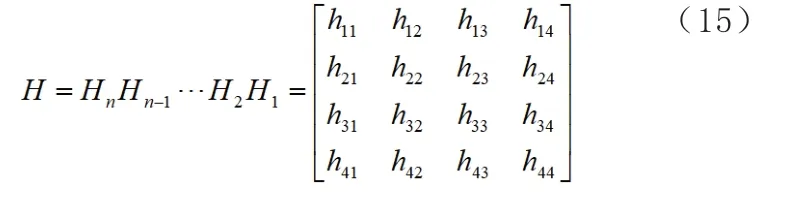
本文分析模型為簡支結構，邊界條件如下：

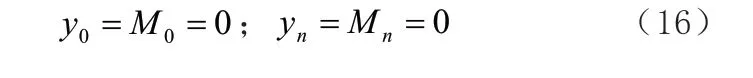
利用式（15）和式（16）導出頻率方程式如下

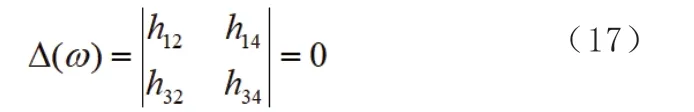
在本示例分析中根據(jù)轉軸的截面分布和質量分布將計算模型劃分為12 個單元，利用數(shù)學計算軟件求得一階固有角頻率為

4 振動特性分析方法的對比研究

通過以上分析方法和計算結果對比研究，將轉動機械結構簡化為單自由度系統(tǒng)最為方便，且能保證一定精度，由于將轉動結構的質量全部集中在轉軸剛度最小區(qū)域，計算的固有頻率小于轉動系統(tǒng)的實際一階固有頻率，對于轉速低于一階臨界轉速的轉動機械結構設計，采用此方法能方便地給出保守的結論，具有重要的實際意義。集中質量法的計算精度與離散密度和質量分配有關，本文示例計算為便于說明情況將質量均勻分配在三個質量點，外側兩個離散質量點離重心較遠，因此計算一階固有頻率可能大于實際固有頻率，當離散密度較高時，計算工作量會隨著自由度增大顯著增加。傳遞矩陣法是將轉動結構系統(tǒng)的計算分解為階數(shù)較低的各單元的計算，每個單元的傳遞矩陣的階數(shù)與系統(tǒng)的自由度無關，從而極大的減少了構造矩陣的計算工作量。目前有限元法在工程應用中最為廣泛，對于復雜模型的分析一般采用有限元軟件進行仿真計算，但理論近似計算分析更容易使設計人員認識和掌握轉動機械結構振動特性分析的理論內(nèi)涵，從而更好的指導設計工作。

5 結語

我國正在從制造大國到制造強國轉變，制造業(yè)正在向高質量發(fā)展，要實現(xiàn)這樣的目標需要各個崗位上的工作者共同努力。對于機械設計人員需要不斷夯實基礎理論，拓展專業(yè)知識面，在中高速轉動機械結構設計過程中，準確的振動特性分析非常重要，可以保證在合理的結構下有效避免機械運行中發(fā)生共振的可能，設計人員需要掌握振動特性分析方法，理解分析方法的理論內(nèi)涵，合理簡化分析模型。