三角網格曲面共形參數化研究綜述

李海生，曹國梁，魏 陽，吳曉群，蔡 強

(1.北京工商大學計算機學院，北京 100048；2.食品安全大數據技術北京市重點實驗室，北京 100048)

隨著3D 采集技術的日趨成熟，大量三維模型數據被應用于各個領域，其復雜的幾何外形，使得三維曲面表面網格處理成為一項艱巨的任務。以紋理映射為發端，曲面參數化[1-2]逐漸成熟起來，通過建立三維曲面到特定參數域的映射關系，把三維網格參數化到參數域空間，并對參數化后的網格進行處理，為復雜曲面的處理提供了新的角度。

參數化探討的是：給定一個由空間點集xi∈R3組成的三角網格曲面S和一個參數域D，尋求一個在參數域上的點ui∈D到xi∈S的一一映射ψ，使得參數域上的網格與原始網格拓撲同構，并在保證參數域上所有三角網格之間不相互重疊的同時，尋求與原始網格之間幾何度量的變形最小化，即畸變最小化。本文討論的所有曲面都是黎曼曲面，即連通的一維復流形。

根據參數化特點的不同，主要分為等距、保面積[3]和保角參數化。保角參數化在變換前后保持曲面三角網格夾角不變的同時保持了曲面的局部形狀，所以又稱為共形參數化，能夠對任意拓撲曲面進行參數化。

用S和S*分別表示源曲面和目標曲面，φ:S→S*表示映射。令(x,y,z)表示源曲面局部坐標，(u,v)表示目標曲面的局部坐標，映射的局部表示為

假設φ:S→S*是微分同胚，γ1,γ2S? 是原曲面上曲線，相交于點p＝γ1∩γ2，如圖1 所示。在交點p處，曲線的切向量交角為θ。φ曲線γ1,γ2映射成目標曲面上的曲線φ（γ1）,φ（γ2），相交于φ（p），并且曲線φ（γ1）,φ（γ2）在φ（p）處的交角也等于θ，即

圖1 保角變換示意圖 Fig.1 Diagram of conformal transformation

如果上式對應一切可能的曲線γ1,γ2均成立，則映射φ被稱為保角變換，也稱共形變換。由于計算機處理離散曲面，很難滿足完全保角的情況，所以共形性也常常被稱作最大相似性(similarity)。

對于共形參數化而言，結合不同參數域的選擇，往往能夠確定參數域的邊界以及函數求解方法。本文主要以參數域作為分類依據，綜述了近年來基于三角網格曲面的共形參數化方法，對現有的參數化算法進行優缺點比較，并討論了共形參數化目前存在的主要難點問題和今后可能的發展趨勢。

1 相關概念

曲面共形參數化方法不僅利用拓撲性質，還依賴于各類離散理論對網格進行度量。如，微分1 形式、同倫群基底、圓填充理論等。下面簡要介紹幾類廣泛應用于共形參數化的相關概念與理論基礎。

1.1 調和映射

如果曲面有類似圓盤一樣的拓撲結構，即曲面是帶有邊界的單連通曲面，那么調和映射[3]就能解決共形參數化的問題。黎曼流形間的調和映射是學習幾何和拓撲的重要工具。調和映射的數學本質是求解一個橢圓偏微分方程，這使得計算能夠有效進行并得到穩定的數值解。目前調和映射最常見的就是采用離散拉普拉斯-貝爾特拉米(Laplace-Beltrami，LB)算子[4]，LB 算子是Laplace 算子在流形上的推廣。如果有頂點數為n的三角網格M，f是定義在M上的函數，則該函數在頂點vi處的離散LB 算子為

其中，ωij為作用在邊ij上的權重，根據ωij取值的不同，調和映射的結果也不同。調和映射的思想就是尋找合適的能量函數，通過對函數優化從而使得調和能量最小。特別的對于零虧格閉合曲面，在自由邊界的前提下調和映射和共形映射等價。

1.2 擬共形映射

擬共形參數化和共形參數化不同之處在于共形參數化將曲面上無窮小圓映射成無窮小圓，而擬共形參數化則將曲面上無窮小圓映射成無窮小橢圓，曲面的局部形狀不能被完好保持。但是對于找不到共形參數化方法的曲面而言，擬共形映射也是很好的補充。

1.3 離散曲率流

曲率流，顧名思義，就是讓曲率像熱流一樣進行擴散。通過將曲面黎曼度量形變，使得曲面的曲率依隨時間而演化，最后曲率趨于一個常數，從而將三維曲面展平到二維參數域，即尋找一個合適的能量函數，使曲率流能得到唯一的最優解。

1.4 同倫群基底

通常對于較為復雜帶虧格三角網格曲面的參數化需要先求曲面的一個切割圖，使得曲面在切割之后拓撲上等價于圓盤。其切割圖中每個度不等于2 的節點將切割圖分成一系列分支{a1,b1,a2,b2,…,ag,bg}，這些分支就是基本群的生成元，也叫基本群的基底。假設有一個曲面S，q∈S是在S上的基點，這里的基點是指滿足有理參數曲面張量積為零的參數對，g為曲面虧格數。在曲面S上，從q出發最終又回到q而沒有交叉點的線路組成了通過q的回路。如果任意2 條通過q點的回路l和l?可以在不離開曲面S的情況下從一條回路連續地變換成另外一條，稱這2 條回路彼此同倫，所有同倫回路構成同倫類。所有同倫類形成同倫群表示為π1(S,q)。π1(S,q)的一組生成元由{a1,b1,…,ag,bg}組成。圖2(a)表示同倫群π1(S,q)其中的一組生成元{a1,b1,a2,b2}，圖2(b)顯示了S的一個基本域，其邊界表示為龐加萊給出了二維曲面拓撲同胚的前提，即當且僅當其的基本群同構。因此可以通過計算曲面的同倫群基底將帶虧格曲面映射到基本域。

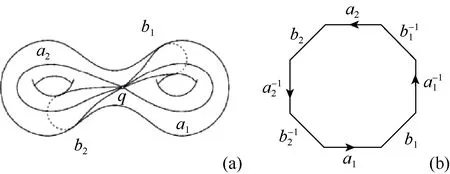
圖2 基本群的典范基底及其基本域 ((a)通倫群基底；(b)基本域) Fig.2 A set of canonical basis of the fundamental group ((a) Homotopy group basis;(b) Fundamental domain)

1.5 圓填充理論

圓填充(circle packing，CP)就是在離散情形下，通過CP方法[5]的引入在網格的每個頂點處設置一個圓，圓的半徑即為網格的度量。在不同幾何背景中，在共形形變保證圓與圓交角不變的情況下，通過改變半徑，達到參數化的目的，如圖3所示。在網格上，頂點的曲率一般和網格邊長相關，而CP 理論成功地建立了曲率與網格頂點的關聯，這樣通過改變在頂點上圓的半徑就能使曲率跟隨變化。

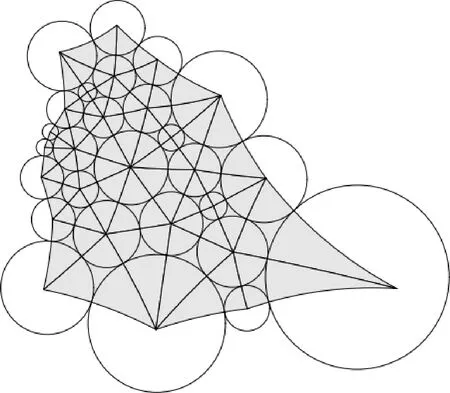
圖3 圓填充示意圖 Fig.3 Diagram of circle packing

1.6 離散Ricci 流

Hamilton 定義了關于高斯曲率的Ricci 流[6]，即

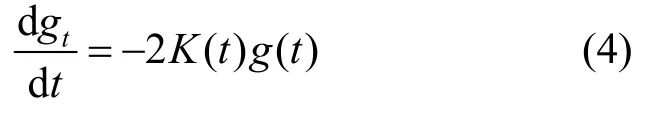
其中，g(t)為與時間相關的度量；K(t)為隨時間而變化的高斯曲率。將其推廣到離散情形，即

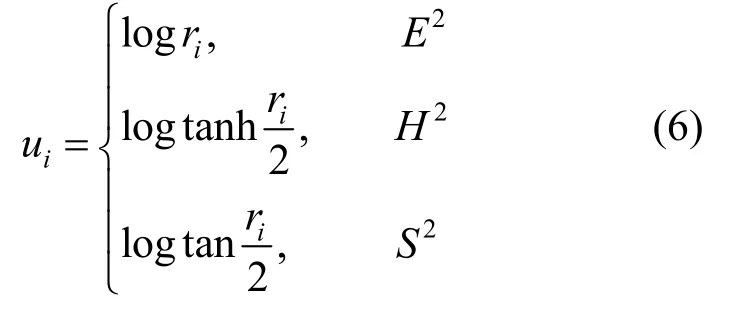
離散曲率流通常采用CP 度量作為網格初始度量，在得到邊長后利用余弦定理計算出網格中每個三角形{vi,vj,vk}的內角角度θi,θj,θk，以θi計算為例，即

其中，θi為在三角形{vi,vj,vk}中以vi為頂點的角；li為頂點vi對應的邊ljk的邊長，不同嵌入背景下角度余弦定理的計算不同。由此可以計算出網格上每個點vi的離散高斯曲率

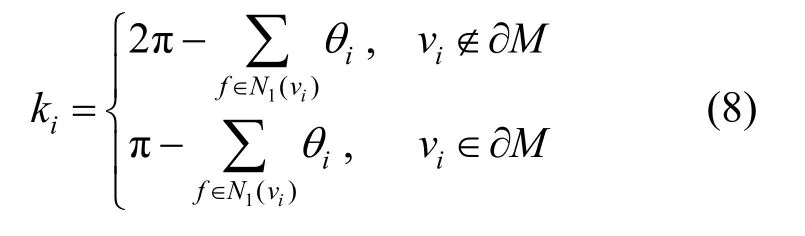
離散高斯曲率被定義為角欠(angle deficit)，對于內頂點，角欠就是圍繞頂點的周角與2π作差，對于邊界頂點，則與π作差，角欠在一定程度上反映了曲面局部的凹凸變化。

2 參數域

參數化的應用決定了參數化的首要步驟就是確定一個合適的參數空間。根據曲面拓撲結構的不同，幾何背景通常是歐氏平面、單位球面和二維雙曲空間中的一種。根據不同的幾何背景，參數化的參數域選擇往往不同。根據參數域的不同，把共形參數化分為平面域、球面域和雙曲空間域3 類(圖4)。

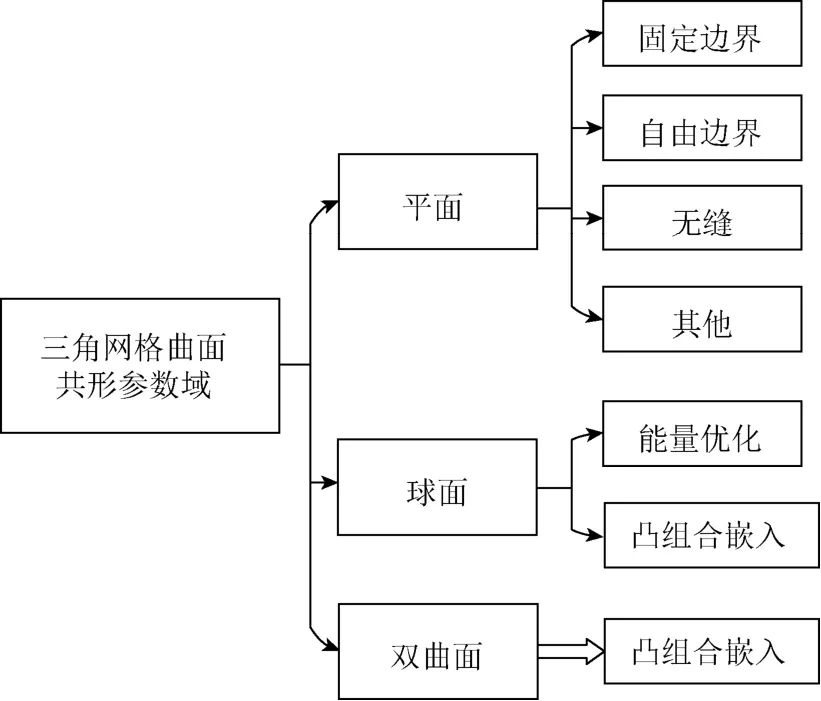
圖4 參數域分類示意圖 Fig.4 Diagram of parameter domain classification

3 平面域

對于共形參數化而言，參數域通常是平面域，平面也是歐式空間中最常見的二維表示。平面參數化最早主要用來進行3D 紋理貼圖，對于紋理和圖像而言，平面是最自然的載體，對平面圖像的處理復雜度遠小于直接操作三維曲面。從應用的角度最為常見的平面域就是固定邊界，但在參數化的過程中可能導致邊界網格變形嚴重，為了解決邊界參數化失真的情況，自由邊界參數化和無縫參數化得到發展，但是推廣到復雜拓撲曲面的情形，這2 類參數化往往效果不佳。

針對平面域，主要有以下幾類常見共形參數化方法。

3.1 固定邊界參數化

早期的平面參數化方法大多將原始網格映射到平面凸多邊形上，即首先找到原始網格的邊界，并將邊界點映射到平面凸多邊形上，然后將每個內部點表示為其一環點的加權平均，最后通過求解線性方程組得到相應的參數化結果。其中有代表性的是TUTTE[7]的凸組合嵌入；文獻[3]最早介紹的離散調和映射；還有FLOATER[8-9]的保形參數化和基于調和函數中值定理提出的均值(mean-value)參數化方法，以上方法的區別在于使用了不同的加權方法。

對于帶有多邊界的聯通曲面，共形幾何理論[10]保證其能被共形映射到平面圓域上，平面圓域的好處在于無論邊界點個數多少，總能保證參數域邊界光滑，以確保視覺效果良好。此外，圓域中心和半徑都是由曲面的幾何決定的，其更能保持曲面局部形狀。這類參數化中的經典當屬Koebe 迭代方法[11]，如圖5 所示，文獻[12]提出廣義Koebe 迭代方法，即對傳統Koebe方法中圓盤映射

圖5 傳統Koebe 迭代方法[11] ((a)多邊界曲面；(b)首次共形映射；(c)第二條外圓邊界；(d)內部區域填色；(e)第二次共形映射) Fig.5 Conventional Koebe’s iteration method[11] ((a) Multi-boundary surface;(b) First mapping;(c) The second boundary; (d) Filling color;(e) Second mapping)

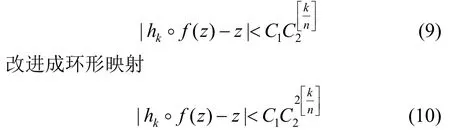
每次選擇2 個邊界映射成環，保留Koebe 迭代線性高效的同時，加快了函數收斂速率，提高了計算效率。

對于零虧格曲面，GU 和YAU[13]提出一種非線性優化方法來計算零虧格曲面的全局共形參數化，該方法對球的切平面進行優化，不足之處為算法梯度下降過程慢，并且處理細長特征時容易產生網格重疊的現象。在此基礎上，CHOI 和LUI[14]優化了共形結果，提出了一種針對圓盤拓撲曲面的線性參數化方法，如圖6 所示。通過求解稀疏對稱正定線性方程組，結合擬共形映射減小共形扭曲以確保函數雙射，能夠處理尖銳且不規則的三角網格，提高了計算效率。但該方法目前還不能最優分配邊界頂點，這樣效果會受到影響。

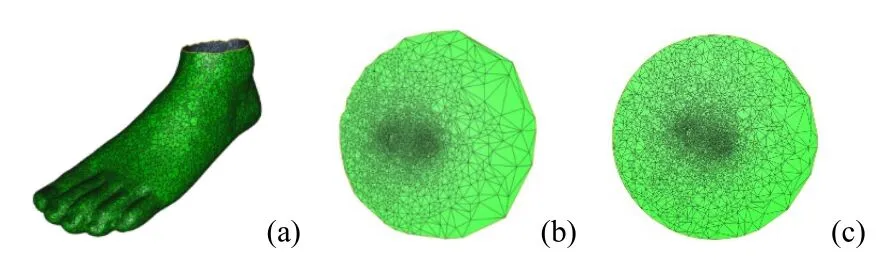
圖6 圓盤線性參數化[14] ((a)輸入模型；(b)雙重覆蓋；(c) Choi 改進) Fig.6 Linear parameterization of disk topology[14] ((a) Input model;(b) Double covering;(c) Choi’s improvement)

對于單虧格曲面的共形參數化，常常使用微分1 形式和曲率流進行計算。不同于曲率流，微分1形式計算一個全純映射，進而給出曲面的一種度量，共形于原度量。文獻[15]中實現了單虧格曲面共形結構的計算，該方法基于Hodge 理論[16]，通過將全純1 形式與虧格相關的奇點數相結合來獲得給定曲面的平坦度量。算法首先計算網格曲面的同倫群基

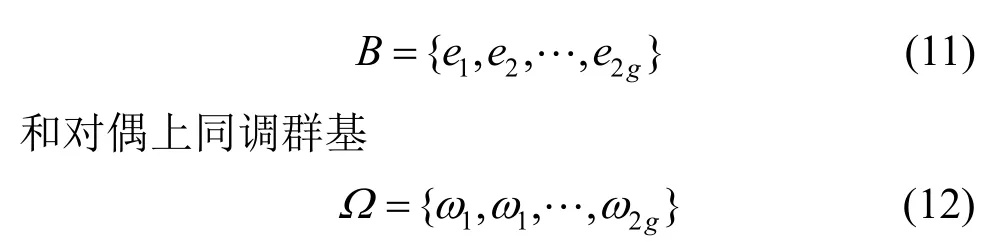
并對每個ωi計算與之上同調的唯一的調和1 形式ζi，接著計算每個ζi的共軛，記為*ζi，從而構造全純1 形式

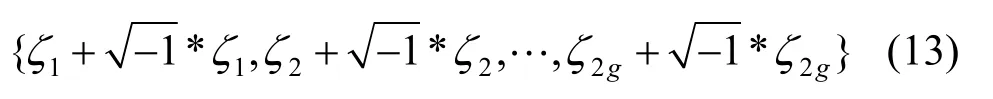
對以上全純微分基形式進行求積分，便能得到對應的共形映射。該方法可找到一個全純1 形式的完備基。

LUO[17]研究了曲面上的離散Yamabe 流，并將其作為微分1 形式的積分對曲面上的度量進行共形變化，通過使用余切拉普拉斯方程將曲率進行熱流擴散。LIU 等[18]提出了基于歐式Ricci 流的曲面共形參數化方法，通過設計邊界曲率來控制邊界點的位置。隨后文獻[19]通過將全純1 形式與虧格相關的奇點數相結合來獲得給定表面的平坦度量，利用牛頓 迭代法不斷優化能量函數通過創建離散Ricci 邊權重矩陣(Hessian 矩陣)來更新共形因子，達到更新圓填充度量的效果，從而獲得全局平滑的參數化。基于微分1 形式的方法雖然高效，但是對于高虧格曲面的計算，往往會產生不必要的奇異點，導致整體參數化質量下降。

對于高虧格曲面，文獻[20]提出一種基于調和映射的非線性參數化方法。該方法首先采用貪心算法找到高虧格曲面的同倫群基底，沿基底將曲面切開以簡化其拓撲，然后通過余切邊權重計算曲面的調和映射，最后使用拉普拉斯切向法最小化調和能量得到共形映射。和曲率流方法不同之處在于，該方法簡單易行，并且使用的平面度量也方便用于曲面擬合，不需要高質量的三角網格使該算法魯棒性更強，不足之處在于未涉及高精度模型的處理，即高質量三角化模型特征保留的問題。

這類固定邊界參數化方法的優勢在于用到的變形度量都是線性函數，缺點在于這些算法通常預先指定邊界在某個凸多邊形上，由于預先指定的邊界與實際情況往往不相符，從而導致參數化前后變形較大[21]。

3.2 自由邊界參數化

固定邊界的參數化算法易于構造函數并求解，但是容易導致邊界網格扭曲嚴重，且不易推廣到復雜外形的曲面。相比之下，另一類平面參數化算法[22-31]把邊界作為求解的一環，不固定邊界的形狀從而減小失真。這類參數化方法也稱為自由邊界參數化，其使得平面參數化的理論更加完備。

文獻[22]提出了最小二乘共形映射(least squares conformal maps，LSCM)，采用最小二乘近似柯西-黎曼方程的方法計算了圓盤拓撲曲面的擬共形參數化。文獻[23]介紹了一種基于角度平展(angle based flattening，ABF)的非線性參數化方法，把參數化過程建模為一個求解角度的模型，在得到二維平面上模型中每個三角形的3 個角度之后，再根據角度間接求解頂點的位置，缺陷在于存在邊界自交問題，并且計算代價較高。隨后文獻[24]改進了ABF 提出的ABF++方法，其將三角網格曲面的參數化問題表述為參數網格角度誤差的最小優化方程，即

進行線性近似

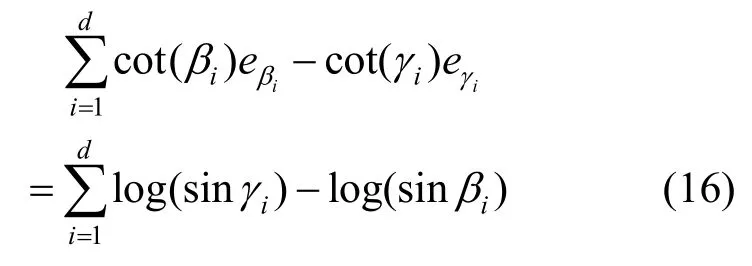
在提高計算效率的同時減少了角度誤差，缺陷是增大了面積變形。圖7 為ABF++方法和線性ABF方法變形程度比較，可以看到，這類方法直接對角度進行優化以達到保角的效果，線性ABF方法更注重角度和面積變形的均衡。

圖7 2 種角度方法比較[25] ((a) ABF++方法；(b) Linear ABF方法) Fig.7 Comparison of two angle methods[25] ((a) ABF++method;(b) Linear ABF method)

文獻[26]設計一種譜方法共形參數化 (spectral conformal parameterization，SCP)方法來尋找稀疏對稱矩陣的特征值，通過最小化加權共形能量來計算高質量共形參數化，相比之前的線性方法[27]，該方法計算速度不占優，且不能保證生成無折疊(fold-free)的參數化結果，但優點在于共形扭曲更小；和一些非線性方法[28]相比，該方法速度一般，但參數化結果視覺效果更好，尋求計算開銷與參數化質量之間的一種均衡。文獻[29]設計了一種自由邊界曲率擴散的算法，該方法使用CP 度量簡化共形映射，從初始的共形參數化開始，優化面積扭曲函數，同時保持CP 度量共形等價，最后通過反曲率映射得到最優共形參數化，該方法控制了面積變形，但只優化了奇異頂點，仍需改進的是對整個頂點集的優化。

文獻[33]對SCP，ABF++和剛性變換[31](as rigid as possible，ARAP)方法進行了介紹，同時提出一種滿足雙射條件的非線性自由邊界參數化，即自由邊界雙射映射(bijective parameterization with free boundary，BPFB)方法，但該方法不屬于共形參數化方法。圖8 和表1 分別給出了SCP，BPFB 等 4 種方法的結果比較。可以看到，相比于其他自由邊界參數化方法，ABF++方法的求解效率較高，且參數化后扭曲較小。

圖8 自由邊界參數化效果比較[33] Fig.8 Comparison of free boundary parameterization quality[33]

表1 自由邊界參數化算法計算速度比較[24] (s)Table 1 Comparison of calculation speed of free boundary parameterization algorithms[24] (s)

3.3 無縫參數化

不論是固定邊界還是自由邊界，平面參數化都針對拓撲等價于圓盤的曲面。由于構造拓撲圓盤的過程中，往往需要對曲面進行切割，對于切割處的參數化容易產生誤差。因此，近年來對于無縫曲面參數化的研究日益增多，無縫參數化常被用來進行無縫紋理映射[34]和形狀匹配[35]。無縫參數化直觀解釋就是沒有產生切割偏差的參數化，在切割過程中采用剛性變換進行過渡。例如MYLES 和ZORIN[36]面向無縫全局參數化，提出一種增量平展方法，將錐形奇異點即錐點(cone singularities)放置在網格表面上，從嵌入度量開始迭代表面的度量，將表面不斷增長的部分限制為零高斯曲率，高斯曲率將集中在孤立的收縮區域，最終形成錐點。AIGERMAN等[37]設計了一種無縫映射的方法，如圖9 所示，該方法首先對曲面進行切割，然后分別映射到平面進行比較，對不重合的區域進行一系列仿射變換，通過最小化共形扭曲能量函數得到曲面的無縫參數化。該方法能處理任意數量的標記點(landmarks)，缺陷在于非線性求解保證找到函數局部最優解，但計算代價高。

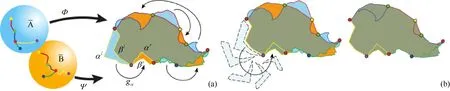
圖9 無縫映射示意圖[37] ((a)分別參數化到平面；(b)非重疊部分進行仿射變換并得到參數化結果)Fig.9 Diagram of seamless mapping[37] ((a) Mapping to a disk respectively; (b) Affine transformation of non-overlapping parts and result)

文獻[38]將凸組合嵌入方法應用在歐式軌道流形(euclidean orbifold)上，通過求解稀疏線性系統來計算嵌入，該方法能夠生成無縫的全局參數化，且滿足曲面到歐式軌道流形之間的雙射，不足之處在于只能放置有限錐點，因而不能進一步減小參數化導致的扭曲。

3.4 其他參數化

和上述平面參數化方法相比較，SPRINGBORN等[39]提出三角網格共形等價(conformal equivalence of triangle meshes，CETM)通過最小化凸能量函數將表面網格映射到平面域，并設計自動放置算法減少參數化的失真，從而構造離散共形等價。文獻[40]提出一種線性參數化方法邊界優先映射(boundary first flatting，BFF)。不同于自由邊界和固定邊界的方法，BFF 通過稀疏矩陣分解能夠直接、完全控制邊界長度和角度，即意味著邊界可以手動編輯，且有成型的軟件供用戶使用。相比于傳統的共形參數化方法LSCM[22]和SCP[26]，BFF 能夠適應任意邊界條件，相比于CETM 等非線性方法，BFF 計算代價更小，且參數化效果幾乎相同，如圖10 所示。

圖10 BFF方法和CETM方法比較[40] ((a)原始模型；(b) CETM方法；(c) BFF方法) Fig.10 Comparison of BFF method and CETM method[40] ((a) Input model;(b) CETM method;(c) BFF method)

相比于無縫參數化，BFF方法能針對任意錐點放置的參數化，使參數化適應尖銳的拐角，從而將曲面共形參數化到任意形狀。BFF方法的不足之處在于只能處理拓撲于圓盤的曲面。進一步，文獻[41]在不超過固定總錐角的所有可能的錐度配置情況下將全局失真最小化。

通過對目前比較流行的平面參數化方法進行匯總，總結出相關的參數化方法、參數域邊界條件、是否滿足雙射以及方法是否迭代，見表2。

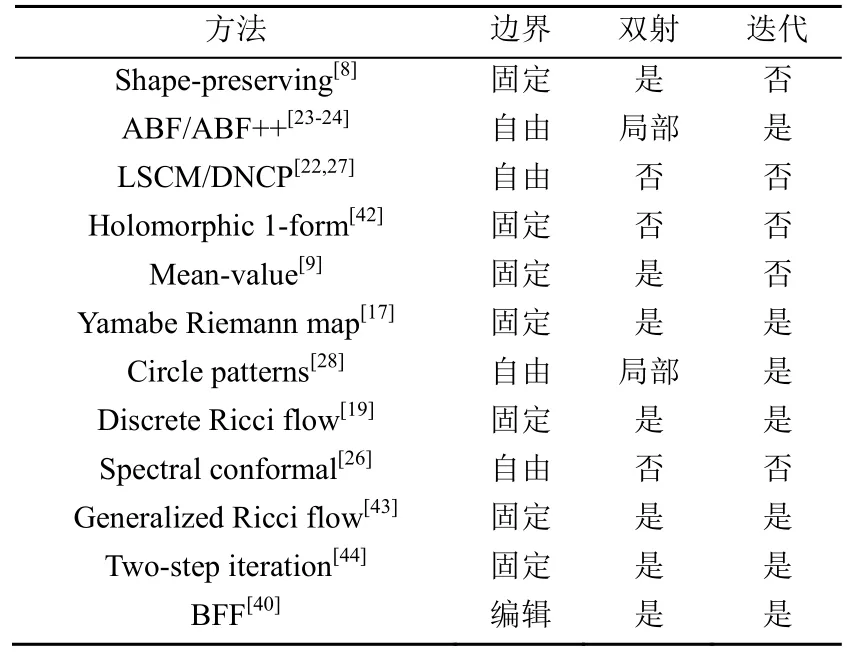
表2 平面參數化方法匯總Table 2 Summary of planar parameterization methods

4 球面域

除了平面參數化，另一種常見的參數域就是單位球面，將三維曲面參數化到球面上。假設有角度θ∈[0,2π)，?∈[-π/2,π/2)，則球面坐標為

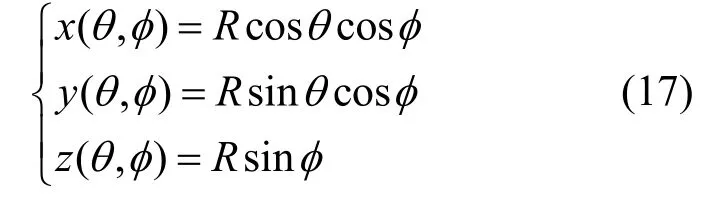
如圖11 所示，對于每對θ和?的取值，都能對應球面上一個點坐標。

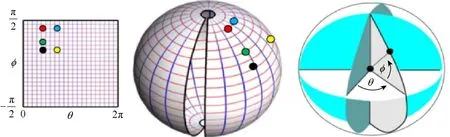
圖11 球面坐標系示意圖 Fig.11 Diagram of spherical coordinate

由于零虧格曲面在拓撲上等價于單位球面，因此對于零虧格曲面而言，球面域是天然且無縫的參數域。根據求解方法的不同，球面共形參數化主要分為基于能量優化的方法和基于凸組合嵌入的方法。

4.1 基于能量優化方法

該方法主要思想是構造不同的能量函數，通過對能量函數進行優化從而將源曲面參數化到單位球面。GU 等[45]指出，虧格為0 的閉合曲面的共形映射可以由球面間調和映射來實現。LAI 等[46]通過最小化調和能量來進行球面參數化，該方法對于狹長的網格能產生無折疊的參數化，效率和效果在以往參數化[13]基礎上有提升，但沒有推廣到任意拓撲曲面。WANG 等[47]提出ARAP 的球面參數化方法，通過對球半徑迭代優化解決球面參數化過程中存在的非線性約束問題，從而將平面ARAP[31]方法推廣到球面域。隨后在文獻[48]中提出一種低失真雙射映射(bijective and low distortion，BLD)方法，該方法在球面ARAP方法基礎上采用一種塊坐標下降的迭代算法進一步減小失真，并保證了參數化雙射。圖12 為4 種典型球面參數化方法的比較，其中深色部分代表三角網格失真嚴重或出現翻折的情況，參數化結果下方對應的4 個數值分別表示最大失真、平均失真、超出BLD方法最大失真三角面片數目以及超出BLD方法倒置的三角面片數目。

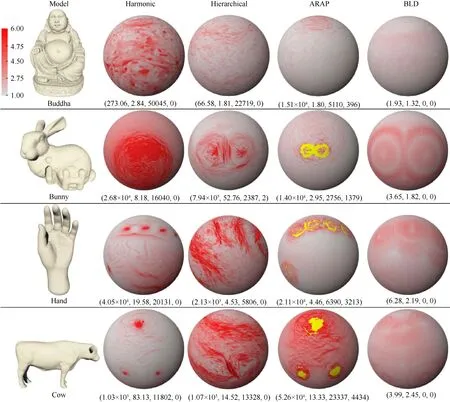
圖12 4 種球面參數化方法效果對比[48] Fig.12 Comparison of the effects of four spherical parameterization methods[48]

4.2 基于凸組合嵌入方法

該方法可將平面凸組合的方法推廣到球面域，即把網格嵌入球面凸多邊形，在保留凸組合方法求解簡單高效的同時，和球面域的天然特性進行結合，以產生高質量的參數化。AIGERMAN 等[49]將凸組合嵌入的方法擴展到了球形目標域，參數化滿足雙射條件并且計算速度較快。相比于歐式情形[37]，該方法等價于共形映射，參數化失真小，球面的錐點放置靈活，不足之處在于該方法必須預先指定錐點的位置及角度，并且該方法有2 個假設不能保證總是成立，只有滿足這2 個假設才能得到相應參數化結果，即：假設球面最大邊長不超過π/2；假設排除了迪利克雷(Dirichlet)能量的關鍵點，這些關鍵點屬于非平凡的同倫類。

5 雙曲空間域

除了平面域和球面域，雙曲空間域也是共形參數化的研究重點。雖然不及平面域的簡易性(易于構造，求解快速)和球面域的天然性(零虧格曲面拓撲等價，曲率恒正)，但是雙曲空間域能夠處理更多錐點的放置情況，并且對于復雜拓撲曲面，即高虧格曲面而言，雙曲結構有潛力取代定義在流形樣條中的仿射結構，這也使得目前對于高虧格曲面的處理，大多選擇雙曲平面作為參數域。

AIGERMAN 和LIPMAN[50]將凸組合嵌入方法推廣到了雙曲空間，滿足映射無縫同胚的同時具備處理高虧格曲面的能力，和其他處理高虧格曲面不同的地方在于切割的方法。雙曲空間凸組合嵌入的方法缺陷在于固定參數域的邊界會影響參數化的質量，并且切割的方式比較簡單，錐點手動放置生成，不能保證最優選擇。圖13 給出3 種典型參數空間下凸組合嵌入的效果圖。

圖13 不同幾何背景下的凸組合嵌入效果圖比較[38,48-49] ((a)歐式平面；(b)雙曲平面；(c)球面) Fig.13 Comparison of convex combination embedding effects in different parameter spaces[38,48-49] ((a) Euclidean plane;(b) Hyperbolic plane;(c) Spherical plane)

6 總結與展望

經過多年的發展，參數化已經成為幾何模型處理中的關鍵一環，而共形參數化又以參數化前后保角和保形的特性備受青睞。本文對三角網格曲面共形參數化進行了綜述，從方法角度根據不同的目標參數域進行分類，對每一類共形參數化方法進行歸納總結：

(1) 平面參數化。平面參數化是最為常用的參數化方法。其中固定邊界方法的優勢在于用到的變形度量計算效率較高，缺點在于預先指定邊界會導致參數化前后變形較大；自由邊界方法改善了固定邊界的失真，適用性大幅提高；無縫參數化克服參數化的預處理從而沒有產生切割偏差；其他參數化更多的體現在對邊界的可控。

(2) 球面參數化。對于零虧格曲面而言，球面參數化可以達到天然且無縫的效果。能量優化的特點在于控制迭代次數從而實現不同參數化效果；凸組合嵌入實現雙射，得到高質量映射結果。

(3) 雙曲空間參數化。高虧格曲面大多應用雙曲空間參數化方法。

但是現階段仍然有一些問題束縛著共形參數化的發展，例如，對于復雜拓撲曲面需要將大量精力放在尋求割線的處理上面，不同的處理方式對后期的參數化效果有較大影響。

參數化在過去核心價值在于轉化三維空間中不易直接處理的操作，而共形的意義在于通過保持參數化過程角度損失最小從而減小變形帶來的幾何誤差。三維的三角網格曲面通過共形參數化能夠實現3 類參數域的全局表示，選用合適的雙射算法，能夠實現幾何處理的自動化和智能化。

隨著計算機軟硬件的發展和人工智能的崛起，有學者嘗試著從幾何角度去理解深度學習[51]，通過共形參數化前后幾何結構保持不變，可以簡化幾何深度學習的輸入，此外這方面研究也可能揭示數據分布與共形幾何間的內在關系。