基于深度估計和特征融合的尺度自適應目標跟蹤算法

牟 琦，張 寒，何志強，李占利

(1.西安科技大學計算機科學與技術學院，陜西 西安 710054；2.西安科技大學機械工程學院，陜西 西安 710054)

視覺目標跟蹤是指根據給定的第1 幀圖像中目標的狀態，對后續視頻幀序列中目標的位置進行估計的過程，被廣泛應用到視頻監控、智能機器人和人機交互等領域[1-3]。基于相關濾波的目標跟蹤方法由于跟蹤效率高、精度好等優點被廣泛關注，在其基礎上改進的目標跟蹤算法在跟蹤領域占據主導位置[4-7]。

BOLME 等[8]提出的誤差最小平方和濾波器(minimum output sum of squared error filter，MOSSE)算法，將相關濾波應用到跟蹤領域，通過傅里葉變換把濾波運算轉到頻域，大幅提高了目標跟蹤算法的效率。HENRIQUES 等[9]提出的核循環結構(circulant structure with kernels，CSK)算法將循環矩陣的理論和核方法應用到相關濾波跟蹤中，優化目標跟蹤算法的運動模型和觀測模型，實現了對目標移動更為魯棒的相關濾波目標跟蹤算法。HENRIQUES 等[10]將多通道的方向梯度直方圖(histogram of oriented gradient，HOG)特征與CSK框架結合，提出了核相關濾波目標跟蹤算法(kernelized correlation filters，KCF)，該算法提取目標的HOG 特征對目標建模，大幅提升了相關濾波目標跟蹤的準確度。

以上基于相關濾波的目標跟蹤算法在簡單環境且目標尺度未發生明顯變化時，能夠快速跟蹤目標，得到良好的跟蹤效果。但在實際場景中，目標背景通常比較復雜，且目標尺度可能發生較大變化。KCF 算法使用單一特征訓練跟蹤模板，無法充分地表示目標特征，在復雜場景中魯棒性低，易受環境的影響；另外，當目標與鏡頭距離發生較大變化時，KCF 無法根據目標的變化動態調整跟蹤邊框的尺寸，目標窗口內會存在大量的非目標區域或不能完全包含目標，導致濾波器在后續跟蹤中學習到錯誤特征，所訓練出的跟蹤模板被污染，無法正確地跟蹤目標。針對目標尺度變化問題，文獻[11]提出了基于相關濾波的判別型尺度空間算法(discriminative scale space tracking，DSST)，通過分別構建一個平移濾波器和一個尺度濾波器實現對目標的尺度自適應跟蹤。該算法能對目標尺度進行比較準確地估計，但是當目標尺度變化較大時，算法效率較低。本文針對環境復雜、目標尺度變化而導致跟蹤效果不理想的問題，提出了一種基于深度估計和特征融合的尺度自適應目標跟蹤算法。當目標與鏡頭距離發生較大變化時，目標的深度和尺度會同時發生變化，并且二者之間會存在相關關系。基于以上相關關系，本文算法首先通過深度估計網絡，建立深度-尺度估計模型，估計目標的尺度，從而在目標尺度發生變化后，能夠自適應地調整目標框大小，實現更加魯棒的目標跟蹤。本文算法所采用的左右一致性單目深度估計網絡可以直接對視頻序列圖像估計深度信息，無需深度圖像或雙目圖像序列，因此該算法不受場景和硬件設備的限制，應用場景和經典的相關濾波目標跟蹤算法KCF 相同。

另外，在目標跟蹤中，利用目標的特征建立目標的外觀模型，其直接影響目標跟蹤的精度。因此，使用強有力的特征來描述目標對實現準確的目標跟蹤非常重要。HOG 特征是通過計算和統計圖像局部區域的梯度方向直方圖得到的，在圖像的局部方格單元上操作，受圖像的光照變化和幾何形變影響小，但是對目標的姿態、角度的變化十分敏感。顏色(color name，CN)特征是全局特征，描述整個目標不同顏色通道的數量統計，對目標角度的變化、局部形變不敏感，且包含了豐富的場景信息，有利于區分目標與背景。為了更加充分地描述目標，本文將HOG 特征和CN 特征相融合，對目標外觀建模，有效地提升了模型的表征能力。

本文提出深度-尺度估計模型，利用目標的深度值估計尺度值，實現尺度自適應目標跟蹤。和KCF算法相比，提高了跟蹤的準確度；和DSST 算法相比，在尺度變化較大時，跟蹤速度更快；在環境復雜、目標移動過程中出現與目標顏色近似的遮擋物時，魯棒性更好。

1 相關工作

1.1 相關濾波目標跟蹤算法

相關濾波目標跟蹤算法將信號的相關性理論引入到目標跟蹤算法中，對目標模板與待檢測區域進行相關計算，將響應結果的最大值點作為目標預測中心點。其主要工作就是訓練一個可用于跟蹤的相關濾波模板。目標模板與待檢測區域的相關運算為

其中，f為待檢測區域圖像特征；h為相關濾波模板；g為響應輸出。為了提高運算效率，通常會進行快速傅里葉變換，在頻率域內，將相關計算轉化為點乘運算，即

其中，F為待檢測區域圖像特征經過快速傅里葉變換后的表示；H＊為相關濾波模板經過快速傅里葉變換后的復共軛；G為響應輸出。在跟蹤過程中，通過對待檢測區域進行M次采樣得到F，然后分別構造高斯響應函數得到G，利用最小化均方誤差的方法，訓練得到最優的相關濾波模板，目標函數為

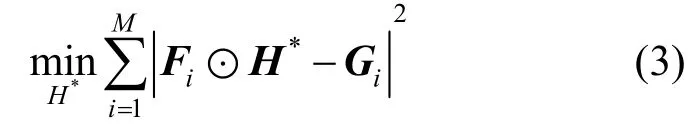
最小化式(3)，得到相關濾波模板的最優解，即

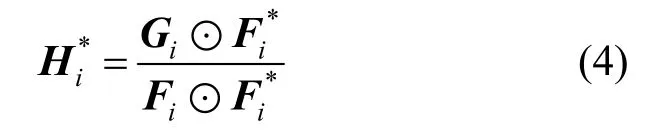
通過式(4)可以求得第i幀圖像中最優的相關濾波模板。為了避免相鄰幀之間目標細微差異對目標跟蹤的影響，將上一幀相關濾波模板與當前幀得到的相關濾波模板加權求和，得到新的相關濾波模板，即

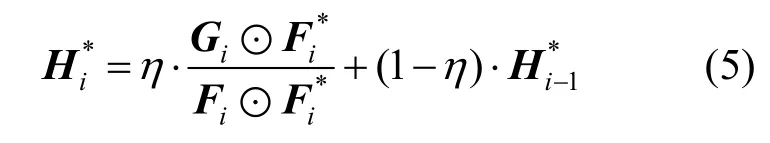
其中，η為學習率，通常取值0.125。

1.2 深度估計網絡

深度圖像中的每一個像素值表示場景中像素點和拍攝點的距離。目前主要是利用激光、結構光等在物體表面的反射獲取場景深度信息，需要較高的成本。深度估計算法通過圖像獲取場景深度信息，無需安裝深度攝像頭，可分為立體視覺方法和單目圖像深度估計方法。立體視覺方法需要至少2個位置相對固定的相機同一時間對同一場景進行拍攝，這一條件限制了其應用范圍。單目圖像深度估計方法只需要一個普通相機，應用場景所受限制更小。

近年來，深度學習在視覺領域表現優異，一些學者開始將深度學習方法應用于目標深度估計問題。

EIGEN 等[12]利用圖像的深度信息作為標簽訓練卷積神經網絡(convolutional neural network,CNN)，實現對圖像深度的估計；此后，在此基礎上出現了一些改進的基于監督學習的方法。但是在某些場景下，無法得到精確的深度信息，因此一些學者轉向研究無監督的深度學習方法。文獻[13]提出了一種基于圖像的單目深度估計網絡。該方法無需用真實的深度信息作為標簽，在訓練時使用相對容易獲取的左右視圖圖像訓練網絡，在測試和應用時僅需要單幅圖像便可得到對應的深度圖。GOARD 等[14]在文獻[13]的基礎上進行優化，進一步提高了無監督深度估計網絡的性能。

圖1 為文獻[14]提出的左右一致性單目深度估計網絡的結構示意圖。

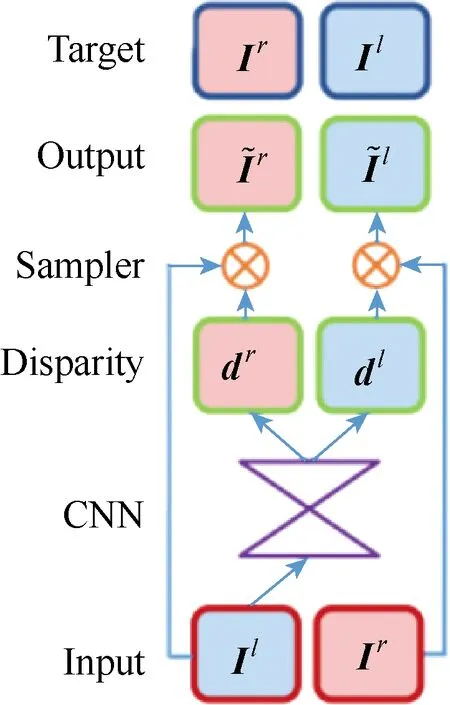
圖1 左右一致性單目深度估計網絡 Fig.1 Monocular depth estimation network with left-right consistency

算法的思想是用重建圖像的方式構建深度估計網絡。訓練階段，網絡的輸入是標定好的雙目相機同步采集的圖像對，左視圖Il，右視圖Ir，通過CNN，得到右視差圖dr和左視差圖dl，分別應用到左視圖Il和右視圖Ir，可以得到重建后的右視圖和左視圖。分別計算重建的左視圖與原左視圖之間的誤差以及重建的右視圖和原右視圖之間的誤差，并引入視差平滑誤差Cds和左右 視差一致誤差Clr，即總誤差C=Cap+Cds+Clr，最小化總誤差C，得到CNN 的各項參數。測試階段，將測試集的左視圖或右視圖輸入到訓練階段得到的CNN，網絡輸出視差d，由雙目相機的成像原理可知：D=Bf/d，其中B為2 個相機之間的距離，f為相機焦距，D為圖像的深度值。

2 本文算法

2.1 主要思想

當目標與鏡頭距離發生較大變化時，目標在空間內的深度信息變化與尺度變化之間存在較強的相關關系，尺度值會隨深度值的增大而減小。根據這種相關關系，本文算法首先根據不同幀中目標深度值和尺度值的變化關系，建立并訓練深度-尺度估計模型，利用該模型對尺度進行估計；然后將得到的尺度值引入到使用特征融合的相關濾波跟蹤算法中，在跟蹤時，自動調整目標邊框尺寸，實現對目標的尺度自適應魯棒跟蹤。

2.2 建立深度-尺度估計模型

本文算法的關鍵是利用訓練數據集建立深度-尺度估計模型，從而通過當前幀目標的深度信息，預測目標尺度值。具體步驟如圖2 所示。

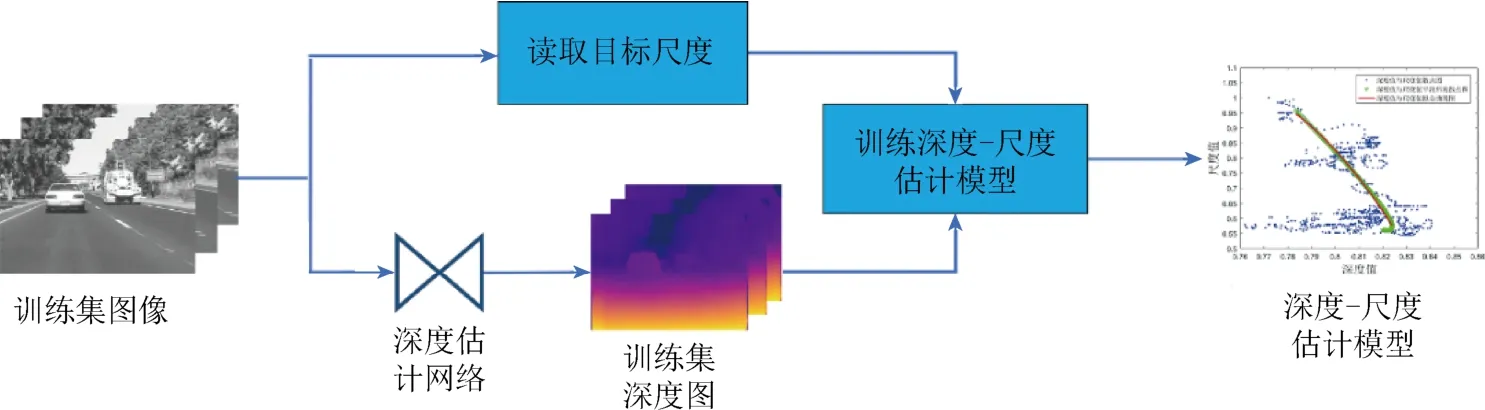
圖2 深度-尺度估計模型 Fig.2 Depth-scale estimation model

主要步驟如下：

步驟1.利用文獻[14]中的左右一致性單目深度估計網絡，得到二維圖像對應的深度圖。

步驟2.提取視頻幀序列中每一幀的目標面積size_i和目標中心位置深度值depth_i，其中i為幀序號，1≤i≤N，N為總幀數。考慮到不同目標的長寬比例不同，本文算法中的尺度采用目標面積來表示。深度值depth_i由步驟1 得到。

步驟3.建立深度-尺度估計模型。隨著目標深度的逐漸增加，尺度逐漸減小，理論上呈線性關系。由于本文算法中的尺度采用目標面積，因此，采用二次多項式來建立深度-尺度模型，即

其中，k1，k2分別為一次項和二次項系數；k0為常數項；scale為目標的估計尺度值。考慮到不同目標面積有較大不同，使用每一幀的面積除以第1 幀面積，作為該幀的真實尺度值trueScale_i，即

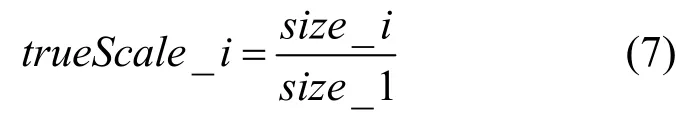
步驟4.訓練深度-尺度估計模型，使用最小均方誤差作為損失函數，即

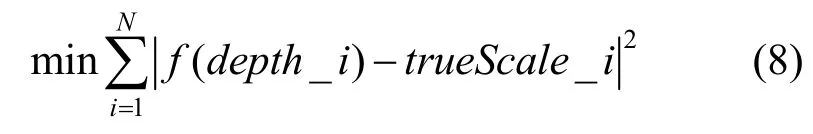
其中，f(depth_i)為第i幀目標的尺度估計值；trueScale_i為訓練數據集中第i幀目標的真實尺度值。

2.3 尺度自適應目標跟蹤

本文提出的尺度自適應目標跟蹤算法如圖3所示。

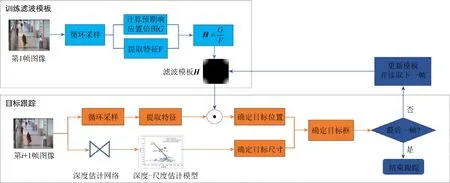
圖3 尺度自適應目標跟蹤算法 Fig.3 Scale-adaptive target tracking algorithm

步驟1.根據視頻序列中第1 幀給定的目標中心點坐標X，在其周圍采樣得到訓練樣本，分別提 取樣本的HOG 特征和CN 特征，2 種特征相加后得到樣本的最終特征F；根據訓練樣本與目標中心點X的距離，生成[0～1]范圍的高斯型標簽，即預期響應置信圖G。使用H=G/F得到相關濾波器模板H。

步驟2.在后續幀中，根據前一幀目標中心點坐標X在當前幀中的位置X'，在X'周圍采樣并提取特征，計算相關濾波器H與樣本特征的響應值，響應值最大處即為目標所在位置。

步驟3.使用深度估計網絡得到目標的深度值depth_i，再利用深度-尺度估計模型得到目標的尺度值S_i，根據得到的尺度值調整目標框尺寸，實現對目標的尺度自適應跟蹤。

為避免深度估計過程中的誤差，本文算法使用第1 幀中目標的真實尺度值對估計尺度值進行矯正，即

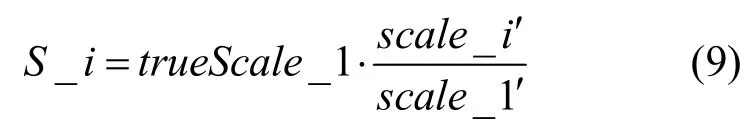
其中，trueScale_1 為第1 幀中目標的真實尺度，scale_1?為通過深度-尺度模型計算出的第1 幀尺度值；scale_i?為通過深度-尺度模型計算出的第i幀尺度值，S_i為矯正后第i幀的估計尺度值。

步驟4.判斷當前幀是否為視頻序列中的最后一幀，若是，則結束跟蹤；否則利用式(5)更新相關濾波器模板H，i加1，并返回至步驟2，對第i+1幀圖像進行目標跟蹤。

3 實驗結果及分析

3.1 實驗環境

本文提出的尺度自適應目標跟蹤的實驗環境見表1。

表1 尺度自適應目標跟蹤實驗環境配置 Table 1 Experimental environment configuration of scale adaptive target tracking

3.2 數據集與評價指標

3.2.1 數據集介紹

本文采用的數據集為目標跟蹤標準數據集OTB-100(Online Object Tracking Benchmark)中的6個序列和作者自建的Girl_S 序列。

OTB-100 數據集是最常用的目標跟蹤算法數據集，包含100 個視頻序列。每個序列包含img 文件夾和ground-truth 文件，img 文件夾包含該序列連續的RGB 圖像；ground-truth 文件包含每一幀RGB圖像對應的標定信息，即目標邊框的左上角坐標x，y和目標邊框的寬、高數據。本文選擇跟蹤過程中目標尺度發生變化的 Car2，Human2，Girl2，Crossing，Walking 和Walking2 序列作為實驗數據集。例如，Car2 序列中包含913 幀連續的圖像。序列的目標為一輛在公路上行駛的小轎車，拍攝的相機位于轎車的后方，目標在行駛過程中尺度發生了明顯的變化，并且場景的光照也發生了明暗交替的變化。

自建Girl_S 序列拍攝于西安科技大學臨潼校區圖書館門前，包含200 幀連續圖像序列和每一幀圖像的ground-truth 文件。該序列中的目標是身著橙色上衣的學生，在行走過程中目標的尺度發生了明顯變化，并且在第108～154 幀中，另一名身著黃色上衣的行人出現，對跟蹤目標進行了完全遮擋。

本文使用Car2 序列的前850 幀圖像訓練深度-尺度估計模型；使用其余6 個序列對深度-尺度估計模型進行了測試。

3.2.2 評價指標

本文使用4 種評價指標對算法進行分析。

(1) 成功率。預測框和標定框二者的交集與并集之間的比值大于等于給定閾值的視頻幀數和總幀數的百分比，即

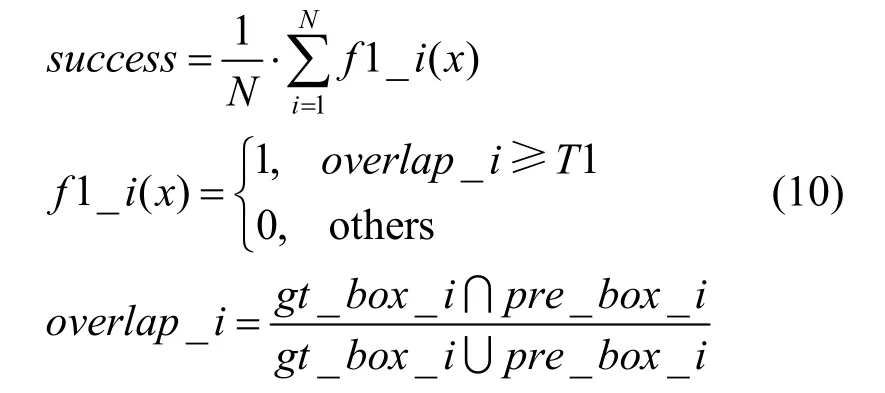
其中，N為視頻的總幀數。gt_box_i和pre_box_i分別為第i幀的標定框和預測框；T1 為閾值，常取值0.5；success為成功率。成功率越大，表示跟蹤的越準確。

(2) 中心位置誤差。預測框中心點坐標與標定框中心點坐標二者之間的歐氏距離，即

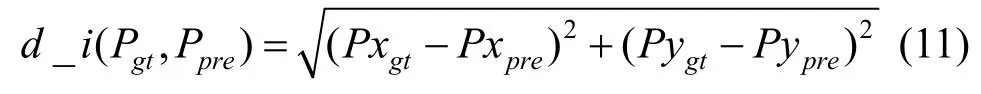
其中，1≤i≤N，N為視頻的總幀數；Pxgt和Pygt分別為標定框中心點的橫、縱坐標；Pxpre和Pypre分別為預測框中心點的橫、縱坐標；d_i(Pgt,Ppre)為2 點之間的歐氏距離。

(3) 精度。中心位置誤差小于給定閾值的視頻幀數和總幀數的百分比，即

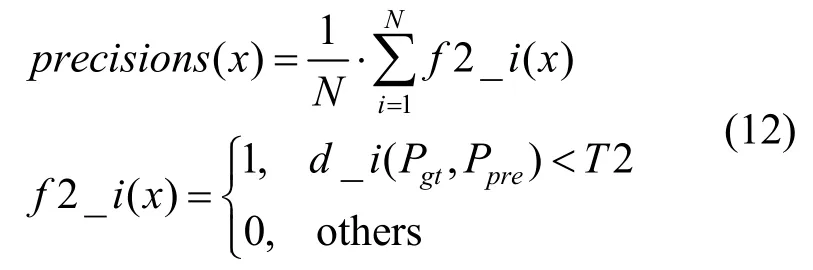
其中，precisions(x)為跟蹤精度，其值越大，表示精度越高；T2 為閾值，常取值20。

(4) 速度。算法所用時間與視頻序列幀數的比值，即平均每秒跟蹤的幀數，值越大則跟蹤的速度越快。

3.3 實驗

3.3.1 深度-尺度估計模型實驗

首先，使用左右一致性單目深度估計網絡，得到Car2 序列中各幀的深度值。

圖4 為Car2 序列中部分幀的RGB 圖像和對應的深度圖像。圖中綠色框標注的是所跟蹤的目標，實驗中使用的尺度值指綠色框的面積，由ground-truth 文件中的長、寬計算得到；深度值指的是深度圖像中綠色框中心位置像素的深度值。

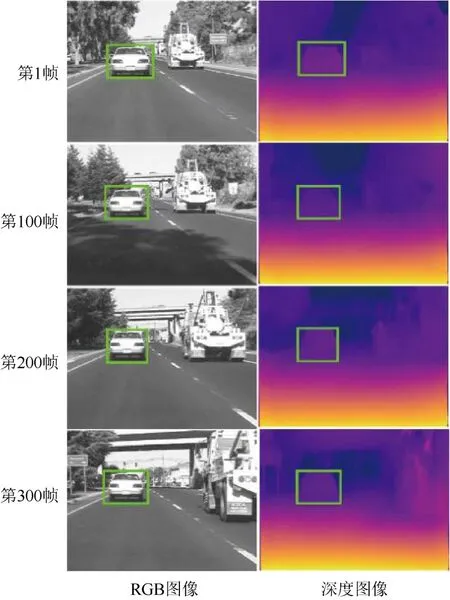
圖4 Car2 部分幀的RGB 圖像和深度圖像 Fig.4 Part of the RGB images and depth images of Car2

圖5(a)中的藍色線為Car2 序列中目標深度值隨幀數的變化情況。可以看出，目標移動過程中，目標和鏡頭的相對位置一直在變化，出現的幾個峰值是因為在跟蹤過程中目標通過橋梁，光照發生了由亮到暗再到亮的變化，可以將其忽略。圖5(b)中的藍色線為Car2 序列中目標尺度值隨幀數變化的情況。可以看出，隨著目標與鏡頭相對距離的改變，目標的尺度逐漸變小，并且趨勢明顯。圖5(a)和(b)中的橙色線分別是對深度值和尺度值平滑擬合后的結果。

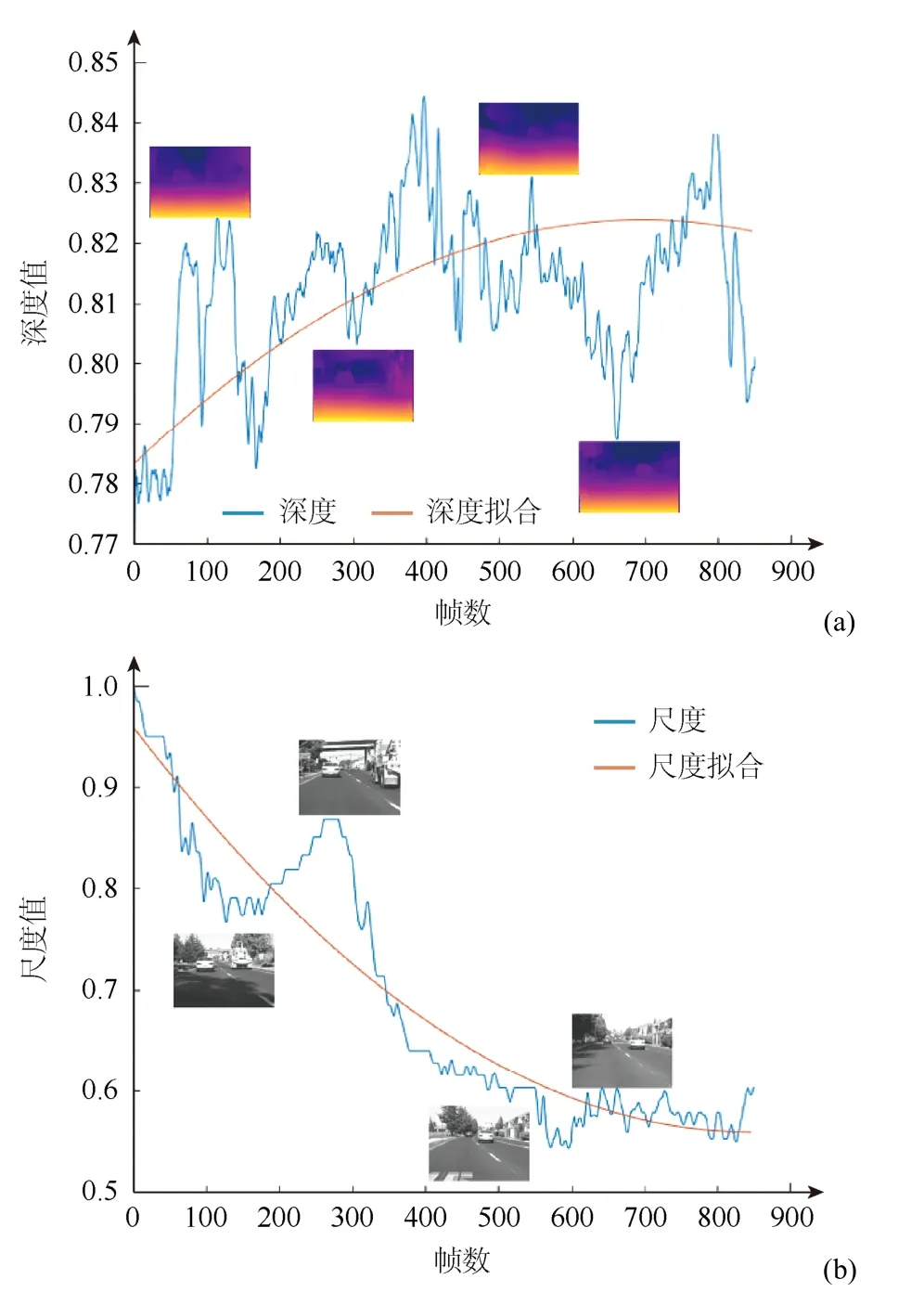
圖5 目標的變化曲線((a)目標深度值曲線圖；(b)目標尺度值曲線圖) Fig.5 Variation curves of target ((a) Plot of target depth values;(b) Plot of target scale values)

圖6(a)中的藍色散點的坐標分別是目標的深度值和尺度值，紅色曲線是直接對其進行擬合的結果。

為了提高模型的可靠性，本文算法首先對離散的深度值和尺度值分別進行平滑處理，經過平滑處理后的深度值與尺度值的散點圖如圖6(b)中綠色星形散點所示，紅色曲線是對平滑處理后的深度值和尺度值進行擬合的結果，即深度-尺度估計模型。

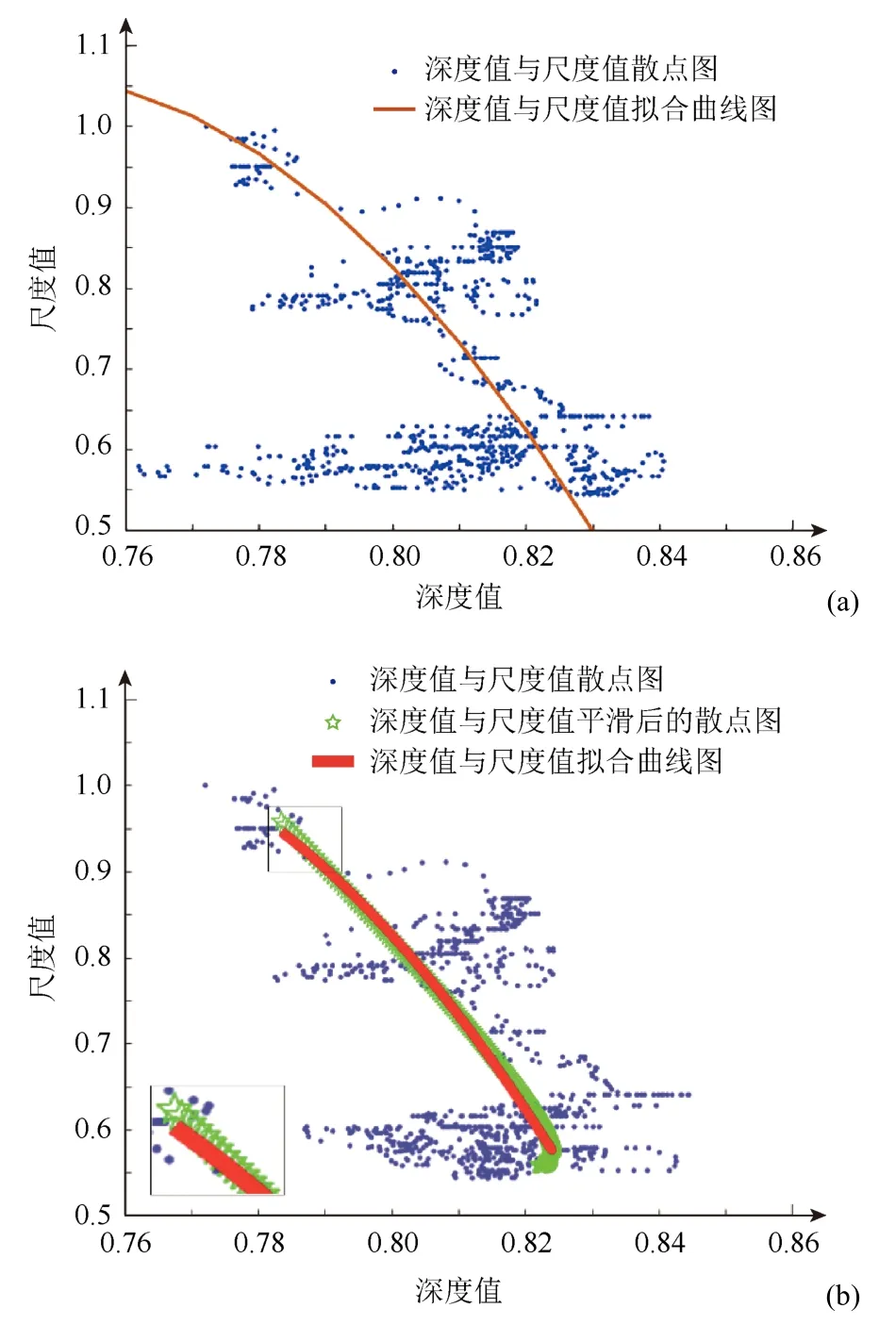
圖6 深度-尺度估計模型((a)未平滑的深度-尺度估計模型；(b)平滑處理后的深度-尺度估計模型) Fig.6 Depth-scale estimation model ((a) Unsmoothed depth-scale estimation model;(b) Smoothed depth-scale estimation model)

3.3.2 尺度自適應跟蹤實驗

為了客觀的驗證本文算法的有效性，在除用于訓練深度-尺度模型的Car2 序列外的6 個目標尺度發生變化的序列上進行測試，并與KCF 算法[10]、DSST 算法[11]進行對比，實驗結果如圖7 和8、表2和3 所示。

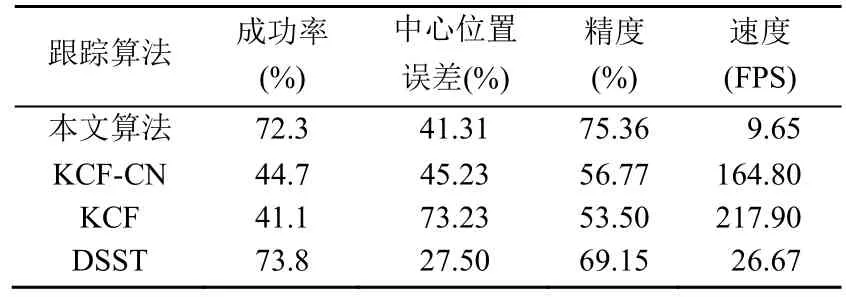
表2 各算法在6個視頻序列的跟蹤結果的平均值 Table 2 Average of the tracking results of each algorithm for 6 video sequences

圖7 對Walking2 序列的跟蹤結果 Fig.7 The tracking result for Walking2

圖7 是在Walking2 序列上的跟蹤結果。可以看出，在第110 幀時，目標尺度發生了明顯變化；在第339 幀時，KCF 的跟蹤框由于尺度過大，導致跟蹤模板污染，跟蹤框失效，在后續幀中丟失了目標，而本文算法和DSST 算法可自適應地調整跟蹤框大小，在后續幀中仍能較準確地跟蹤目標。

圖8 是在Girl_S 序列上的跟蹤結果。可以看到，在第80 幀時，目標尺度發生了變化，DSST 算法的尺度較準確，KCF 未作尺度調整，本文算法的尺度有所變化；在第130 幀時，目標被遮擋，此時，DSST算法估計的目標尺度最準確，KCF 算法的尺度未發生變化，本文算法對尺度做了一定的調整；在第160幀到200 幀，目標通過遮擋后重新出現，DSST 算法發生漂移，跟蹤錯誤；KCF 和本文算法均能夠正確跟蹤目標，KCF 算法的目標尺度固定，而本文算法對尺度做了調整。

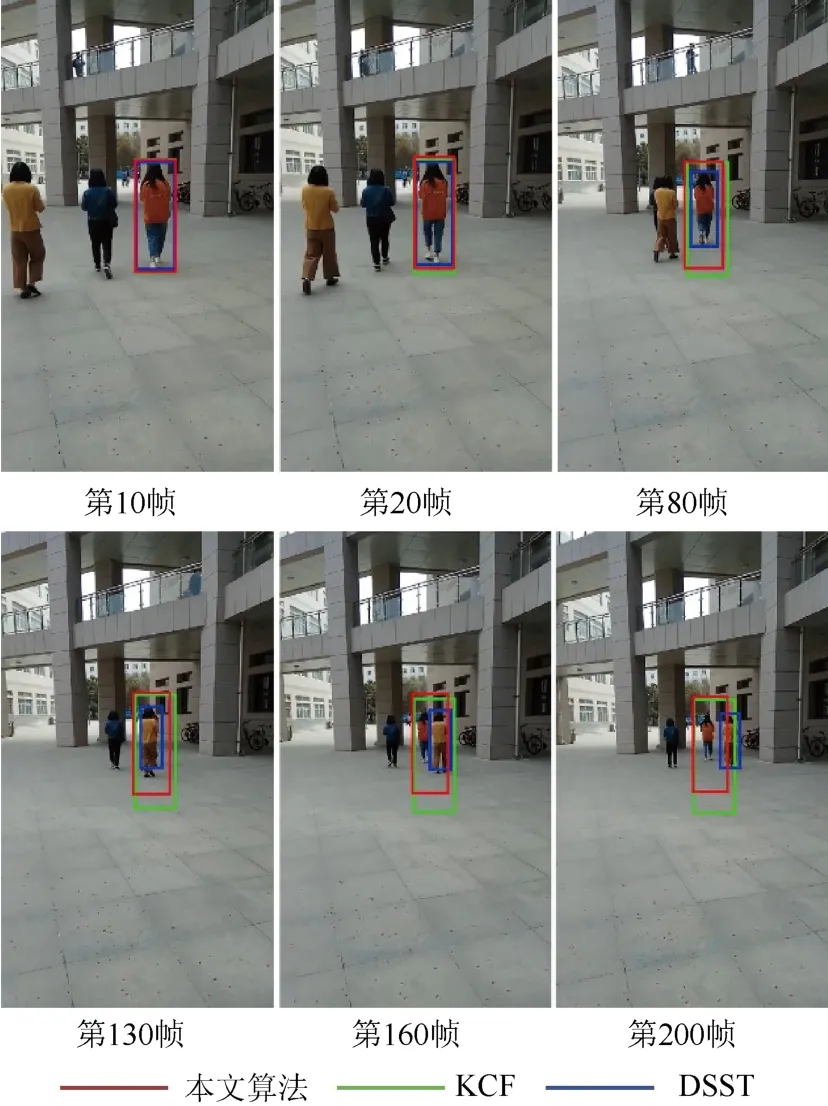
圖8 對Girrl_S 序列的跟蹤結果 Fig.8 The tracking result for Girl_S

將本文算法和采用HOG+CN 特征的KCF-CN算法、僅采用HOG 特征的KCF 算法、DSST 算法分別在6 個視頻序列上測試，得到的成功率、中心位置誤差、精度和速度的平均值見表2。可以看出，本文目標跟蹤算法在跟蹤成功率、中心位置誤差、精度上的表現都優于KCF 算法，但是本文算法的速度明顯低于KCF 算法。這是由于本文算法需要采用左右一致性單目深度估計網絡計算每一幀的深度值。因此，在實時跟蹤時，會明顯降低跟蹤的速度，但依然能夠滿足公園、小區、學校、商場等場景下對低速目標(如行人)實時跟蹤的要求。在非實時跟蹤時，可以首先使用單目深度估計算法，得到所有幀的深度，從而實現更高速的跟蹤。和DSST算法相比，本文算法精度更高。

在表3 中列出了本文算法和對比算法在6 個序列上的成功率、中心位置誤差、精度和速度，其中加粗黑體字為表現最好的算法。本文算法和DSST算法在成功率、中心位置誤差和精度3 個指標中，總體而言表現良好。KCF-CN 算法優于KCF 算法，證明了魯棒的外觀模型可以更充分地表示目標，從而提高目標跟蹤算法的性能。

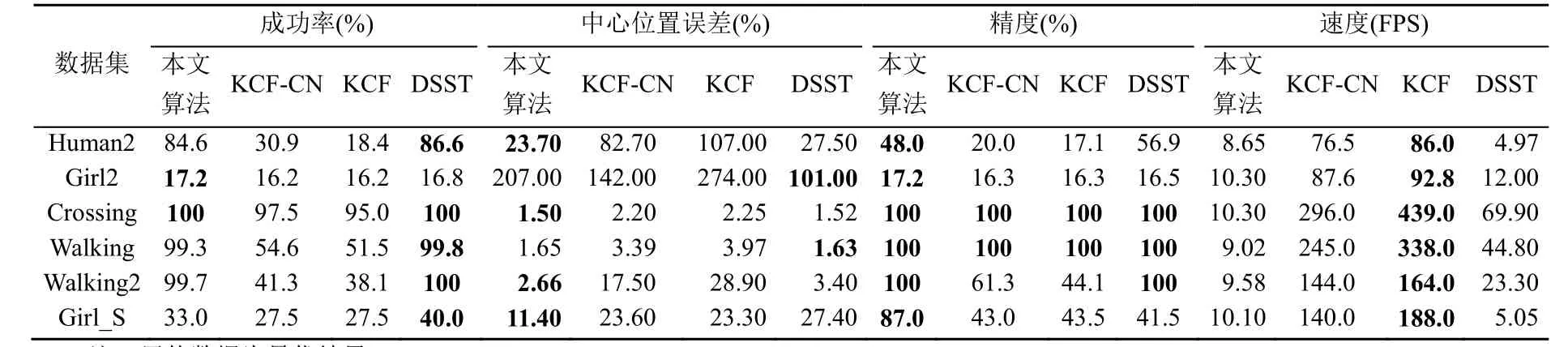
表3 各算法在6個視頻序列的結果對比 Table 3 Comparison of the results of each algorithm in 6 video sequences

在成功率和中心位置誤差指標上，本文算法和DSST 算法在每個視頻序列上的表現都明顯高于KCF 算法。這是因為本文算法和DSST 算法能實時自適應地調整預測框的大小，及時更新濾波模板，所以跟蹤更準確；在精度指標上，Crossing 序列和Walking 序列，與本文算法和DSST 算法都達到了100%，是因為這2 個序列的尺度變化很小，因此，即使KCF 算法不改變濾波模板大小，也能準確地跟蹤目標。而在目標尺度發生較大變化時，本文算法和DSST 算法更準確。

在Human2 序列中，本文算法在成功率和精度指標上略低DSST 算法，是因為該序列光照變化復雜，目標的深度受到影響，估計到的目標尺度不準確，影響了2 個指標，但本文算法始終可以跟蹤到目標，而DSST 算法在跟蹤中，有幾幀未能跟蹤到，所以本文算法在中心誤差指標上優于DSST 算法；在速度上，本文算法快于DSST 算法。

在Girl2 序列中，發生了目標被遮擋的情況。被其他行人完全遮擋的前幾幀，DSST 算法預測就已經發生了偏移，而本文算法是在目標被完全遮擋后才發生了偏移，因此本文算法的成功率和精度略高于DSST 算法；本文算法的中心誤差大的原因是，目標被遮擋后，本文算法預測的位置離目標很遠，DSST 算法雖然未能跟蹤到目標，但是預測的位置并未偏離很大。

自建序列Girl_S 中，在精度和中心位置誤差指標中，本文算法較高，是因為目標被遮擋后，DSST算法跟蹤錯誤，而本文算法并未跟蹤錯誤；在成功率指標中，因為該序列整體亮度較低，在第35 幀后，目標的深度預測不準確，估計的尺度比目標實際的尺度大，所以成功率不高。在速度上，本文算法快于DSST 算法。

綜上，本文算法比KCF 算法在除速度指標外的其他3 個指標上更好；與DSST 算法相比，在尺度變化較大時，跟蹤速度更快；在環境復雜、目標移動過程中出現與目標顏色近似的遮擋物時，魯棒性更好。

圖9 是在不同閾值下，本文算法和對比算法在6 個視頻序列上的平均跟蹤精度。可以看出，本文算法表現最好。

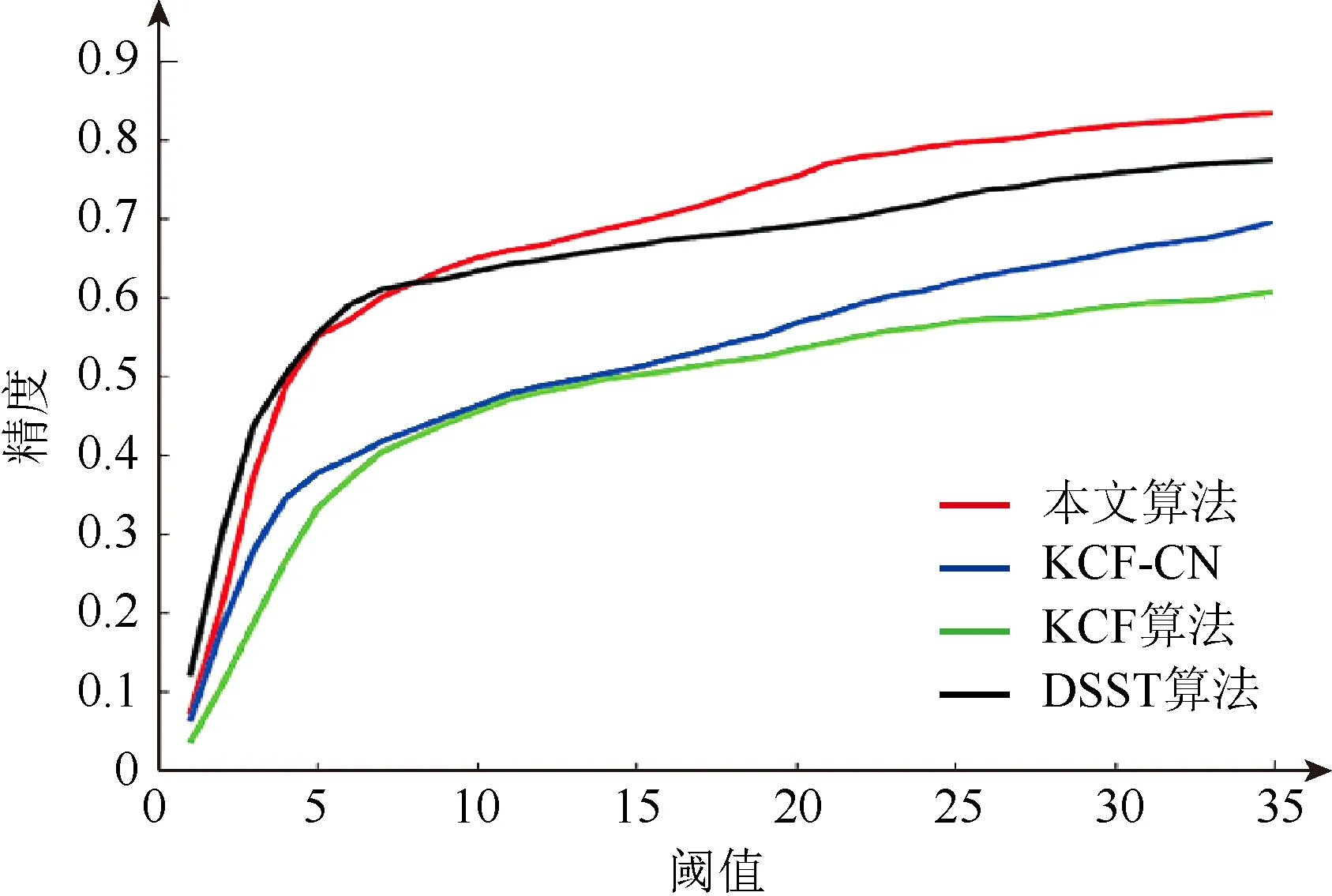
圖9 各算法的跟蹤精度可視化圖 Fig.9 Visualization of tracking accuracy of each algorithm

4 結束語

針對經典核相關濾波目標跟蹤算法在復雜環境下，或目標尺度發生較大變化時，無法準確跟蹤目標的問題，本文提出一種基于深度估計和特征融合的尺度自適應目標跟蹤算法。該算法將HOG 特征和CN 特征相融合建立目標的外觀模型，并通過建立深度-尺度估計模型，實現了尺度自適應的魯棒跟蹤算法。實驗結果表明，和KCF 算法相比，當目標發生明顯尺度變化時，該算法能夠有效提升目標跟蹤的準確率。但是由于引入左右一致性單目深度估計網絡來估計目標的深度值，跟蹤速度較慢，適用于公園、小區、學校、商場等場景下對低速目標的跟蹤，以及非實時跟蹤的場景；和DSST 算法相比，在尺度變化較大時，跟蹤速度更快，在環境復雜、目標移動過程中出現與目標顏色近似的遮擋物時，魯棒性更好。