一種基于比幅比相的星載告警測向方法

韋北余，邢明強，王 建，王利偉，趙 軍，高曉堃，曹 鑫，顧 輝

（1.中國航天科工集團8511研究所，江蘇 南京 210007；2.中國人民解放軍93734部隊，北京 101200）

0 引言

為了應對反衛星武器的威脅，適應復雜電磁環境，迫切需要發展有效的星載寬帶雷達告警測向系統。傳統的雷達告警系統常采用比幅測向技術[1]，廣泛應用于機載平臺。比幅測向技術，利用2個通道接收信號的幅度對比進行測向，這種方法對接收信號的信噪比比較敏感，其測角精度約為3 d B波束寬度的1/10[2]。對于雷達告警天線單元，由于要求瞬時覆蓋的范圍較大，其3 d B波束寬度一般為90°，其對應的比幅測角精度為10°左右，這樣的測角精度能夠滿足飛機告警的需求，但對于星載平臺，由于作用距離遠超機載平臺，相同的測角誤差導致的定位誤差較大，因此，星載雷達告警系統需要采用一種較高測角精度的測角方法。

雷達告警系統主要測向技術為寬帶測向原理，目前常用的方法可分為2種：比幅體制、比相體制[3]。比幅體制的方法主要有基于數字多波束比幅和傳統雙通道比幅方法。其中，數字多波束比幅測向方法采用數字陣列天線，通道數較多，設備量大[4]。比相體制的方法主要為干涉儀測向方法，其測角精度較高，但由于采用多基線提高解模糊能力，天線單元數較多，體積大，設備量較大[5]。星載雷達告警系統作為有效載荷的一部分，由于平臺的特殊性，分配給雷達告警系統的功率、尺寸、質量有限，所以需要采用設備量及功耗較小的測向方法。綜上，適應星載平臺的告警測向方法仍然為傳統的雙通道比幅測向方法，但需要提高其測角精度。針對以上的問題，綜合比幅測向和比相測向的優點，利用比相測向精度高的特點彌補比幅測向精度低的缺陷，本文提出一種基于比幅比相的測角方法。此方法通過比幅測向粗測出信號來波方向，利用比幅測角結果解比相干涉測向的相位模糊，通過長基線干涉測向提高系統測向精度。此外，本文對該方法的測角精度進行了分析，通過仿真驗證了方法的可行性，并仿真分析了此方法的測角精度。

1 比幅比相測向原理

1.1 比幅測向原理

比幅測向利用2天線接收到的信號幅度值之比進行測角，原理圖如圖1所示，采用2個彼此部分重疊的天線波束，在不考慮天線波束副瓣的影響條件下，2天線張角為θa，信號從偏離2波束等信號軸φs角度入射，對于2個天線方向圖，信號從不同的角度入射，2路接收通道信號幅度存在差異，信號入射角度偏離等信號軸越遠，2通道幅度差異越大，因此，通過比較2路信號幅度可以判斷目標偏離角度，實現對目標信號的測向[1?5]。

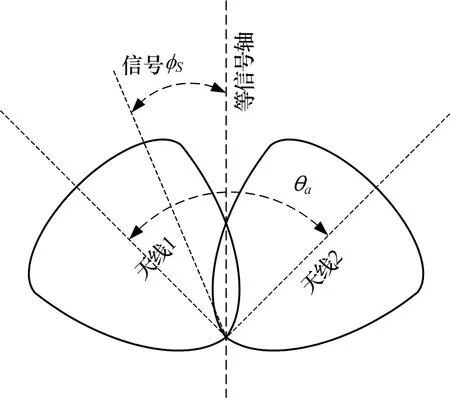
圖1 比幅測向原理圖

在一維測向的條件下，假設天線方向圖函數為F(θ)，通道幅度響應為A c(t)，入射信號幅度A s(t)，入射角度φs，則2通道輸出信號為：

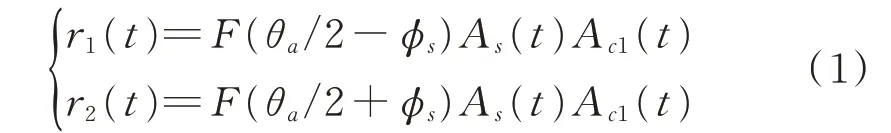
式中，A c1、A c2分別為通道1、通道2的幅度響應。

則2通道接收信號的幅度比為：

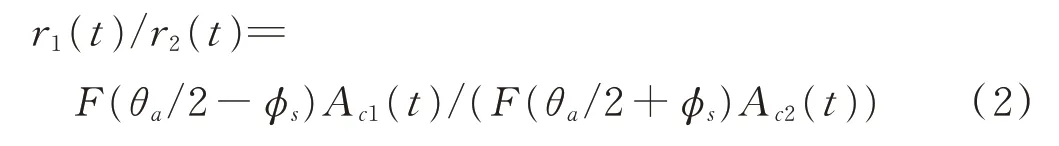
對于同一時刻，用分貝（d B）表示2通道幅度比為：

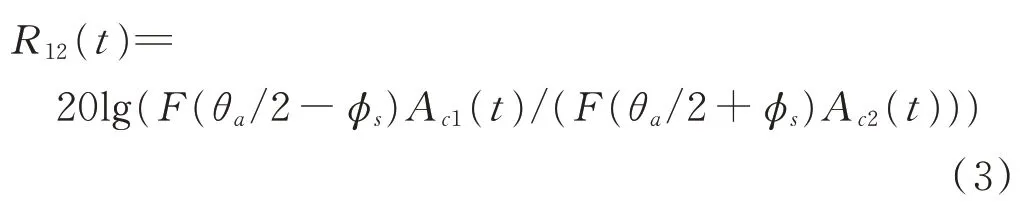
假設2接收通道幅度響應相同，即A c1(t)=A c2(t)，則：

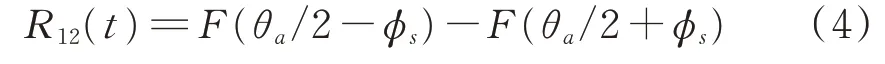
此處F(θa/2?φs)、F(θa/2+φs)為取對數后的分貝值。由于F(θ)在[?θa,θa]范圍內具有單調性，所以2通道比值與信號入射角具有一一對應關系。

假設天線方向圖為高斯函數，即F(θ)=e?kθ2，假設其半功率波束寬度為θb，根據半功率波束寬度定義，即F(θb/2)=2?1/2，可得：

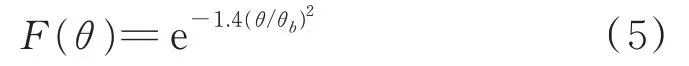
代入式(4)，得到的2通道幅度比值為：

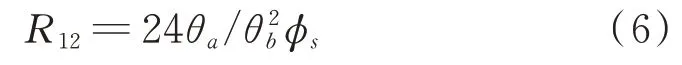
可以看到，2通道幅度比值與信號入射角一一對應，只要知道2通道幅度比，便可獲知信號來波方向。

1.2 比相測向原理

比相測向利用多個天線所接收回波信號之間的相位差進行測角[7-8]，比相測向原理圖如圖2所示。

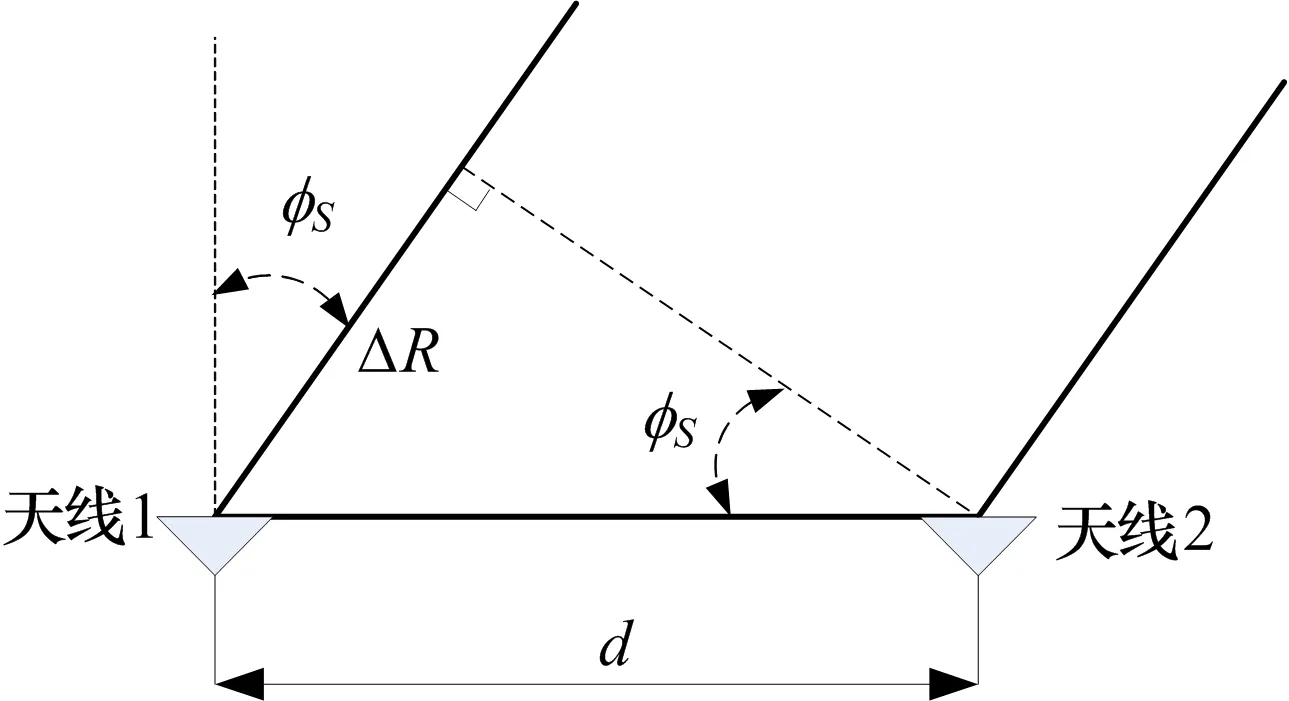
圖2 比相測向原理圖

在遠場平面波的假設條件下，由于天線間存在間距d，信號到達2個天線時間不同，由波程差ΔR產生的相位差為φ，由圖2可知：

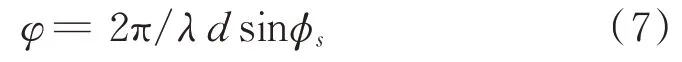
式中，λ為輻射源的波長。如果能夠測得φ，則可確定信號來波方向φs。

1.3 比幅比相測向

比幅比相測向方法綜合比幅及比相測向方法，先利用比幅測向粗測出信號入射角度，再利用比相測向精測量信號入射角。此方法需要根據比幅測角的精度進行設置，因此，要設定比幅比相天線陣列布置，必須先研究比幅測向及比相測向的測角精度。

對于比幅測向，根據式（6），可得：

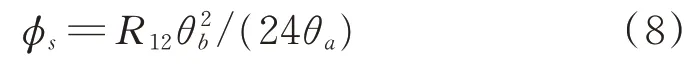
對式（8）中θa、θb、R12求全微分，得到：

式中，Δφs為角度測角誤差；Δθa為2波束張角；Δθb為天線波束3 dB寬度；ΔR12為通道幅度比誤差。可以看出：波束半功率波束寬度θb越小，即波束越窄，測角誤差越小；2波束張角θa越大，測角誤差越小；2通道比幅值越小，即信號入射方向越靠近等信號軸，測角誤差越小；θa、θb、R12的變化對測角誤差都有影響。以上比幅精度的推導未考慮天線波束副瓣的存在，天線主波束變窄的同時，天線波束副瓣必然升高，若信號從副瓣進入，信號入射方向與通道幅度比值成非單調關系，將影響比幅測向結果，導致不可測向，因此，天線主波束寬度不可無限小，同理，2波束張角也能過大。所以，波束寬度和波束張角的變化，不能破壞通道幅度比值與信號入射方向的單調性，否則將導致測向模糊。

對于固定天線陣，同一頻率信號，其波束寬度及波束指向皆固定，則測角誤差可表示為：

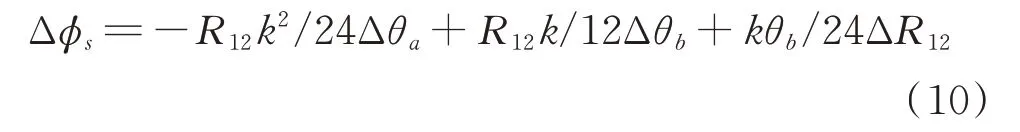
式中，k=θb/θa，為常數。θa、θb、R123個誤差因素中，Δθa、Δθb屬于靜態誤差，工程實現中可以通過校表等方法校正；ΔR12為動態誤差，即通道幅度響應隨工作環境變化，無法提前校正。從式（10）最后1項可以看出：在等信號軸處R12=0 d B，波束寬度及張角對比幅測角誤差影響最小，在波束指向方向R12最大，波束寬度及張角對測角誤差影響最大；通道幅度比誤差對測向誤差的影響程度，主要由波束寬度決定，波束越窄，測角誤差對通道幅度比值的誤差敏感度越小，測向精度越高。

對于比相測向，對式（7）進行微分，可得測向誤差的表達式，為：

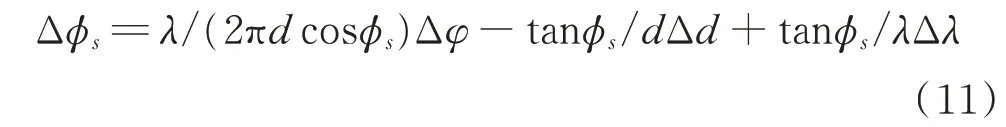
式中，Δφs為角度測量誤差；Δφ為2通道相位差鑒相誤差；Δd為基線長度測量誤差；Δλ為由測頻誤差導致的波長測量誤差。Δφ、Δd、Δλ3個測量誤差中，Δd為靜態誤差，工程實現中可在設備工作前測量校正；Δφ、Δλ為動態誤差，無法提前校正。

對于波長測量誤差導致的測向誤差Δφλ，可表示為：

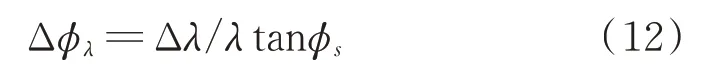
假設測頻誤差為Δf，則：

式中，f0為信號真實載頻；c為光速。所以，Δφλ可進一步表示為：

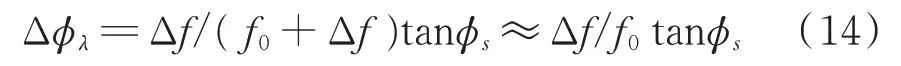
由于Δf相對于中心頻率f0較小，能夠達到1%以下，且測量的φs范圍通常限制在±π4以內，所以對應的測角誤差Δφλ較小，可以忽略，所以角度測量誤差則主要由通道間相位差鑒相誤差決定，即：

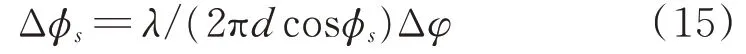
式中，λ、φs由輻射源信號特征決定，d為比相基線長度，由天線布置設定。可以看出，d越大，測角精度越高。但是，d越大，測得的φ越大，當|φ|＞π時，通道間相位差測量值將存在相位模糊，必須先解模糊才能測向。

比相測向相位模糊示意圖如圖3所示，圖中φa為測向模糊周期，只有在φa寬度的角度范圍內，測量的通道間相位差φ與信號入射角φs一一對應，不存在模糊情況。由式（7）可知，d＞λ2時，通道相位差存在相位模糊，λ2對應不模糊入射角范圍，d對應180°所有入射角可能性，則φa為：

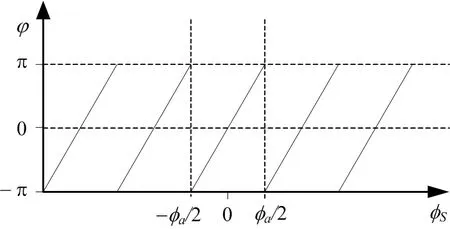
圖3 比相測向相位模糊示意圖

如果要利用比幅測角方法解比相測角相位模糊，則比幅測向結果必須保證不超過比相測角的模糊范圍，才能保證后續比相測角結果的唯一性。假設信號真實入射角為φs0，比幅測角精度為Δφae，比幅比相測向原理如圖4所示。

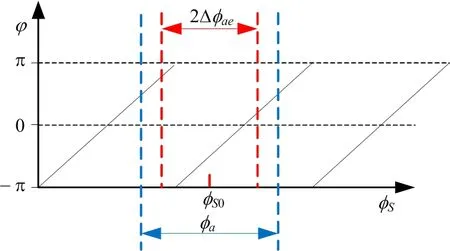
圖4 比幅比相測向原理圖

從圖4中可以看出，利用比幅測角方法解比相測角相位模糊，必須滿足2Δφae≤φa條件。根據式（10），忽略靜態誤差因素，則：

比幅比相測向可解模糊的基線長度條件為：

假設系統設計要求的測角精度為Δφs0，根據式（15），可得天線基線長度d為：

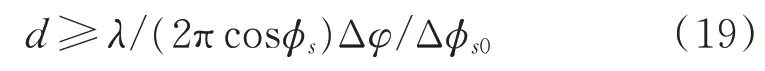
綜合式（18）和式（19），可得比幅比相測向方法天線基線長度d限制范圍為：

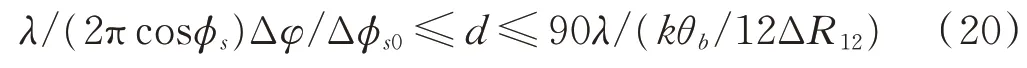
對于寬帶雷達偵測系統，其工作頻段較寬，對應的波長變化較大，最長、最短波長比可達3倍以上，假設接收信號波長變化范圍為[λmin,λmax]，由于式（20）的條件為針對單個頻點的限制，對于整個系統，為保證測向精度，其最短工作基線應該選擇最大值，同理，為保證比相測向可解模糊，最長工作基線應選擇最小值，所以比幅比相測向方法天線基線長度d限制范圍可修改為：

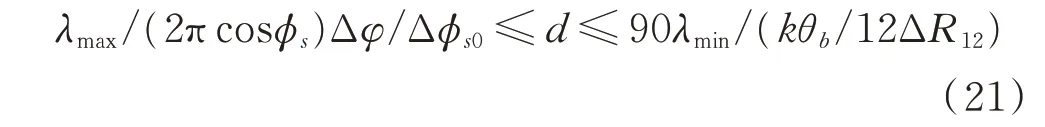
綜上，比幅比相測向系統基線設計步驟如下：

1）根據工作頻段要求的測角精度及接收信號的最長波長計算最短基線長度要求；

2）根據接收信號的最短波長、比幅測角精度計算最長基線限制；

3）比較最長最短基線要求，如果兩者相矛盾，即最長基線小于最短基線，則此工作波段寬度條件下，無法采用單基線比幅比相測角，需修改工作頻段寬度，或采用雙基線、多基線方案。

1.4 二維比幅比相測向

前文的測向為一維測向，星載雷達告警系統需要測定輻射源的空間二維角度信息，需要進行二維測向。

星載雷達告警測向示意圖如圖5所示，輻射源位于衛星的可視區域，需要測定的輻射源角度信息為(α1,β1)，其中，α1為方位角，β1為俯仰角。實際實現中常采用柱體坐標系來定義輻射源的方位角與俯仰角，其與衛星載體坐標系的關系如圖6所示，此時的輻射源方位及俯仰角為(α,β)。

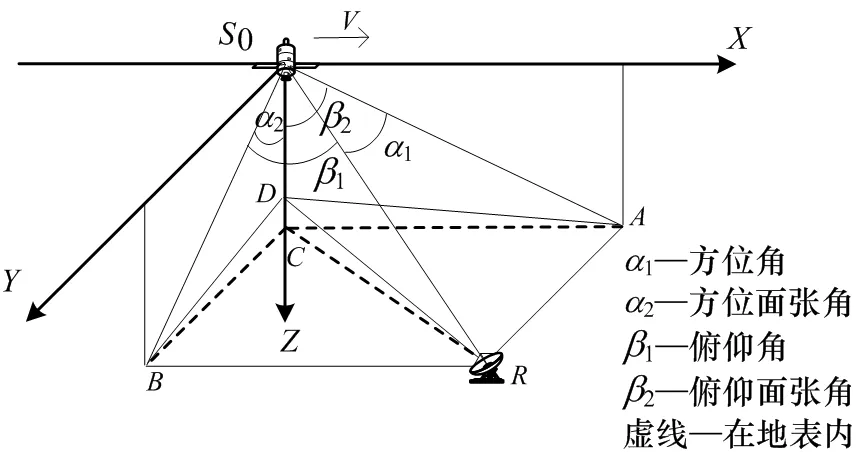
圖5 星載雷達告警測向示意圖

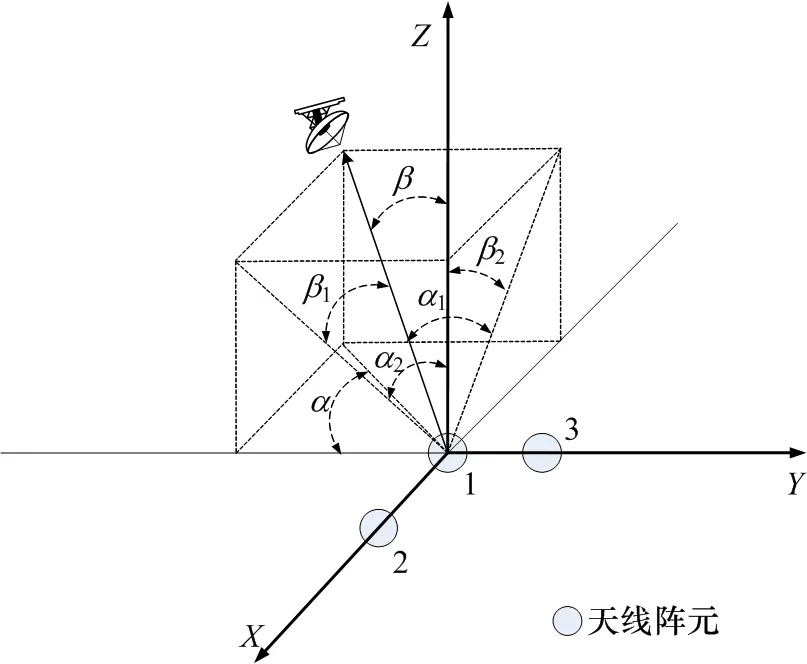
圖6 柱體坐下系比幅比相二維測向示意圖

為減少設備量及通道數，本系統采用三陣元天線陣。三陣元天線方向圖相同，但波束指向不同，以Z軸為中心軸，在空間中均勻分布，如圖7所示。天線1、天線2、天線3波束方位角α分別為225°、0°、90°，3個波束指向與Z軸夾角相同，即波束指向的俯仰角β相同，此時天線2、天線3相對于天線1的幾何關系是等價的，即若天線方向圖在三維空間內關于波束中心線完全對稱，則此天線陣在X軸、Y軸方向的測角能力相等。

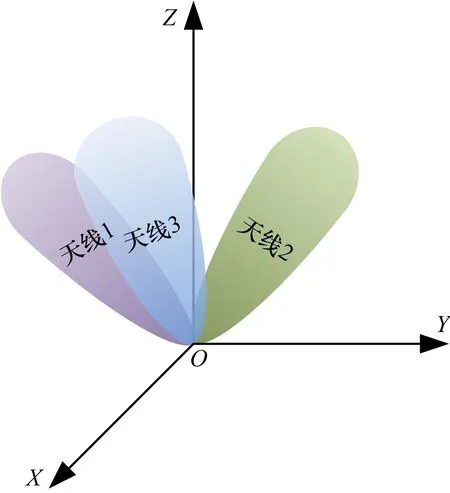
圖7 波束指向示意圖

在圖7的天線波束指向的條件下，波束沿XOZ面的剖面如圖8所示。與一維測向的情況不同，此時天線3與天線1、天線2的波束并不對稱，天線波束在空間上存在交疊。

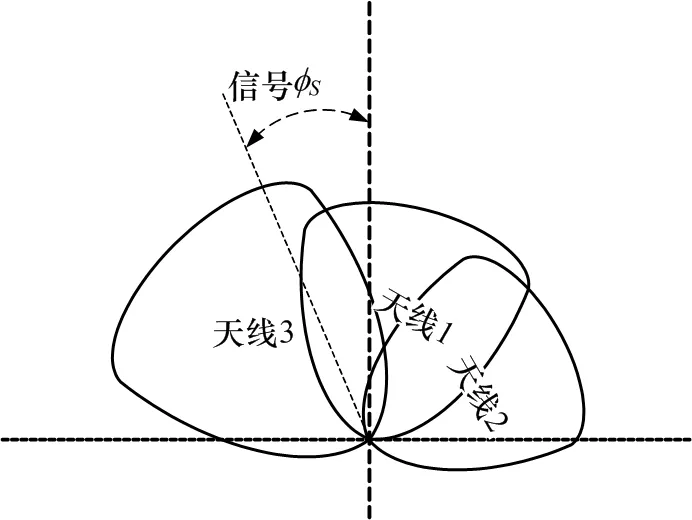
圖8 三波束剖面示意圖

由于天線增益、波束指向已知，所以波束幅度增益差固定，因此，仍然可以采用比幅方法進行測向。3個天線波束，可以組成3組比幅測角天線對，即每2個天線可以得到一組天線幅度增益差ΔF，將某一方向的3 個 幅 度 差 組 成 向 量X(α,β)，X(α,β)=[ΔF12;ΔF13;ΔF23]，其中，ΔF12為天線1與天線2的天線幅度增益差，同理，可得到ΔF13、ΔF23。3個幅度差變量中，ΔF12、ΔF13是相互獨立的不相關變量，由于天線交疊區域內天線間的幅度差具有單調性，所以輻射源角度與3通道幅度差向量一一對應，假設測定的3個通道間相位差為Y，可以通過Y與X的相關系數來判斷輻射源的角度，相關系數最大的向量X對應的角度就是輻射源的入射角度。假設信號入射角度的空間樣本個數為N，則二維比幅測角可表示為：

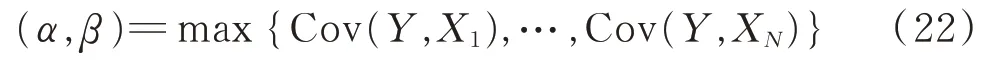
在某一角度上，由于二維比幅測角相對于一維測角多了1個獨立變量，其測角魯棒性更強，即測角誤差對通道間幅度誤差敏感度較一維比幅測角低。

通過比幅測向得到目標入射角度的粗測結果，可以確定方位角度搜索范圍，進一步通過比相測角，得到高精度的測角結果。

對于本系統的三陣元的二維比相測角，其測角過程與一維比相測角不同。在一維比相測角中，2個天線波束的指向相同，在入射信號為平面波的假設下，信號從2個天線波束的同一角度入射，所以每個天線波束的相位對于信號的影響相同，在測量通道間相位差的時候，能夠消除天線相位對信號相位的影響，僅剩余由天線基線導致的通道間相位差。而本系統的比相二維測向中，3個天線波束指向不同，接收信號時，同一信號從天線波束的不同角度入射，造成同一信號在每個通道疊加了不同的相位信息，通道間取相位差時，無法去除天線方向圖相位特性對信號相位的影響，所以同一信號通道間相位差包含了由天線基線產生的相位和2個通道對應天線方向圖相位的差，因此，無法簡單地通過式(7)計算輻射源的入射角度。

對于一定方向入射的信號，其對應的天線波束相位差固定，且由波程差導致的相位同樣固定，因此，參照比幅測向方法，可以建立信號入射相位表，即對空間入射角度的所有可能性建立通道相位差查找表，但是由于比相測向的特殊性，與比幅測向不同，其相位差在整個測角空域范圍內并非單調，存在相位模糊現象，這主要由天線基線過長所造成的，因此，比相測向前需要通過比幅測向粗測出信號波方向，然后在比相測向的一個模糊方位內進行搜索，確定輻射源角度信息。

不同于一維測向的相位模糊周期，3陣元模糊周期較長，這是由于3組通道間相位差的組合造成的，二維比幅比相相位模糊示意圖如圖9所示。

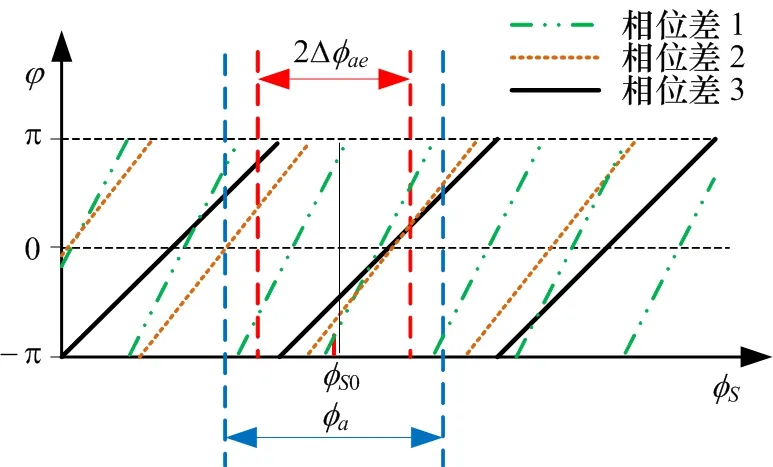
圖9 二維比幅比相相位模糊示意圖

3陣元天線系統中，存在3組陣元組合，即存在3條測向基線，同一信號從不同空間角度入射，3條基線的模糊周期不同，組合后如圖9所示。3組相位差有各自的模糊周期，二維比相測角同時利用3組相位差進行測角，即使某一組或2組存在相位模糊，只要其中一組在整個搜索區間內單調，與角度一一對應，即可確定來波方向，完成測角。所以，二維比相測角的模糊周期為3組相位差模糊周期的最大值。

如前文所述，二維比相中，除基線導致的通道間相位差，還存在從天線波束不同方向入射導致的相位差，因此，實際的周期結果與圖9有差異，不同角度位置對應的通道間相位差會包含不同的波束相位差，導致各通道相位差周期性產生變化，甚至失去周期性。但是，由于采用3通道相位差測向，只要3組相位差在搜索區間內存在一組與角度一對一的相位差，即可完成二維比相測向。

綜上，對于二維比幅比相，式（21）中基線長度d除遵循一維比幅比相測角的限制外，還需要根據實際天線增益、指向及布陣情況進行合理的調整。

2 仿真分析

2.1 仿真模型

仿真系統采用3陣元“L”型布局，天線陣布局幾何模型如圖6所示。3個陣元完全相同，天線的工作波段為2~6 GHz，波束寬度90°，在柱體坐標系下，3個天線的波束指向的方位分別為225°、0°、90°，俯仰角為40°，其空間位置如圖6和圖7所示。假設通道間相位誤差15°，通道間幅度誤差1 dB，根據式（21）計算，得到0.08 m≤d≤0.57 m，根據實際情況設定的天線1與天線2、天線3的間距為0.14 m。

選取2 GHz、4 GHz、6 GHz 3個頻點進行仿真實驗，并將天線波束的方位角及俯仰角變換到衛星載體坐標系下，即從(α,β)坐標變換為(α1,β1)，3個頻點對應的天線方向圖幅度圖如圖10所示，天線方向圖的相位如圖11所示。

對比圖10中的3幅圖，可以發現，高頻點的波束寬度較低頻點窄，即θb較小，高頻點的波束主瓣增益比低頻點的高，偵測系統天線的瞬時覆蓋范圍由高頻點的波束寬度θb決定，天線波束寬度及增益的變化，會影響比幅測向的精度。

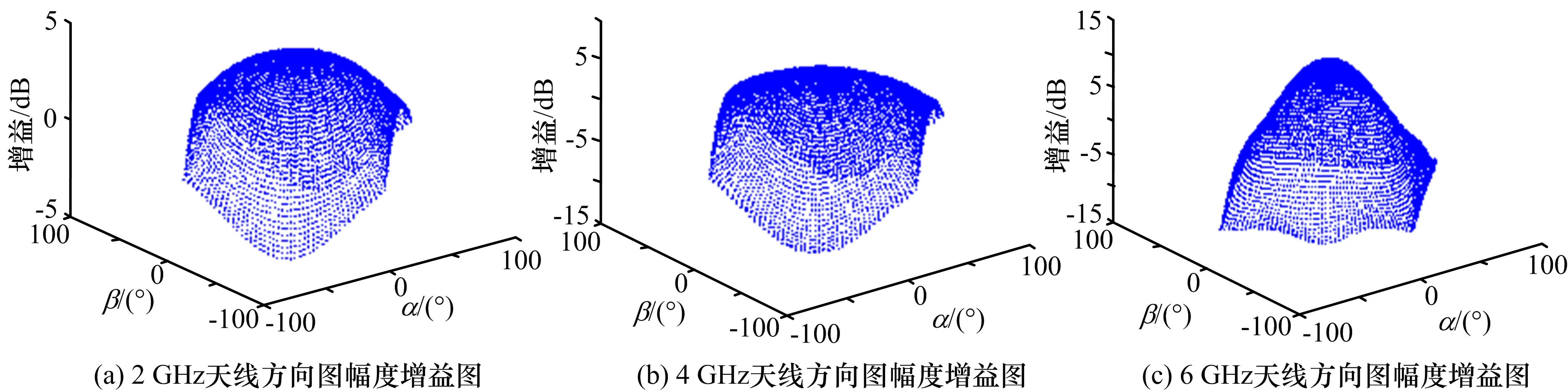
圖10 天線方向圖幅度增益圖

從圖11中可以看出，3個頻點的天線方向圖相位自身存在相位模糊現象，6 GHz的天線波束相位模糊情況最為嚴重。由于3個波束指向不同，這種相位模糊導致同一空間角度不同通道間的相位差復雜化，這種模糊不利于后續的比相測角。

圖11 天線方向圖相位圖

以4 GHz頻點波束方向圖為例進行進一步仿真分析。按照設定的波束指向，將同一波束進行旋轉變換，得到3個指向不同的波束，3天線波束幅度增益空間疊加圖如圖12所示，相位疊加圖如圖13所示。

從圖12可以看出，3個波束在空間交叉疊加，在同一空間角度，3個波束對應的幅度增益不同，利用這種增益差異，能夠實現二維測向。

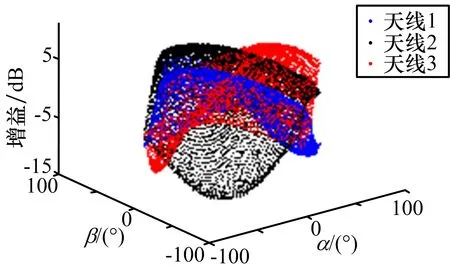
圖12 天線方向圖幅度疊加圖

如圖13所示，由于3個天線波束相位本身存在相位模糊現象，3個波束相位圖交疊后較為復雜，但同時可以發現，同一空間角度對應的3個波束的相位不同，利用這種相位差異能夠實現比相測向。

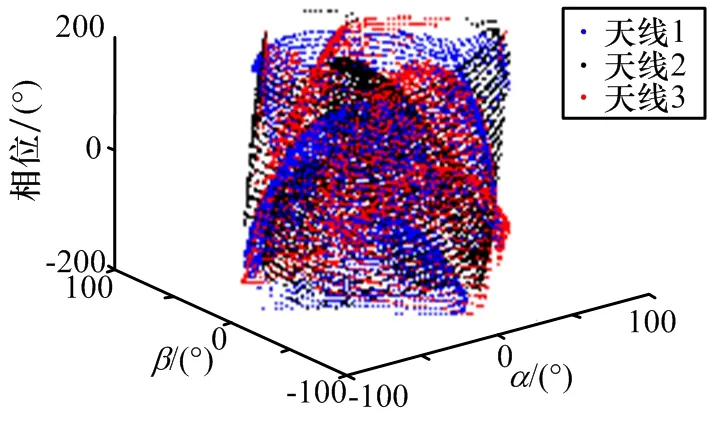
圖13 天線方向圖相位疊加圖

根據同一空間角度對應的幅度增益值，分別求天線1、天線2、天線3波束之間的幅度增益差，得到的結果如圖14所示。

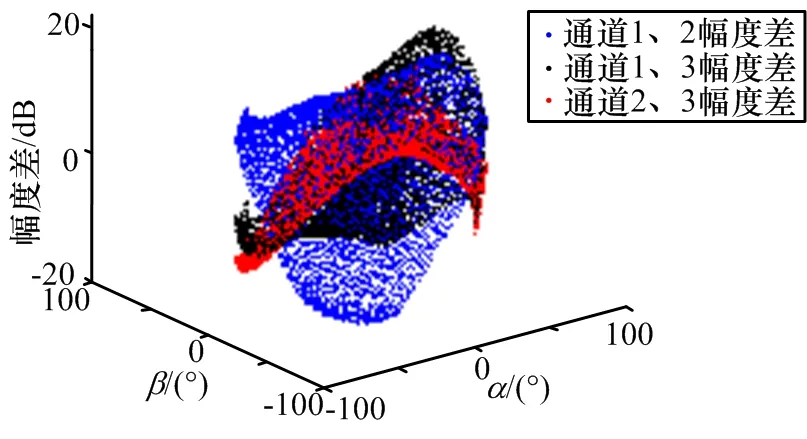
圖14 天線方向圖幅度差

從圖14可以看出，3組幅度增益差在空間內較為平滑，無較大波動，即幅度增益差在空間內具有單調性，3組幅度增益差的組合與空間角度一一對應，能夠用于二維測向。

為更清楚地觀測幅度差測向的原理，分別沿俯仰角0°面、方位角0°面對幅度差進行剖面分析，得到的結果如圖15所示。

圖15中，3個通道間幅度差在整個測角范圍[?45°,45°]內具有單調性，與信號角度一一對應，同時可以看到，3個通道間幅度差數值不同，任一角度對應的3個幅度差值具有唯一性，這有利于后續的相關比幅測向處理。

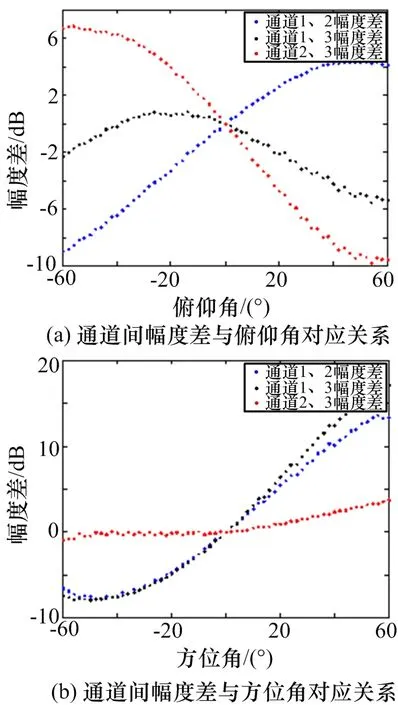
圖15 天線方向圖幅度差圖兩維剖面圖

與比幅測向類似，根據同一空間角度對應的各天線波束相位，及各天線幾何位置導致的相位差，分別求天線1、天線2、天線3對應通道間的相位差，得到的結果如圖16所示。

如圖16所示，各天線間的相位差較為復雜，但仍呈現模糊特性，需要通過解模糊方法校正。

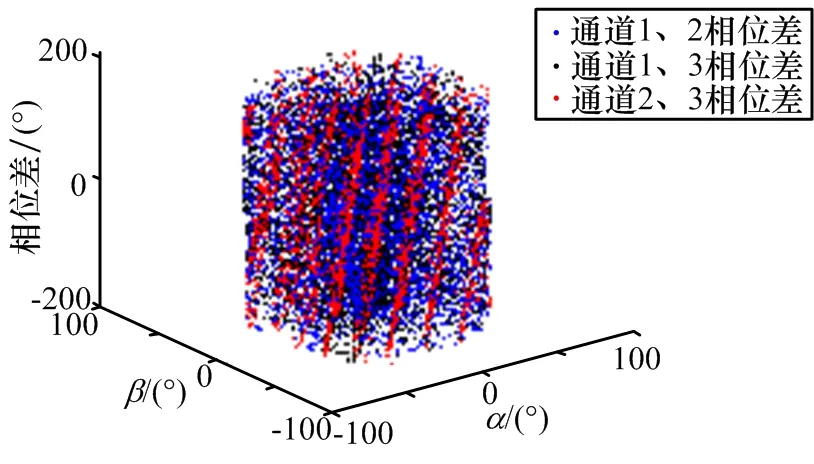
圖16 天線方向圖幅度差圖兩維剖面

同樣，為更清晰地觀測通道間的相位差變化規律，分別沿俯仰角0°面、方位角0°面對通道間相位差圖進行剖面分析，得到的結果如圖17所示。

從圖17可以看出，3組通道間相位差存在一定的周期性，但重復周期不固定，且有變化，這是由于通道間相位不僅包含信號到天線的距離差導致的相位，還包括2個天線波束間的相位差。由于相位差規律性較差，導致最終的相位差無固定周期，只是呈現一定的周期性，但是，從圖17中可以看出，在一個重復周期內，至少有2組相位差具有單調性，同一角度對應的3組相位差具有唯一性，因此，此相位差能夠用于測向。

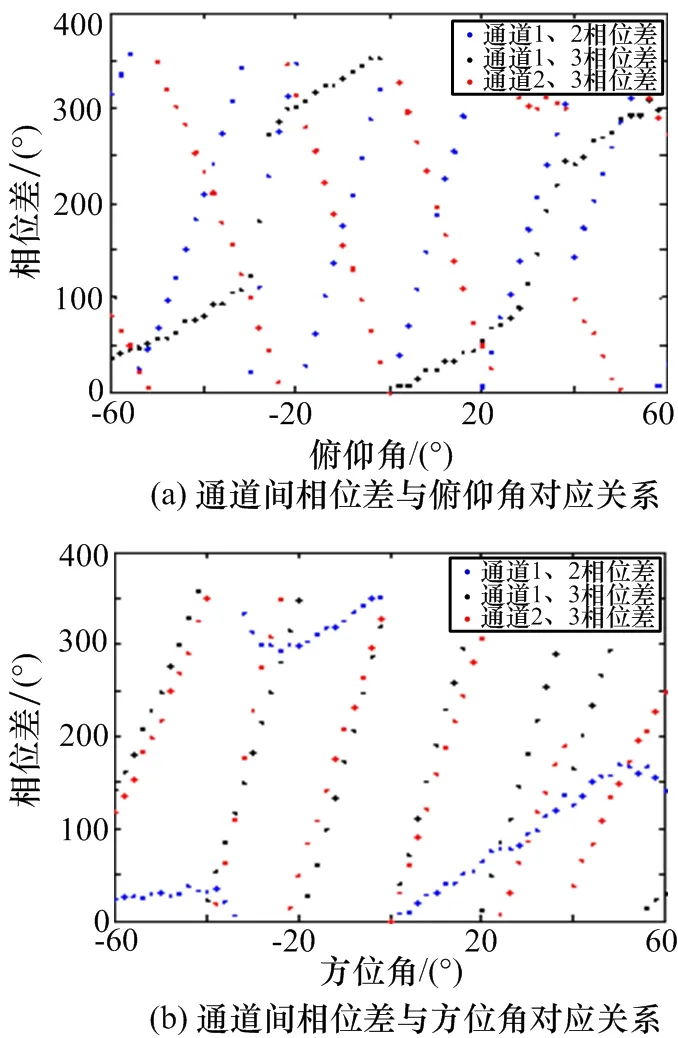
圖17 通道間相位差圖兩維剖面圖

2.2 測角誤差仿真

根據前文仿真模型，在柱體坐標系下，以10°為間隔在方位維0°~360°范圍內設置仿真點，以5°為間隔在俯仰維0°~45°范圍內設置仿真點，每個點進行100次蒙特卡羅仿真，仿真不同頻率對應的測向誤差。以4 GHz頻點為例，假設系統通道間相位誤差15°，通道間幅度誤差1 d B，設置的比相模糊范圍為10°，將所有仿真點的所有測角結果按照測角誤差從小到大進行排序，得到的二維比幅比相測向誤差如圖18所示。

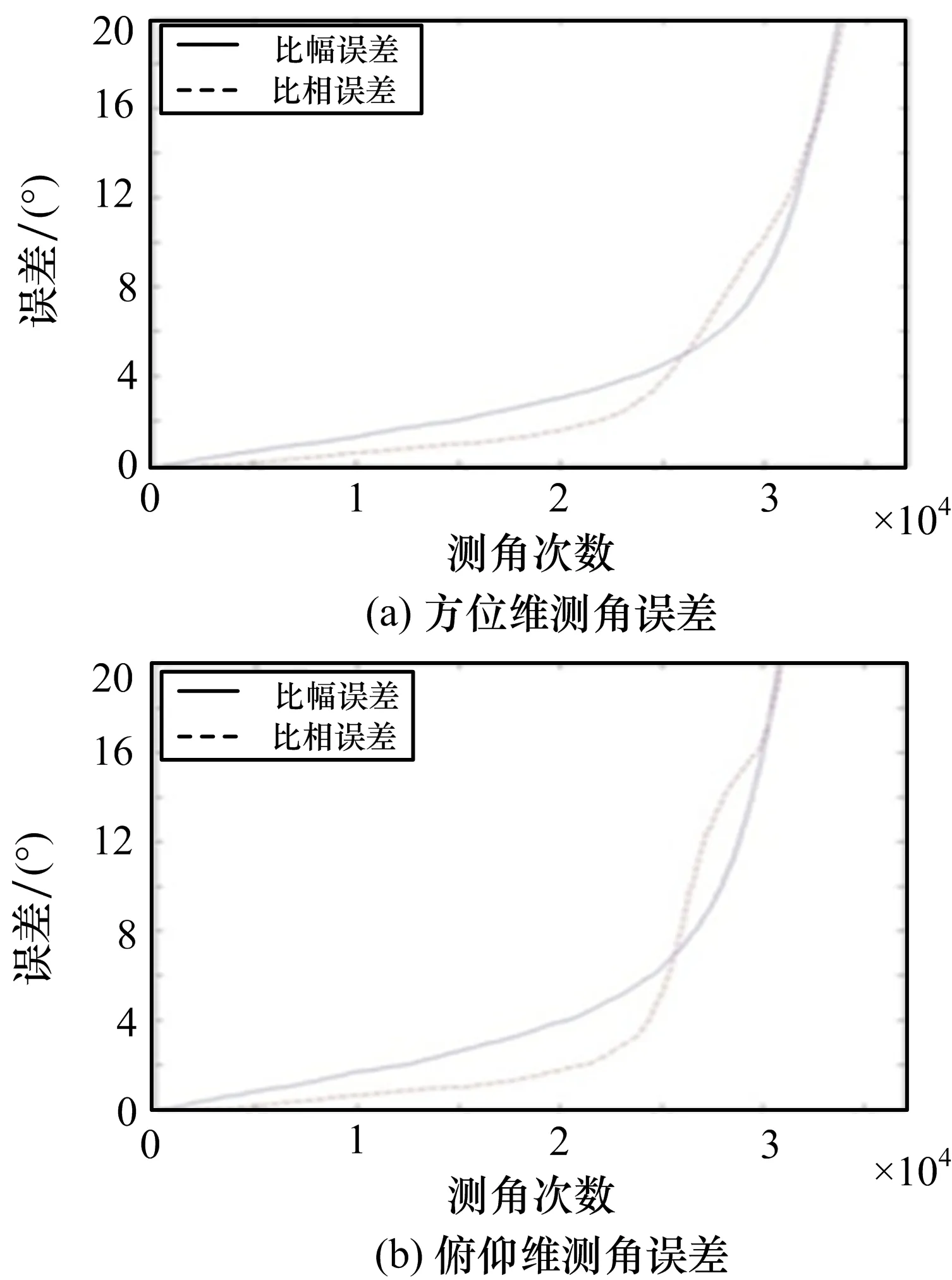
圖18 二維比幅比相測向誤差圖

在圖18中，比幅誤差曲線為僅采用比幅測角的誤差結果，比相誤差曲線為采用比幅比相方法測角的誤差，可以看到，前半段比幅比相誤差明顯比比幅誤差小，后半段比幅誤差與比相誤差曲線交疊，這是由于當比幅比相測角是在比幅測角的基礎上進行比相測角，需要根據比幅測角結果搜索比相測角結果，搜索范圍為一個模糊區間，當比幅測角誤差較大時，偏離信號真實方向較大，此時搜索區域不包含真實角度，導致比相測角得到的角度為其模糊角度，測角誤差有可能變得更大。圖18中比幅誤差曲線與比幅比相誤差曲線的第一個交叉點基本上為測角誤差的方差值，符合正態分布的3σ準則，為第一個σ點。同時可以看出，方位維和俯仰維測角誤差曲線稍有不同，這是由天線方向圖并非360°完全對稱造成的。

為比較各頻點測角性能的差異，本文還仿真2 GHz和6 GHz頻點的比幅比相測角誤差，并同4 GHz頻點進行了比較，結果如圖19所示。

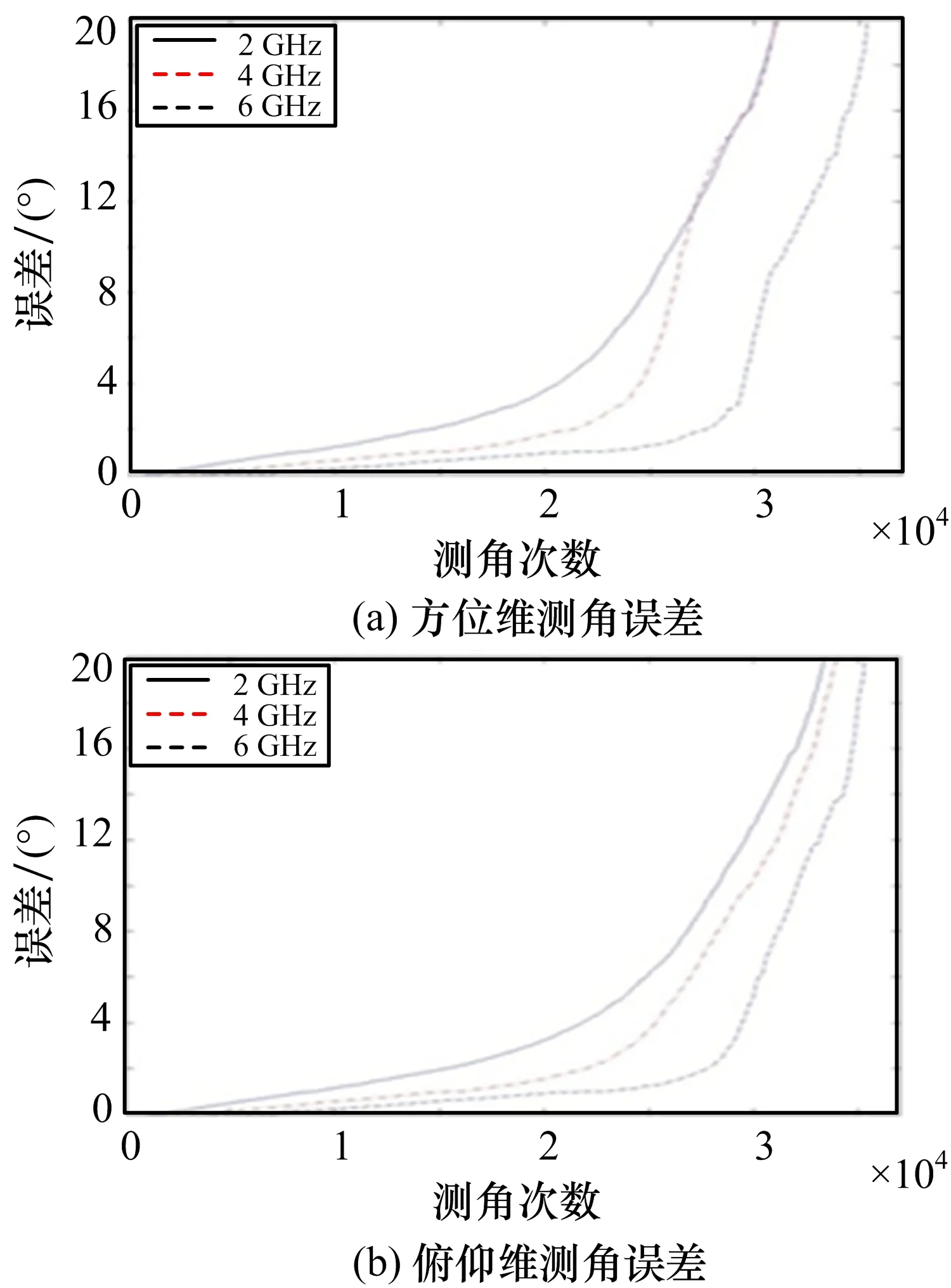
圖19 3頻點比幅比相測角誤差對比圖

從圖19可以看出，3個頻點的測向精度，6 GHz最高，2 GHz最低，這是由于天線在高頻點的3 d B波束較窄，有利于比幅測向，所以，其比幅比相測向精度更高。

為研究通道間幅度測量誤差對比幅比相測角誤差的影響，本節還仿真了不同幅度測量誤差條件下的比幅比相測角誤差，通道間幅度測量誤差為0.3~1.5 d B，仿真結果如圖20所示。

從圖20可以看出，比幅比相測角誤差隨幅度誤差增大而增大，且增速隨幅度誤差增大而增大。

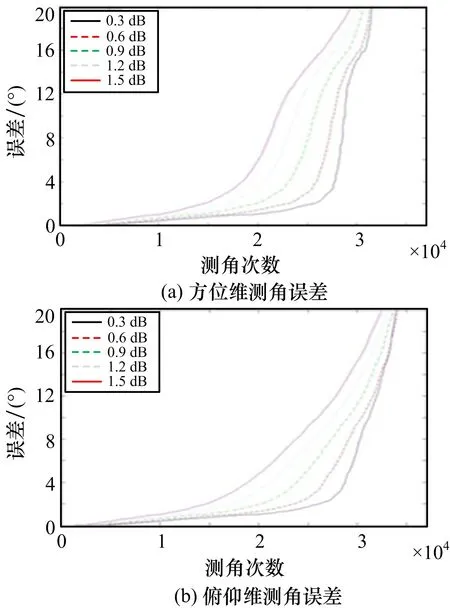
圖20 比幅比相測角誤差隨通道間幅度誤差變化曲線

類似的，在通道間幅度測量誤差為0.9 d B的條件下，本節仿真分析了通道間相位誤差對比幅比相測向誤差的影響，通道間相位誤差從0°變化到16°，得到的仿真結果如圖21所示。

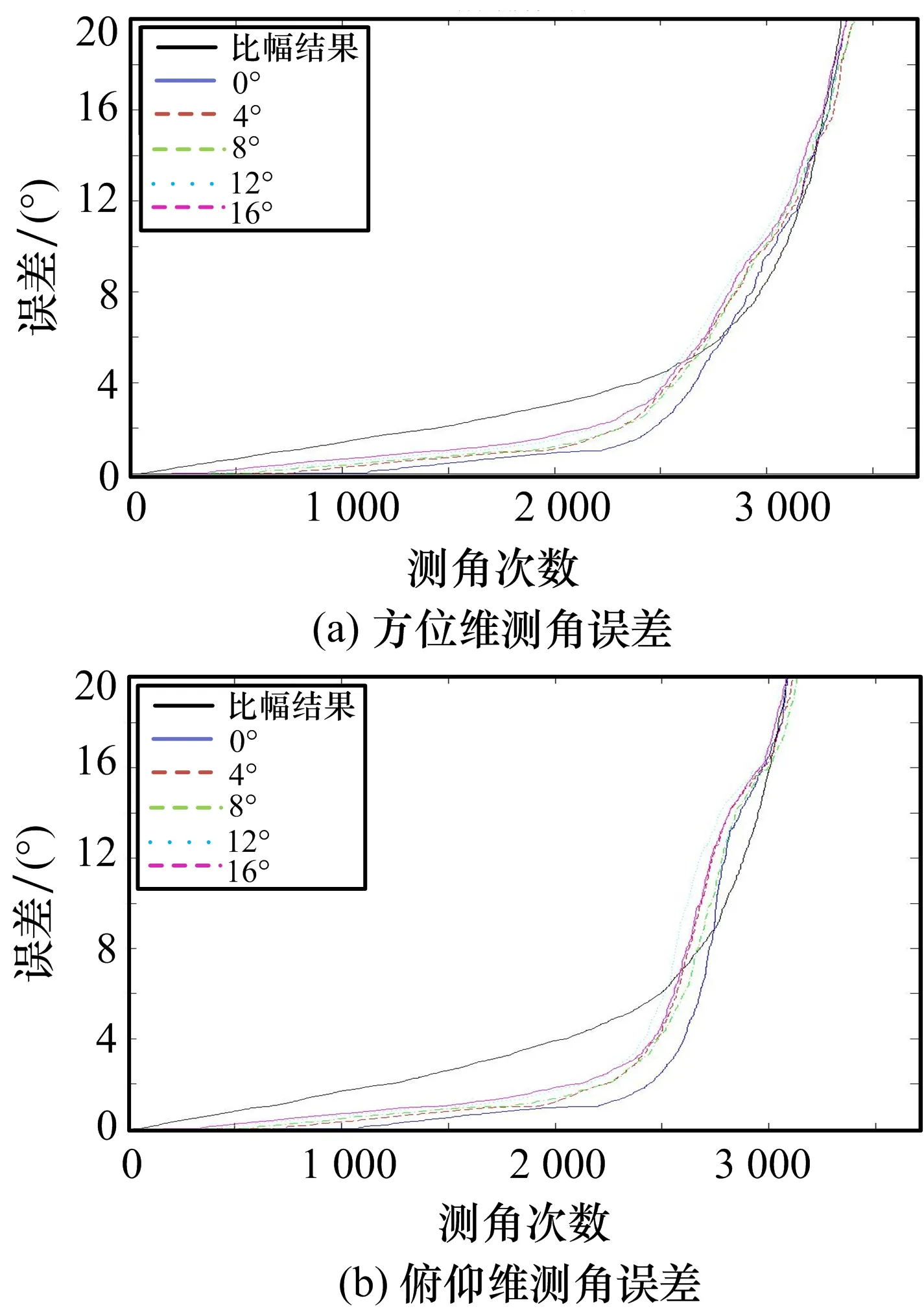
圖21 比幅比相測角誤差隨通道間相位誤差變化曲線

如圖21所示，比幅比相測角誤差隨通道間相位誤差增大而增大，但與單獨的比幅測角結果相比，均有明顯的降低，與圖20對比，比幅比相測向誤差結果隨相位變化較為緩慢，說明此方法收相位誤差的影響較小，測角誤差較為穩定。

3 結束語

本文針對傳統雷達告警系統測向精度較低的問題，提出了一種基于比幅比相的星載告警測向方法，分析了二維比幅比相測向原理，建立了仿真模型，仿真分析了二維比幅比相測向性能，并對通道間幅度及相位誤差對測向誤差的影響進行了仿真分析。仿真結果表明，所提的二維比幅比相方法具有可行性，能夠顯著提高傳統比幅測向的測向精度，增強告警雷達的告警能力。相關技術可應用于多種平臺，用于監測和告警威脅，具備廣闊的應用前景。■