排序問(wèn)題之時(shí)標(biāo)流線圖繪制仿真實(shí)現(xiàn)


摘要:在排序問(wèn)題(Sequencing Program)中,當(dāng)工序道數(shù)M≥3時(shí),計(jì)算總加工時(shí)間常用的方法便是繪制時(shí)標(biāo)流線圖,但在教學(xué)過(guò)程中手工繪圖相對(duì)煩瑣,因此,筆者開發(fā)的網(wǎng)絡(luò)規(guī)劃仿真模塊不僅實(shí)現(xiàn)了時(shí)標(biāo)流線圖的自動(dòng)繪制,而且形象直觀,經(jīng)教學(xué)實(shí)踐,效果良好。
關(guān)鍵詞:排序問(wèn)題;工期;時(shí)標(biāo)流線圖;模擬仿真
Abstract: During the sorting problem (sequencing program),And when the number of steps m≥3,The common way to calculate the total processing time is to draw the time scale streamline diagram. But in the process of teaching, manual drawing is relatively cumbersome. Therefore, The network planning simulation module developed by the author not only realizes the automatic drawing of time scale streamline diagram. And the image is intuitive, through teaching practice, the effect is good.
Key words: sequencing problem; time limit for a project; Timeline Flow Chart; analog simulation
流程調(diào)優(yōu)又稱排序問(wèn)題(sequencing program),亦稱工件加工安排問(wèn)題,是一類典型的組合優(yōu)化問(wèn)題,它一直是運(yùn)籌學(xué)研究的熱點(diǎn)和難點(diǎn)之一。N個(gè)產(chǎn)品在M道工序的加工排序問(wèn)題之M×N模型,當(dāng)各產(chǎn)品加工次序相同時(shí)稱流水作業(yè),當(dāng)各產(chǎn)品之加工次序不同時(shí)也稱加工作業(yè),顯然流水作業(yè)是加工作業(yè)的特殊情況。雖然當(dāng)M=2時(shí),通過(guò)約翰遜定理可得最優(yōu)解,但當(dāng)M≥3時(shí)該問(wèn)題卻是典型的NP問(wèn)題[1],目前尚無(wú)最優(yōu)解求解算法。
1 流程調(diào)優(yōu)
雖然約翰遜定理號(hào)稱解決了M=2時(shí)的排序問(wèn)題,但他給出的只是產(chǎn)品的最優(yōu)加工順序,并未對(duì)最后的總加工時(shí)間作出公式性結(jié)論,實(shí)用中需通過(guò)手動(dòng)繪制時(shí)標(biāo)流線圖來(lái)計(jì)算總工期。筆者曾給出了基于給定加工順序時(shí)的表上工期遞推算法[2],但計(jì)算相對(duì)復(fù)雜煩瑣,并不利于課堂教學(xué)。考慮教學(xué)過(guò)程中對(duì)排序問(wèn)題求解算法原理的形象和直觀性要求,筆者在開發(fā)《軍事運(yùn)籌學(xué)原理仿真模擬系統(tǒng)》(已獲軟著登記)時(shí)針對(duì)流程調(diào)優(yōu)中的時(shí)標(biāo)流線圖也做了專門設(shè)計(jì),后經(jīng)教學(xué)實(shí)踐,效果良好。圖1即“流程調(diào)優(yōu)”模塊的操作主界面。
其中的“M×N模型”按鈕和“1×N模型”按鈕分別維護(hù)的兩種模型的具體加工數(shù)據(jù),因在1×N模型中,關(guān)注的角度一般不再是總加工時(shí)間,而是諸如平均等待時(shí)間之類的轉(zhuǎn)換思路[3],所以,單獨(dú)設(shè)置了操作界面。當(dāng)M=2時(shí),可以利用圖1中的“約氏解法”模擬約翰遜定律之求解示意,鑒于本文的重點(diǎn)是時(shí)標(biāo)流線圖,故這里對(duì)“約氏解法”不再做詳細(xì)說(shuō)明。基于同樣的原因,本文也不再對(duì)“分組法”“分界法”和“窮舉法”逐一介紹。
2 M×N模型之時(shí)標(biāo)流線圖
在圖1所示之操作主界面中,單擊“M×N模型”按鈕即可打開該子模塊[4],如圖2。
M×N排序模型比較復(fù)雜。其模型規(guī)模,即M和N的值,可通過(guò)圖1中的“設(shè)置”命令按鈕來(lái)設(shè)定(細(xì)節(jié)從略),圖2即6道工序(M=6)、8個(gè)產(chǎn)品(N=8)時(shí)的模型狀態(tài)示意。當(dāng)然,圖中的數(shù)據(jù)是通過(guò)隨機(jī)模式自動(dòng)產(chǎn)生的,亦可手動(dòng)維護(hù)之[5]。其實(shí),使用中亦可通過(guò)“導(dǎo)入”命令按鈕將以前保存的模型數(shù)據(jù)導(dǎo)入當(dāng)前系統(tǒng),亦可將當(dāng)前的模型數(shù)據(jù)“保存”起來(lái)以備后用。模型數(shù)據(jù)維護(hù)完備后,單擊圖1中的“流線圖”命令按鈕,即可自動(dòng)繪制當(dāng)前M×N排序模型以當(dāng)前默認(rèn)的產(chǎn)品加工順序時(shí)的時(shí)標(biāo)流線圖,圖3所示就是一個(gè)6道工序7個(gè)產(chǎn)品的時(shí)標(biāo)流線圖繪制結(jié)果。
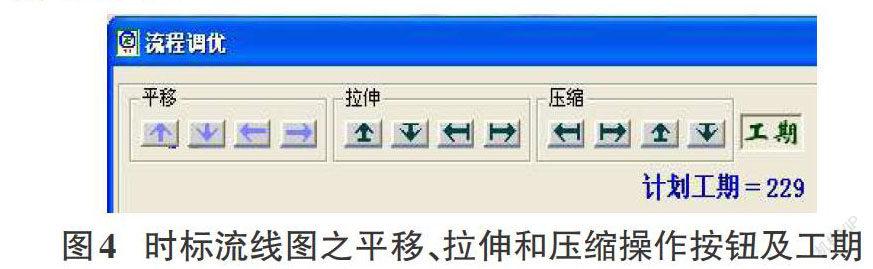
時(shí)標(biāo)流線圖繪制完成后,可通過(guò)屏幕左上角的三組藍(lán)色箭頭,對(duì)流線圖做適當(dāng)處理,諸如平移、拉伸和壓縮等操作。當(dāng)鼠標(biāo)移動(dòng)到“工期”文本框時(shí),當(dāng)前模型對(duì)應(yīng)之總加工時(shí)間即顯示出來(lái),如圖4。
3 時(shí)標(biāo)流線圖設(shè)計(jì)與實(shí)現(xiàn)
為盡量滿足仿真的實(shí)用性,考慮仿真軟件的最大產(chǎn)品數(shù)為50,最大工序數(shù)為20,加工時(shí)間取值范圍為1-50。為方便后面對(duì)各時(shí)標(biāo)流線的靈活控制或處理,還設(shè)置了移動(dòng)、拉伸、壓縮等諸多操作。將每個(gè)產(chǎn)品對(duì)應(yīng)之每道工序的加工時(shí)間都用一個(gè)線性控件來(lái)表示。繪制時(shí)標(biāo)流線圖之前,須根據(jù)當(dāng)前排序模型的實(shí)際狀態(tài),提前計(jì)算并設(shè)置(或顯示)流線圖坐標(biāo)之水平標(biāo)尺線(像素點(diǎn)),而縱坐標(biāo)始終在框架高度之中間(像素點(diǎn)),橫向從左邊界開始至框架右邊界。每隔一個(gè)時(shí)間單位(可在“設(shè)置”模塊中靈活改變)做標(biāo)記。其對(duì)應(yīng)部分VB代碼如下:
接著還需計(jì)算當(dāng)前排序模型對(duì)應(yīng)之各示意流線的坐標(biāo)(像素點(diǎn))。先計(jì)算第一項(xiàng)產(chǎn)品之第一道工序?qū)?yīng)的流線坐標(biāo),再計(jì)算第一道工序上所有產(chǎn)品對(duì)應(yīng)的流線坐標(biāo)(第一個(gè)產(chǎn)品除外,它已經(jīng)賦值),還得計(jì)算第一個(gè)產(chǎn)品在各道工序上加工時(shí),對(duì)應(yīng)的流線坐標(biāo)(第一道工序除外,它已經(jīng)計(jì)算完成),最后計(jì)算當(dāng)前排序模型中,第2道工序及其以后的,從第2個(gè)產(chǎn)品開始的所有加工時(shí)間對(duì)應(yīng)之流線,以及各分隔線,即第一道工序中各產(chǎn)品之分隔線、各道工序最后一產(chǎn)品之分隔線等內(nèi)容。
當(dāng)然,以時(shí)標(biāo)流線圖繪制為基礎(chǔ),結(jié)合分組和分界等算法,考慮教學(xué)過(guò)程中小規(guī)模模型窮舉仿真之可能性,當(dāng)可輕松解決M≥3時(shí)該排序問(wèn)題的最優(yōu)解分析,但限于篇幅,暫且從略。
因水平所限,不妥和錯(cuò)誤之處,敬請(qǐng)大家批評(píng)指正!
參考文獻(xiàn):
[1] 錢頌迪.運(yùn)籌學(xué)[M].北京:清華大學(xué)出版,1993.
[2] 曹迎槐.基于工期求解的排序模型算法設(shè)計(jì)與實(shí)現(xiàn)[J].電腦知識(shí)與技術(shù),2014,10(18):4280-4283.
[3] 曹迎槐,尹健,梁春美.軍事運(yùn)籌學(xué)[M].北京:國(guó)防工業(yè)出版社,2013.
[4] 曹迎槐,張靜,趙強(qiáng).矩陣對(duì)策之降階算法設(shè)計(jì)與實(shí)現(xiàn)[J].信息系統(tǒng)工程,2020(10):121-122.
[5] 曹迎槐.LP模型標(biāo)準(zhǔn)化教輔軟件設(shè)計(jì)與實(shí)現(xiàn)[J].電腦知識(shí)與技術(shù),2018,14(17):87-88.
【通聯(lián)編輯:謝媛媛】

