豐富教材內容 凸顯方程本質

于偉玲

[摘 要]方程是小學數學中重要的概念。在尊重教材的基礎上，文章深入挖掘教材，將方程的形式化表征與其蘊含的思想內涵有機融合，突出等量關系在列方程中的重要作用，讓學生經歷建立方程模型的過程，凸顯方程本質，建構方程概念。

[關鍵詞]方程本質;等量關系;建模

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）23-0067-02

“方程的意義”是人教版教材五年級上冊第五單元的教學內容，是學生學習代數知識的開始，它實現了從算術思維向代數思維的重大跨越。學生在學習中需要經歷把實際問題抽象為方程模型，也就是建模的過程，如何滲透這數學建模思想，體現方程的核心價值，這是教師面臨的挑戰。

一、關于“方程的意義”教材的編排

教材編排“方程的意義”時是以連環畫（5幅圖片）的形式呈現的，第一幅圖：由天平左右兩端平衡引出等式;第二幅圖：天平平衡，發現空杯子的質量是100克;第三幅圖：空杯子中加水后顯然比100克重;第四幅圖：兩次調試，由方程不平衡引出不等式;第五幅圖：第三次調試方程平衡，由一杯水重250克列出含有未知數的等式。最后脫離天平模型列出含有未知數的等式，總結方程的意義。

教材內容很簡單，教師是應該遵循教材，還是拋棄教材，進行大刀闊斧地創新呢？筆者查閱了各個版本的教材，對比和分析后發現，大多數都是采用天平這個媒介引入等式和方程，再也沒有比天平作為等式的模型更直觀，更利于學生理解了。“天平”這一形式化的媒介，生動揭示了方程概念的內涵和外延。這是一節課題研究課，借助視頻動態演示能體現信息技術在小學數學教學中的應用優勢。基本的教學思路已經清晰：尊重教材的基礎上深入挖掘教材內容，豐富方程的內涵。

怎樣才能講出方程的本質和內涵呢？著名數學家陳重穆教授指出：“‘含有未知數的等式叫方程這樣的定義要淡化，不要記，無須背，更不要考。關鍵是要理解方程思想的本質以及它的價值和意義。”因此，要改變常規課堂中緊扣方程字面意義的局面，從靜態定義轉向讓學生積極主動地動態建構對方程的認識，從表面深入其本質，真正領悟方程的思想精髓。

二、此“等式”，非彼“等式”

教材中第一幅圖的天平左邊有2個50克砝碼，右邊有一個100克砝碼，天平處于平衡狀態，要求學生列出一個等式，為接下來利用天平認識方程提供了有利的支撐。

【教學片段1】

演示天平平衡：

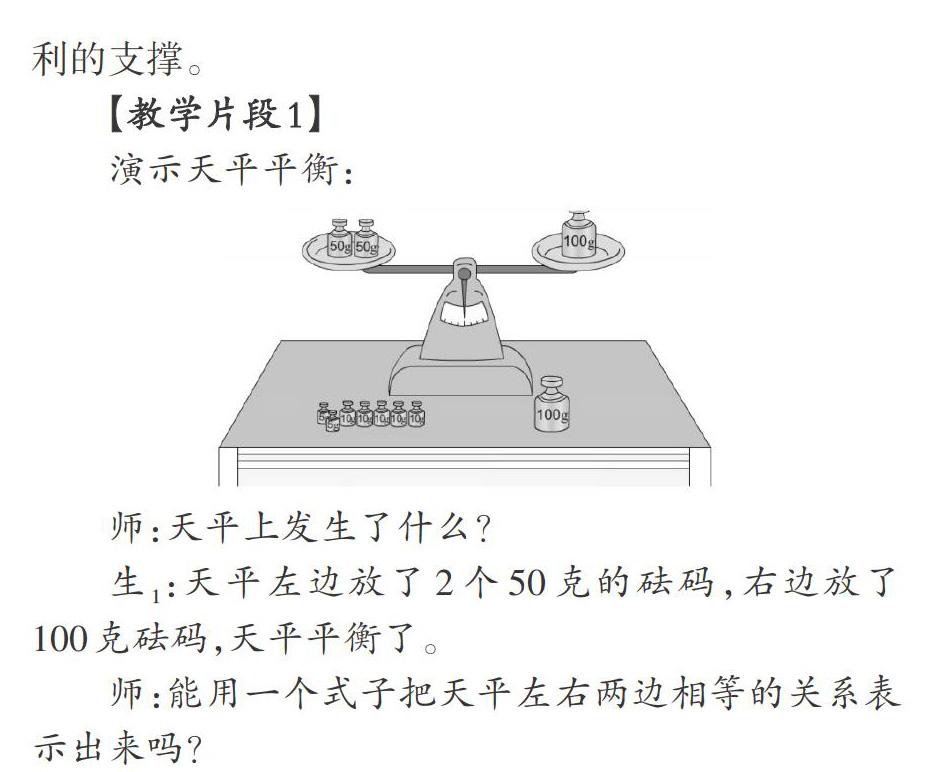
師：天平上發生了什么？

生1：天平左邊放了2個50克的砝碼，右邊放了100克砝碼，天平平衡了。

師：能用一個式子把天平左右兩邊相等的關系表示出來嗎？

生2：50+50=100。

師：誰來說說這個式子的各個部分是怎樣得到的？

生3：左邊是2個50克的砝碼，就是50+50，右邊是100克砝碼，左邊和右邊相等，所以用等號連接。

師：像這樣表示左右兩邊相等的式子就是等式。

師：大家在低年級時就會口算50+50，今天這個50+50=100和口算50+50=100一樣嗎？

生4：不一樣的，今天學習的這個等式是通過天平平衡得到的。

師：對呀，今天學習的這個等式帶給我們不一樣的體驗，它是通過天平兩邊平衡之后得到的。

利用天平平衡讓學生列出等式對五年級學生來說并不是一個難點，因為學生從一年級開始就會用等式表示運算結果。但是今天學習的等式和以前學習的等式內涵一樣嗎？學生對這個概念是模糊的，這就需要利用天平對等式進行全新的學習。學生以前接觸的算式是知道數據和運算符，通過運算得出結果，這就是程序化的思考方式，它是單向的。而這節課認識的等式是結構化的思考方式，它表達的是一種關系和結構，等號兩邊的數學對象是等價的。等式是認識方程的基礎，方程表示的也是一種等價關系，雖然都是等式，但是有本質區別。

三、未知數與已知數“平起平坐”

學生以前學習的都是用已知數通過運算得到未知數，也就是算術的解法，而方程就是在未知數與已知數之間建立起來的等式關系，未知數和已知數一樣參與運算，享受同等的地位，這是算術向代數發展的重大飛躍。在教學中如何體現方程這一核心本質呢？

【教學片段2】

視頻演示天平經過三次調試平衡的過程：

師：一起來看一看找平衡的過程。通過第一幅圖，我們知道了什么？

生1：空杯子的質量是100克。

師：第二、三、四幅圖的意思是什么？

生2：第二幅圖中，空杯子加水之后一定會比100克重;第三幅圖中，右邊加100克砝碼之后，天平的左邊重一些;第四幅圖中，繼續調試，右邊再加100克砝碼，天平右邊又重了，說明這杯水比300克砝碼輕。

師：通過第三幅和第四幅圖，想到什么？

生3：這杯水的質量應該在200克與300克之間。

師：最后一次調試，把右邊的一個100克砝碼換成50克砝碼。經過三次調整，天平終于平衡了。

師：我們已經知道空杯子的質量是100克，可以把它看成已知數，水的質量不知道，那應該怎么辦呢？用x克來表示，能用一個等式把天平左右兩邊相等的關系表示出來嗎？

生4：100+x=250。

師：通常情況下我們用x、y、z來表示未知數。

師：在以前的學習中，未知數不會出現在我們列的算式中。現在它不但出現了，而且和50、100這樣的已知數平起平坐。這標志著我們的學習進入了一個新的階段。

本節課的重點是建模思想，因為它是方程思想的核心。方程的模型就是用等號將相互等價的兩件事情聯系起來，在闡述這個事實中，未知數因勢而生，把它和已知數放到了同等的地位，就要引領學生轉換視角，把未知數看成一個已知條件參與到運算中，這對于學生來說是一種思維的顛覆。

四、“等量關系”不能避而不談

人教版教材 “方程的意義” 中并沒有提到等量關系，那么教學中是否要把等量關系提煉出來呢？構建方程的最重要的環節就是分析具體情境中的數量關系，找出兩件等價的事情后建立等式，也就是數量間的相等關系即等量關系，如果避而不談，弱化等量關系，學生就會憑著感覺走，對方程的認識就會僅僅停留在形式上，不能上升到理性認識，淡化了對方程內涵的理解。學生的關注點只有集中到方程表示的等量關系，對于方程的認識才能達到更高的水平。因此在教學過程中，還是要讓學生找出等量關系，經歷構建方程的過程。

【教學片段3】

視頻演示調試砝碼天平平衡：

學生列出含有未知數的等式：

[杯子的質量+水的質量=砝碼的質量][100+x=250]

師：這個等式表示什么？

生1：天平的左邊表示杯子加水的質量，天平的右邊表示砝碼的質量。

師：這是根據“杯子的質量+水的質量=砝碼的質量”這個等式列出來的。大家不要小瞧了這個相等關系，我們稱它為等量關系。100+x=250這個等式就是根據這個等量關系寫出來的。

師：同桌先說一說，再結合下圖說說這個等式表示的意思，它的等量關系是什么？

在建立方程模型的過程中，一般是先讓學生用自己的語言闡述要解決的問題，然后抽象為數學語言，提煉出等量關系，最后用數學符號建立方程解決問題，建立方程的關鍵就是找出等量關系。學生在這節課上才初識等量關系，教材中提供的具體情境比較簡單，學生又剛剛認識了等式，所以順應學生的思維先列出等式，再讓學生講講等式表達的含義，自然引出等量關系，最后通過練習再次強化等量關系。實踐證明，方程模型的建立不是一蹴而就的，需要一個循序漸進的過程，但是對方程本質的深入認識要貫穿其中。

對方程思想的認識比定義更重要，體會等量關系比技巧訓練更重要。讓學生在具體情境中，經歷建構方程模型、解決問題的過程中，感悟方程的思想內涵，應該是方程教學的價值所在。

（責編 金 鈴）