浮式風機半潛式平臺動力響應研究

張洪建，蔡 新，3，許波峰

（1.河海大學 力學與材料學院，江蘇 南京 211100；2.江蘇省風電機組結構工程研究中心，江蘇 南京210098；3.沿海開發與保護協同創新中心，江蘇 南京 210098；4.河海大學 能源與電氣學院，江蘇 南京211100）

0 引言

海上風能近年來逐漸受到世界各國的重視。浮式風機與傳統固定式風機相比，安裝成本低，成為開發深海風能的首選形式。半潛式風機因其建造成本低、抗風浪能力強等優點，成為了我國浮式風機的主要發展方向。

Yang Yang[1]討論了一種新型多體浮式平臺在有無風浪耦合作用下的運動差異與疲勞載荷。黃致謙[2]設計了一種新型浮式風機半潛平臺，該平臺基于流體力學軟件（AQWA），并結合有限元方法進行數值仿真。范增輝[3]研究了風浪半潛式平臺關鍵部位彎矩的影響，研究表明，相比于塔根底部，橫撐處更易發生破壞。半潛式平臺吃水較淺，平臺重心較高，主要通過系泊系統維持穩定。

本文在OC4-DeepCwind半潛式風機的基礎上，設計了一種具有傾斜立柱的半潛式平臺。基于勢流理論，本文探究半潛式風機在實際海洋環境中的運動特性，并對半潛式平臺結構及系泊系統參數進行了分析優化。

1 風機模型的建立

基于ANSYS建立數值模型，利用AQWA對導入的風機模型進行水動力分析，從而對半潛式浮式風機的動力響應進行數值模擬。

1.1 風力機參數

風機主體采用NREL 5 MW風力機，參數見表1。浮式平臺選用OC4-DeepCwind平臺（以下簡稱原平臺），相關參數見表2[4]。本文設計的一種具有傾斜側柱的新型平臺（簡稱新平臺）參數見表3。

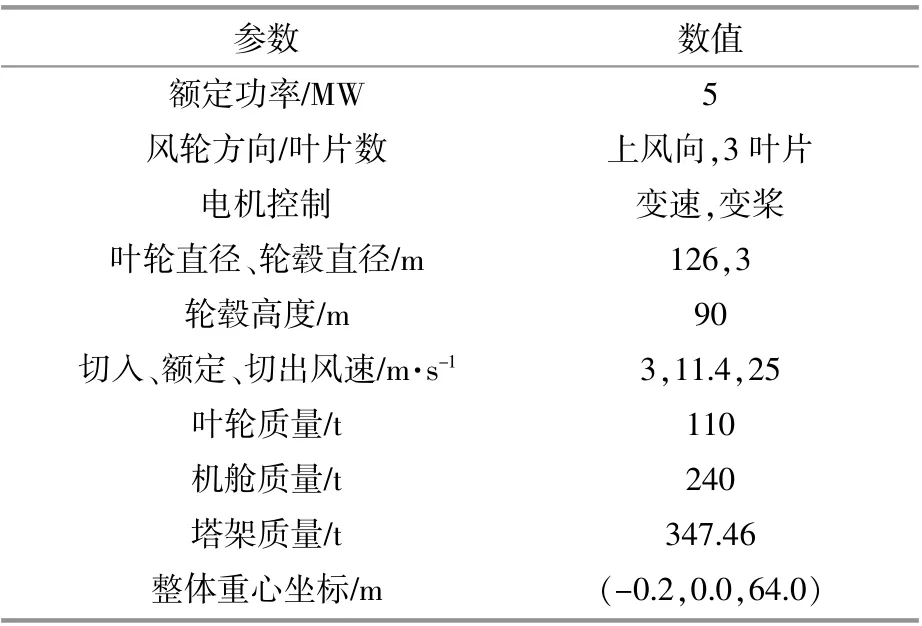
表1 NREL 5 MW風力機參數Table 1 Parameters of NREL 5 MW wind turbine

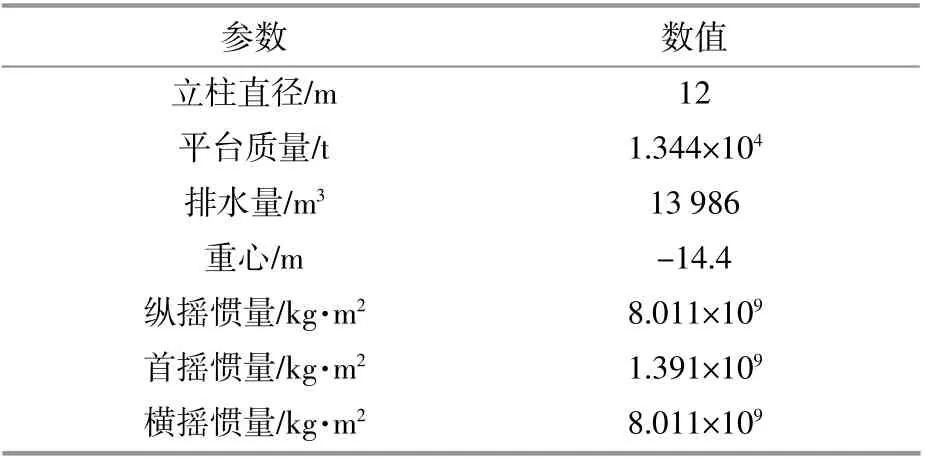
續表2

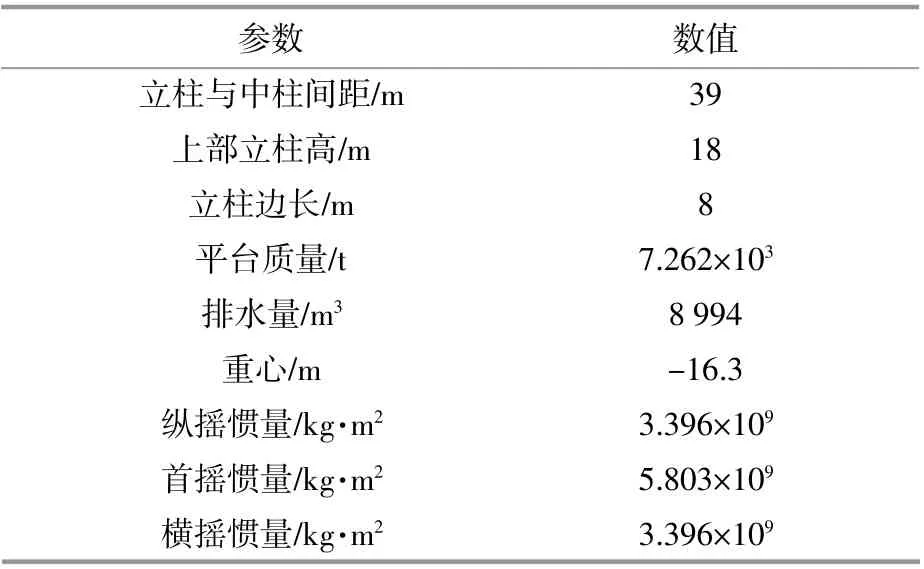
表3 新平臺參數Table 3 Parameters of new platform

1.2 浮式平臺設計

提高浮式平臺穩定性常用的方法為增大平臺質量、立柱間距和水線面積[5]。增大質量會造成制造與安裝成本的增加，直接增加立柱間距將增大支撐部件應力與疲勞載荷，增大水線面積會導致平臺垂蕩周期減小[5]。本文設計的新平臺每個立柱上部直立、下部向外傾斜，使新平臺慣性矩明顯提高，同時支撐構件載荷不會過大。新平臺立柱底部將原平臺的附加質量塊簡化為相同半徑的垂蕩板，大幅降低制造成本，使平臺質量降低了47%，排水體積下降了35.7%。為驗證新平臺的可行性及合理性，將新平臺與原平臺進行對比分析。將塔頂上部結構簡化為集中質量，兩平臺模型如圖1所示。

圖1 浮式風機模型Fig.1 Model of floating wind turbine

2 環境載荷

浮式風機在海洋環境中會受到多種載荷作用，為簡化計算，本文主要考慮風、浪、流3種載荷。

2.1 風載荷

自然界中，湍流風的風速和風向隨時間不斷變化。浮式風機所受的風載荷F為[6]

式中:S為結構的投影面積；Ch，CS分別為高度和形狀系數，取值分別為1.2和0.5[6]；P為風壓。

式中:v為風速。

2.2 波浪載荷

本文研究對象為半潛式平臺，屬于大尺度結構物，其對波浪的影響不可忽略。因此，本文采用勢流理論以求解波浪載荷方程[7]。在勢流理論中，結構物周圍流場總的速度勢為

式中:?I為入射波速度勢；?D為繞射波速度勢；?R為輻射波速度勢。

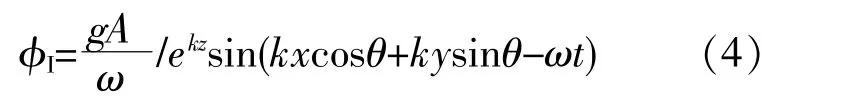
式中:g為重力加速度；A為波浪幅值；ω為波浪頻率；θ為浪向角；k為波數；e為常數。

各個速度勢須滿足Laplace方程和邊界條件。式 中:nj為 物 面 外 法 向 單 位 矢 量，j=1，2，3，4，5，6。

基于上述過程得出了各速度勢和總速度勢，通過Bernoulli方程，求出物體表面的壓力，再沿浮體濕表面積分可求出作用在結構物上的波浪力與力矩。

2.3 流載荷

本文設計水深為200 m，流載荷f為

式中:CD和 ρ分別為拖曳力系數和海水密度，文中CD取值為1；A為結構沿海流方向的投影面積；v為相對流速。

2.4 工況選擇

結構最不利的條件即為風、波和流載荷沿x軸同向施加在平臺上。本文選擇北太平洋實測海況作為研究工況，其環境參數見表4。

表4 環境參數Table 4 Environment parameters

2.5 計算結果驗證

為驗證本文模擬結果的可靠性，將本文譜密度的計算結果與文獻[8]中的試驗數據和FAST數值模擬結果進行對比。圖2為本文譜密度的計算結果與試驗結果和FAST模擬結果的對比曲線圖。由圖2可知:本文與文獻[8]中3個自由度的譜密度變化趨勢基本相同；相較于FAST模擬結果，縱蕩與垂蕩的譜密度更加接近試驗值。但由于試驗尺度效應以及FAST有很多線性化假設，譜密度的具體數值仍然存在差異。根據上述驗證，認為本研究計算結果具備可靠性。

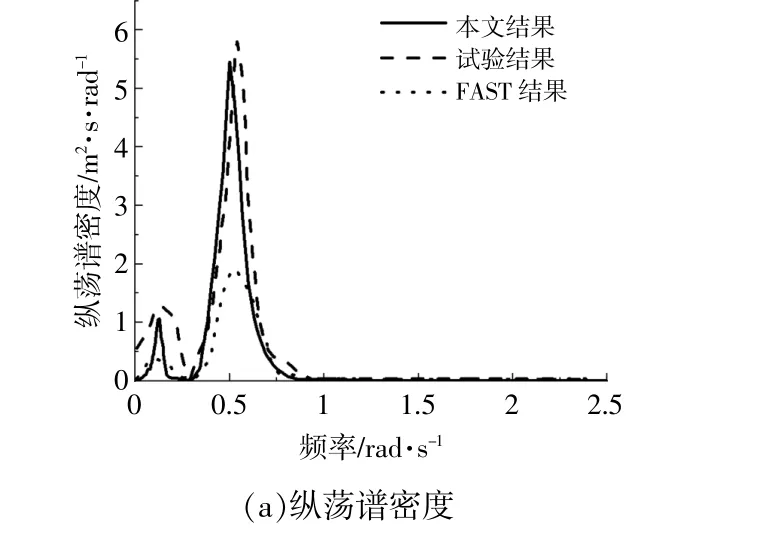
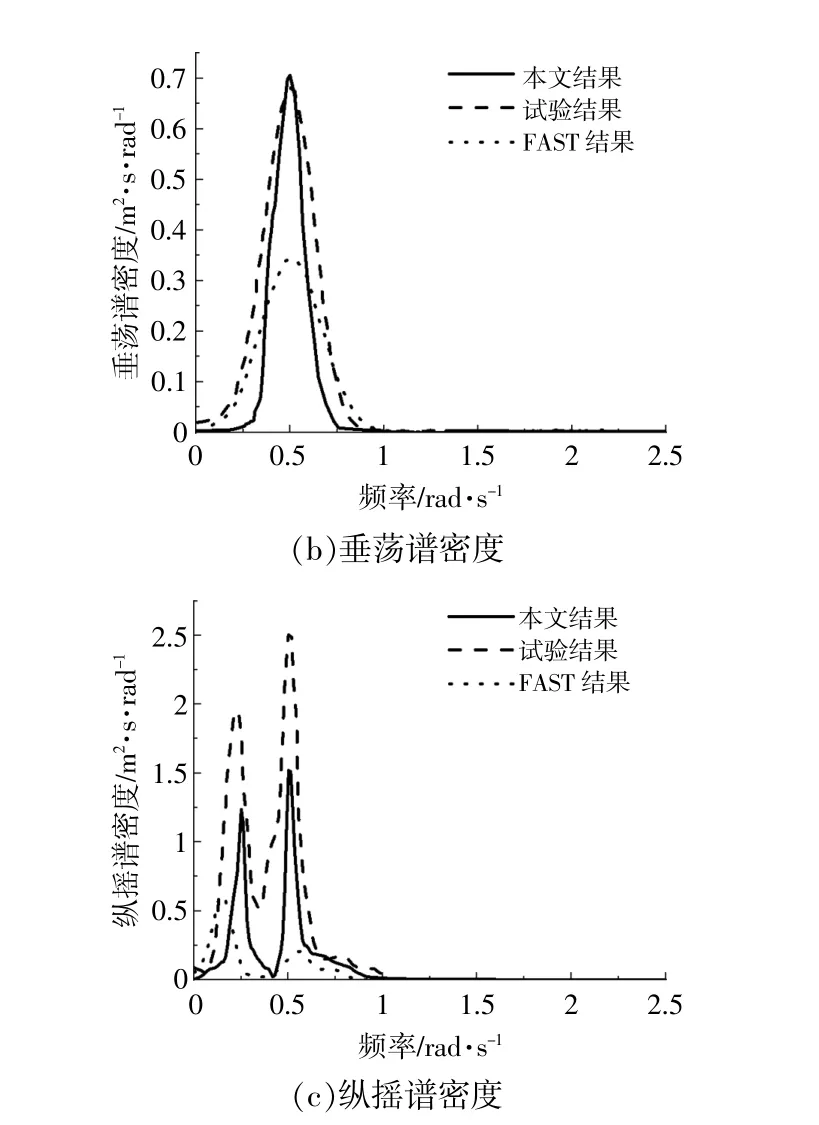
圖2 譜密度計算結果比較Fig.2 Comparison of PSD calculation results

3 頻域與時域分析

3.1 頻域分析

平臺縱蕩、垂蕩及縱搖對浮式風機的穩定性與安全性的影響相對更大。故本文主要從這3個自由度對平臺運動進行分析以及優化。圖3為新平臺與原平臺的3個自由度的RAO變化趨勢。

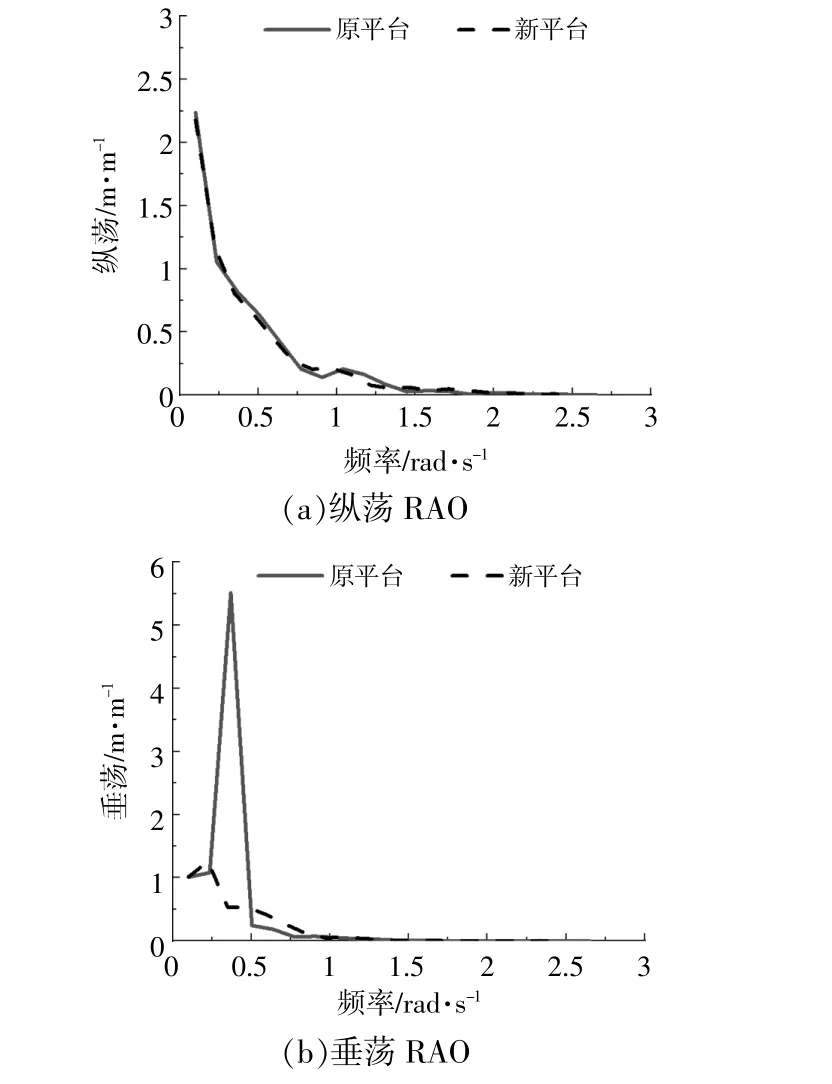
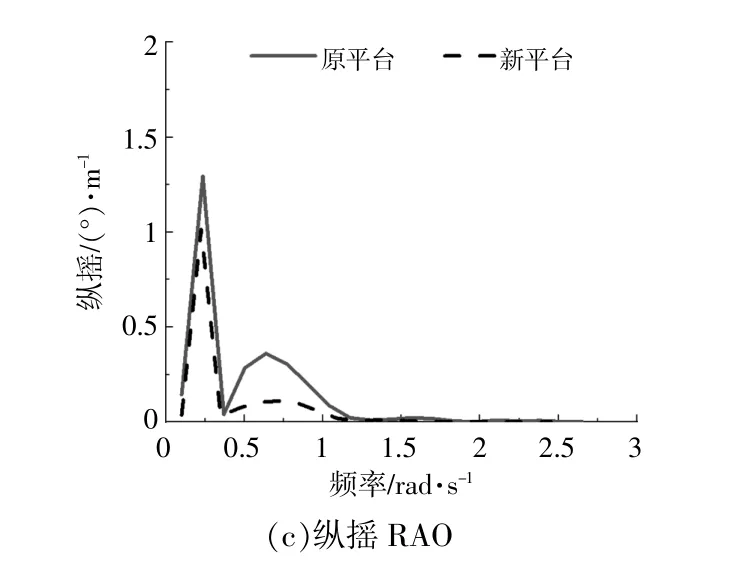
圖3 新平臺與原平臺RAO比較Fig.3 Comparison between the new platform and the original platform RAO

由圖3可知:縱蕩RAO隨頻率的增加而減小；垂蕩RAO隨頻率先增加后減小，最后趨于0；新平臺各自由度運動響應均有降低，縱蕩峰值減少了2.5%，垂蕩峰值降低了77.2%，縱搖峰值減少了18.3%。

為防止結構與波浪發生共振，平臺固有周期應遠離一般波浪周期[9]。一般波浪周期集中在1～30 s內，而對應的能量峰值周期為10 s左右，其波浪譜密度如圖4所示。

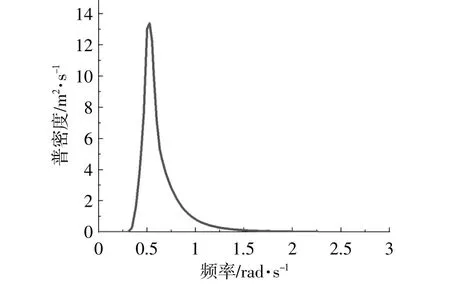
圖4 波浪譜密度Fig.4 Wave spectra density

原平臺和新平臺垂蕩固有周期分別為16.9 s與27.8 s。新平臺垂蕩固有周期遠大于原平臺，可以更有效地預防結構共振的發生。

將波頻處兩種平臺載荷分布云圖進行比較（圖5）。

由圖5可知:兩種平臺接近水面處載荷相對較大，說明波浪載荷對浮式平臺造成很大影響；新平臺最大載荷為44.5 kN/m2，原平臺最大載荷為63.2 kN/m2，新平臺縮小立柱橫截面積明顯降低環境載荷對平臺的影響；新平臺最大載荷僅在單根立柱處分布，而原平臺立柱與中柱均有最大載荷分布，這是由于原平臺各個立柱之間距離較近，相互間水動力影響較強。

圖5 兩種平臺載荷分布Fig.5 Load distribution of two platforms

3.2 時域分析

本節重點研究縱蕩、垂蕩與縱搖運動響應，設定時間為1 000 s，風、浪、流載荷均沿x軸作用于風機。圖6為兩種浮式平臺運動響應時域曲線。

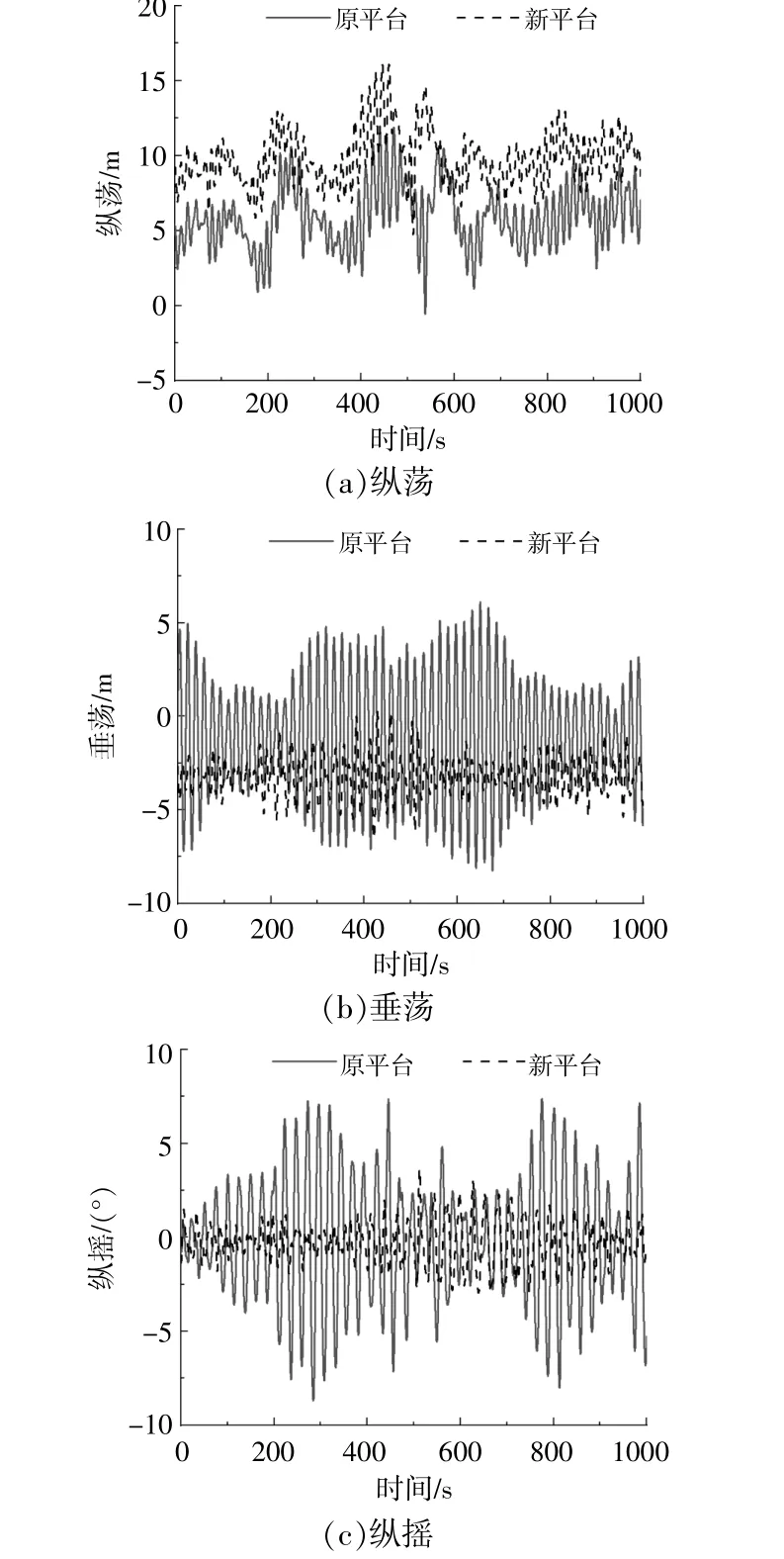
圖6 平臺時域運動響應Fig.6 Time domain of platform motion response

表5為兩種浮式平臺運動響應幅值與平均值。

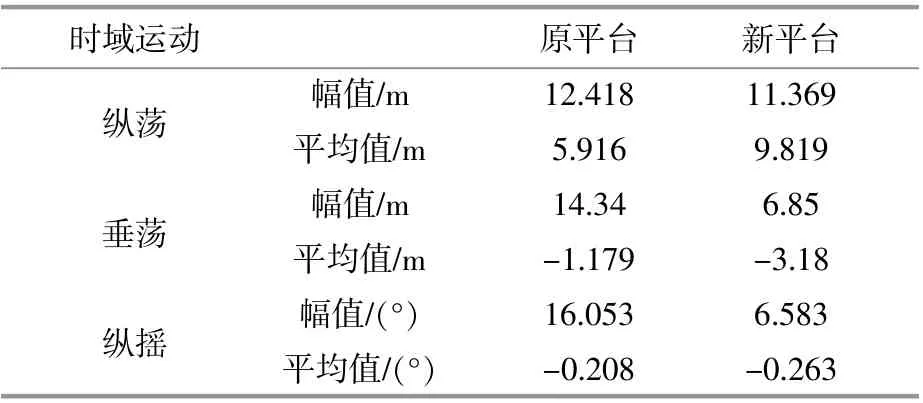
表5 平臺時域運動響應Table 5 Time domain of platform response

根據圖6與表5可知，新平臺縱蕩、垂蕩與縱搖幅值較原平臺分別降低了8.44%，52.23%和59%，垂蕩與縱搖運動響應大幅下降。垂蕩運動響應減小使新平臺避免過多豎向運動而造成的疲勞損傷；縱搖運動響應降低減少平臺多余的俯仰運動，保證了風機的發電效率。

4 系泊系統優化

由前文可知，新平臺縱蕩略大于原平臺，縱蕩過大會導致電纜受到較大載荷而斷裂。因此，須要對新平臺系泊系統進行優化。纜索數量、導纜孔高度和錨點坐標對浮式風機運動響應具有顯著影響。原系泊系統參數見表6。

表6 原系泊系統參數Table 6 Mooring system parameters

4.1 纜索數量優化

設置3組纜索布置形式進行對照，分別為3根纜索、6根纜索（3組，組間纜索夾角為30°）以及9根纜索（3組，組間纜索夾角為15°），具體布置形式如圖7所示。

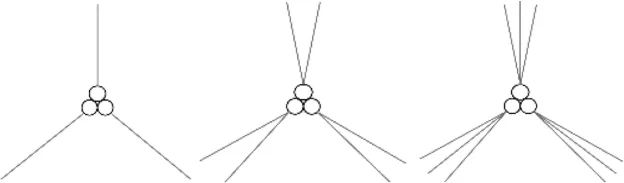
圖7 不同纜索數量布置形式Fig.7 Forms of different cable quantities

圖8為不同纜索數量的新型浮式風機運動響應時域曲線，表7為不同纜索數量的新型浮式風機運動響應統計。

圖8 不同纜索數量時域運動響應Fig.8 Time-domain motion response of different cable quantities

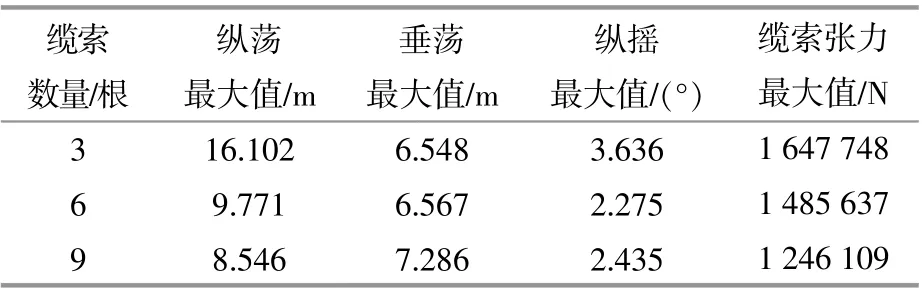
表7 不同纜索數量計算結果Table 7 Calculation results of different cable quantities

由圖8和表7可知:6根纜索相較于3根纜索的縱蕩、垂蕩、縱搖以及最大纜索張力分別下降了39.5%，10.8%，66.5%和4.14%；9根纜索明顯降低纜索張力，但相比于6根纜索縱蕩優化并不明顯，且垂蕩與縱搖最大值反而增加。考慮到實際工程中安全性及經濟性要求，選擇在系泊系統中設置6根纜索。

4.2 導纜孔高度優化

利用響應面算法對導纜孔高度進行參數優化，優化結果與原系泊系統對比結果見表8。

表8 不同連接點高度計算結果Table 8 Calculation results of height of different connection points

由表8可知:導纜孔高度優化后的系泊系統的垂蕩、縱搖和纜索張力最大值分別降低了1.3%，10.5%和5.7%，而縱蕩最大值小幅增加；導纜孔高度對縱搖的影響最為明顯，對縱蕩、垂蕩以及纜索張力影響較小。

4.3 錨點位置優化

基于響應面算法對錨點坐標進行參數優化，優化前后的錨點坐標見表9。同時，將優化后的結果與原系泊系統進行比較（表10）。

表9 優化前后錨點坐標Table 9 Coordinate of fixed points before and after optimization

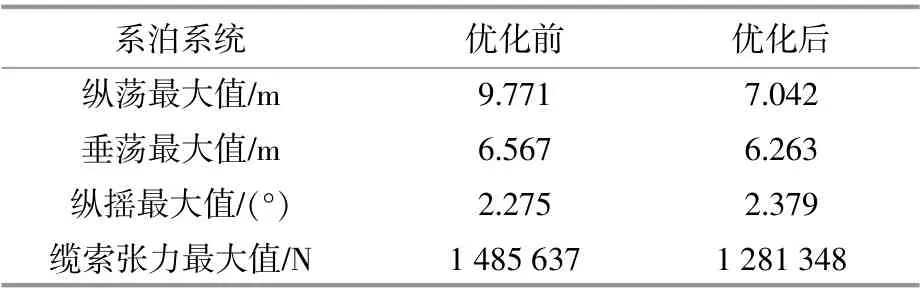
表10 不同錨點位置計算結果Table 10 Calculation results of different fixed points

由表10可知，錨點坐標優化后縱蕩、垂蕩與纜索張力最大值分別下降了27.9%，4.6%和13.8%，而縱搖最大值小幅增加。纜索錨點坐標主要影響縱蕩以及纜索張力。

4.4 系泊系統優化

根據上述得到的最優纜索數量、最優導纜孔高度與最優錨點坐標，提出一種優化的系泊系統，新平臺模型如圖9所示。

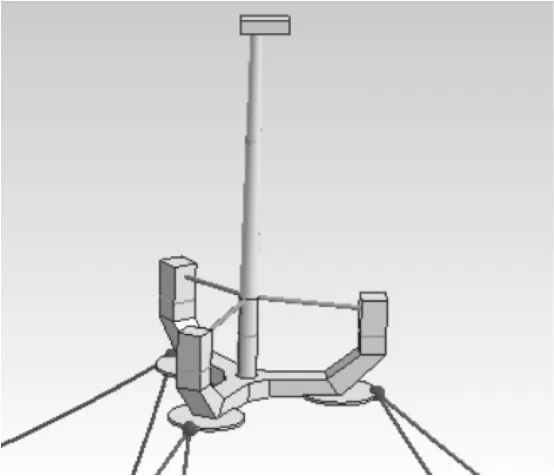
圖9 系泊系統優化后的新平臺模型Fig.9 New platform model after mooring system optimization

優化系泊系統后的新平臺與未優化系泊系統的原平臺的對比結果見表11。由表11可知，系泊系統優化后的新平臺與原平臺相比，縱蕩、垂蕩、縱搖最大值以及纜索張力最大值分別下降了48.7%，5.5%，38.3%和26.2%。采用優化系泊系統的新平臺的運動響應和最大纜索張力均有明顯改善。

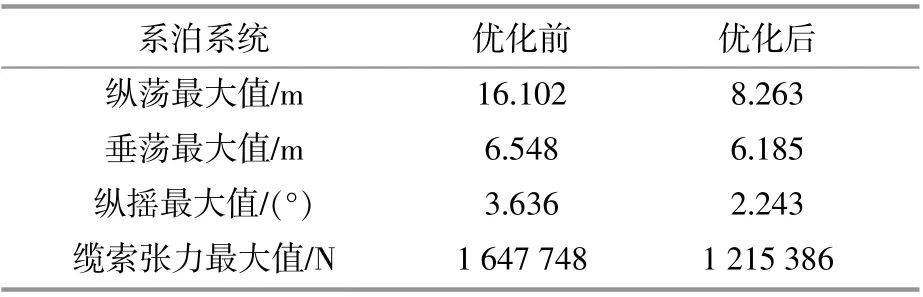
表11 系泊系統優化后的新平臺計算結果Table 11 Calculation results of new platform after mooring system optimization

5 結論

本文在OC4-DeepCwind平臺基礎上，設計一種具有傾斜立柱的新型浮式風機半潛式平臺，并進行了可靠性驗證。基于勢流理論，對兩種平臺進行了頻域與時域分析，對其系泊系統進行了優化，得到以下結論。

①新平臺縱蕩、垂蕩以及縱搖RAO峰值與原平臺相比均有下降，分別降低了2.5%，77.2%和18.3%，新平臺具有更好的防垂蕩與抗傾覆能力。新平臺的垂蕩固有周期增大了64.5%，能夠更大程度防止共振發生。新平臺波頻處的最大表面壓力降低了29.6%，明顯降低了波浪載荷對平臺的影響。

②新平臺縱蕩、垂蕩與縱搖幅值分別降低了8.44%，52.23%和59%，運動響應均較原平臺更加穩定。新平臺也保證了在極端工況下良好的穩定性。

③分別對纜索數量、導纜孔高度與錨點位置進行優化，可以得知導纜孔高度主要影響平臺縱搖，錨點位置主要控制平臺縱蕩與系泊張力，6根纜索更能兼顧安全性與經濟性。優化系泊系統后的新平臺，其運動響應與纜索張力明顯降低，縱蕩、垂蕩、縱搖最大值以及纜索張力最大值分別下降 了48.7%，5.5%，38.3%和26.2%。