基于優化減載與動態慣量控制的DFIG參與系統一次調頻研究

徐 波，彭耀輝，章林煒，邊曉燕，李東東

（上海電力大學 電氣工程學院，上海 200090）

0 引言

大規模風電并網使電網調頻能力下降，影響電網的穩定性[1]，[2]。由于風電機組大多運行在最大功率跟蹤（MPPT）模式下，風電機組與電網解耦運行時，無法響應系統頻率變化[3]。虛擬慣性控制可以有效提高風電機組的調頻能力[4]，[5]，但虛擬慣性控制是利用轉子動能參與系統調頻，過多釋放轉子動能容易使風電機組轉速過低，影響其穩定運行。同時，風電機組調頻能力受其運行狀態影響，波動性較強。

為提高風電機組調頻能力，有關學者提出了超速減載控制策略[6]。文獻[7]采用固定10%減載率并結合虛擬慣性控制，提高了風電機組調頻能力，但固定減載率靈活性較差，高風速時效率較低，且減小了風電機組的有功出力。文獻[8]通過優化算法，根據風速變化動態調整風電機組減載率，具有一定的靈活性，但其減載率選擇的合理性有待驗證。以上文獻減載率的選擇均未考慮系統運行狀態，無法根據系統運行狀態動態調整。

本文提出了一種風電機組優化減載方法。正常運行時，若系統負荷過高，風電機組采用較小減載率，以增大有功輸出。若系統負荷較低，采用較大減載率，以減小有功輸出。系統受到擾動時，根據系統頻率變化動態調整風電機組減載率，調整風電機組有功儲備，參與系統調頻。針對風電機組的慣量水平，本文提出了風電機組動態慣量控制方法，風電機組可以根據其運行狀態動態調整虛擬慣性系數。本文方法能夠根據系統運行狀態動態調整風電機組減載率，提高了其參與系統調頻的靈活性和系統頻率穩定性，還提高了風電機組調頻能力，并能根據風電機組運行狀態適當參與系統調頻。

1 風電機組模型

本文基于雙饋風電機組進行研究。根據空氣動力學模型，風電機組捕獲的風能功率為[9]

式中:Pm為風電機組功率；ρ為空氣密度；Sw為葉片的掃掠面積；CP為風能利用系數；v為風速；λ為葉尖速比；λopt為運行在MPPT模式下的葉尖速比；β為槳距角；ωr為葉片旋轉角速度；R為葉片半徑。

風電機組的搖擺方程為[10]

式中:Hwt為機組等效物理慣性時間常數；Tm為機械轉矩；Te為電磁轉矩。

2 優化減載控制

2.1 系統正常運行時優化減載控制

2.1.1 各風速下減載率優化求取

本文所提控制策略針對中、低風速（v=6～12 m/s）進行研究，超速減載控制在一定程度上能提高風電機組調頻能力[11]，但定減載率控制在實際應用中缺乏高效性與靈活性[12]。目前變減載率大多通過離線計算獲得，在系統運行狀態發生變化時，固定的減載率不再合適。因此，減載率應根據系統運行狀態動態調整。

超速減載控制原理如圖1所示。A點為最大功率跟蹤運行點，B點為在一定減載率下的超速減載運行點。超速減載控制使得風電機組有功輸出減少，但增加了轉子轉速，風電機組旋轉動能增加。

圖1 某風速下超速減載示意圖Fig.1 Over-speed deload control

當風電機組運行在超速減載點（B點）時，風電機組轉子動能增加量為

式中:ωd為待優化求取的超速減載控制下風電機組轉速；ωopt為MPPT模式下風電機組轉速。

設風速采樣時間間隔為T，本文取10 s。假設時間T內風速保持不變，則Popt與Pd均保持不變。在此期間因超速減載造成的發電量損失 ΔEs為

式中:Popt為MPPT模式下風電機組有功輸出；Pd為減載控制下風電機組有功輸出。

將轉子動能增加 ΔEk視為減載控制帶來的收益，而 ΔEs為所需成本。由此可以建立最優化目標函數為

式 中:γk，γs為 權 重 系 數。

為提高風電機組發電率和調頻能力，在中風速 時（v=8～12 m/s），風 電 機 組 調 頻 能 力 較 高，應 盡可能提高其發電率，γk取0.5，γs取0.5。在低風速時（v=6～7 m/s），風 電 機 組 調 頻 能 力 較 弱，發 電 量較少，應盡可能調高其調頻能力，γk取0.7，γs取0.3。風電機組固有物理慣量Jwt，槳葉掃過面積Sw，槳葉半徑R等相關參數可從風電機組參數表中獲得，空氣密度ρ為已知值。

在不同風速下分別求取各優化參數，其約束條件為

本文采用粒子群優化算法對式（7）進行求解。粒子群算法最早由Eberhart和Kennedy在1995年提出，它源于對鳥類覓食行為的研究，模仿鳥類覓食過程進行最優化求解[13]。與遺傳算法相比，粒子群優化算法更高效，使用求解函數數量更少[14]。

通過優化算法可求得風電機組超速減載后的角 速 度 ωd，進 而 通 過 式（1）～（3）可 推 導 出 此 時 有功輸出Pd，則風電機組減載率為

改變風速，重復上述過程，求得不同風速下風電機組最優減載率。風速v和減載率d＇的關系如圖2所示。

圖2 不同風速下減載率Fig.2 Over-speed deload rate at different wind speed

2.1.2 不同負荷水平下風電機組減載率動態調整

傳統變減載控制并不考慮系統負荷情況，靈活性差，發電效率低。本文考慮了系統負荷情況，優化調整風電機組減載率。系統負荷較小時采取高減載率，從而減小風電機組出力、增加有功備用；而負荷較大時采用低減載率，從而增加有功輸出。

目前，系統負荷情況可以通過負荷預測方法獲得[15]。假設通過負荷預測得到日負荷曲線中未來某一時刻系統瞬時負荷為PL，該日平均負荷為Pav，定義系統負荷比為

考慮系統負荷時，風電機組減載率為

綜合考慮風電機組運行狀態和系統負荷情況，確定風電機組減載率的流程如圖3所示。

圖3 不同風速下減載率取值流程圖Fig.3 De-load rate calculation flow chart

由圖3可知，通過考慮系統實時負荷水平，動態調整風電機組減載率，既增強了風電機組調頻能力，又提高了發電效率。

2.2 系統受到擾動后減載率動態調整方法

當系統受到擾動后，傳統虛擬慣性控制利用風電機組轉子動能，進行短時間的頻率調整，但過多地釋放轉子動能容易使風電機組過度響應，影響其穩定運行[3]。系統受到擾動后，本文所提方法通過動態調整 λ值，以改變風電機組減載率。進而調整有功儲備，使風電機組參與系統一次調頻，為系統提供較長時間尺度的有功支撐。

根 據 式（1）～（4）可 以 推 導 出 減 載 率d與 葉 尖速比 λ之間的關系。進而，由圖2可得葉尖速比 λ與風速v間關系。

系統受到擾動后，葉尖速比動態調整為

式中:λd為減載控制下風電機組葉尖速比，其隨風速與系統負荷變化，經過每次采樣不斷更新；Δλ為隨系統頻率變化而動態調整的葉尖速比。

頻率偏差與葉尖速比偏差間關系為式中:λopt為MPPT模式下葉尖速比，通常為8.1；Δfmax為系統安全運行范圍內允許的最大頻率偏差，系 統 容 量 較 小 時，Δfmax=±0.5 Hz[16]。

系統受到擾動后，減載率動態調整過程中風電機組有功與轉速變化如圖4所示。

圖4 減載率動態調整過程Fig.4 Dynamic adjustment process of load shedding rate

由圖4可知，當系統負荷增加導致頻率下降時，頻率調整為A→A＇→A的過程。A→A＇過程中 λ值減小，從而減載率降低，增大了風電機組有功輸出。同理，當系統負荷減小時頻率調整為A→A″→A的過程。

3 風電機組動態慣量控制

通過控制葉尖速比調整風電機組減載率，為系統提供較長時間的有功支撐，并且不會出現風電機組過度響應現象。但擾動初期頻率偏差往往較小，無法提供較大的有功支撐，未能充分發揮其調頻能力。因此，還須要動態慣量控制相配合，共同響應系統頻率變化。

根據式（4）可以推導出虛擬慣量控制在單位時間內，風電機組旋轉動能變化量為

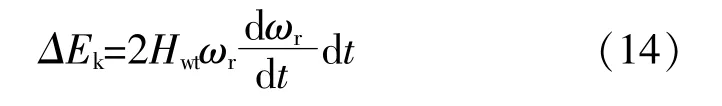
式中:ωr為風電機組旋轉角速度。

在虛擬慣量控制過程中可以近似認為，風電機組動能變化量全部轉化為系統電能。即:

把 式（14）代 入 式（15），兩 邊 同 時 積 分 可 得 虛擬慣性系數Kinertia與風電機組固有慣性時間常數間關系為

優化變減載率和動態慣量控制原理如圖5所示。

圖5 優化變減載率和動態慣量控制原理圖Fig.5 Optimized load shedding and dynamic inertia control

4 仿真驗證

在Matlab/Simulink中搭建兩區域電力系統，如圖6所示。區域1含有由310臺1.5 MW雙饋式風力發電機組成的風電場和900 MW同步發電機G2。區域2含有兩臺900 MW同步發電機G3，G4。所有風電機組的減載率均按照前文提出的方法設置，并參與系統一次調頻。t=50 s時，在區域間設置負荷擾動為LD=300 MW。

圖6 兩區域仿真系統Fig.6 Two areas simulation system

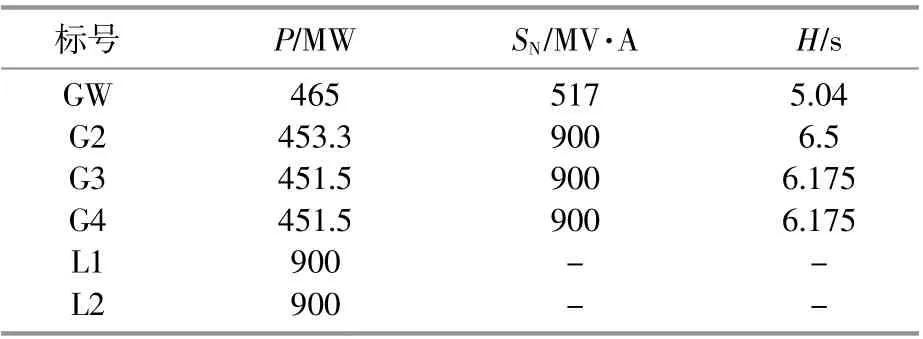
表1 仿真主要參數Table 1 Simulation parameters

為了驗證本文的控制方法，分別考慮不同負荷、不同風速工況。同時，將本文所提控制方法（ODRIC）與以下3種控制策略進行了對比分析。①策略A為無減載控制，無虛擬慣性控制；②策略B為無減載控制，傳統虛擬慣性控制；③策略C為10%定減載控制，優化、自適應系數控制[17]。

虛擬慣性控制原理如圖7所示[18]。本文KH=15，KD=20。

圖7 傳統虛擬慣性控制原理圖Fig.7 Traditional virtual inertia control

4.1 不同負荷下仿真驗證

本文提出的控制方法先優化求取各風速下最優減載率；再根據系統負荷情況，調整風電機組的減載率，使減載率能夠隨系統負荷靈活變化，進而提高其調頻能力和發電效率。分別在系統輕載與重載兩種工況下進行仿真分析。

4.1.1 系統輕載時

仿真設置風速固定為10 m/s，按式（10）設置l為94%。仿真并記錄數據。輕載時系統頻率、風電機組出力和轉速變化如圖8所示。由圖8可以看出，正常運行時，由于此時系統負荷水平較低，本文方法ODRIC通過提高風電機組減載率，既提高了風電機組轉速與有功備用，又減小了系統頻率偏差。在系統輕載時，在ODRIC控制下，風電機組具有更高的減載率，因此具有更高的調頻能力。t=50 s時系統受到擾動，ODRIC能根據風電機組運行狀態，動態調整風電機組減載率和虛擬慣性系數，提供更多的有功支撐，系統具有更小的頻率偏差。

圖8 風速為10 m/s，l=94%時仿真結果Fig.8 Simulation results at wind speed 10 m/s,l=94%

4.1.2 系統重載時

調整系統負荷比l=106%，保持風速與擾動大小不變。同樣可以得到系統頻率、風電機組出力和轉速變化如圖9所示。

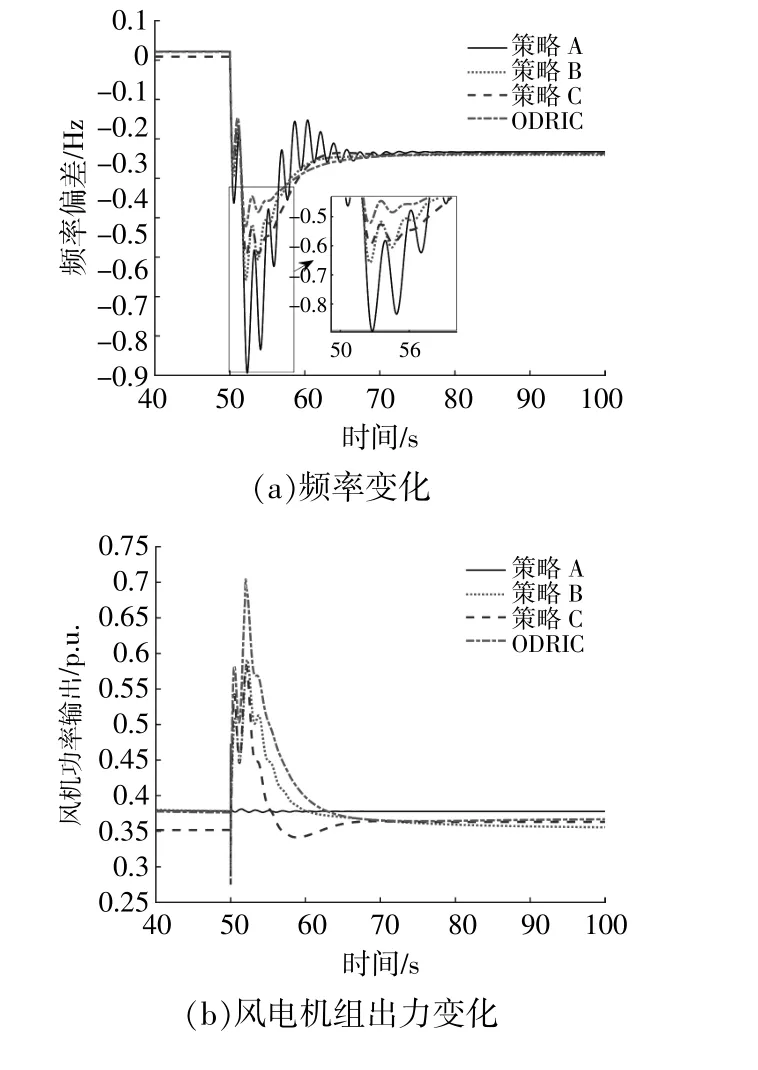
圖9 風速為10 m/s，l=106%時仿真結果Fig.9 Simulation results at wind speed 10 m/s,l=106%

由圖9可知，正常運行時，由于系統重載，本文方法ODRIC將采取較小的減載率，增大風電機組有功輸出。此時，相比其他控制策略，ODRIC使系統具有最小的頻率偏差。在ODRIC控制下，風電機組轉速較高，具有較高的調頻能力。在系統受到擾動后，ODRIC能夠充分釋放風電機組存儲的有功，減小頻率偏差。

4.2 不同風速下仿真驗證

不同風速下，風電機組調頻能力不同。為了驗證在不同風速下，本文所提控制方法的有效性和優越性，仿真分別采用中風速（10 m/s）和低風速（7 m/s）兩種情況進行驗證。

4.2.1 中風速時

設置風速為10 m/s，l=100%。擾動大小保持不變，仿真結果如圖10所示。

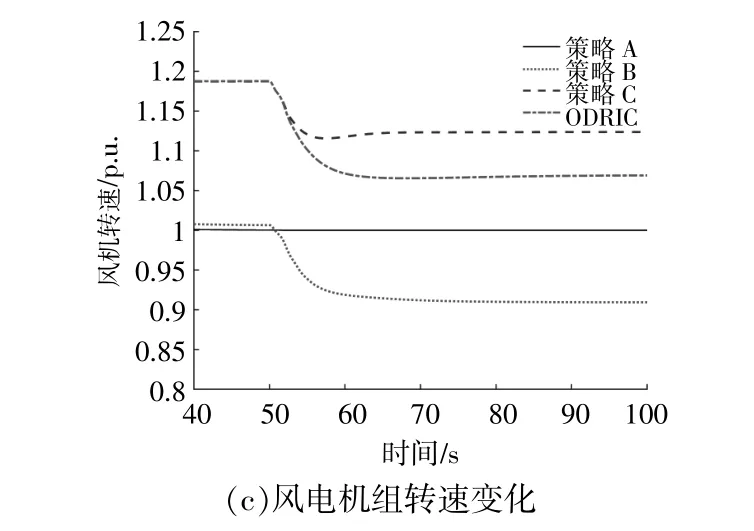
圖10 風速為10 m/s，l=100%時仿真結果Fig.10 Simulation results at wind speed 10 m/s,l=100%

由圖10可以看出，本文方法可以根據風電機組運行狀態充分地發揮風電機組調頻能力，頻率波動小，使系統具有更小的故障率以及頻率偏差。

4.2.2 低風速時

設置風速為7 m/s，l=100%。擾動大小保持不變，仿真結果如圖11所示。

圖11 風速為7 m/s，系統l=100%時仿真結果Fig.11 Simulation results at wind speed 7 m/s,l=100%

由圖11可知，當風電機組運行在低風速時，其轉速較慢，調頻能力較低。由于策略B采用固定調頻系數，過度響應頻率變化。在系統受到擾動數秒后，出現負的有功支撐，極易引起頻率的二次跌落，威脅系統頻率穩定。策略C為保證風電機組穩定運行，優化調整風電機組調頻系數。這種方法過于保守，風電機組提供的有功支撐過低，反而增加了系統頻率偏差。

ODRIC在低風速時具有較高的減載率，使風電機組運行在較高轉速下。同時，系統受到擾動后，通過適度釋放轉子動能，風電機組能夠平滑、連續地提供有功支撐。

5 結論

本文提出了一種風電機組優化減載與動態慣量控制方法。該方法能動態調整風電機組減載率，可以根據風電機組轉速動態調整動態慣量。與傳統虛擬慣性控制方法相比，本文方法可以有效防止風電機組調頻過程中過度響應，有效防止頻率的二次跌落。最后，通過不同風速、負荷水平等工況下的仿真表明:系統正常運行時，本文方法能根據系統負荷水平和風速動態調整風電機組減載率。提高了風電機組調頻能力，又減小了系統頻率偏差。擾動發生后，本文方法能夠根據風電機組運行狀態，動態調整風電機組減載率與動態慣量控制系數。保證風電機組穩定運行的同時，為系統提供更大、更持久的有功支撐。