一道高考題引發的思考與研究
趙愛華
(新疆烏魯木齊市教育研究中心 830002)
近年來,在各種重要考試中經常出現以2011年全國Ⅱ卷理科第16題為母版的試題,呈現形式多樣,選擇題、填空題、解答題均有考查,但是歷屆學生答題準確率都較低,這引起了我們的關注,并在實踐中開展了深入的探究.
一、題目呈現

二、總體分析
一般認為,本題以正弦定理為入口,考查三角函數的性質.但是命題專家在“結論AB+2BC”中的“2”上做了文章,將問題變得撲朔迷離.很多學生在最后的出口上會遇到困難.因此,必須另辟蹊徑,突破難點.既然題目在求最值的出口處設置了障礙,那么我們必須以不同的視角來研究此題,找到突破口.事實上,本題遠不止一個入口.它蘊含了豐富的教學素材,留給了教師、學生廣闊的思維空間.此模型備受專家的青睞,編制了很多翻新試題.
三、本質探究

四、解法探究
視角1 從正弦定理入手,依托三角函數性質作答.


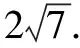
評析本解法中,部分功底不扎實的學生會對(*)處有疑惑,φ究竟有多大?C+φ能取90°嗎?導致解題失敗.事實上,由正切函數的單調性知30°<φ<45°.從幾何角度或三角形內角和可以發現0° 視角2從余弦定理入手,利用判別式作答. 即3=c2+a2-ac. 令t=c+2a.① 即c=t-2a.② 將②代入①整理,得7a2-5ta+t2-3=0. 于是Δ=(-5t)2-28(t2-3)≥0. 評析本解法用整體處理的技巧,從二次方程的角度,構造了以目標函數為參數,邊長a為變量的二次方程,自然避開了角對問題的干擾. 視角3 從余弦定理入手,利用三角換元作答. 評析本解法恰當利用了題設轉化而得的平方關系式,借助sin2θ+cos2θ=1消元,構造自變量不受限的三角函數,解法干凈利落. 視角4 從余弦定理入手,利用極坐標作答. 解法4由解法2知,3=c2+a2-ac. 令c=ρcosθ,a=ρsinθ,代入3=c2+a2-ac,得ρ2(cos2θ+sin2θ-sinθcosθ)=3. 于是c+2a=ρ(cosθ+2sinθ) 整理,得(z-4)t2-(z+4)t+z-1=0. 于是Δ=[-(z+4)]2-4(z-4)(z-1)≥0. 評析本解法恰當應用了極坐標的極徑和角度互化功能,實現了極徑化極角,將問題等價轉化.多次函數轉化,將難點一步一步攻克,充分體現了等價轉化的數學思想的重要性. 本題無論從正弦定理入手,還是從余弦定理入手,均可以順利解答.我們可否認為兩個定理是等價呢?答案是肯定的,下面證明之. 在ΔABC中,A,B,C所對邊分別為a,b,c.R為ΔABC外接圓半徑. 首先用余弦定理來推導正弦定理: 因為sin2A=1-cos2A 同理可得 其次用正弦定理來推導余弦定理: 由正弦定理知a=2RsinA,b=2RsinB,c=2RsinC, =sinBsinC-cosBcosC =-cos(B+C) =cosA. 這就是余弦定理的一個表達式,同理可推導另外兩個表達式.至此,我們證明了正余弦定理的等價性.在平常解題中,我們只是為了解題方便,運算簡單,在二者之間進行了選擇,理論上二者在功能上沒有本質區別. 變式1 若實數x,y滿足x2+y2-xy=3,則x+y的最大值是 ____. 說明這種變式降低了難度,應用解法1這種通解通法處理目標函數時,能夠準確找到輔助角公式的φ,因為此時的輔助角φ為特殊角,學生能恰當處理. 變式2 若實數x,y滿足x2+y2+xy=3,則x+y的最大值是 ____. 說明這種變式相當于將原題的角B換成了120°,目標函數沒有設置障礙,訓練學生舉一反三的能力. 變式3 若實數x,y滿足x2+y2-xy=3,則2x+y的最大值是 ____. 說明這種變式與原題是等價命題,系數2移動位置,不影響問題的本質與難度,恰好能體現三角形的邊AB,BC的對等性. 變式4 若實數x,y滿足x2+y2-xy=3,則2x+3y的最大值是 ____. 說明這種變式與原題也是等價命題,目標函數中系數2,3增加了問題的迷惑性,但不影響問題的本質. 說明這種變式改變了目標函數的類型,恰好能引導我們使用三角換元作答,當然別的解法也可以解答,只是沒那么快捷. 變式6 若x2+2xy+2y2=6,則z=x2+4y2的取值范圍為____. 說明這種變式改變了非線性可行域和目標函數的類別,但不影響問題的最值是曲線與直線相切造成的這一本質屬性.利用判別式、三角換元均可順利作答. 從而z=x2+4y2 由-1≤sin(2θ+φ)≤1, 高考題教學的第一層次是講清楚題目本身,第二層次講清楚題目后進行變式訓練,第三層次是上升到“揭示問題本質”,這種“破繭化蝶”的心路蛻變歷程,過程艱難但結果美麗,對老師和學生都大有裨益. 開展深度教學勢在必行.這類問題極容易停留在解法1的認識層次上.不思索就不會全面認識問題的深刻內涵,更談不上培養學生的高階思維.我們有沒有對問題中的系數2產生疑問呢?是否揣摩了命題者的意圖呢?這些活動都能提升學生的數學思維品質.深度教學的發生離不開教學的組織與引導.我們必須克服教學過程中表面、表層、表演的局限,引導學生深層、深刻、深度學習.經歷從理論到實踐的一整套思維方式和行為模式的轉化,深度教學才能促進深度學習真實發生,才能克服同類問題反復做反復錯的現象. “授之以魚,不如授之以漁”,在數學教學過程中,我們要擅于總結同類問題的共性,找到此類問題的解決策略,低起點,小步子,借助問題的不斷變式,逐步提升問題的難度,授予學生方法,讓學生做一道會一類,這樣我們才能做到課堂教學高效率,學生學習高成效.教學難點才能真正被突破.
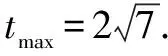
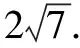




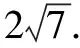


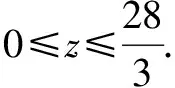

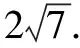
五、一點思考




六、變式訓練



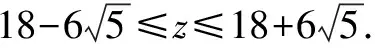



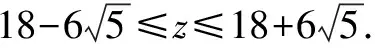
七、教后反思

