羅 錕，汪振國

(1.華東交通大學 鐵路環境振動與噪聲教育部工程研究中心，南昌 330013；2.大連理工大學 土木工程學院，遼寧 大連 116024)

在建筑結構、交通運輸、工程機械等諸多領域，噪聲污染問題一直受到廣泛關注[1]，研究準確有效的聲學數值計算方法是噪聲預測和控制技術發展的基礎，也是解決噪聲污染問題的關鍵步驟。當前，已有許多成熟的數值計算方法在聲學領域得到應用，例如：有限元法[2-3]、邊界元法[4-5]、統計能量法[6-7]、多方法聯合求解[8-10]等。然而，適于描述復雜動力系統的元胞自動機(cellular automata，CA)方法在聲學系統的建模和計算方面卻鮮有應用。

CA自其誕生至今，已衍生出幾種獨立在CA模型之外的計算模型，如格子氣自動機(lattice gas automata，LGA)模型、格子Boltzmann模型、多粒子模型等，且在各種物理問題的建模上均有應用[11]。在模擬波傳播方面：Leamy[12]介紹了一種在理想化線彈性介質中利用Moore型鄰居CA方法模擬地震波的傳播行為；Nishawala等[13]結合毗域動力學與CA方法對彈性波傳播進行模擬，結果顯示CA計算值與解析解吻合較好；Krutar等[14-15]利用LGA模型模擬了波浪現象，并探討了復雜場景下水中聲傳播和散射問題；Sudo等[16-17]在此基礎上，進一步改進LGA模型，提出聲傳播的一維和二維LGA模型，其中二維聲傳播模型雖求解穩定，但計算結果存在各向異性色散；Komatsuzaki等[18]利用CA模型模擬了一維和二維聲傳播現象，其中二維CA模型采用Von Neumann型鄰居，這導致元胞狀態變量在每一計算步中出現各向異性更新的問題，從而二維CA計算結果與解析解間存在較大差異。可以發現，若要應用CA方法對聲學問題進行準確求解，則必須解決元胞各向異性更新的問題。

本文首先應用CA原理，結合聲波方程導出一維聲學CA模型的局部演化規則，并對聲管聲場進行建模，同時考慮兩種邊界條件，利用一維CA模型計算管內聲壓分布，并將結果與解析解進行對比驗證；之后，以脈動球源聲場為分析對象，按球坐標下的二維聲波方程導出Y函數一維CA模型的局部演化規則，進而利用Y值與聲壓值間的關系建立二維脈動球源聲場的CA模型，并計算球源聲輻射性質；最后對比分析二維CA結果與解析解。

1 CA理論及其聲學模擬

CA是一種離散化的動力系統，其由元胞、元胞空間、鄰居、狀態變量、局部演化規則和邊界條件等部分組成[19]，如圖1所示。

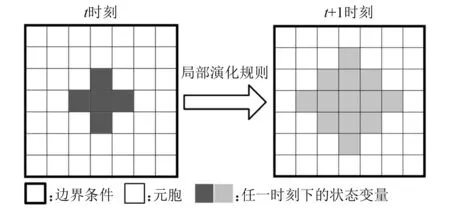
圖1 元胞自動機系統Fig.1 Cellular automata system

對于某一具體問題，應用CA方法往往需要將計算區域在時間和空間上進行離散，每一離散單元稱為元胞或元胞單元，所有元胞組成的集合就是元胞空間；狀態變量通常為需求解的數或數集，每一個元胞內都對應著狀態變量，且在不同時刻下實時更新；對于一個元胞來說，其周圍相鄰的且在單位時間步內參與演化的元胞為其鄰居，如圖2所示。一維CA系統鄰居通常以半徑R為認定準則，即在半徑R以內的元胞均為該元胞的鄰居，二維CA系統鄰居類型多樣，其中Von Neumann型與Moore型最為常見；CA系統的邊界條件按所求解問題的實際邊界條件進行模擬。

圖2 CA系統鄰居類型Fig.2 Neighbor types of CA system

局部演化規則是CA系統中最為重要的組成部分，它能夠由當前時刻元胞及其鄰居的狀態變量確定出下一時刻元胞的狀態變量，簡單來講，局部演化規則就是一組狀態轉移函數，其表達式為

(1)

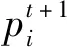
應用CA方法求解聲學問題的一般步驟是：首先需分析聲源及其輻射聲場特性，明確聲學CA模型的維度和鄰居類型；之后對計算區域進行元胞單元劃分，并確定元胞尺寸和時間步長，同時以聲壓為狀態變量，考慮輻射聲場的聲學邊界條件，并按聲波方程導出局部演化規則；最后構建聲學CA模型進行求解。

2 一維聲學CA模型

2.1 局部演化規則

聲傳播的一維聲波方程為

(2)

式中：p為x，t的聲壓函數；c為聲速。

定義元胞單元尺寸為Δx，時間步為Δt，在任意t時刻，式(2)的差分形式為

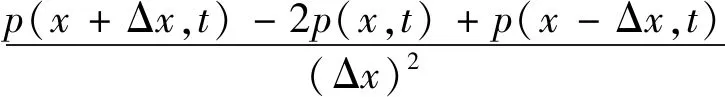
(3)

定義局部演化系數

φ=(c·Δt/Δx)2

(4)

將式(4)代入式(3)并化簡可得

p(x,t+Δt)=φ{p(x+Δx,t)+p(x-Δx,t)+[(2/φ)-2]p(x,t)-(1/φ)p(x,t-Δt)}

(5)

從式(5)可以看出：x位置處元胞t+Δt時刻的聲壓值與其左、右兩相鄰位置x+Δx，x-Δx元胞t時刻聲壓和該元胞t-Δt時刻聲壓相關，因此鄰居類型為R=1型，如圖3所示。同時，因為CA模型中聲傳播速度ca等于聲速c，所以局部演化系數

圖3 一維聲學CA模型鄰居Fig.3 Neighbors of 1D acoustic CA model

φ=(c·Δt/Δx)2=(c/ca)2=1

(6)

那么式(5)可進一步簡化為

p(x,t+Δt)=p(x+Δx,t)+p(x-Δx,t)-p(x,t-Δt)

(7)

式(7)即為一維聲學CA模型的局部演化規則。

2.2 管道聲學CA模擬

設有l=2 m長聲管，管體為剛性壁，其法向振速為0，入射壓力波與管道平行，管內聲波以平面波的形式傳播，在傳播過程中不發生徑向粒子的振動，所以管內聲場可由一維CA模型模擬，如圖4所示。通過考慮兩種邊界條件來確定管中聲壓分布規律：①左端激勵，右端開口；②左端激勵，右端剛壁。

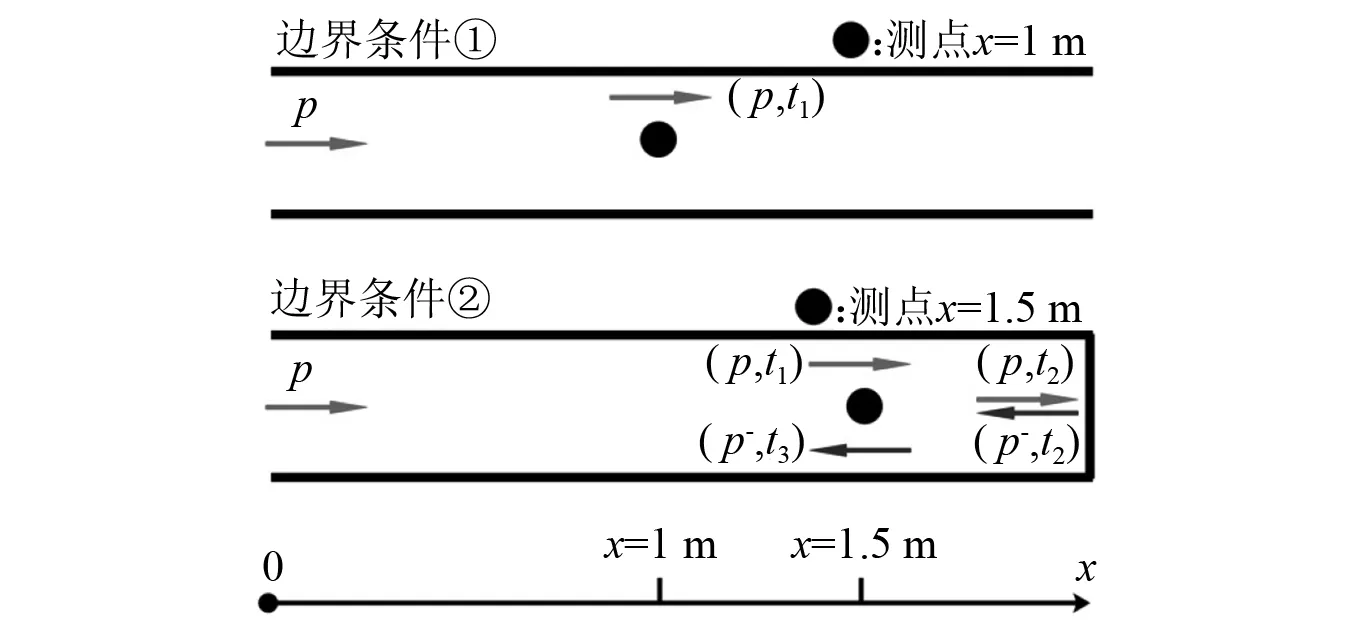
圖4 聲管邊界條件Fig.4 Boundary conditions of acoustic tube

在邊界條件①的聲管中，選擇x=1 m處為測點，入射聲波p在t1時刻到達該位置，則該測點聲壓解析解的表達式為

p(x,t)=p0ei(ωt-kx+θ)

(8)

式中：p0為聲壓幅值；ω為圓頻率；k為波數；θ為位相。

在邊界條件②的聲管中，選擇x=1.5 m處為測點，入射聲波p在t1時刻到達該位置，在t2時刻到達末端剛壁并發生反射，形成沿-x向的反射聲波p-，p-在t3時刻到達測點處，此時開始，測點將處于p與p-的合成聲場中。該測點聲壓解析解的表達式為

(9)

將管內聲場沿x向離散成單元尺寸Δx=1 mm的元胞，以式(7)為局部演化規則，建立一維聲學CA模型，對兩種邊界條件下管內聲場聲壓進行求解，將計算結果與解析解對比，如圖5所示。計算參數如表1所示。

圖5 聲管測點聲壓時程曲線Fig.5 Sound pressure time history curve of measuring points in acoustic tube

表1 計算參數Tab.1 Calculation parameters

由圖5可知：兩種邊界條件下的CA模型計算結果與解析解吻合良好，單向平面波場最大誤差僅為0.614%，合成平面波場最大峰值誤差為1.048%，這表明聲學CA模型能夠準確模擬平面波場聲壓分布，且計算結果可靠。

在邊界條件②下，聲管的共振頻率f為

f=mc/2l

(10)

式中：m為階數，m=1,2,…；c為聲速；l為管長；當入射聲波頻率為前3階共振頻率時，管內聲壓分布，如圖6所示。

從圖6可知：聲學CA模型能夠模擬聲共振現象，當在自然頻率附近激發正弦波時，合成聲場會出現駐波，圖5(b)中合成波幅值不等于10 Pa，這是因為入射波頻率為2 000 Hz，介于共振頻率第23階(1 972.25 Hz)～第24階(2 058.25 Hz)。

圖6 聲模態Fig.6 Acoustic modes

3 二維聲學CA模型

3.1 Von Neumann型CA局部演化規則

聲傳播的二維聲波方程為

(11)

式中：p為x，y，t的聲壓函數；c為聲速。

定義元胞單元尺寸為Δx=Δy=Δl，時間步為Δt，局部演化系數φ=(c·Δt/Δl)2，在任意t時刻，式(11)的差分形式可變化為

p(x,y,t+Δt)=φ{p(x+Δx,y,t)+p(x-Δx,y,t)+
p(x,y+Δy,t)+p(x,y-Δy,t)+

2[(1/φ)-2]p(x,y,t)-(1/φ)p(x,y,t-Δt)}

(12)

從式(12)可知：(x，y)位置處元胞t+Δt時刻的聲壓值與其上、下、左、右4處相鄰位置(x，y+Δy)，(x，y-Δy)，(x-Δx，y)，(x+Δx，y)的元胞t時刻聲壓和該元胞t-Δt時刻聲壓相關，因此鄰居類型為Von Neumann型，如圖7所示。

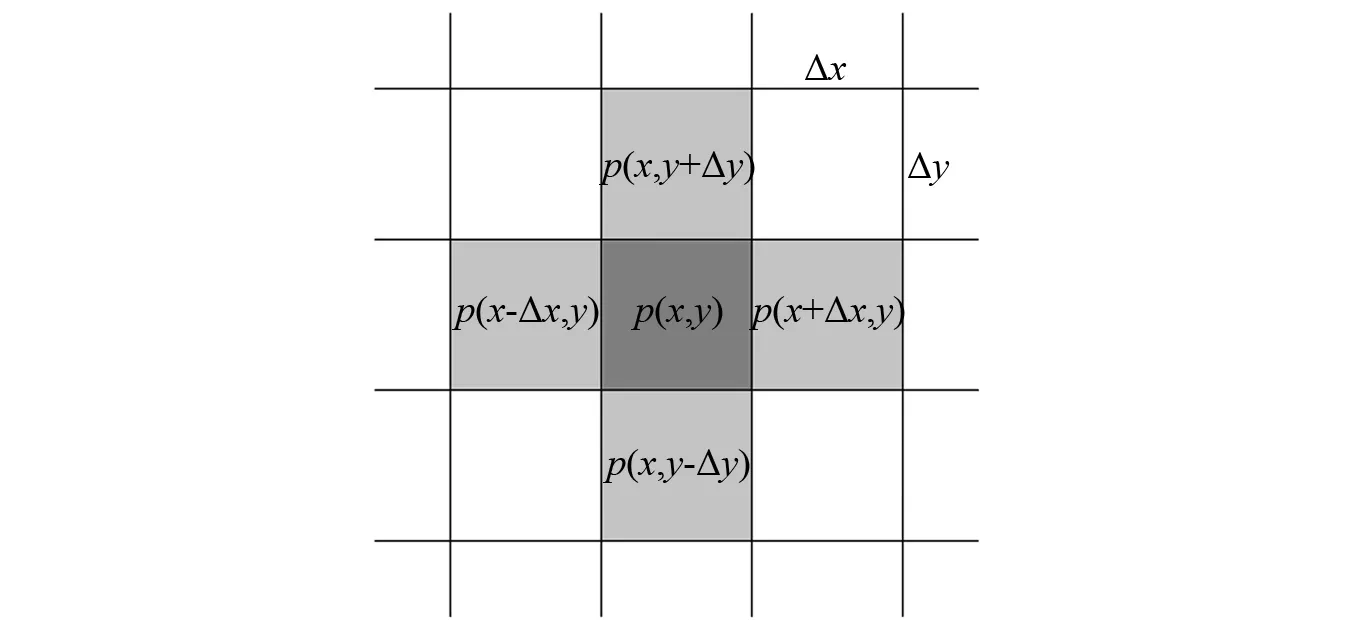
圖7 二維聲學CA模型鄰居Fig.7 Neighbors of 2D acoustic CA model

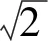
φ=(c·Δt/Δl)2=(c/ca)2=1/2

(13)

將式(13)代入式(12)，可得Von Neumann型二維聲學CA模型的局部演化規則

p(x,y,t+Δt)=0.5{p(x+Δx,y,t)+
p(x-Δx,y,t)+p(x,y+Δy,t)+p(x,y-Δy,t)}-p(x,y,t-Δt)

(14)

Komatsuzaki等的研究曾利用Von Neumann型CA求解點聲源自由空間的輻射聲場，聲場中過點源的某一切片結果，如圖8所示。由圖8可知：在聲源附近和離聲源較遠位置處，解析解和CA解相差不大，但是在離聲源一定距離的位置上，解析解與CA解相差很大，最大誤差在50%以上，這是由CA模型各向異性的更新規則所致。

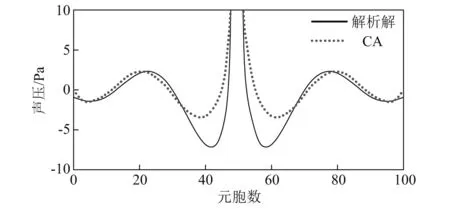
圖8 Komatsuzaki等的研究中點源輻射聲場聲壓分布Fig.8 Distribution of sound pressure in the radiated sound field of point source in Komatsuzaki et al research

3.2 脈動球源輻射聲場

為解決二維聲學CA模型中狀態變量更新的各向異性問題，在導出局部演化規則時可將直角坐標變換為球坐標，以脈動球源為例，坐標原點取在球心，其球坐標下的聲傳播二維聲波方程為

(15)

式中：r為空間任一點至球心的距離；p為r，t的聲壓函數；S為r處波陣面面積；c為聲速。令Y=pr，則式(15)變換為

(16)

可以發現，式(16)與一維聲波方程類似，那么應用CA方法求解脈動球源二維聲場聲壓時，可先建立Y函數的一維CA模型，在解出二維聲場中任意場點的Y值之后，只需將Y值比上該場點至球心的距離r即可得到二維聲場中任意場點的聲壓值p。

算例1假設在二維自由空間中存在一個脈動球源，以球心為中心，取10 m×10 m的矩形區域為計算空間，將計算空間以邊長為0.1 m的正方形網格劃分為100×100個像元，計算參數如表2所示。自由空間脈動球源聲場聲壓解析解表達式為

表2 計算參數Tab.2 Calculation parameters

(17)

式中：ρ為介質密度；k為波數；r0為球源半徑；u為球源振速幅值；θ按式(18)計算

θ=arctan(1/kr0)

(18)

將計算區域聲壓分布解析解與球坐標下的CA解對比，如圖9所示。二維自由空間計算區域內豎向和對角切片的聲壓分布，如圖10所示。

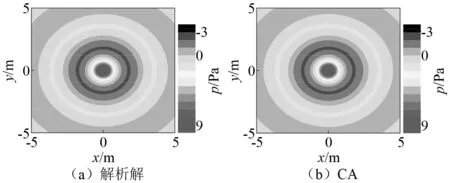
圖9 自由空間脈動球源輻射聲壓云圖Fig.9 Nephograms of sound pressure radiated by pulsating sphere source in free space

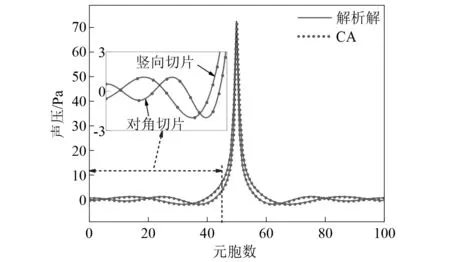
圖10 豎向與對角方向聲壓分布Fig.10 Distribution of sound pressure in vertical and diagonal directions

由圖9和圖10可知：CA結果顯示，二維脈動球源在自由空間內的聲輻射形狀為圓周，且聲壓隨距離r的增大而減小，近場聲壓衰減快，遠場聲壓衰減慢，這與球源輻射聲場性質一致；解析解與CA解吻合良好，表明本文所建立的二維CA模型能準確求解脈動球源自由空間聲輻射問題；采用球坐標聲波方程導出Y函數一維CA模型局部演化規則，進而求解二維聲場聲壓的方法，可避免二維CA模型中元胞狀態變量各向異性更新的問題。

算例2假設在二維半自由空間中存在一個脈動球源1，距離球源下方5 m處有一無限大剛性壁面，以球心為中心，取10 m×10 m的矩形區域為計算空間，將計算空間以邊長為0.1 m的正方形網格劃分為100×100個像元，如圖11所示。計算參數如表2所示。由鏡像原理可知，半自由空間脈動球源1聲場等效于自由空間脈動球源1及其沿剛壁鏡像球源2聲場的疊加，此時聲場聲壓解析解表達式為

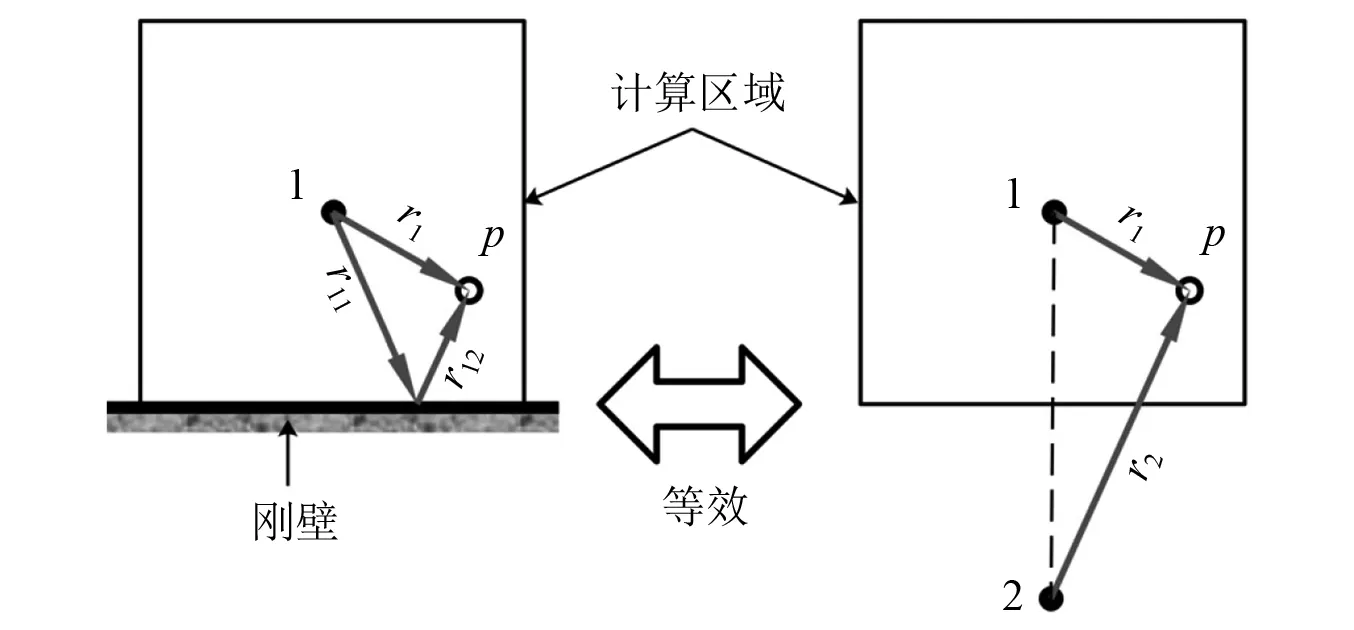
圖11 半自由空間脈動球源輻射聲場Fig.11 Sound field radiated by pulsating sphere source in half free space

(19)

其中，

(20)

將計算區域聲壓分布解析解與CA解對比，如圖12所示。二維半自由空間計算區域內橫向、豎向和對角切片的聲壓分布，如圖13所示。

圖12 半自由空間脈動球源輻射聲壓云圖Fig.12 Nephograms of sound pressure radiated by pulsating sphere source in half free space

由圖12與圖13可知：解析解與CA解吻合良好，表明本文所建立的二維CA模型能準確求解脈動球源半自由空間聲輻射問題；同時也說明了對于雙球源組合聲場，該模型依舊具有較高的計算精度和良好的適用性。

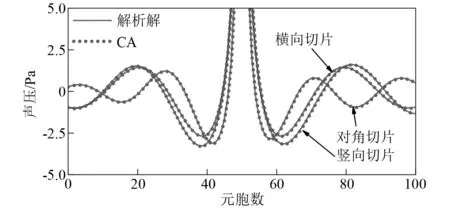
圖13 橫向、豎向與對角方向聲壓分布Fig.13 Distribution of sound pressure in transverse,vertical and diagonal directions

4 結 論

本文利用CA方法對聲管和脈動球源聲學問題進行建模，分析了一維平面波與二維球面波聲場規律，并將聲學CA模型計算結果與解析解進行對比，得到以下幾點結論：

(1)本文建立的聲學CA模型能準確模擬平面波與球面波場聲輻射規律，且結果與聲波方程的解吻合程度高。

(2)一維CA模型的局部演化規則可直接由聲波方程導出；而直接按聲波方程導出二維CA模型的局部演化規則會使元胞狀態變量更新存在各向異性的問題。

(3)采用球坐標聲波方程導出脈動球源Y函數一維CA模型的局部演化規則，進而求解二維聲場聲壓的方法，可避免二維CA模型中元胞狀態變量各向異性更新的問題。

(4)對于雙球源組合聲場，聲學CA模型依舊具有較高的計算精度和良好的適用性；那么對于多點源組合成的面聲源輻射聲場，利用CA方法分析其聲場性質是否可行，這將在下一步工作中繼續探討。