基于量子粒子群算法的主動懸架分數階控制策略
許 力,曹青松,張定軍
(江西科技學院 機械工程學院,南昌 330098)
主動懸架可以簡單看成由被動懸架與作動器組成的一種新型懸架,作動器可實時依據路面信息及車身振動情況按照控制規律對車身產生一個力的作用,來平衡路面的沖擊,提高車輛平順性與乘坐舒適性。所以,作動器控制策略影響著主動懸架性能,相關研究也受到國內外許多學者的廣泛關注,已經提出了以整數階微積分理論作為基礎的主動懸架滑模控制、自適應控制、模糊控制等諸多控制策略[1-3]。
近年來,由于分數階微積分的記憶特性,能更真實地描述具有黏彈、滯回等非線性物體的數學模型,越來越多地應用于磁流變液或油氣主動懸架的數學建模上[4-5]。孫會來等[6]采用Caputo分數階微積分對油氣懸架進行數學建模,通過試驗證明了分數階模型比整數階模型更為精確。此外,分數階微積分對被控對象參數的變化具有較強魯棒性等優點[7-8],許多學者將分數階微積分理論應用于主動懸架的控制器設計。Tar等[9]基于包含空氣彈簧、黏性阻尼彈簧和液壓非線性阻尼器的模型,引入分數階控制器以抑制路面帶來的振蕩。梁軍等[10]將其應用于半主動懸架的天棚控制中,對天棚阻尼系數進行優化,提高了平順性。高遠等[11]提出一種以分數階微分信號作為控制器輸入的分數階模糊控制方法。陳炎冬等[12]在主動懸架滑模控制中引入分數階趨近率,有效削弱了滑模控制中抖振問題。
在分數階控制器設計過程中,由于增加了積分階次或微分階次等參數,從而使控制器參數整定變得更加復雜。許多學者為簡化參數整定過程,將分數階微積分進行等效逼近[13]再采用各類數字算法對其參數進行優選。Dong等[14]基于電液懸架線性模型,設計了分數階PIλDμ控制器,采用克隆選擇算法對參數進行整定。吳光強等[15]采用Oustaloup濾波器算法對分數階天棚阻尼半主動懸架進行參數整定,與被動懸架、整數階主動懸架對比分析。陳炎冬等[16]采用遺傳算法對主動懸架分數階控制器參數進行優化,通過仿真表明,其對削弱車身共振效果明顯優于整數階PID控制器。游浩等[17]針對1/4車輛被動懸架,建立分數階數學模型,采用粒子群算(particle swarm optimization,PSO)法對彈簧剛度和阻尼系數進行優化,優化后乘車舒適性可明顯改善。張欣等[18]針對高低溫試驗箱分數階被控系統,設計一個分數階PIλDμ閉環控制器,利用量子粒子群算法(quantum particle swarm optimization,QPSO)對控制器參數進行整定,采用量子旋轉門對粒子位置進行更新,并與PSO整定方法比較,得出QPSO具有更強的尋優能力。
本文基于上述研究背景,建立基于分數階PIλDμ控制器的1/4懸架模型,采用QPSO算法對PIλDμ進行參數整定,建立集合車身垂向加速度、懸架動撓度和車輪動載荷的綜合評價函數,從時域和頻域分析被動懸架、整數階主動懸架和分數階主動懸架的控制性能。
1 分數階微積分與Outstaloup逼近法
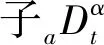
(1)
由式(1)可知,分數階微積分算子sα的幅頻特性曲線是以20αdB/dec為斜率的直線,相頻特性為恒定值α·(π/2)。整數階微積分中α只能為正整數或負整數,幅頻和相頻相對固定、不易調節,分數階微積分中α可以為任意實數,幅頻和相頻特性調節更為方便。
關于分數階微積分的數值計算,不同的定義式有不同的計算方法,通常計算結果受步長h影響較大。要更準確地計算其數值,h值越小越好,累加次數相應增多,計算量更大。將分數階微積分分成幾個頻率段,并在各頻率段內用不同階次的整數階微積分進行擬合近似,可得到較為準確的計算結果,且減小了累加次數。本文采用的是改進型Outstaloup逼近算法,在某一頻率段(ωb,ωh)內對分數階微積分算子sα可近似為整數階零極點型式的累乘。
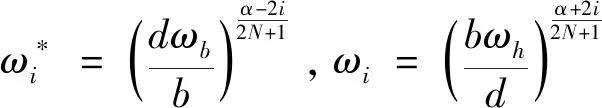
在頻率段(0.001 rad/s,1 000 rad/s)內,-0.5階微分算子伯德圖在濾波器階次分別為1,3,5時的曲線,如圖1所示。濾波器階次越高,逼近效果越好,但是增加了累乘次數,所以本文選取的濾波器階次N為3。
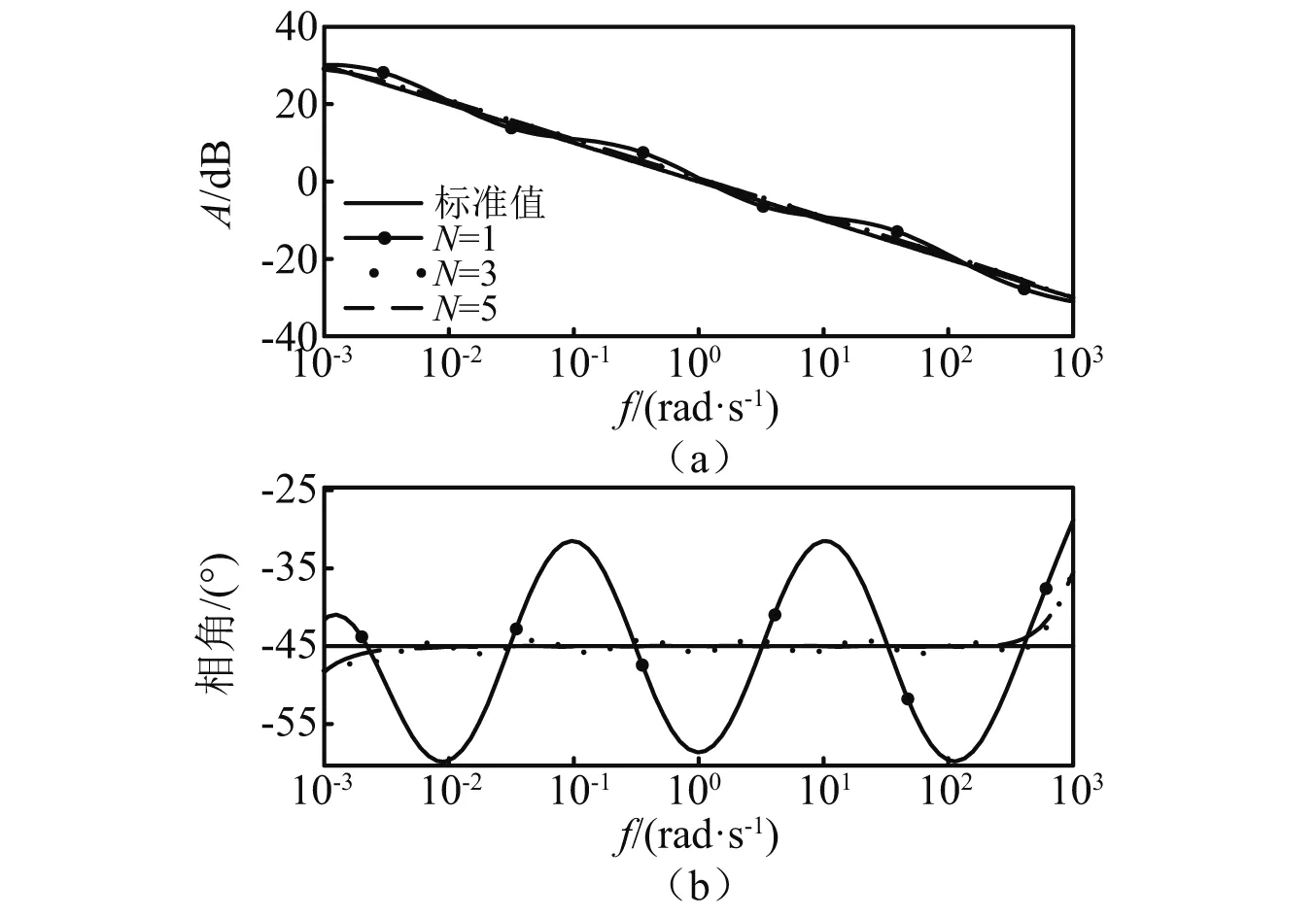
圖1 不同階次濾波器逼近效果Fig.1 Approximation effect of different order filters
2 基于分數階控制器的主動懸架模型
2.1 1/4車輛主動懸架模型
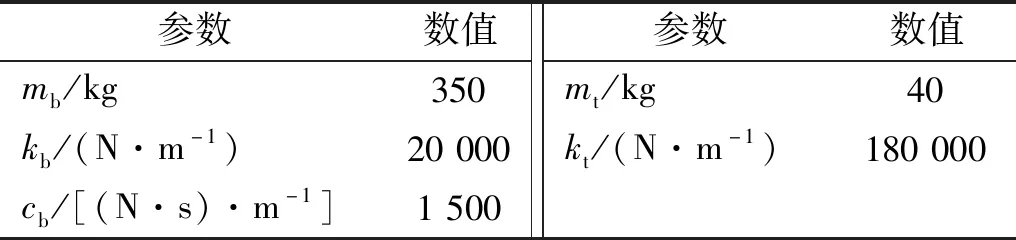
圖2所示為1/4懸架振動模型,忽略了輪胎阻尼,圖中:mb為車身質量,mt為輪胎質量,kb為車身懸架剛度,cb為懸架阻尼系數,xb,xt分別為車身和輪胎的垂向位移,x0為路面輸入,u為作動器輸出的力。那么,主動懸架系統的線性動力學微分方程為
(3)
2.2 基于分數階PIλDμ控制器的懸架模型
圖2中u是由車身加速度誤差信號經PIλDμ控制器得到,如式(4)所示
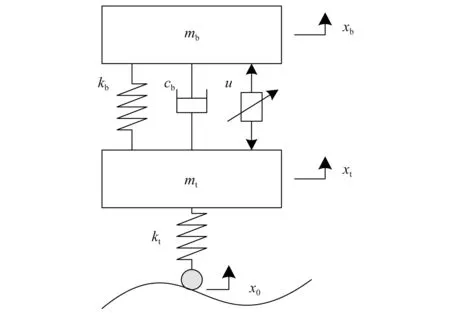
圖2 主動懸架系統模型Fig.2 Active suspension system model
U(s)=-F(s)s2Xb
(4)
對式(3)兩邊做拉普拉斯變換,可得車身位移和輪胎位移對路面激勵的傳遞函數,分別如下所示
(5)
(6)
式中:A(s)=s2[F(s)+mb]+B(s);B(s)=cbs+kb。
同時,分數階控制器PIλDμ是在整數階PID控制器的比例系數、積分系數、微分系數3個可調參數基礎上,再引入可調的積分階次參數λ和微分階次參數μ,其能靈活地調節控制器。分數階PIλDμ控制器的時域表達式為
(7)
其傳遞函數為
F(s)=kp+kis-λ+kdsμ
(8)
當F(s)=0時,為被動懸架;當F(s)=kp+kis-1+kds時,為含整數階PID控制器的主動懸架;當式(4)中的F(s)為式(8)時,則為含分數階PID控制器的主動懸架。因此,可設計如圖3所示含分數階PID控制器的主動懸架控制系統。

圖3 系統控制框圖Fig.3 System control block diagram
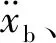
(9)
式中:g為重力加速度,取9.8 m/s2;fd_max為懸架動行程最大值,取0.1 m;l1,l2,l3為加權系數,定義域均為(0,1),三者之和為1,根據主動懸架不同性能的需要而設置加權系數大小。
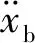
3 主動懸架分數階PIλDμ參數量子粒子群優化
3.1 量子粒子群優化算法(QPSO)
QPSO算法是一種具有全局搜索能力的智能算法,解決了PSO算法容易陷入局部最優解的問題。在粒子進化時,群體中的大部分粒子可能聚集在次優解附近,只有少部分粒子遠離次優解,為了避免粒子過早向次優解聚集而引起的早熟現象,本文引入群體平均最佳粒子作為粒子進化因素之一,這樣可使遠離次優解的粒子做全局搜索,找到最優解。
將[Kp,Ki,Kd,λ,μ]看成五維解空間中粒子,并找出使主動懸架的評價函數值最小的粒子,這些粒子具有量子特性,隨迭代次數的增加而進化。每次進化,粒子依據個體最佳粒子Pi(t)、群體最佳粒子G(t)、群體平均最佳粒子C(t)以及隨機函數組合成的進化規則而進行更新。C(t)可防止群體陷于早熟,隨機函數使得粒子能以不同的概率出現在解空間各個位置,降低了局部最優可能性。其進化規則如下式所示
Xi,j(t+1)=±α·|Cj(t)-Xi,j(t)|·ln[1/ui,j(t)]+
si,j(t)
(10)
其中,
si,j(t)=φi,j(t)·Pi,j(t)+[1-φi,j(t)]·Gj(t)
(11)
(12)
式中:t為第t次迭代;Xi,j為第i粒子第j維;α為收縮-擴張系數,令其由首次迭代時為1并線性衰減至迭代結束時為0.5;ui,j(t),φi,j(t)為第t次迭代第i粒子第j維的概率函數,且ui,j(t),φi,j(t)~U(0,1);Pi,j為第i粒子的個體最佳粒子的第j維;Gj為粒子群最佳粒子的第j維;Cj為粒子群平均最佳粒子的第j維;M為粒子群粒子個數。
3.2 主動懸架分數階控制器參數優化與確定
根據3.1節QPSO算法的思想,主動懸架分數階控制器參數具體整定流程圖如圖4所示。
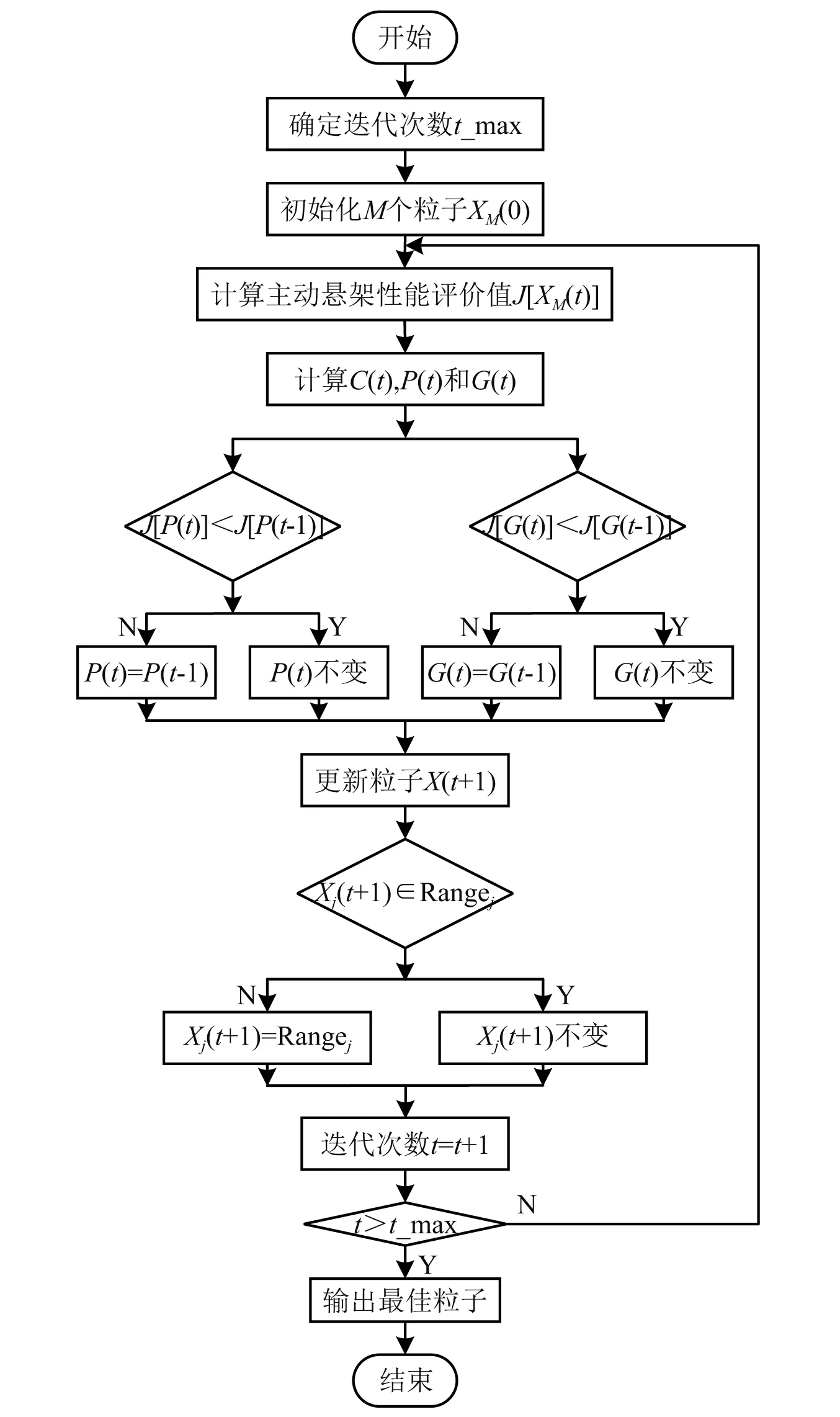
圖4 QPSO參數整定流程圖Fig.4 Flow chat of setting parameters by QPSO
步驟1初始化,設置迭代次數t_max及粒子初始值。將控制器參數[Kp,Ki,Kd,λ,μ]看成五維空間中粒子,在其取值區間內隨機生成M個粒子當作初始值,并且此M個粒子看成首次迭代中的個體最佳粒子Pi(0)。
步驟2將步驟1生成的各粒子代入式(5)、式(6),得到車身垂向加速度、懸架動撓度和車輪相對動載荷值,并將這3個值代入式(9)得到各粒子對應的綜合評價值J[Xi(0)]。找到M個粒子中評價值最小的那個粒子記為G(0)。同時,計算M個粒子的平均值C(0)。利用式(10)~式(12)獲得M個新粒子XM(1)。
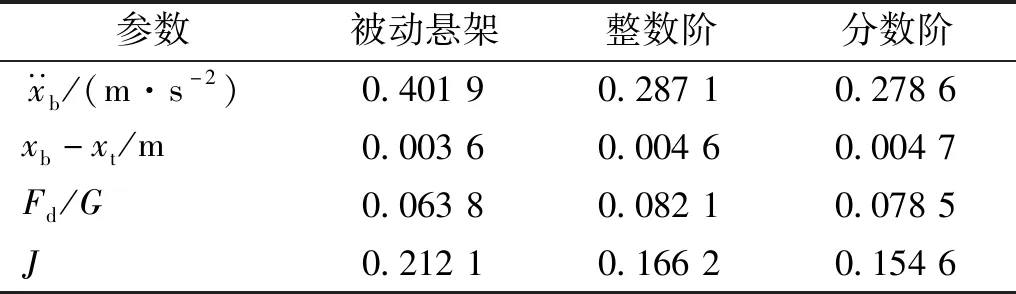
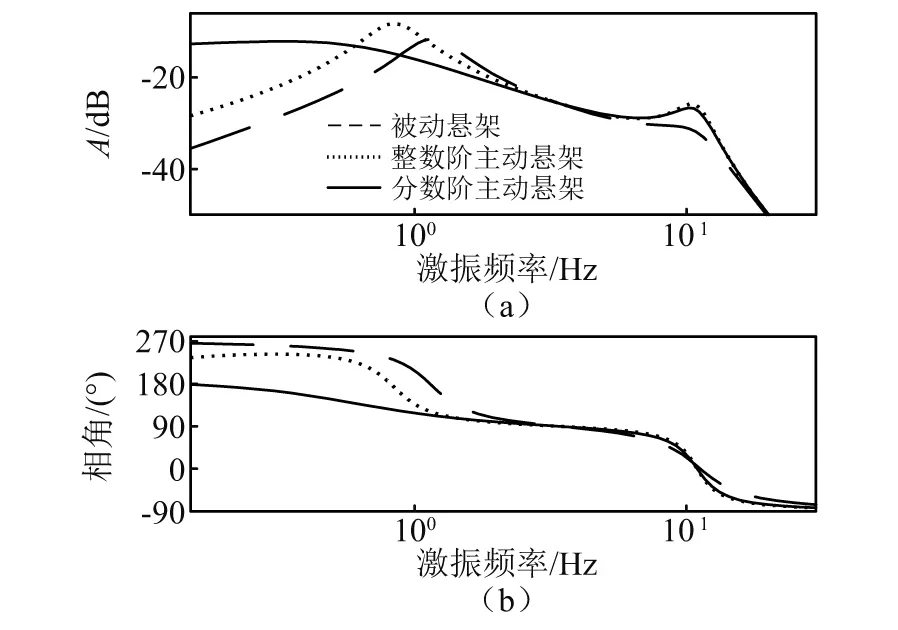
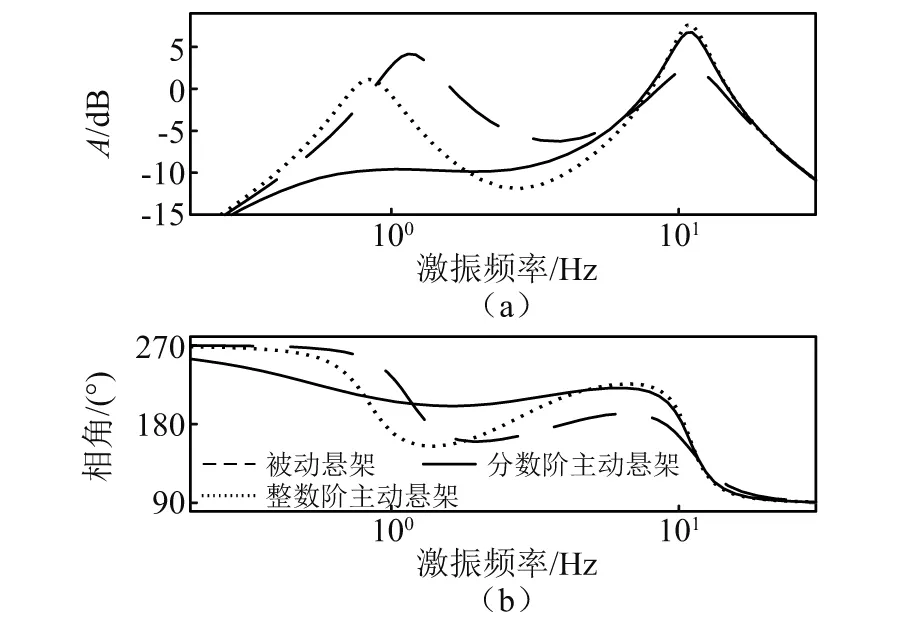
步驟3計算粒子更新后的綜合評價值,找出本次迭代最佳粒子G(t)(綜合評價值小者為佳),并判斷J[G(t)] 步驟4找出本次迭代每個個體最佳粒子Pi(t),判斷方法與步驟3一致,并計算出的平均最佳粒子C(t)。 步驟5根據式(10)~式(12)更新出下次迭代的所有粒子XM(t+1),并判斷新粒子各維是否超出邊界Range,若超出,則用邊界值代替那一維,否則,粒子值不變。回到步驟3。 步驟6迭代結束,輸出所有迭代過程所有粒子中使懸架綜合評價指標值最小的那個粒子。 懸架系統參數如表1所示。設定式(8)中加權系數為:l1=0.8,l2=0.1,l3=0.1。依據3.2節的算法,設定t_max=100,M=50,Kp∈(-1 000,1 000),λ∈(-1,0),μ∈(0,1),Ki,Kd∈(-5 000,5 000)。路面輸入為采用濾波白噪聲法生成的車速為30 km/h的B級路面隨機激勵信號,其時域曲線如圖5所示。 表1 懸架參數Tab.1 Suspension parameters 圖5 路面激勵Fig.5 Road excitation 圖6所示為兩種主動懸架參數整定過程,相比于QPSO整數階參數整定,對分數階參數進行整定時,J值更小并更容易收斂至最優值,全體粒子也更容易達到最佳位置。說明雖然分數階參數比整數解參數多了兩個,但利用QPSO對分數階參數整定時,效率更高。 圖6 參數整定過程Fig.6 Parameters setting process 求得整數階控制器參數為:[334.5,362.9,0],分數階控制器參數為:[54.39,3 750,69.59,-0.887 3,0.273 5]。 對被動懸架、整數階主動懸架和分數階主動懸架進行時域仿真分析,觀測車身垂向加速度、懸架動撓度及車輪相對動載荷的變化趨勢。表2為3個觀測參數的均方根值,圖7~圖9為觀測參數時域曲線,圖10為兩種主動懸架作動器輸出的作用力時域曲線。 表2 被測參數均方根值Tab.2 RMS of measured parameters 見表2所示,相比于被動懸架,整數階控制方式及分數階控制方式下的主動懸架綜合性能分別提升了21.64%和27.11%。車身垂向加速度降低明顯,其中整數階主動懸架下降了28.56%,分數階主動懸架降低了30.8%。結合圖7,分數階主動懸架的瞬時值相對最小,被動懸架的瞬時值相對最高。所以由QPSO確定參數的兩種主動懸架均可減小車身垂向加速度,提升車輛平順性,并且分數階主動懸架相對整數階主動懸架提升的更明顯。 圖7 車身垂向加速度時域曲線Fig.7 Vertical acceleration of vehicle body 在懸架動撓度方面,表2所示的被動懸架均方根值最小,而分數階主動懸架相對最大,但與整數階主動懸架相差不多。結合圖8可知:分數階懸架動撓度的最大值與整數階主動懸架相比有所下降,相比被動懸架其最大值幾乎相等,均在0.016 m附近。在車輪相對動載荷上,被動懸架也是表現最為良好的。結合表2和圖9可知:無論是均方根值還是瞬時值,分數階主動懸架均優于整數階主動懸架。總體來看:分數階主動懸架相比整數階主動懸架能夠進一步增強車輛的減振性能,提升了平順性。 圖8 懸架動撓度時域曲線Fig.8 Dynamic deflection of suspension 圖9 車輪相對動載荷時域曲線Fig.9 Wheel relative dynamic load 圖10為兩種主動懸架控制力的輸出曲線,整數階控制力均方根值為96.67 N,均方根值為108.1 N。分數階控制的作動器相比整數階控制在增加汽車平順性同時,加大了作動器的輸出。然而,相對于分數階控制的輸出,整數階作動器在相同時間內,正負變化相對頻繁。 圖10 作動器輸出Fig.10 Actuator output 根據式(5)、式(6)可求出車身垂向加速度、懸架動撓度和車輪-路面相對動位移對路面激勵導數的傳遞函數。其伯德圖如圖11、圖12、圖13所示。 圖對頻域特性Fig.11 Frequency-domain 圖12 xb-xt對頻域特性Fig.12 Frequency-domain characteristics of xb-xt versus 圖13 Fd/G對頻域特性Fig.13 Frequency-domain characteristics of Fd/G versus 由1/4車輛懸架的頻率特性可知:該模型有兩個共振點,分別處在1 Hz和10 Hz附近。由圖11可知:在1 Hz附近的共振點處,整數階和分數階控制的主動懸架相對被動懸架,其增益峰值分別減小了35%和69%,主動懸架對1 Hz處的共振有明顯抑制作用,但分數階的抑制效果更好,從而對車輛平順性有顯著改善。在3~10 Hz的頻率段,主動懸架的增益幅值明顯下降,并且兩種主動懸架對振動的抑制效果相差不大。在10 Hz及以上的頻率段內,兩種主動懸架對于平順性的改善效果不明顯。 由圖12可知:整數階主動懸架動撓度的增益在模型的兩個共振點處均保持較大值,分數階主動懸架在4 Hz以下的頻段內對懸架動撓度的增益最低,而在4 Hz以上頻段內,其增益相較于被動懸架惡化。 由圖13可知:在1 Hz左右的頻段內,分數階主動懸架車輪相對動載荷增益最低,在中間頻段整數階主動懸架增益最低,在10 Hz左右的頻段內,兩個主動懸架對車輪相對動載荷有明顯的惡化,這是因為評價指標的制約,相較而言,整數階主動懸架的惡化程度高于分數階主動懸架。綜合以上幅頻分析可知,分數階控制主動懸架對于低頻段減小共振效果明顯。 從圖11~圖13相位曲線來看:含分數階控制器的主動懸架系統低頻段相位變化更加平緩,高頻段相位變化與整數階主動懸架和被動懸架變化趨勢類似,分數階控制器更容易實現主動懸架控制系統的穩定性。 建立1/4主動懸架振動模型,采用量子粒子群優化算法對整數階控制器和分數階控制器進行參數整定,從時域、頻域兩方面對被動懸架、整數階主動懸架和分數階主動懸架進行對比研究。結果表明,主動懸架對車輛平順性有很大改善,相對于整數階主動懸架,分數階主動懸架在車身垂向加速度、懸架動撓度和車輪動載荷等指標方面均有一定程度的改善;相比被動懸架在高頻段有一定程度惡化,而低頻段分數階主動懸架性能改善明顯。因此,采用量子粒子群算法對含分數階控制器的主動懸架進行參數優化的方法可取,為主動懸架分數階控制器設計奠定基礎。4 仿真分析
4.1 仿真參數
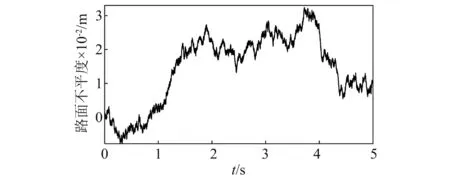
4.2 控制器參數整定過程
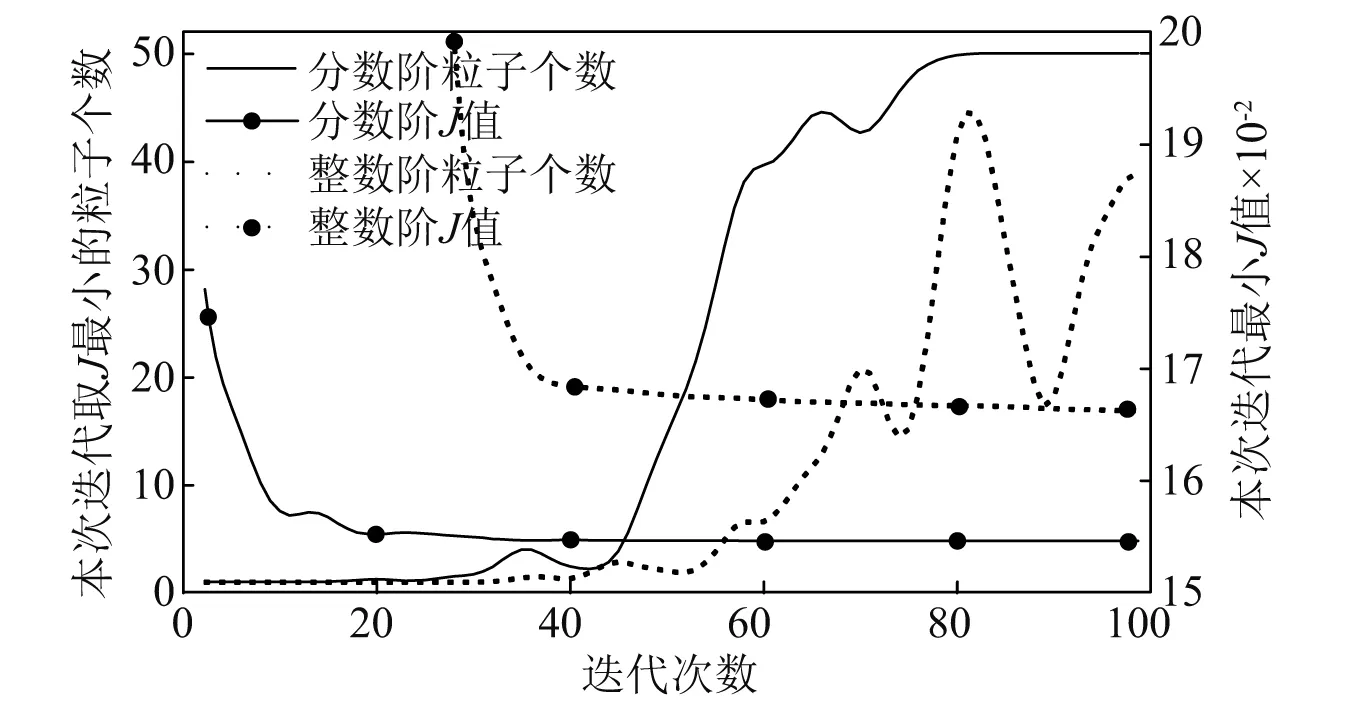
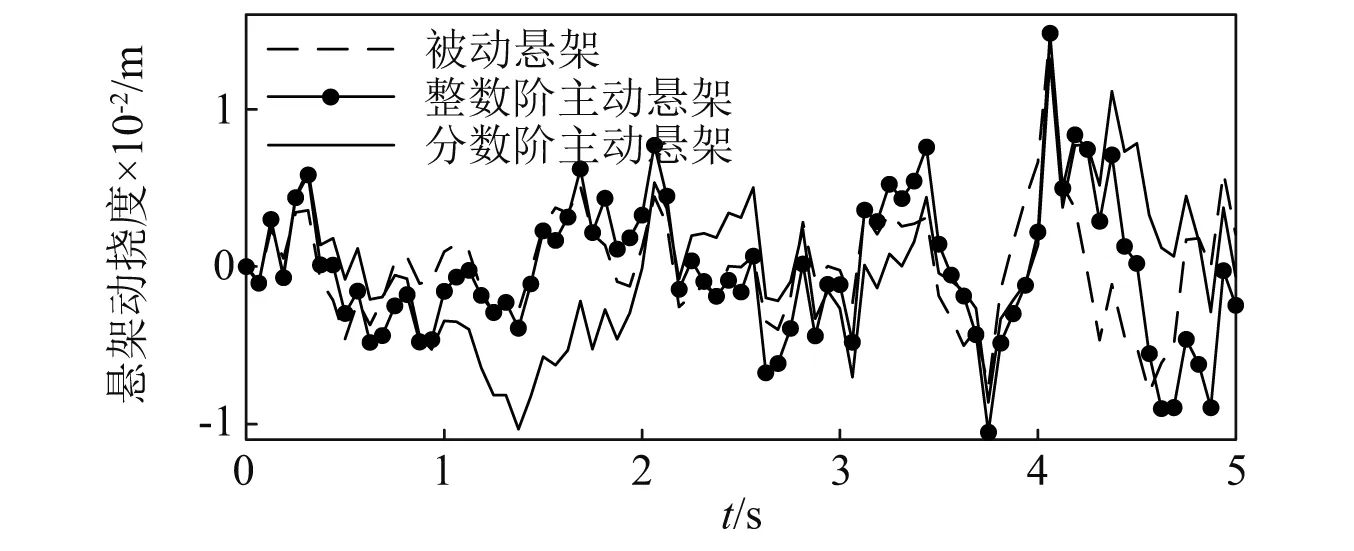
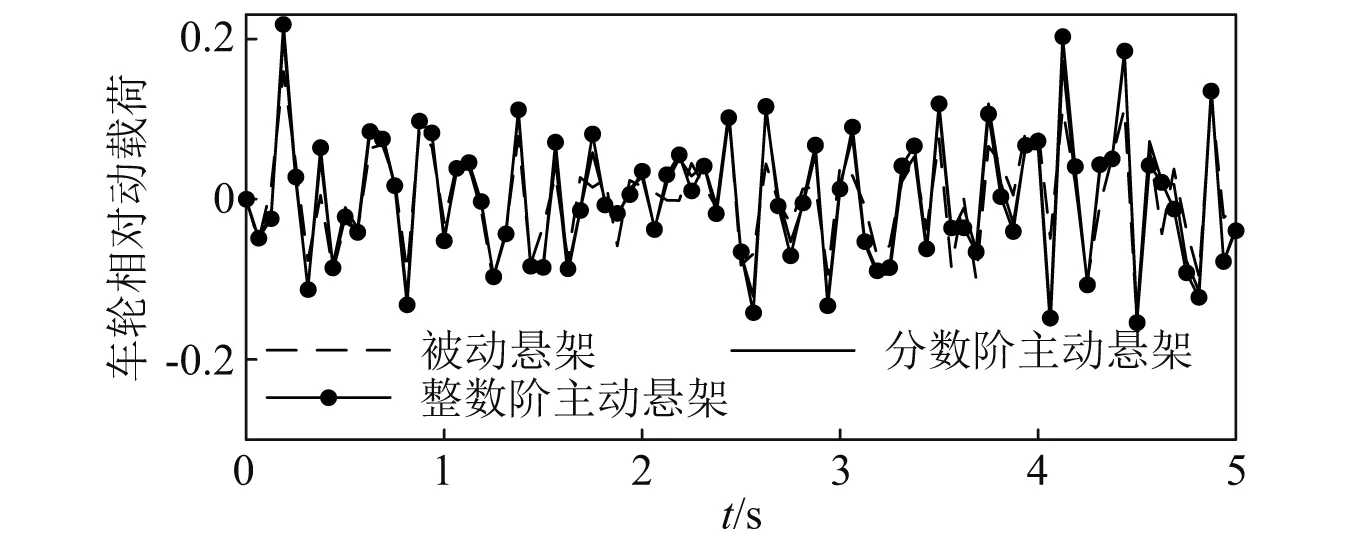
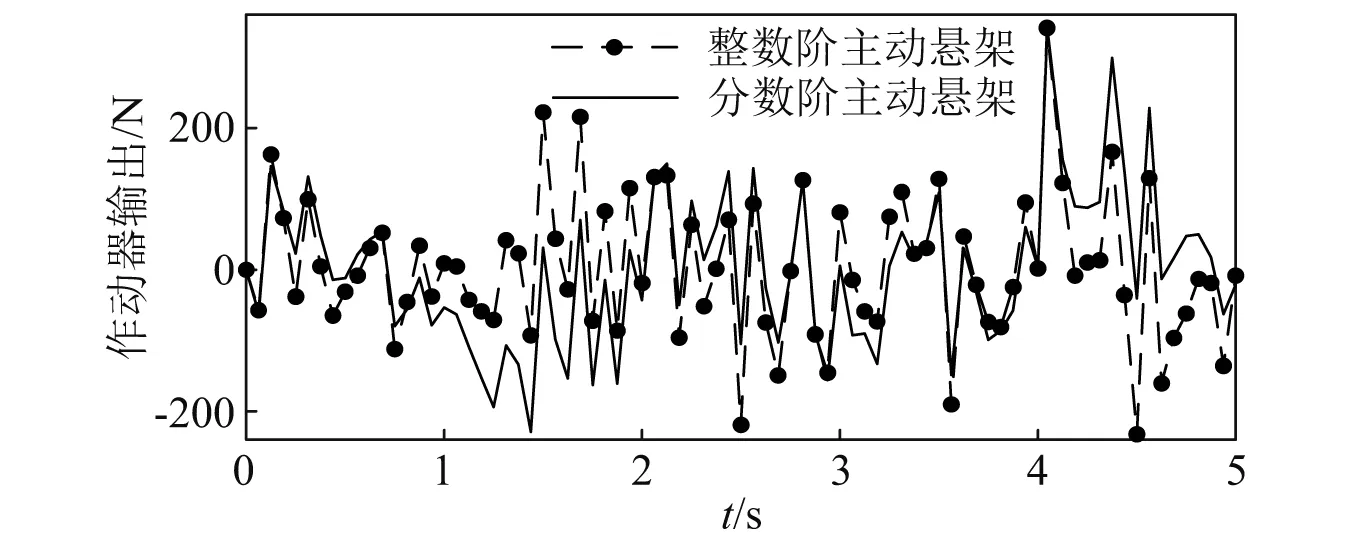
4.3 時域分析
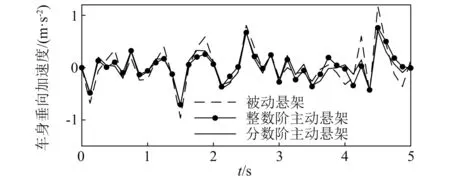
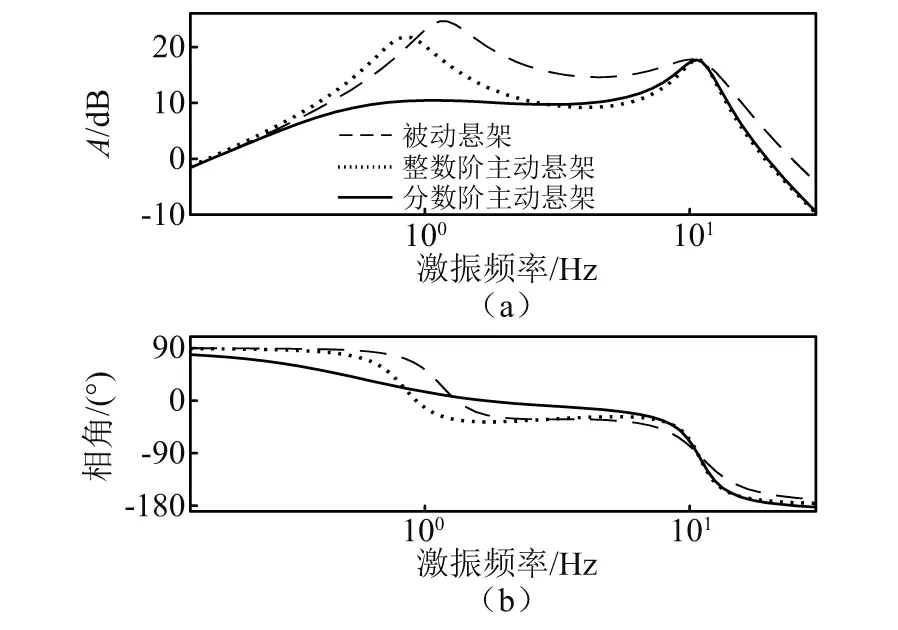
4.4 頻域特性分析
5 結 論

