基于經(jīng)驗小波變換的振動信號特征量提取
王 茜,田慕琴,宋建成,賀 穎,馮君玲,吝伶艷
(1.太原理工大學(xué) 礦用智能電器技術(shù)國家地方聯(lián)合工程實驗室,太原 030024;2.太原理工大學(xué) 煤礦電氣設(shè)備與智能控制山西省重點實驗室,太原 030024)
巖巷掘進機由于其有截割能力強等優(yōu)點成為我國煤巖巷道開采的主要設(shè)備[1]。但是由于掘進機工作環(huán)境惡劣,司機視野受限,傳統(tǒng)掘進機智能化水平偏低,司機無法根據(jù)掘進機狀態(tài)及時準(zhǔn)確地調(diào)整截割頭各項參數(shù),導(dǎo)致掘進機截齒受損,功率超限,壽命降低,因此提高掘進機智能化水平變得尤為重要[2]。截割頭動載荷識別是實現(xiàn)掘進機智能化的必要前提,而載荷的變化勢必會引起截割頭振動信號的變換,因此,通過對振動信號的變化分析可以完成掘進機動載荷的識別[3]。
特征提取是掘進機截割頭振動信號分析的重要一步,可以對掘進機所切割巖壁的硬度進行明顯劃分[4]。近年來,常用的振動信號提取方法主要以小波包分解為基礎(chǔ)進行變換。然而這些方法雖在一定程度上實現(xiàn)了掘進機振動信號去噪與特征量提取,并取得了較好的效果,但很大程度是依賴于最優(yōu)小波基函數(shù)以及信號分解層數(shù)的選擇[5],且當(dāng)信號幅值發(fā)生劇烈變化時,具有很大的局限性[6]。
經(jīng)驗小波變換(empirical wavelet transform,EWT)是由Gilles基于小波變換和窄帶信號分析理論提出來的,通過建立自適應(yīng)小波濾波器組來提取信號幅度和頻率調(diào)制分量[7]。近年來,通過國內(nèi)外學(xué)者的不斷研究,該方法以其計算方便等優(yōu)點被廣泛應(yīng)用于各個領(lǐng)域。
在實際工作中,掘進機截割頭切割巖壁時,巖壁硬度并不是一成不變的。不同巖壁硬度下掘進機的振動信號差異較大,所以需要對不同硬度下的振動信號進行分析并提取其特征量。針對以往掘進機截割頭振動信號分析方法的不足,本文提出了一種基于EWT和相關(guān)性閾值去噪相結(jié)合的信號特征提取方法。首先對不同巖壁硬度下的振動信號進行EWT分解,對各個分量進行相關(guān)性閾值去噪處理,此后計算各分量與原始信號之間的相關(guān)系數(shù),選擇相關(guān)性較高的分量構(gòu)成振動信號的特征矢量。
1 經(jīng)驗小波變換
1.1 經(jīng)驗小波變換原理
經(jīng)驗小波變換是一種經(jīng)驗?zāi)B(tài)分解原理與小波框架理論相結(jié)合的分析方法[8-11]。他通過小波框架理論構(gòu)造濾波器組,自適應(yīng)地將信號分解一系列頻率由高到低排列的AM-FM分量,從而提取特征量。經(jīng)驗小波變換原理如下。
步驟1對信號f(t)進行傅里葉變換得到其對應(yīng)的頻譜f(w)。
步驟2根據(jù)信號的頻譜圖,查找f(w)的局部極大值點并依次降序排列。根據(jù)極大值點對信號的頻域進行分段,取相鄰兩個極大值點間的中間數(shù)值作為頻域分界點wn(n=1,2,…)。
步驟3根據(jù)步驟2中的頻率分段構(gòu)造經(jīng)驗小波的小波函數(shù)ψn(w)和尺度函數(shù)φn(w),其表達式為
(1)
(2)
其中部分參數(shù)的計算方法為
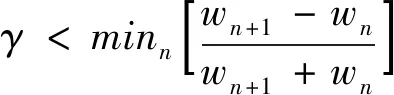
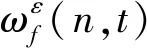
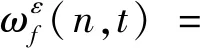
(3)
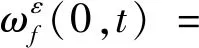
(4)
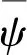
對信號進行重構(gòu),結(jié)果為
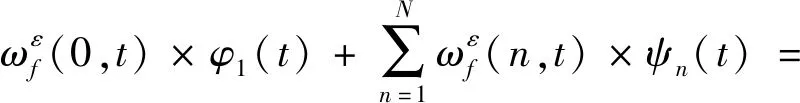
(5)
最終得到原始信號的經(jīng)驗小波函數(shù)為
(6)
(7)
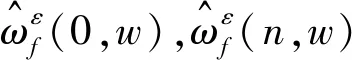
1.2 改進的經(jīng)驗小波變換
構(gòu)建采樣頻率為2 000 Hz,數(shù)據(jù)長度為1 024的仿真信號,其表達式為
y(t)=sin(100πt)+sin(60πt)+cos(40πt)
(8)
對該信號進行傅里葉分解得到頻譜圖,并根據(jù)極大值點進行頻帶劃分,如圖1所示。

圖1 仿真信號頻帶劃分Fig.1 Simulation signal band division
在仿真信號內(nèi)加入高斯白噪聲,再次進行傅里葉頻帶劃分,如圖2所示。
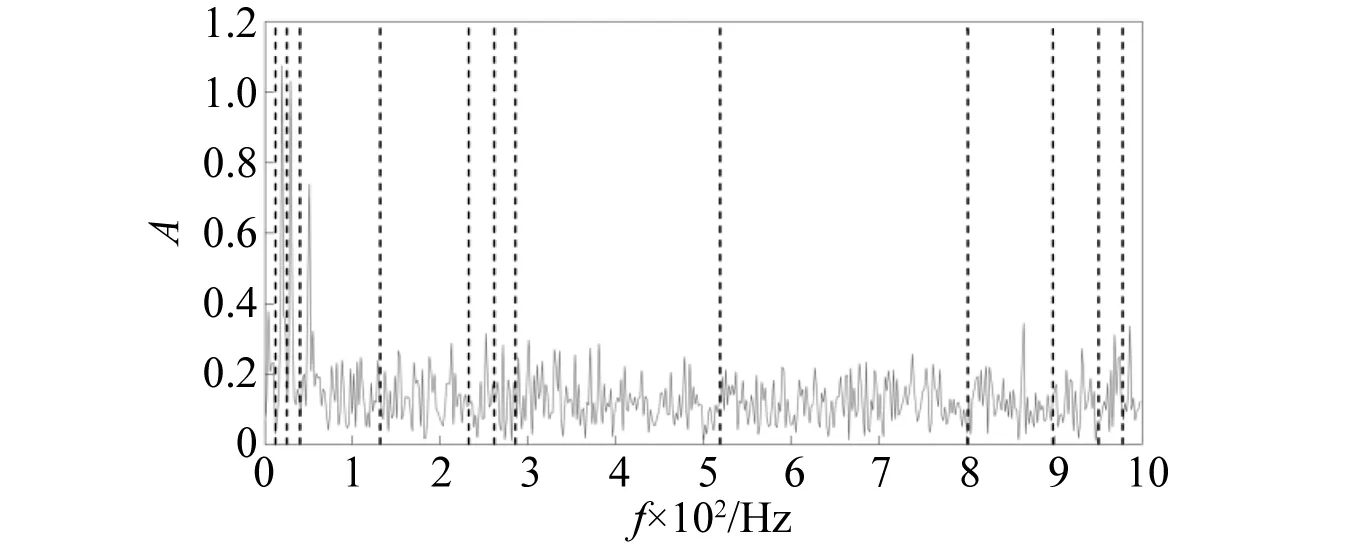
圖2 加噪后信號頻帶劃分Fig.2 Signal frequency band division after noise addition
由圖可知:噪聲的局部極大值點會極大的影響信號頻帶劃分的準(zhǔn)確性,降低經(jīng)驗小波變換信號處理的有效性,因此,本文將經(jīng)驗小波變換和相關(guān)性閾值去噪方法向結(jié)合,減少信號中噪聲的影響。
2 基于EWT的信號特征量提取
經(jīng)驗小波變換具有良好的自適應(yīng)性,而相關(guān)性閾值去噪法則具有很強的去噪能力,將兩種算法進行融合使用,首先對原始信號進行EWT,將原始信號信息分解到不同的頻帶內(nèi),對不同頻帶內(nèi)的分量進行去噪處理,提取與原始信號相關(guān)項較大的分量,然后分別利用奇異值分解對頻帶內(nèi)的信號進行去噪處理。具體操作方法如下。
步驟1利用相關(guān)性閾值去噪法對EWT分量進行去噪處理。
步驟2計算去噪后EWT各個分量與原始振動信號之間的相關(guān)系數(shù)rj(j=1,2,3,…,N)
式中:f為原始信號;ej為經(jīng)驗小波分量;σf和σej則為原始信號和各分量的標(biāo)準(zhǔn)差;n為各個分量的元素個數(shù)。
設(shè)置合理的閾值選取與原始信號相關(guān)性較大的經(jīng)驗小波分量,既可以去除包含特征信息較少的分量還可以達到降維的目的。通過查閱大量相關(guān)文獻,在本篇論文中,選取各相關(guān)系數(shù)的標(biāo)準(zhǔn)偏差作為閾值[12-13]。
步驟3計算步驟1中所選取的EWT分量的能量值
(10)
步驟4根據(jù)分量所得到的能量構(gòu)建原始信號的特征矢量,來表示掘進機截割頭所包含的信息。
V=[v1v2…vp]
(11)

步驟5將改進經(jīng)驗小波變換特征量提取的結(jié)果與奇異值分解特征量提取進行比較。
3 奇異值分解
奇異值分解(singular value decomposition,SVD)是一種非線性濾波方式[14-16],其基本步驟為:①對原始信號進行小波分解并構(gòu)造時頻矩陣;②對重構(gòu)矩陣進行奇異值分解;③信號還原。
任意一個秩為r的m×n維矩陣A都可以分解為m×m,n×n的兩個正交矩陣U和V,可表示為
Am×n=UΣV
(12)
式中,Σ=diag(σ1,σ2,…,σr,0,…,0)為對角矩陣,是矩陣A的奇異值,且滿足條件σ1≥σ2≥…≥σr>0。每一個奇異值均代表著原始信號的一個特征[17]。其中,較大的奇異值中包含了原始信號的主要特征,噪聲信號以及一些次要特征則被包含在較小的奇異值內(nèi)。
4 掘進機振動信號特征量提取
4.1 改進經(jīng)驗小波變換特征量提取
利用已經(jīng)搭建好的掘進機虛擬樣機模型,在ADAMS軟件中進行仿真,得到掘進機截割頭的振動信號,以巖壁硬度為6時z方向上的振動信號為例進行分析,在該信號內(nèi)添加信噪比為5的高斯白噪聲得到信號時域圖,如圖3所示。
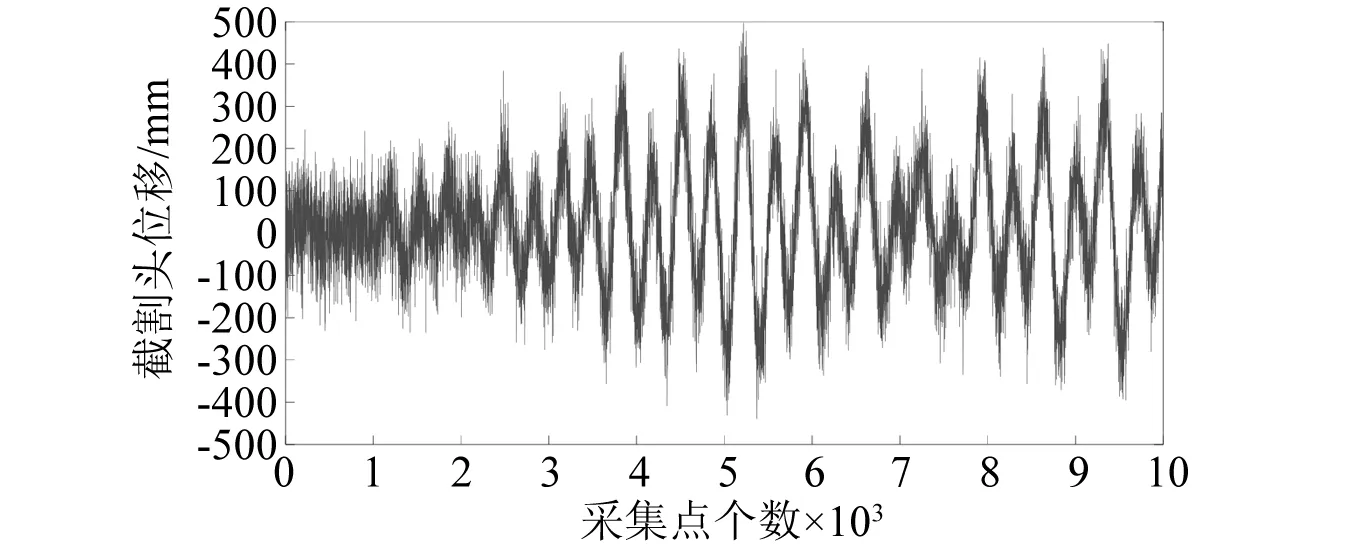
圖3 掘進機振動信號變換圖Fig.3 Vibration signal transformation diagram of roadheader
對原始信號進行傅里葉分析,得到振動信號的頻譜圖,如圖4所示。
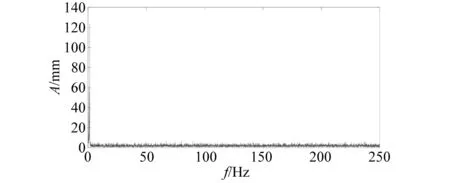
圖4 振動信號頻譜圖Fig.4 Spectrum of vibration signal
根據(jù)經(jīng)驗小波變換中提到的頻帶劃分原則,利用頻譜圖對鉆進工況下巖壁硬度分別為6,7,8時的截割頭振動信號信號進行頻帶劃分,得到分解后的EWT分量信號,如圖5所示。
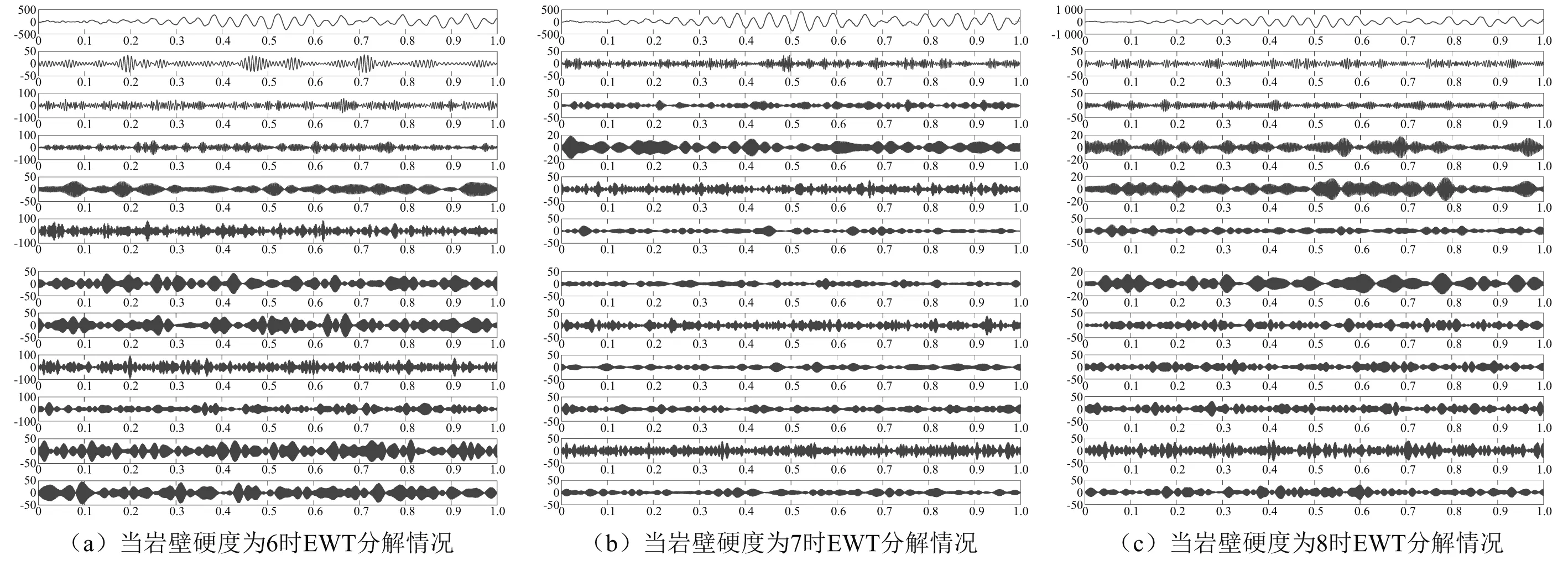
圖5 振動信號EWT分量時域圖(選取前幾個分量為例)Fig.5 Time domain diagram of the EWT component of the vibration signal (take the first few components as an example)
由圖5我們可以對不同巖壁硬度下的振動信號分量進行對比,可以發(fā)現(xiàn):不論在頻率還是幅值上均有顯著不同。這是由于掘進機在切割不同硬度巖壁時,會受到來自巖壁的反向阻力,且?guī)r壁硬度越大,所受到的阻力越大,并隨著掘進機切割深度發(fā)生規(guī)律性變換,最終導(dǎo)致掘進機截割頭的振動信號隨之發(fā)生相應(yīng)變化。
對各分量于初始信號的相關(guān)系數(shù)進行求解,其結(jié)果如圖6(a)所示。此后,利用相關(guān)性閾值去噪法對上述分量進行去噪處理,對去噪后的信號進行編號,計算各個分量與原始信號間的相關(guān)系數(shù),得到相關(guān)性的計算結(jié)果,如圖6(b)所示。
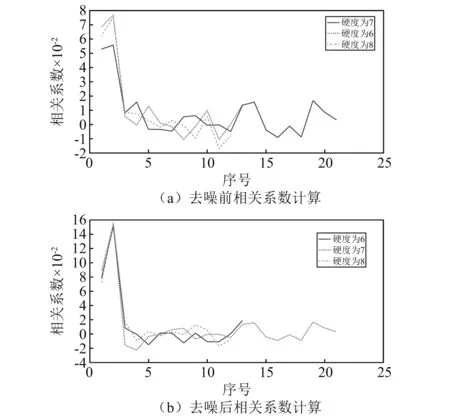
圖6 EWT分量相關(guān)系數(shù)計算Fig.6 EWT component correlation coefficient calculation
由圖6可以看出:去噪前后振動信號分量與原始信號的相關(guān)性都是先增大后急劇減小,最終逐漸在某個數(shù)值附近上下波動,其中,信號的第二個分量與原始信號的相關(guān)性最大。這是由于振動信號中始終存在一定的噪聲影響,并不能將其完全的剔除。但是,去噪后相關(guān)系數(shù)的值遠大于去噪之前,相關(guān)系數(shù)過小,信號受噪聲影響過大,在進行模式識別時不具有代表性,因此,要對信號進行消噪處理。此外,對比相同硬度下不同分量的相關(guān)系數(shù),我們可以看到,相關(guān)系數(shù)的值越大,說明該分量中所包含的掘進機截割頭的振動信號特性越多;而相關(guān)系數(shù)越小,說明該分量受噪聲影響越大,所包含的振動信號特性也相對較少。
本文以各分量與振動信號之間相關(guān)系數(shù)計算所得到的標(biāo)準(zhǔn)偏差作為閾值對振動信號分量進行刪選,不同煤巖硬度下均可以選取前兩位與原始信號相關(guān)性較大的作為特征矢量。
通過計算有效分量的能量作為掘進機截割頭振動信號的特征量,即可得到掘進機截割頭振動信號的特征量,如表1所示。

表1 不同巖壁硬度下z方向信號特征量Tab.1 Characteristics of z-direction signal under different rock wall hardness
用同樣的方法處理掘進機截割頭x,y方向上的振動信號,可以得到這兩個方向上的振動信號特征量,分別如表2和表3所示。

表2 不同巖壁硬度下x方向信號特征量Tab.2 Characteristics of x-direction signal under different rock wall hardness

表3 不同巖壁硬度下y方向信號特征量Tab.3 Characteristics of y-direction signal under different rock wall hardness
由表1~表3可以看出:在相同工況下,3個方向上振動信號的特征能量值基本上隨著切割巖壁硬度的增大而增大,且第一個分量能量特征值的增幅最為明顯,也就是說,第一個分量的能量特征值對掘進機切割巖壁的硬度變化最為敏感。在實際生活中,掘進機切割巖壁硬度越大,其振動信號變化越大,可見,振動信號的特征能量值在某種程度上確實可以反映信號的變化。
在同一巖壁硬度下的,掘進機截割頭x,y方向上的第一特征能量值要大于z方向上的特征能量值,但是x,y方向上的第二特征能量值在巖壁硬度發(fā)生變化時基本上保持不變,說明當(dāng)掘進機切割巖壁硬度發(fā)生變換時,z方向上的特征能量值對該變化反應(yīng)最為敏感。
4.2 對比分析
利用奇異值分解方法對掘進機截割頭z方向上的振動信號進行特征量提取,一般情況下,振動信號常用分解層數(shù)為6,7,8,比較不同分解層數(shù)以及不同小波基函數(shù)下振動信號所對應(yīng)的準(zhǔn)則值,得到結(jié)果如圖7所示。
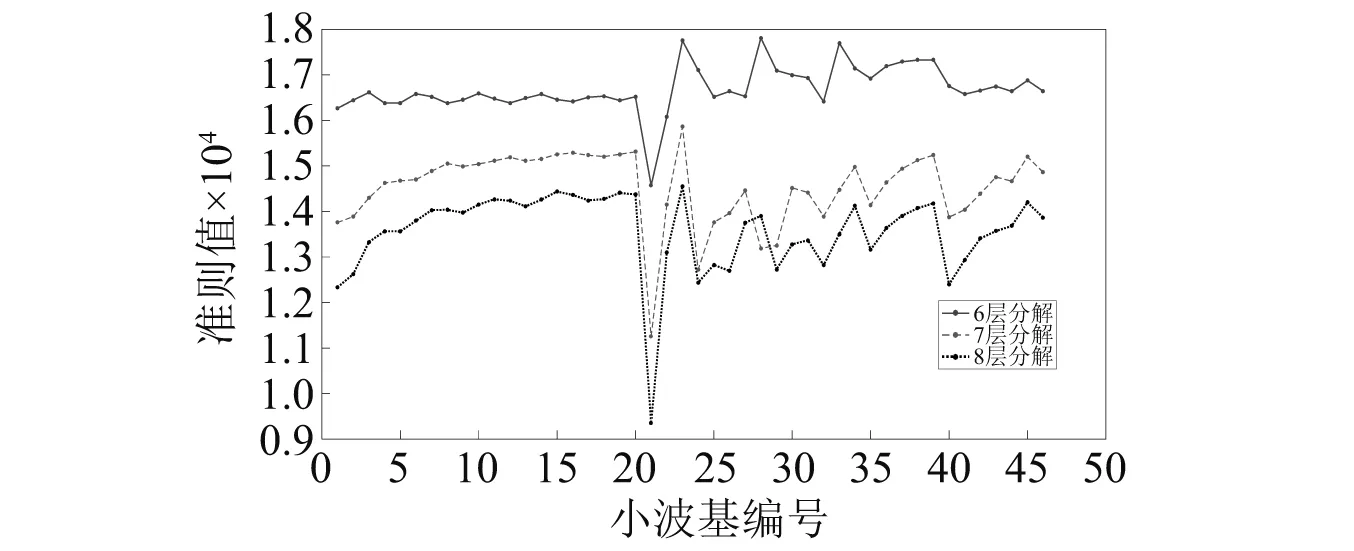
圖7 不同情況下振動信號準(zhǔn)則值Fig.7 Criterion values of vibration signals in different cases
由圖7可知:在同一小波基函數(shù)下,當(dāng)分解層數(shù)為6時提取的特征量準(zhǔn)則值普遍較大。當(dāng)分解層數(shù)為6,小波基函數(shù)為bior3.3時準(zhǔn)則值最大,提取的特征量向量最好,因此我們選取6和bior3.3為最優(yōu)分解層數(shù)和最優(yōu)小波基函數(shù)。在該條件下,對振動信號進行特征量提取,得到不同煤巖硬度下z方向上的特征量,如圖8所示。
由圖8可以看出:雖然利用奇異值分解法對振動信號進行處理的時候也可以對巖壁的硬度進行一個較為簡單的區(qū)分,但相對于改進的經(jīng)驗小波處理方法來講,奇異值分解方法處理后的特征量在巖壁硬度發(fā)生變換后,硬度較大時的特征量會與較低硬度的特征量存在重疊現(xiàn)象,并不能很好的對掘進機切割巖壁的硬度進行準(zhǔn)確的識別。
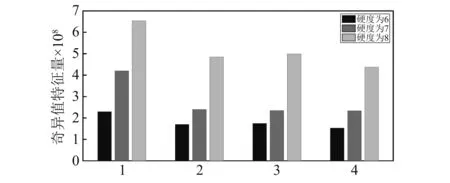
圖8 振動信號特征奇異值Fig.8 Singular value of vibration signal characteristics
5 結(jié) 論
(1)針對實際情況中掘進機截割頭振動信號特征量無法準(zhǔn)確提取的問題,提出了基于改進經(jīng)驗小波變換的特征量提取方法,為實現(xiàn)掘進機的動載荷識別提供了方法基礎(chǔ)。
(2)將經(jīng)驗小波變換與相關(guān)性閾值去噪法相結(jié)合,充分利用經(jīng)驗小波變換的自適應(yīng)性以及相關(guān)性閾值去噪的去噪能力,實現(xiàn)了在噪聲影響下振動信號特征量較為準(zhǔn)確的提取,為實現(xiàn)掘進機的智能化切割巖壁提供了技術(shù)基礎(chǔ)。
(3)對截割頭的振動信號進行處理得到其在不同巖壁硬度下的能量特征值,并將其與奇異值分解方法進行對比,證明前者所得到的特征量對巖壁硬度具有更好的識別性。

