汽輪機用3.5NiCrMoV鋼和20Cr13鋼的非對稱應變疲勞行為與壽命預測

吳海利

(上海電氣電站設備有限公司，上海 200240)

0 引 言

在汽輪機組啟動、調峰、停機等不同運行階段，其機組部件承受非對稱循環載荷。由于在高應力范圍內材料已進入塑性變形狀態，應力不再是最有意義的量[1]，因此研究其應變控制的疲勞行為顯得尤為重要。許多學者開展了低周疲勞壽命可靠性理論研究，提出了很多壽命預測公式和壽命可靠性模型。工程上應用較多的對稱疲勞壽命模型是MANSON[2]和COFFIN[3]提出的Manson-Coffin方程。在非對稱疲勞壽命預測方面：MORROW[4]提出在Manson-Coffin方程的基礎上進行平均應力修正；SMITH等[5]綜合考慮拉力分量作用下單軸應力和應變的影響提出了在Manson-Coffin方程引入最大應力和應變幅乘積作為損傷因子的SWT方程；ELLYIN等[6]考慮平均應力效應的影響提出了總循環應變能密度理論。

目前，學者們已經對汽輪機材料開展了很多低周疲勞試驗，并積累了大量對稱應變疲勞的基礎試驗數據。近年來在非對稱應變疲勞行為方面也開展了相應研究，例如：張孝忠等[7]對汽輪機長葉片材料開展了應變比R為0的非對稱低周疲勞試驗，建立了一種考慮平均應力松弛的葉根低周疲勞壽命預測方法；吳德龍[8]對汽輪機轉子材料高鉻鋼進行了600 ℃對稱和非對稱應變疲勞試驗，建立了與應變幅相關的循環軟化和平均應力松弛行為預測模型；還有一些學者對比了不同應變比下其他工程材料的非對稱疲勞循環曲線和循環壽命[9-11]。非對稱疲勞行為相對復雜，且壽命預測模型的適用性研究也較少。為充分理解非對稱應變疲勞力學響應特征，選用典型汽輪機用貝氏體基體轉子鋼3.5NiCrMoV和馬氏體基體葉片鋼20Cr13進行對稱和非對稱應變控制疲勞試驗，對其對稱和非對稱應變疲勞試驗數據進行對比分析，采用基于對稱應變疲勞參數的壽命模型對非對稱疲勞壽命進行估算，討論模型的適用性。

1 試樣制備與試驗方法

試驗材料包括典型汽輪機轉子用3.5NiCrMoV鋼和葉片用20Cr13鋼，2種試驗鋼的顯微組織如圖1所示，其中：3.5NiCrMoV鋼的基體組織為貝氏體，屈服強度為650 MPa，抗拉強度為780 MPa，彈性模量為230 GPa；20Cr13鋼的基體組織為馬氏體，屈服強度為674 MPa，抗拉強度為818 MPa，彈性模量為219 GPa。

圖1 3.5NiCrMoV鋼和20Cr13鋼的顯微組織Fig.1 Microstructures of 3.5NiCrMoV steel (a) and 20Cr13 steel (b)

按照GB/T 15248—2008，采用MTS810型電液伺服疲勞試驗機進行對稱和非對稱應變控制疲勞試驗。疲勞試樣為等截面圓柱試樣，直徑為8 mm。控制方式為軸向應變控制，試驗波形為三角波，應變速率為4×10-3s-1，試驗溫度為(23±2) ℃。對稱循環下的應變比Rε為-1，3.5NiCrMoV鋼和20Cr13鋼在非對稱循環下的應變比Rε分別為0，0.05，應變幅Δεt/2均為0.002～0.015。

2 試驗結果與討論

2.1 對稱與非對稱疲勞試驗數據的對比

由圖2可知：在應變幅為0.006，0.008下，3.5NiCrMoV鋼在Rε為-1時的對稱疲勞壽命Nf與Rε為0時的非對稱疲勞壽命相近，在其余應變幅下Rε為0時的非對稱疲勞壽命均低于Rε為-1時的對稱疲勞壽命；20Cr13鋼在Rε為0.05時的非對稱疲勞壽命均高于Rε為-1時的對稱疲勞壽命。

圖2 3.5NiCrMoV鋼和20Cr13鋼的應變幅-壽命曲線Fig.2 Strain amplitude-life curves of 3.5NiCrMoV steel (a) and 20Cr13 steel (b)

由圖3可知：在相同應變幅下，3.5NiCrMoV鋼在Rε為0時的應力幅σa遠低于Rε為-1時的應力幅，相差近200 MPa；而20Cr13鋼在Rε為0.05時的應力幅與Rε為-1時的相近。

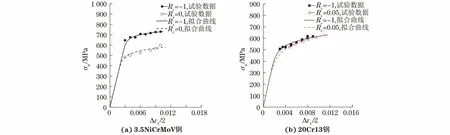
圖3 3.5NiCrMoV鋼和20Cr13鋼的循環應力幅-應變幅曲線Fig.3 Cyclic stress amplitude-strain amplitude curves of 3.5NiCrMoV steel (a) and 20Cr13 steel (b)

2.2 非對稱疲勞平均應力演變過程

由圖4可知：3.5NiCrMoV鋼和20Cr13鋼的非對稱疲勞平均應力σm演變過程相似，當最大應變較小時，初始平均應力較高，在循環過程中平均應力逐漸下降并趨于0；隨著最大應變的增大，初始平均應力降低，在循環初期下降速率較快，經數十次循環后平均應力降至0，然后進一步降至負值，最后保持平穩直至失效。

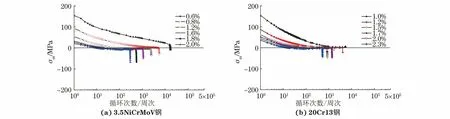
圖4 不同最大應變下3.5NiCrMoV鋼和20Cr13鋼的非對稱應變疲勞平均應力演變曲線Fig.4 Asymmetrical strain fatigue average stress evolution curves of 3.5NiCrMoV steel (a) and 20Cr13 steel (b) under different maximum strains

由圖5可知，隨著最大應變的增大，初始塑性應變Δεp增加。3.5NiCrMoV鋼在較小最大應變下的塑性應變增長緩慢，而在較大最大應變下的塑性應變增長迅速。20Cr13鋼在不同最大應變下的塑性應變增加速率相對恒定，在最大應變εmax為1.2%，1.7%，2.0%的疲勞末期出現了塑性應變降低的現象。

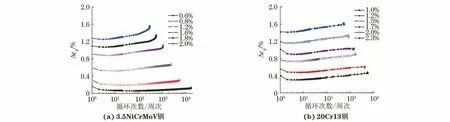
圖5 不同最大應變下3.5NiCrMoV鋼和20Cr13鋼的非對稱應變疲勞塑性應變演變曲線Fig.5 Asymmetrical strain fatigue plastic strain evolution curves of 3.5NiCrMoV steel (a) and 20Cr13 steel (b) under different maximum strains

在循環過程中塑性應變Δεp不斷累積[12]，應變循環回復到最小應變時需要提供更大的壓應力，拉應力與壓應力的相對差值減小，導致3.5NiCrMoV鋼和20Cr13鋼的非對稱應變疲勞平均應力降低。在小應變幅下試驗鋼中產生的初始塑性應變較小，此時拉應力遠大于壓應力，初始平均應力較大；隨著應變幅的增大，初始塑性應變增加，拉/壓應力差值減小，在較少循環次數下平均應力趨于0。3.5NiCrMoV鋼和20Cr13鋼均為循環軟化材料，循環過程中拉應力降低，同時塑性應變累積增加，壓應力逐漸超過拉應力，平均應力表現為負值并保持穩定直至失效。

在小應變幅條件下，3.5NiCrMoV貝氏體鋼中位錯滑移被貝氏體晶界釘扎所阻礙，塑性應變較小并平穩增長。在大應變幅條件下，貝氏體組織的滑移線快速增殖，加速了材料損傷，引發的群體短裂紋降低了材料的有效抗載能力[13]，導致疲勞過程中塑性應變快速增長，疲勞壽命明顯降低。20Cr13馬氏體鋼在循環過程中其馬氏體板條逐漸粗化，形成等軸亞晶結構，晶內位錯密度降低[8,14]，這在一定程度上緩釋了塑性變形，因此在疲勞過程中塑性應變增加速率恒定，疲勞壽命增加。

綜上可知，平均應力下降是非對稱應變控制疲勞的共同現象，下降的幅度和速率與應變幅直接相關。在平均應力下降的條件下，2種基體組織材料的非對稱疲勞壽命相對于其對稱疲勞壽命分別呈現增加和降低兩種相反結果，可知平均應力下降對疲勞壽命沒有必然影響，而由基體組織損傷機制導致的塑性應變變化是影響非對稱疲勞壽命的主要因素。

3 非對稱疲勞壽命預測

使用Manson-Coffin[2-3]模型擬合對稱應變控制疲勞數據，獲取3.5NiCrMoV鋼和20Cr13鋼的Manson-Coffin擬合參數。Manson-Coffin模型為

(1)

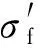
在對稱疲勞參數的基礎上通過修正或引用而建立的非對稱疲勞模型包括以下3組公式。

(1) Morrow平均應力修正公式[4]，其表達式為

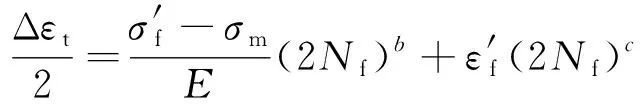
(2)

(2)SWT公式[5]，其表達式為

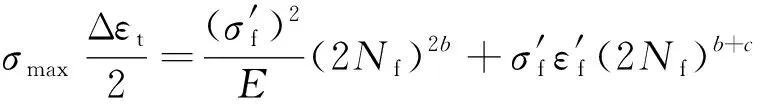
(3)

式中：σmax為循環最大應力。

(3) Ellyin總應變能密度公式[6]，其表達式為

ΔWt=Au(2Nf)γ

(4)

ΔWt=ΔWe+ΔWp

(5)

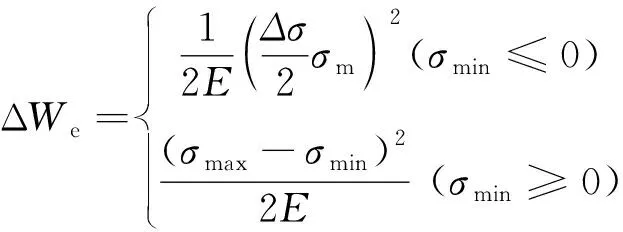
(6)

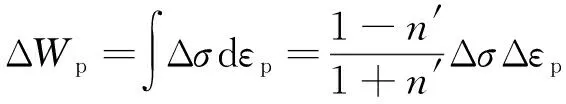
(7)

式中：ΔWt為總應變能密度；ΔWe為彈性應變能密度；ΔWp為塑性應變能密度；Δσ為應力范圍；n′為循環應變硬化指數；Au為擬合系數；γ為擬合指數；σmin為循環最小應力。

使用上述3種非對稱疲勞預測模型和Manson-Coffin對稱疲勞預測模型對3.5NiCrMoV鋼和20Cr13鋼的非對稱疲勞壽命進行預測，預測壽命Npre與試驗壽命Nob的對比結果如圖6所示。預測壽命與試驗壽命的偏離程度用分散帶Sb和標準差Es表示[11]，分散帶和標準差越小，表明預測壽命與試驗壽命的偏差越小，預測精度越高。分散帶和標準差的計算公式分別為

圖6 3.5NiCrMoV鋼和20Cr13鋼的非對稱疲勞預測壽命與試驗壽命的對比Fig.6 Comparison between prediction asymmetric fatigue life and test fatigue life of 3.5NiCrMoV steel (a) and 20Cr13 steel (b)

Sb=max(Nob/Npre，Npre/Nob)

(8)

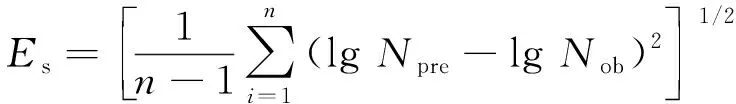
(9)

式中：n為數據點數量。

由表1可知，Morrow模型與Manson-Coffin模型的預測結果基本相同，預測壽命與試驗壽命的分散帶均超過2。3.5NiCrMoV鋼和20Cr13鋼的非對稱疲勞平均應力均趨于0，對Morrow公式的修正作用很小；Morrow模型預測精度取決于應變比對材料疲勞壽命的影響程度。3.5NiCrMoV鋼的非對稱和對稱疲勞循環應力-應變曲線差別較大，導致SWT模型預測壽命與試驗壽命間有較大的偏差，預測壽命與試驗壽命的分散帶為3.472；20Cr13鋼的非對稱和對稱疲勞循環應力-應變曲線相近，其SWT模型的預測壽命偏差相對較小，預測壽命與試驗壽命的分散帶為2.001。Ellyin總應變能密度公式引入了平均應力修正和對稱疲勞的硬化指數，其中平均應力修正效果可忽略。Ellyin模型對3.5NiCrMoV鋼非對稱疲勞壽命的預測效果在Morrow模型和SWT模型之間，而20Cr13鋼的Ellyin模型預測壽命的分散帶小于2，標準差相對最小。由此可知，Ellyin模型對20Cr13鋼非對稱疲勞壽命的預測效果較好。由圖3可以看出，3.5NiCrMoV鋼的對稱與非稱循環硬化趨勢相差較大，而20Cr13鋼的對稱與非對稱循環硬化趨勢相似。

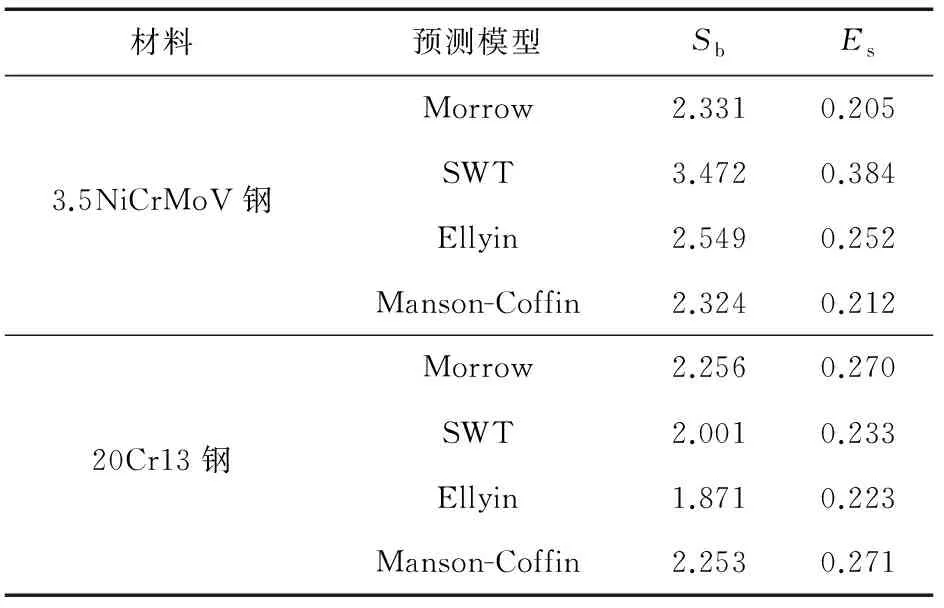
表1 非對稱疲勞壽命預測能力評估結果

綜上可知：對于平均應力趨于0的非對稱應變疲勞壽命預測，基于修正平均應力的Morrow模型與對稱疲勞Manson-Coffin模型的預測效果基本相同，其預測精度取決于應變比對疲勞壽命的影響；基于力學參量的SWT模型不適用于非對稱與對稱疲勞循環應力-應變曲線相差較大的貝氏體基體3.5NiCrMoV鋼的非對稱疲勞壽命預測；Ellyin模型對循環硬化趨勢相近的20Cr13鋼的非對稱疲勞壽命具有較好的預測效果。

4 結 論

(1) 在相同應變幅下，貝氏體基體3.5NiCrMoV鋼的非對稱疲勞壽命不高于對稱疲勞壽命，馬氏體基體20Cr13鋼的非對稱疲勞壽命高于對稱疲勞壽命；在相同應變幅下，貝氏體基體3.5NiCrMoV鋼的對稱和非對稱循環應力相差較大，而馬氏體基體20Cr13鋼的對稱和非對稱循環應力相近。

(2) 平均應力下降是非對稱應變控制疲勞的共同現象，下降的幅度和速率與控制應變幅直接相關。平均應力下降對疲勞壽命沒有必然影響，由基體顯微組織損傷機制導致的塑性應變變化是影響非對稱疲勞壽命的主要因素。

(3) 3.5NiCrMoV鋼和20Cr13鋼的非對稱疲勞平均應力均趨于0，基于修正平均應力的Morrow模型與對稱疲勞Manson-Coffin模型的疲勞壽命預測效果基本相同，其預測精度取決于應變比對疲勞壽命的影響。基于力學參量的SWT模型不適用于非對稱與對稱疲勞循環應力-應變曲線相差較大的貝氏體基體3.5NiCrMoV鋼的疲勞壽命預測。Ellyin模型對非對稱與對稱循環硬化趨勢相近的20Cr13鋼的非對稱疲勞壽命具有較好的預測效果。