基于加權特征投影的信源數估計方法
王 純,高于晰
(西安建筑科技大學 信息與控制工程學院,西安 710055)
0 引言
波達方向(DOA,direction of arrival)估計作為陣列信號處理的重要研究方向在雷達、通信、聲吶和生物醫學等眾多領域有至關重要的地位[1]。而絕大多數基于子空間類的算法需要已知信號源的數目,若信源數目出現欠估計或過估計,將直接影響DOA估計的結果[2-3]。故準確的信源數估計是DOA估計的先決條件。并且在實際應用中,由于系統對實時性的要求和陣列各陣元間的相關性,導致采樣數有限和色噪聲的干擾,傳統針對白噪聲的信源數估計方法在該背景下往往失效,因此研究色噪聲/低快拍下的信源數估計方法具有十分重要的意義。
常見的信源數估計方法包括特征值分解法、信息論方法[4-7]、蓋氏圓方法(GDE,gerschgorin’s disks estimation)[8-10]和正則相關技術[11]、使用深度學習的方法[12]。特征值分解法是通過信號特征值與噪聲特征值的大小差異,并結合階躍準則實現信源數估計,計算簡單且準確度較高,但不適用于低快拍、低信噪比和色噪聲條件。采用深度學習[12]的信源數估計方法能夠在特定條件下取得很好的效果,然而當環境變化就需要重新對網絡進行訓練,因此實用性有限。基于信息論的信源個數估計方法[7]包括Akaike信息論準則(AIC,akaike information theoretic criter)、最小描述長度準則(MDL,minimum description length criterion)等計算量小,能很好地應用于白噪聲條件,但在色噪聲條件下往往失效。近年來,學者對色噪聲背景下的信源數估計進行了相關研究。文獻[13]將對角加載技術用于信息論信源數估計方法,較好地改善了算法在色噪聲條件下的估計性能,而加載量的不同在一定程度上會對算法穩定性產生影響。正則相關技術[11]也可用于色噪聲條件,但需要兩個空間分離的陣列,大大降低了陣列的有效孔徑,實際工程使用性不強。文獻[14]利用對數函數對特征值進行擬合,改善了特征值的發散程度,而擬合函數參數的固定在一定程度上降低了算法的魯棒性。蓋氏圓信源數估計方法沒有限定噪聲模型,因此可以應用于白噪聲與色噪聲環境,但是在低快拍和低信噪比條件下成功估計概率降低,且該算法在酉變換過程中犧牲了一個自由度,使得計算過程產生的特征向量無法使用于后續的DOA估計。文獻[15]在蓋氏圓方法的基礎上進行了升維處理,節省了一個自由度,但要對蓋氏圓半徑經過M-1次擬合計算量較大,且在低快拍條件下性能有所下降。
在此基礎上,本文通過對數據協方差矩陣在色噪聲/低快拍條件下的分析,提出了一種基于加權特征投影的信源數估計方法。該方法在降噪數據協方差矩陣特征值的基礎上引入信號子空間與噪聲子空間的正交性,構建了加權空間矩陣,并將降噪后的協方差矩陣在該空間上進行投影,利用投影得到的結果構建判決函數,進而實現信源數估計。
1 信號模型
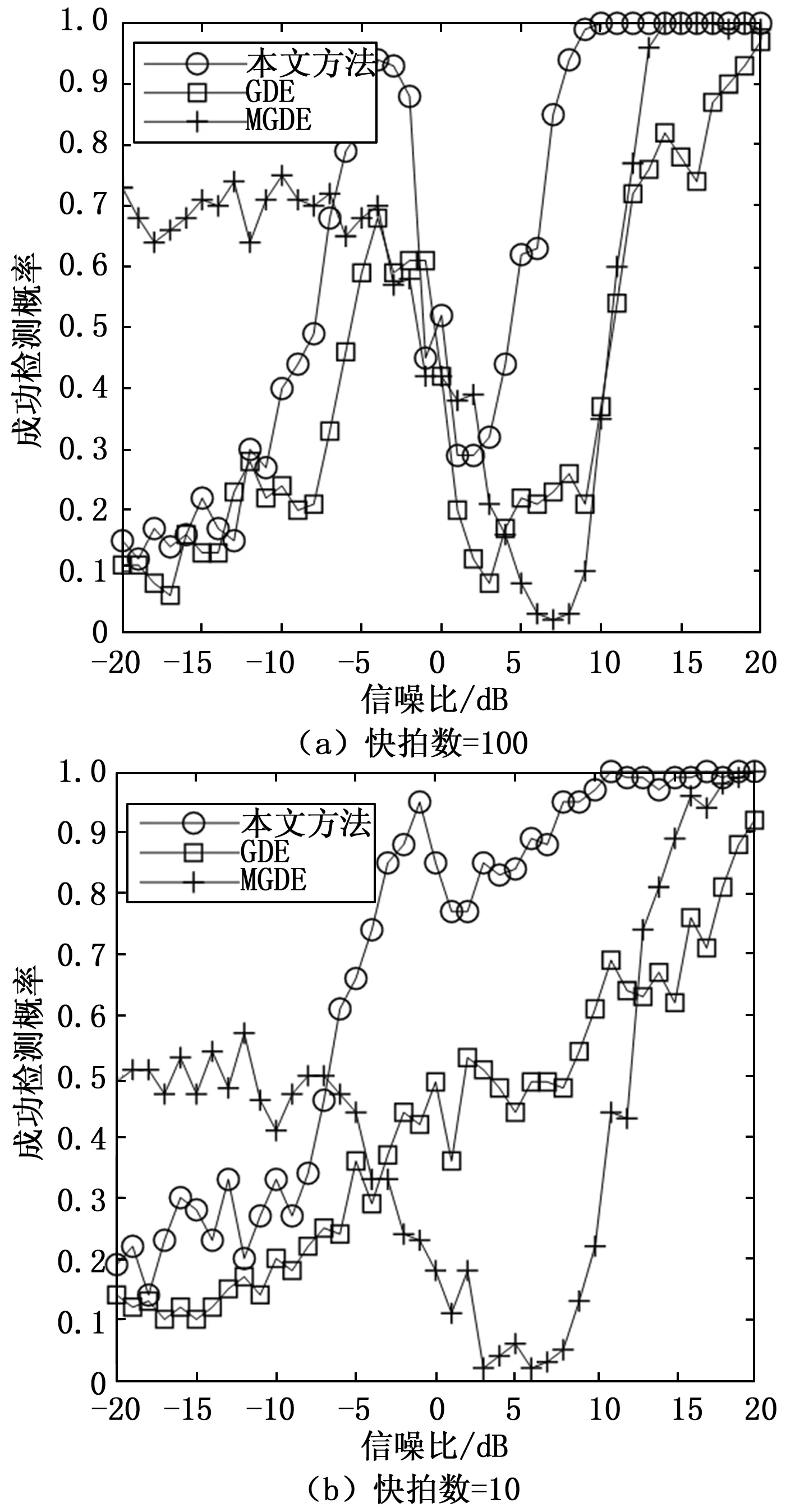
假設一M元均勻放置的天線陣列,陣元間距為半波長,有K個遠場窄帶不相干的信號從(θ1,θ2,θ3,…,θK)入射到陣列(K X(t)=A(θ)*S(t)+N(t) (1) 式中,S(t)=[s1(t),s2(t),…,sK(t)]T為K×1維的信號矩陣;N(t)=[n1(t),n2(t),…,nM(t)]T為維噪M×1聲向量;A(θ)=[a(θ1),a(θ2),…a(θK)]為M×K維的陣列導向矢量陣,其中a(θi)(i=1,2,…,K)為各信號的導向矢量,具體表達式如下: (2) 假設信號與噪聲相互獨立,陣列接收數據協方差矩陣為: RX=E[X(t)XH(t)]=ARSAH+RN (3) 式中,RS=E[S(t)SH(t)]為信號協方差矩陣;RN=E[N(t)NH(t)]為噪聲協方差矩陣。 對陣列接收數據的協方差矩陣RX進行特征分解,可得: RX=U∑UH (4) 式中,∑=diag(λ1,λ2,…,λM)為特征值構成的對角陣且滿足λ1≥λ2≥…≥λM;特征值對應的特征向量構成矩陣U=[e1,e2,…eM]。 色噪聲是由各個陣元間的互耦和噪聲的相關性,以及各通道內部噪聲功率的不同所產生的。其噪聲協方差矩陣不再是一個對角陣(與白噪聲相比),同時數據協方差矩陣的噪聲特征值不再圍繞噪聲功率分布,導致噪聲特征值的發散,進而影響到利用特征值進行信源數估計的相關算法的性能。 通常,數據協方差矩陣展開可得: RX=E[X(t)XH(t)]= ARSAH+2Re(RSN)+RN (5) 實際中,往往采用以下有限次快拍的數據采樣協方差矩陣逼近RX: (6) 而當快拍數有限時,數據協方差矩陣的交叉項不再為0,RSN≠0,RN不再為對角陣。因此,有限快拍數增加了信號之間、信號與噪聲之間以及各陣元噪聲之間的相關性。那么,在色噪聲/低快拍條件下,如果直接使用協方差矩陣的特征值進行信源數估計,估計性能不佳。接下來,將在特征值的基礎上引入信號子空間與噪聲子空間的正交性,提出一種基于加權特征投影的信源數估計方法。 預將陣列接收協方差矩陣RX用分塊的形式表達,先將陣列導向矢量A按行分塊可寫作: (7) 其中: (8) 則陣列接收的數據協方差矩陣可以表示為[16]: (9) 由于信源均互不相關,且RS為滿秩的對角陣,故RSbi≠0(i=1,2,…,M)。 在實際應用中,為了保證算法在低信噪比條件下的性能,首先對陣列接收數據協方差矩陣進行預處理。因受快拍數低的影響,噪聲所對應的小特征值為非零的較小值,可以選取最小的兩個特征值的均值對陣列接收數據的協方差矩陣進行降噪處理,得到新的協方差矩陣: (10) 式中,I為M×M的單位陣。 然后,對降噪后的協方差矩陣進行特征分解: (11) 式中,∑′=diag(μ1,μ2,…,μM)為特征值構成的對角陣;U′=[ξ1,ξ2,…,ξM],ξi(i=1,2,…M)為特征值μi對應的特征向量。將特征值作為對應特征向量的權值,構造了加權空間矩陣G,表達如下: G=U′∑′= [ξ1,ξ2,…,ξM]·diag(μ1,μ2,…,μM)= [μ1ξ1,μ2ξ2,…,μMξM] (12) G是通過特征值μi對特征空間U′進行加權變換得到的加權空間矩陣。 (13) ri=|ρi| =|μiHξiHARSbjH|≤|μiH||ξiHA||RSbjH| = k|μiH||ξiHA|→0(j=1,2,…,M) (14) ri=|ρi| =|μiHξiHARSbjH|≤|μiH||ξiHA||RSbjH| = k|μiH||ξiHA| >0(j=1,2,…,M) (15) 基于以上理論研究和矩陣分析,進行信源數估計,首先定義函數: (16) 式中,k取1,2,…,M,即(13)式中每一行中各元素先開方后求其均值。構造判決函數: (17) 式中,L為快拍數,D(L,M)是一個與陣元數和快拍數有關的調整因子,它在0至1之間選取,與陣元數和快拍數均成正比,陣元數和快拍數越多D(L,M)的取值越接近于1。k取1,2,…,M,所有使Δ(k)>0的f(k)個數即為信源數目。 步驟1:計算陣列接收數據協方差矩陣:RX=E[X(t)XH(t)]; 步驟3:對新協方差矩陣進行特征分解,根據式(12)利用得到的特征值和特征向量構造空間矩陣G; 步驟5:根據式(16),求出M個函數值f(k); 本算法通過對原協方差矩陣進行降噪預處理,該步驟可以降低噪聲判據值,從而使算法應用于低信噪比環境中;本方法沒有對噪聲模型進行特定限制,可應用于色噪聲背景下。特別是在劃分噪聲和信號時,本文提出了進一步縮小噪聲的判據值和放大信號的判據值的方法,具體說明如下: 本文方法的計算量包括:對M階協方差矩陣進行特征分解的計算量約為M3;對M階去特征的協方差矩陣進行特征分解的計算量約為M3;加權投影部分計算量為2M3,故本文方法的總體計算量為4M3。而經典的GDE算法的計算量集中在M-1階矩陣特征分解和M階矩陣酉變換部分。改進蓋氏圓算法(MGDE,modified gerschgorin’s disks estimation)與GDE算法相比增加了一次酉變換的計算量。信息論方法的計算量主要集中在M階協方差矩陣的特征分解和似然函數[7]的計算。如表1所示,將本文方法與信息論方法、GDE算法以及MGDE算法的算法復雜度進行了對比。本文方法計算復雜度略低于MGDE算法,但高于信息論方法和GDE算法。對比信息論算法和GDE算法,本文方法計算復雜度的提升換來了在兩種噪聲背景下及低快拍、低信噪比條件下的性能提升。 表1 算法復雜度對比 實驗設置:仿真采用陣元間距為半波長的7陣元均勻線陣(理論最大檢測信源數為6),信源數分別設定為為2個和5個信源,在不同信噪比和快拍下進行200次Monte-Carlo實驗,通過成功檢測信源數目的概率評價算法性能。 為了驗證本文提出算法的有效性,實驗在白噪聲條件下與AIC準則、MDL準則、GDE準則、MGDE算法和文獻[15]算法進行仿真對比,分析不同條件下的算法性能。 實驗一:陣元數為7時,在白噪聲條件下,依次給出多快拍和低快拍兩種情況的信源數目成功檢測概率隨信噪比的變化情況。仿真條件如下:快拍數分別為100和10,有2個獨立信源,分別由-10°和0°入射到7陣元的均勻線陣,陣元間距為半波長,得到成功檢測概率隨信噪比的變化情況。 多快拍條件下,實驗結果如圖1(a)所示,可以看出4種算法的成功檢測概率均隨SNR增大而增大。其中本文算法在信噪比大于-3 dB時信源數成功檢測概率達到100%,MDL準則在信噪比為0 dB時信源數成功檢測概率達到100%,MGDE算法在信噪比大于1 dB時信源數成功檢測概率達到100%,文獻[15]的算法在信噪比大于8 dB時,成功檢測概率接近100%,AIC準則和GDE準則均低于本文算法,可見本文算法性能在低信噪比條件下略優于AIC準則、MDL準則、MGDE算法、GDE準則和文獻[15]算法;低快拍條件下,實驗結果如圖1(b)所示,可以看出信息論算法受快拍數影響大,性能下降較快。本文算法在信噪比大于2 dB時信源數成功檢測概率達到100%,明顯高于GDE準則、MGDE算法和文獻[15]算法。可見,本文算法在多快拍和低快拍兩種情況下都優于其他5種算法。 圖1 信源數為2時,白噪聲條件下,成功檢測概率隨SNR變化 實驗二:陣元數不足時,在白噪聲條件下,依次給出多快拍和低快拍兩種情況的信源數目成功檢測概率隨信噪比的變化情況。仿真條件如下:快拍數分別為100和10,有5個獨立信源,分別由-25°、-10°、0°、10°和25°入射到7陣元的均勻線陣,陣元間距為半波長,得到成功檢測概率隨信噪比的變化情況。 多快拍條件下,實驗結果如圖2(a)所示,可以看出本文方法的成功檢測概率達到100%時的信噪比為9 dB,MDL準則大于8 dB時其成功檢測概率近似達到100%但略有波動,文獻[15]算法成功檢測概率達到100%時信噪比為10 dB但略有波動,AIC準則、MGDE算法和GDE準則其檢測性能明顯低于本文算法;低快拍條件下,實驗結果如圖2(b)所示,可以看出當信噪比大于16 dB時,本文算法成功檢測概率達到100%,文獻[15]算法當信噪比大于16 dB時,成功檢測概率達到100%但略有波動,而AIC準則、MDL準則、MGDE算法和GDE準則還未達到。 圖2 信源數為5時,白噪聲條件下,成功檢測概率隨SNR變化 實驗三:陣元數一定時,在白噪聲條件下,為檢測算法在不同信源個數下的估計性能,給出了成功檢測概率隨信源個數的變化情況。仿真條件如下:陣元數為7,快拍數取100,信噪比為15 dB,信源數分別取1至6,信源為來自不同方向的獨立信源,得到成功檢測概率隨信源數變化的情況。 實驗結果如圖3所示,信源數為1至5時,本文方法、MGDE算法、MDL準則成功檢測概率為100%,GDE準則近似100%,AIC準則與文獻[15]算法均未達到100%。信源數為6時,AIC準則成功檢測概率接近50%,其余5種算法均接近0。可以看出本文方法,犧牲了自由度換取了在不同信源個數條件下較高的成功檢測概率。 圖3 白噪聲條件下,成功檢測概率隨信源數變化 實驗四:陣元數充足時,在色噪聲條件下,依次給出多快拍和低快拍兩種情況的信源數目成功檢測概率隨信噪比的變化情況。各陣元產生的色噪聲是由高斯白噪聲激勵一個穩定的ARMA模型產生的[17]。仿真條件如下:快拍數分別為100和10,有2個獨立信源,分別由-10°和0°入射到7陣元的均勻線陣,陣元間距為半波長,得到成功檢測概率隨信噪比的變化情況。 多快拍條件下,實驗結果如圖4(a)所示,可以看出當信噪比為6 dB時本文算法成功檢測概率達到100%,MGDE算法當信噪比為9 dB時成功率達到100%,GED準則當信噪比大于16 dB時成功檢測概率為100%;低快拍條件下,實驗結果如圖4(b)所示,可以看出當信噪比為9 dB時本文算法成功檢測概率達到100%,MGDE算法當信噪比為15 dB時成功率達到100%,GED準則當信噪比大于16 dB時成功檢測概率為100%。可見,在色噪聲條件下,本文算法優于MGED算法和GED準則。 圖4 信源數為2時,色噪聲條件下,成功估計信源數隨SNR變化 實驗五:陣元數不足時,在色噪聲條件下,依次給出多快拍和低快拍兩種情況的信源數目成功檢測概率隨信噪比的變化情況。同樣各陣元產生的色噪聲是由高斯白噪聲激勵一個穩定的ARMA模型產生的[24]。仿真條件如下:快拍數分別為100和10,有5個獨立信源,分別由-25°、-10°、0°、10°和25°入射到7陣元的均勻線陣,陣元間距為半波長,得到成功檢測概率隨信噪比的變化情況。 多快拍條件下,實驗結果如圖5(a)所示,可以看出當信噪比為10 dB時本文算法成功檢測概率達到100%,MGED算法在信噪比為14 dB時成功率達到100%,GED準則在信噪比為20 dB時仍未達到100%;低快拍條件下,實驗結果如圖5(b)所示,可以看出當信噪比大于11 dB時本文算法成功檢測概率接近100%且略有波動,MGED算法在信噪比為18 dB時成功率接近100%,GED準則當信噪比為20 dB時仍未達到100%。可見,在色噪聲條件下,本文算法優于MGED算法和GED準則。 圖5 信源數為5時,色噪聲條件下,成功估計信源數隨SNR變化 實驗六:陣元數一定時,在色噪聲條件下,為檢測算法在不同信源個數下的估計性能,給出了成功檢測概率隨信源個數的變化情況。仿真條件如下:陣元數為7,快拍數取100,信噪比為15 dB,信源數分別取1至6,信源為來自不同方向的獨立信源,得到成功檢測概率隨信源數變化的情況。 實驗結果如圖6所示,信源數為1至5時,本文方法成功檢測概率為100%,信源數為6時成功檢測概率下降至0。GDE準則和MGDE算法當信源數變為4時,成功檢測概率下降,信源數為6時,成功檢測概率下降至0。 圖6 色噪聲條件下,成功檢測概率隨信源數變化 本文提出了基于加權特征投影的信源數估計方法,利用降噪后協方差矩陣的特征值和特征向量構建了加權空間矩陣,通過空間投影使得信號判據值遠大于噪聲判據值,最后通過構建判決函數實現信源數估計。通過理論分析證明了該方法的可行性,并分別在白噪聲和色噪聲兩種情況下進行仿真實驗,結果表明本文算法受陣元數目影響較小,且在低快拍、低信噪比條件下也具有優良的估計性能,更適于工程應用。2 基于加權特征投影的信源數估計方法
2.1 陣列接收協方差矩陣分塊表達
2.2 加權空間矩陣的構建
2.3 判據值的縮放




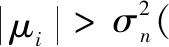

2.4 信源數估計方法
3 算法步驟


4 算法性能分析說明


5 算法復雜度分析

6 仿真實驗
6.1 白噪聲條件下仿真分析



6.2 色噪聲條件下仿真分析


7 結束語

