兩次淬火下橫場中XY鏈的動力學量子相變*

符浩 曹凱源 鐘鳴 童培慶2)?

1)(南京師范大學物理科學與技術學院,南京 210023)

2)(南京師范大學,江蘇省大規模復雜系統數值模擬重點實驗室,南京 210023)

研究了兩次淬火下橫場中XY 鏈的動力學量子相變.兩次淬火是指系統的Hamilton 量先由H0 淬火到H1,演化一段時間T 后再由H1 淬火到H2.由于橫場中XY 鏈存在兩種不同的量子相變(Ising 相變和各向異性相變),因此主要討論淬火路徑對橫場中XY 鏈的動力學量子相變的影響,發現第2 次淬火后系統發生動力學量子相變的臨界時間存在三種典型的情形.情形I 對應于臨界時間在一定的T 范圍內出現,它與由H0 淬火到H1的臨界時間相聯系.情形II 對應于臨界時間在任意T 時總是出現,它與由H0 直接淬火到H2的臨界時間相聯系.情形III 對應于臨界時間也在任意T 時總是出現,它同時與由H0 淬火到H1 以及由H0 直接淬火到H2的臨界時間相聯系.還發現兩次淬火都經過同一類相變點時,第2 次淬火后只會出現情形I 對應的臨界時間.而兩次淬火經過不同類相變點時,第2 次淬火后的臨界時間會出現上述三種情形中的任意兩種,它與淬火路徑有關.

1 引 言

近年來,隨著理論方法和計算機技術的提高以及實驗技術的發展,孤立量子系統的動力學行為得到了廣泛研究,取得了迅速的進展[1–7].在眾多的動力學行為中,動力學量子相變是最近非常活躍的研究課題之一[8–55].動力學量子相變最早是Heyl等[8]在研究淬火下量子Ising 鏈的動力學行為時發現的.它描述了Loschmidt 振幅隨時間演化的奇異性,借助于Loschmidt 振幅與統計物理中的配分函數的相似性,研究發現出現奇異性的時間對應于復時間平面中的Fisher 零點與虛軸的交點[8–11].隨后,人們在許多不同的量子系統中都發現了動力學量子相變,這些系統包括XY鏈[9,16]、Kitaev 蜂窩模型[17]、XXZ鏈[18]、ANNNI 鏈[19,20]、非均勻電子系統[21,22]、非均勻自旋系統[11]、長程相互作用系統[23]、量子Potts 鏈[24]、非厄米格點系統[25,26]、Bose-Einstein 凝聚體[27]、cross-stitch 平帶網絡[28]和有限溫系統[29]等.除了在研究淬火下的動力學行為以外,人們也研究了線性退火[10]與周期Floquet[32]系統的動力學行為.此外,在實驗方面,例如捕獲離子模擬[33]、動力學渦旋觀測[34]、量子模擬器觀測[35,36]、核磁共振模擬[37]、單光子量子行走[38]和自旋量子凝聚[39]等,也觀察到了動力學量子相變.

最近,Kennes 等[40]研究了兩次淬火下橫場中量子Ising 鏈和ANNNI 鏈的動力學量子相變.他們發現系統在兩次淬火均經過Ising 相變點(即從順磁相淬火到鐵磁相,然后再淬火到順磁相)的情形時,系統第2 次淬火后的動力學量子相變現象的出現與否取決于兩次淬火之間的時間間隔,從而可以通過調節兩次淬火之間的時間間隔來調控動力學量子相變.這提供了一種調控系統的動力學行為的新思路.由于橫場中量子Ising 鏈的特殊性,他們只討論了兩次淬火均經過Ising 相變點的淬火路徑.眾所周知,橫場中的量子Ising 鏈是橫場中XY鏈的一種特殊情形,而XY鏈的相圖要比量子Ising 鏈的相圖豐富得多,不僅存在從鐵磁相到順磁相的Ising 相變,還存在從x方向的鐵磁相到y方向的鐵磁相的各向異性相變.另一方面,一次淬火下橫場中XY鏈的動力學量子相變與淬火的路徑有關,如當淬火經過各向異性相變時,它會出現兩個特征臨界時間.因此,本文主要研究兩次淬火的路徑以及淬火間時間間隔對橫場中XY鏈的動力學量子相變的影響.

本文第2 節給出了橫場中XY鏈經過兩次淬火的計算方法.第3 節中就不同的淬火路徑分別進行了討論,給出了不同淬火路徑和時間間隔對XY鏈在兩次淬火下的動力學量子相變的影響.最后總結了第2 次淬火后的臨界時間與淬火路徑的依賴關系.

2 模型和計算方法

本文研究的淬火過程如下:假設系統在t<0時處在H0的基態|ψ0〉上.在t=0時,系統經過第1次淬火后,Hamilton量由H0變到H1,然后在H1下演化一段時間T.在t=T時,系統經過第2次淬火,Hamilton量由H1變到H2后,隨時間的演化.這里的T為兩次淬火之間的時間間隔.系統含時Hamilton 量為

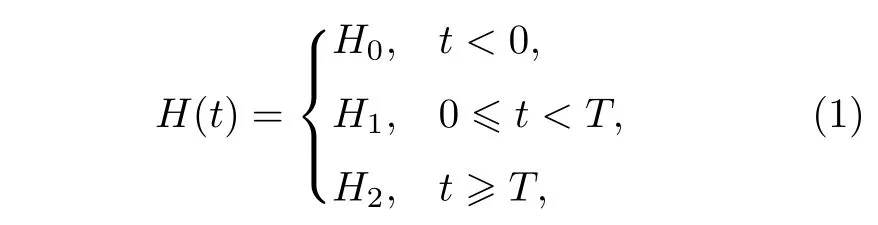
本文研究的系統是一般的橫場中XY鏈,其Hamilton 量可寫成

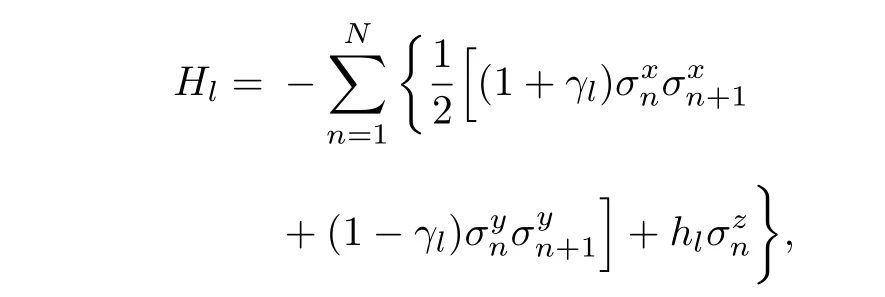
其中,l=0,1,2 分別對應于(1)式中的3個Hamilton量,它們的形式是一樣的,差別是具有不同的各向異性參數γl(l=0,1,2)和外場hl(l=0,1,2) .這里是第n個格點上的Pauli 矩陣.特別地,當γl=±1 時,系統對應于橫場中Ising 鏈.通過Jordan-Wigner 變換、Fourier 變換和Bogoliubov 變換[56],可以解析地得到

上面的結果同樣可以從對Fisher 零點的討論中得到.借助于Loschmidt 振幅與統計物理中的配分函數之間的相似性,令(4)式中 it=z,然后研究Loschmidt 振幅G(z) 在復z平面上的零點(也被稱為Fisher 零點).在熱力學極限下,如果Fisher零點與虛軸 R e(z)=0 相交,則其交點對應于發生動力學量子相變的時間.Fisher 零點對應Loschmidt振幅為0的點,即gk(z)=0,由(6)式和文獻[8]可知Fisher 零點如下:

這里(9a)式對應于第1 次淬火(H0→H1)時的Fisher 零點,而(9b)式對應于第2 次淬火后的Fisher 零點.公式中的n是整數,每個n給出了一支Fisher 零點.給定n之后,對于每1 個k有1 個zk與之對應,所以這里給出了一系列Fisher 零點.當存在某個k=k?(k?為臨界動量)使得|Bk?/Ak?|=1,則zk?就在虛軸上,它對應于兩次淬火后的臨界時間如下:

其中t?=π/(2ε2,k?) 被稱為特征臨界時間.如果系統中存在兩個以上k?滿足|Bk?/Ak?|=1,那么會出現多個特征臨界時間.這些臨界時間隨t周期性出現,并且系統中存在幾個特征臨界時間就有幾個不同的周期重合在一起.從(10)式可以看出它與一次淬火時不一樣[8,9],會多出1 個因子.

另一個描述動力學量子相變的物理量是率函數λ(t) .它的定義為

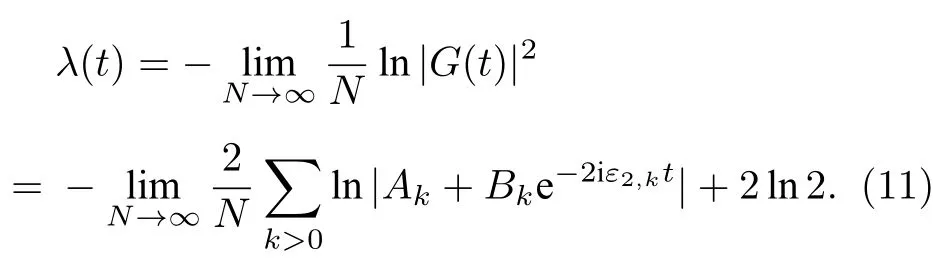
在臨界時間,率函數是奇異的.

3 結果和討論

圖1 給出了橫場中XY鏈在h≥0時的相圖.圖中的實線h=1,?1≤γ≤1上的點是Ising相變點,而0≤h≤1,γ=0 上的點是各向異性相變點.這兩條臨界線把參數空間分成3 個區域,其中PM 表示順磁相,FMx表示x方向的鐵磁相,FMy表示y方向的鐵磁相.我們所討論的系統的淬火主要是通過改變外場和各向異性參數來實現.

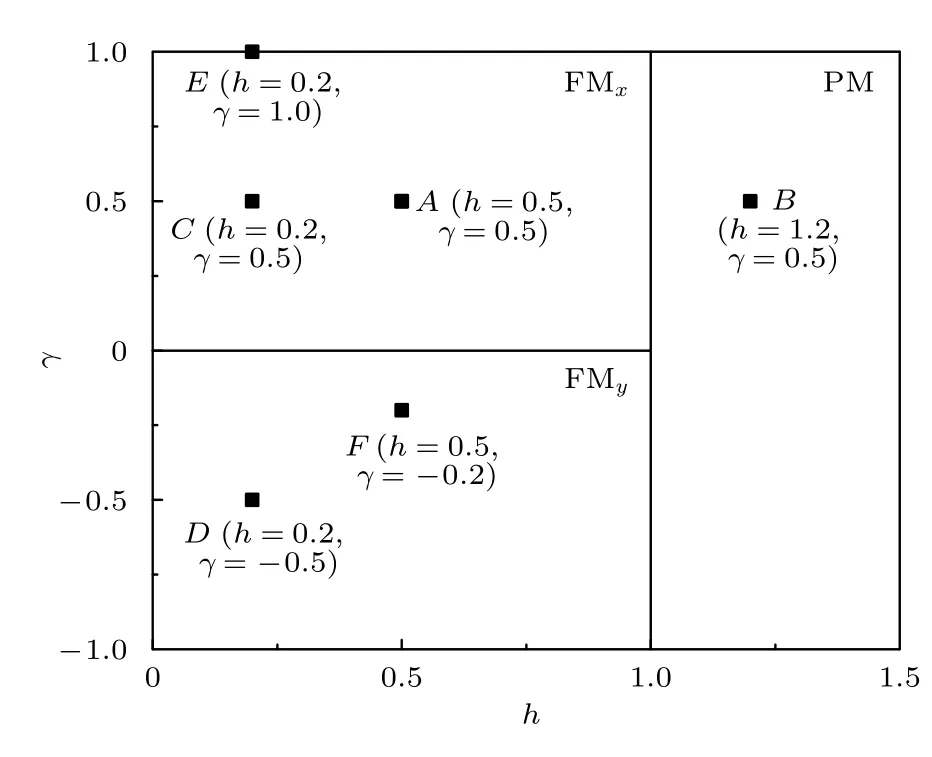
圖1 橫場中XY 鏈的相圖,其中的點 A ,B,···,F 表示典型的參數值所對應的位置Fig.1.Phase diagram of the X Y chain in a transverse field.The points A ,B,···,F in the phase diagram correspond to the typical parameter values.

為了方便起見,我們用A,B,···,F標記相圖中典型的參數值(γ,h) 所對應的位置.用符號A →B →C表示系統從A淬火到B后,再淬火到C的過程,即點A,B和C的參數值分別對應于(1)式中的H0,H1和H2中的外場和各向異性參數,其他的情形是類似的.在下面的討論中,將研究兩類典型的情形.一類是經過同一類量子相變點的兩次淬火,其中包括經過Ising 相變點(如A →B →C)和經過各向異性相變點(如C→D →E)的情形.另一類是經過不同類量子相變點的兩次淬火,其中包括先經過Ising 相變點再經過各向異性相變點(如B→C →D)、先經過各向異性相變點再經過Ising 相變點(如D→C →B) 以及先經過Ising相變點后同時經過Ising 和各向異性相變點(如C →B →D)的情形.下面具體討論這五種典型的情形.

3.1 兩次淬火經過同一類相變點

3.1.1 均經過Ising 相變點的兩次淬火

首先討論均經過Ising 相變點(A→B →C)的兩次淬火情形.T-t平面內的臨界時間在圖2(a)中給出.圖中的實線描述了臨界時間與時間間隔T的關系.在圖中的兩條虛線分別對應于T=0.5,1.0.相應的Fisher 零點分別在圖2(b1)和圖2(b2)中給出.而相應的率函數隨時間t的變化在圖2(c)中給出.

圖2 (a)淬火路徑A→B→C對應的臨界時間圖,圖中兩條虛線對應的時刻分別為T=0.5和1.0;(b1)T=0.5和(b2)T=1.0且t>T 時的Fisher 零點分布;(c)兩次淬火過程中的率函數,黑色和紅色實線分別對應 T =0.5 和 1 .0 ;(d) |Bk/Ak|與k的關系,黑色和紅色實線分別對應 T =0.5 和1.0Fig.2.(a) Location of the critical times in the t -T plane for the path A →B →C .The dotted lines mark the times for T=0.5 and 1 .0 ,respectively.(b) The Fisher zeros for t >T with(b1) T =0.5 and(b2) T =1.0,respectively.(c) The rate functions corresponding to T =0.5 and 1 .0 ,respectively.(d) The relationship between | Bk/Ak| and k for T =0.5 and 1 .0,respectively.

從圖2(a)可以看出,當TT2時,由于此時的時間間隔大于了第1 次淬火后的特征臨界時間,故第2 次淬火前會出現動力學量子相變.在T2T4后,系統第2 次淬火前會出現動力學量子相變,但是第2 次淬火后的動力學量子相變將會循環出現前面的情形.

下面分析系統在第2 次淬火后出現動力學量子相變的原因.根據前面的討論,圖2(d)給出了|Bk/Ak|與k的關系,圖中的黑色和紅色實線分別對應于T=0.5 和T=1.0 .從圖2(d)可以看出:當T=0.5 時,對于任意k均滿足|Bk/Ak|<1,因此系統不存在動力學量子相變.而當T=1.0 時,出現兩個k?使得|Bk?/Ak?|=1,它們分別對應于圖2(b2)中Fisher 零點與虛軸的兩個交點(每個n).此時系統存在動力學量子相變.

這說明當淬火路徑為A→B →C時,第2 次淬火后的動力學量子相變的出現與否取決于兩次淬火之間的時間間隔T.這與橫場中量子Ising 鏈[40]的情形是類似的.

3.1.2 均經過各向異性相變點的兩次淬火

其次討論均經過各向異性相變點(C →D →E)的兩次淬火情形.圖3(a)給出了T-t平面內的臨界時間.同樣地,可以看出當T比較小時,第1 次淬火后不出現動力學量子相變,第2 次淬火后只有在一定T的范圍內會出現動力學量子相變.當T大于第1 次淬火后的較小的特征臨界時間T5時,第2 次淬火前只有1 個臨界時間,而當T大于第1 次淬火后的較大的特征臨界時間T6時,第2 次淬火前有兩個臨界時間.在這個過程中,第2 次淬火后始終有動力學量子相變.隨著T的繼續增大,第2 次淬火之后的動力學量子相變會消失,然后循環出現前面的情形.作為1 個例子,給出了T=1.25(對應于圖3(a)中的虛線)時由(9b)式給出的Fisher 零點(如圖3(b))和率函數(如圖3(c)).從圖3(c)可看出,當t<2.5 時率函數有3 個奇異點,分別對應于圖3(a)中的①到③.其中點②和③的臨界時間對應于圖3(b)中n=1的Fisher 零點與虛軸的交點.而點①的臨界時間是對應于(9a)式所示的Fisher 零點與虛軸的交點(沒有給出).

在一次淬火中,經過各向異性相變點與經過Ising 相變點不同,它會出現兩個特征臨界時間.每個特征臨界時間所對應的兩次淬火后的一支臨界時間線與前面討論的臨界時間線相類似.為了進一步理解第1 次淬火后出現的臨界時間與第2 次淬火后出現的臨界時間之間的聯系,圖3(d)給出了(9a)式中 t an2(θ0,k ?θ1,k)/2 以及在T=T5,T6時(9b)式中|Bk/Ak|隨動量k的變化.當tan2(θ0,k ?θ1,k)/2=1(即圖中的黑色實線與點線的交點)時對應的橫坐標k1和k2為兩個特征動量,它們對應了一次淬火后經過各向異性相變點時的兩個特征時間.我們發現,當T=T5≈1.1574 時|Bk/Ak|=1(即圖中的紅色實線與虛線的交點處)時對應的動量與k1重合,這表明圖中左起第1 條的藍色臨界時間線是跟第1 次淬火后的第1 條臨界時間線相聯系.而當T=T6≈1.3879 時|Bk/Ak|=1(即圖中的藍色實線與虛線的交點)對應的動量與k2重合,這表明圖中左起第2 條的藍色臨界時間線是跟第1 次淬火后的第2 條臨界時間線相聯系.

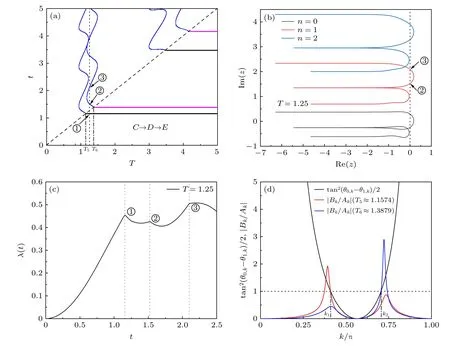
圖3 (a)淬火路徑 C →D →E 對應的臨界時間圖,圖中虛線對應的時刻為 T =1.25 ;(b) T =1.25 且 t >T 時的Fisher 零點分布;(c) T =1.25 時兩次淬火過程的率函數;(d)黑色實線是 t an2(θ0,k -θ1,k)/2 與k的關系,圖中紅色和藍色實線為|Bk/Ak|與k的關系,對應的時間間隔分別為 T =T5 ≈1.1574 和T=T6 ≈1.3879Fig.3.(a) Location of the critical times in the t -T plane for the path C →D →E .The dotted line marks the time for T =1.25 .(b) The Fisher zeros for t >T with T =1.25 .(c) The rate function corresponding to T =1.25 .(d) The black line corresponding to the relationship between t an2(θ0,k -θ1,k)/2 and k.The red and blue lines corresponding to the relationships between|Bk/Ak| and k for T =T5 ≈1.1574 and T =T6 ≈1.3879,respectively.

3.2 兩次淬火經過不同類相變點

3.2.1 先經過Ising 相變點再經過各向異性相變點的兩次淬火

下面討論先經過Ising 相變點再經過各向異性相變點(B→C →D)的兩次淬火情形.圖4(a)中給出了T-t平面內的臨界時間.與前面不同的是,可以看出在第2 次淬火后系統中會出現兩種類型的臨界時間線.一種臨界時間線與前面討論的一樣(圖中的藍色曲線),它的出現與否和時間間隔T有關.另一種臨界時間線與前面討論的不一樣(圖中的紅色曲線),它在任意T下總是出現.作為1 個例子,給出了T=1.5(對應于圖4(a)中的虛線)時由(9b)式給出的Fisher 零點(圖4(b))和率函數(圖4(c)).類似地,當t較小時的率函數有3 個奇異點①到③,其臨界時間與圖4(a)和圖4(b)中的①到③相對應.

同樣地,圖4(d)給出了T=T7≈1.5210 時的與k的關系(紅色實線).從圖4(d)可以看出,與圖2(d)不一樣的是,當k→0 時,而當k→π 時.根據連續性原理,一定存在一個k?使得=1(如圖4(d)中的k5),因此系統會產生動力學量子相變.這就是圖4(a)中的紅色臨界時間線出現的原因.而且,當T=0 時系統相當于直接由B點一次淬火到D點,此時系統存在動力學量子相變,臨界時間就是圖4(a) 中的紅色實線與T=0的交點.所以紅色臨界時間線與直接從B→D淬火的臨界時間相聯系.另外,從圖4(d)中的紅色實線可以看出還存在兩個臨界動量k3和k4,與3.1.1 節類似,它們對應于藍色的臨界時間線.為了進一步分析這條臨界時間線與第2 次淬火前的臨界時間的關系,給出了 tan2(θ0,k ?θ1,k)/2 與k的關系,結果如圖4(d)中的黑色實線所示.它在虛線處與紅色實線相交于k=k3,這表明圖4(a)中藍色臨界時間線與第2 次淬火前的臨界時間相聯系.

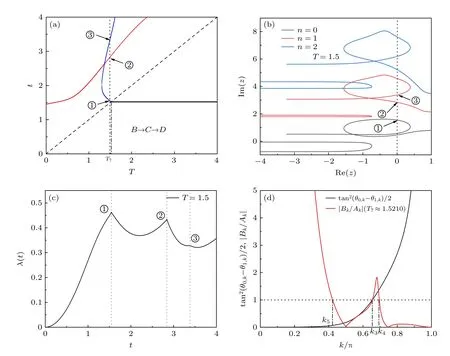
圖4 (a)淬火路徑 B →C →D 對應的臨界時間圖,圖中虛線對應的 時刻為 T =1.5 ;(b) T =1.5 且 t >T 時的Fisher 零點分布;(c) T =1.5 時兩次淬火過程的率函數;(d)黑色實線是 t an2(θ0,k -θ1,k)/2 與k的關系.紅色實線為 | Bk/Ak| 與k的關系,對應的時間間隔為T=T7 ≈1.5210Fig.4.(a) Location of the critical times in the t -T plane for the path B →C →D .The dotted line marks the time for T =1.5 .(b) The Fisher zeros for t >T with T =1.5 .(c) The rate function corresponding to T =1.5 .(d) The black line corresponding to the relationship between t an2(θ0,k -θ1,k)/2 and k.The red line corresponding to the relationship between | Bk/Ak| and k for T=T7 ≈1.5210.

3.2.2 先經過各向異性相變點再經過Ising相變點的兩次淬火

接下來討論先經過各向異性相變點再經過Ising 相變點(D→C →B)的兩次淬火情形.同樣地,圖5(a)給出了T-t平面內的臨界時間.可以看出在第2 次淬火后系統中會出現兩種類型的臨界時間線.一種與前面討論的一樣(圖中的藍色曲線),它的出現與否和時間間隔T有關.另一種臨界時間線(圖中的綠色曲線)在任意T下總是出現,但與3.2.1 節不一樣,它在t=T(對角線上)處與第1 次淬火后的臨界時間線相連.作為1 個例子,給出了T=1.5(對應于圖5(a)中的虛線)時由(9b)式給出的Fisher 零點(圖5(b))和率函數(圖5(c)).當t<2.5 時率函數有5 個奇異點,分別對應于圖5(a)中的①到⑤.其中點③到⑤的臨界時間對應于圖5(b)中n=0的Fisher 零點與虛軸的交點.而點①和②的臨界時間是對應于(9a)式所示的Fisher 零點與虛軸的交點(沒有給出).

同樣地,給出了T=T8≈1.1574 時的與k的關系,結果如圖5(d)中的紅色實線所示.與3.2.1 節類似,當k→0 時→∞k →π,而當 時.所 以也必定有一個k?使得.也就是圖5(d)中的k=k7的臨界動量,它對應的臨界時間線即為圖5(a)中的綠色臨界時間線.顯然這條臨界時間線在T=0 時與直接從D→B淬火的臨界時間相聯系.但是與3.2.1 節不同的是,這條臨界時間線還與第2 次淬火前的臨界時間相交于t=T處.為了進一步說明這種情況,給出了tan2(θ0,k ?θ1,k)/2與k的關系,結果如圖5(d)中的黑色實線所示.從圖5(d)可以看出紅色實線與黑色實線在虛線處相交于k7,這表明圖5(a)中的綠色臨界時間線不僅與直接從D→B淬火的臨界時間相聯系,還與第2 次淬火前的臨界時間相聯系.另外圖5(a)中的藍色臨界時間線與前面討論的類似,這可以從圖5(d)中的藍色實線(對應于T=T9≈1.3879 )與黑色實線在虛線處相交于k6看出.

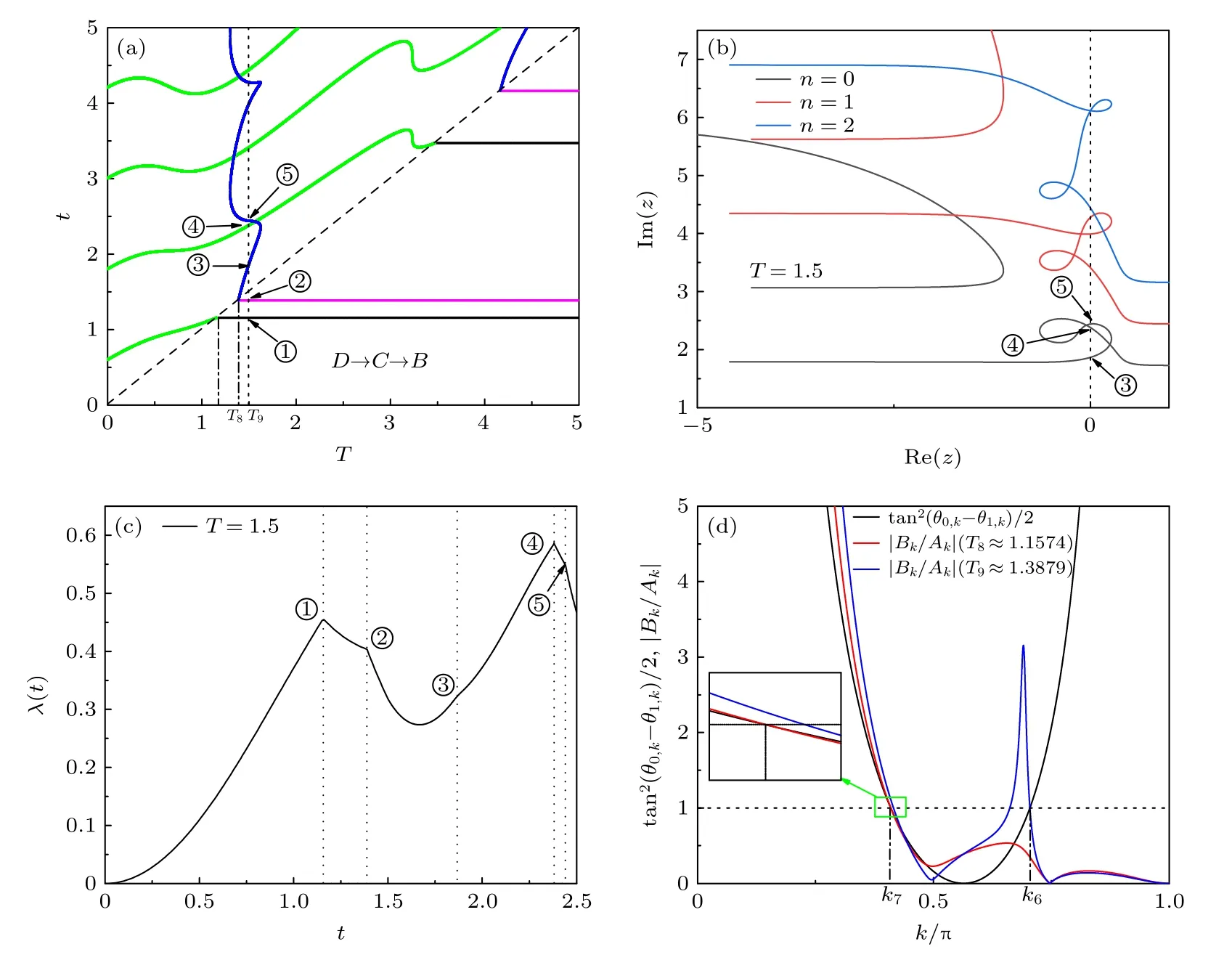
圖5 (a)淬火路徑 D →C →B 對應的臨界時間圖,圖中虛線對應的時刻為 T =1.5 ;(b) T =1.5 且 t >T 時的Fisher 零點分布;(c) T =1.5時兩次淬火過程的率函數;(d)黑色實線是t an2(θ0,k -θ1,k)/2 與k的關系,其中紅色和藍色實線為 | Bk/Ak| 與k的關系,對應的時間間隔分別為 T =T8 ≈1.1574 和T=T9 ≈1.3879Fig.5.(a) Location of the critical times in the t -T plane for the path D →C →B .The dotted line marks the time for T =1.5 .(b) The Fisher zeros for t >T with T =1.5 .(c) The rate function corresponding to T =1.5 .(d) The black line corresponding to the relationship between t an2(θ0,k -θ1,k)/2 and k.The red and blue lines corresponding to the relationships between |Bk/Ak|and k for T =T8 ≈1.1574 and T =T9 ≈1.3879,respectively.

3.2.3 先經過Ising 相變點后同時經過Ising和各向異性相變點的兩次淬火

最后討論先經過Ising 相變點后同時經過Ising 和各向異性相變點(C→B →D)的兩次淬火的情形.圖6(a)給出了T-t平面內的臨界時間.可以看出在第2 次淬火后系統中會出現兩種類型的臨界時間線(紅色和綠色實線).無論T取什么值,這兩種臨界時間線在第2 次淬火后一定存在.作為1 個例子,給出了T=1.5(對應于圖6(a)中的虛線)時由(9b)式給出的Fisher 零點(圖6(b))和率函數(圖6(c)).類似地,圖6(d)中的點①到③分別對應于圖6(a)中的點①到③,而點②和③分別對應于圖6(b)中的點②和③.

同樣地,也給出了tan2(θ0,k ?θ1,k)/2 和(T=T10≈0.9170 時)與k的關系,分別對應于圖6(d)中的黑色和紅色實線.與前面不同的是,當k →0 和k→π 時均有,并且中間某個k時,所以對于任意的T,一定存在兩個k?,使得.其中1 個臨界動量(k8)對應的臨界時間線即為圖6(a)中的綠色臨界時間線.它與圖5(a)中的綠色臨界時間線類似,這同樣可以從圖6(d)中的黑色實線與紅色實線在虛線處相交于k8看出.而另1 個臨界動量(k9)對應的臨界時間線即為圖6(a)中的紅色臨界時間線.它與3.2.2 節中的紅色臨界時間線類似,只與直接從C→D淬火的臨界時間相聯系.

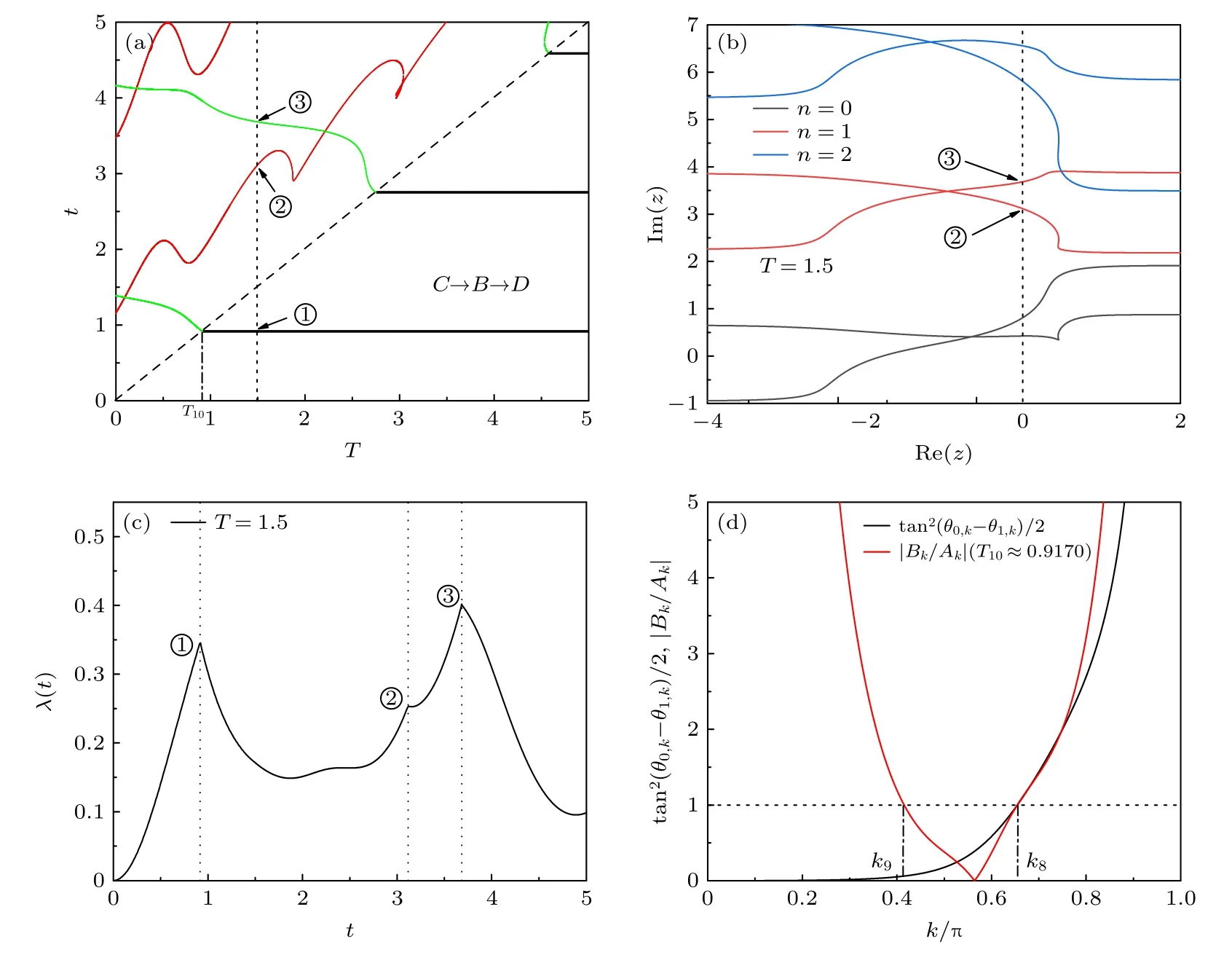
圖6 (a)淬火路徑 C →B →D 對應的臨界時間圖,圖中虛線對應的時刻為 T =1.5 ;(b) T =1.5 且 t >T 時的Fisher 零點分布;(c) T =1.5 時兩次淬火過程的率函數;(d)黑色實線是 tan2(θ0,k -θ1,k)/2 與k的關系,其中紅色實線為 | Bk/Ak| 與k的關系,對應的時間間隔為T=T10 ≈0.9170Fig.6.(a) Location of the critical times in the t -T plane for the path C →B →D .The dotted line marks the time for T =1.5 .(b) The Fisher zeros for t >T with T =1.5 .(c) The rate function corresponding to T =1.5 .(d) The black line corresponding to the relationship between t an2(θ0,k -θ1,k)/2 and k.The red line corresponding to the relationship between | Bk/Ak| and k for T=T10 ≈0.9170.

4 結 論

本文討論了兩次淬火下橫場中XY鏈的動力學量子相變.研究發現,在第2 次淬火后,系統在T-t平面內的臨界時間線有三種典型的情形.情形I:臨界時間只在一定的T范圍內出現,它與第1 次淬火(H0→H1)過程中的臨界時間相聯系,在T-t平面中用藍色曲線表示;情形II:臨界時間在第2次淬火后總是出現,它與從H0直接淬火到H2的過程中的臨界時間相聯系,在T-t平面中用紅色曲線表示;情形III:臨界時間在第2 次淬火后也總是出現,它同時與H0→H1和H0→H2的淬火過程中的臨界時間相聯系,在T-t平面中用綠色曲線表示.

上述三種情形的臨界時間線是否出現,取決于淬火路徑.考慮了兩類典型的淬火路徑,一類是經過同一類量子相變點的兩次淬火,其中包括經過Ising 相變點或者經過各向異性相變點.此時第2次淬火后只有情形I的臨界時間線.另一類是分別經過不同類量子相變點的兩次淬火,其中包括三種情形.第一種是先經過Ising 相變點再經過各向異性相變點,此時第2 次淬火后有情形I 和情形II的臨界時間線.第二種是先經過各向異性相變點再經過Ising 相變點,此時第2 次淬火后有情形I 和情形III的臨界時間線.第三種是先經過Ising相變點再同時經過Ising 和各向異性相變點,此時第2次淬火后有情形II 和一種情形III的臨界時間線.這表明兩次淬火下橫場中XY鏈的動力學量子相變不僅與時間間隔T有關,還與兩次淬火的路徑有關.

除了上述的五種淬火路徑,還有四種其他的淬火路徑.一種是均同時經過Ising 和各向異性相變點的兩次淬火情形,它與均經過Ising 相變點的兩次淬火情形類似.另一種是先同時經過Ising 和各向異性相變點再經過各向異性相變點的兩次淬火情形,它與先經過Ising 相變點再經過各向異性相變點的兩次淬火情形類似.還有一種是先經過各向異性相變點再同時經過Ising 和各向異性相變點的兩次淬火情形,它與先經過各向異性相變點再經過Ising 相變點的兩次淬火情形類似.最后一種是兩次淬火先同時經過Ising 和各向異性相變點再經過Ising 相變點的兩次淬火情形,它與先經過Ising相變點再同時經過Ising 和各向異性相變點的兩次淬火情形類似.