基于時域剪切干涉的納秒脈沖相位測量技術*

潘良澤 劉誠 朱健強

1)(中國科學院上海光學精密機械研究所高功率激光物理聯合實驗室,上海 201800)

2)(中國科學院大學材料與光電研究中心,北京 100049)

提出一種時域剪切干涉技術測量納秒激光脈沖的時間相位分布,該方法將待測脈沖分為彼此之間有數百個皮秒延遲量的兩個脈沖;并在對其中一個脈沖加入適量的頻移后和另一個脈沖合束,得到時域干涉條紋;最后采用相適應的算法,從記錄的時域條紋計算得到納秒激光脈沖的時間相位分布,并進一步計算得到激光脈沖的精細光譜結構.在對測量原理進行系統分析的基礎上,利用數值模擬和實驗對該相位測量技術的可行性進行了驗證,并系統分析了其測量誤差和非理想條件下的各種干擾因素的影響.由于該測量技術不采用任何非線光學方法,可對任何波長的激光脈沖進行測量,具有光路簡單、測量精度高和適用范圍廣等優點,為需要對納秒激光脈沖的時域相位分布進行測量的高功率激光等領域提供了一種簡單便捷的測量新技術.

1 引 言

大能量納秒脈沖激光的脈沖能量可高達萬焦耳量級[1,2],在等離子體發射[3,4]、慣性約束核聚變[5,6]、高能密度物理[7?9]和實驗室天體物理等諸多前沿研究領域都有重要應用.大能量納秒激光脈沖一般是由能量很小的種子脈沖經過結構復雜的激光放大系統產生,在各種復雜非線性物理效應的共同作用下,種子光脈沖的強度和相位分布的微小變化都會對輸出激光脈沖的脈寬和相位產生顯著改變,從而對后續激光物理實驗的實驗精度和對實驗結果的分析造成嚴重影響.為提升裝置的綜合性能和確保實驗結果的準確性,必須要對大能量激光脈沖特性進行精確測量.阿秒到皮秒量級的激光短脈沖的持續時間比光電探測器的響應時間短很多,很難直接測量其時間變化特性,但由于它們一般具有較寬的光譜分布,因此對短脈沖激光的測量一般是在頻譜域進行,即先測量出他們光譜的強度和相位,然后用傅里葉變換來得到其時間分布信息[10?16],常用的此類技術主要包括:頻率分辨光開關法(FROG)[10?12]、光譜相位干涉法[13?15]、雙盲全息測量技術[16].但由于納秒脈沖的光譜寬度一般小于0.1 nm,這些基于光譜測量的技術很難應用于對納秒脈沖的測量,實驗中一般僅能用示波器來記錄其時間強度波形,一直沒有合適的方法來測量其時間相位分布.Fee 等[17]和Gangopadhyay等[18]提出利用光外差法來測量納秒激光脈沖,他們將一束頻率與待測激光脈沖中心頻率有少量偏移的連續光和待測脈沖干涉獲得時域干涉條紋,然后通過帶通濾波的方法獲得納秒脈沖的復振幅分布.在連續光的時間相位被認為是理想平整的情況下,該方法能夠直接獲得納秒脈沖的時間相位分布,但在實際工程應用中,很難得到在能量、波長和相位平整度等方面都與待測量納秒脈沖相匹配的連續光.2011 年,Bowlan 和Trebino[19]提出一種應用于納秒脈沖復振幅的FROG 測量技術,該方法通過使用兩塊標準具分別實現寬延時和精細光譜結構.但是鑒于納秒脈沖的峰值功率密度與皮秒脈沖和飛秒脈沖相比要低得多,在非線性晶體后很難產生較強的相關信號[20],因此該方法僅適用于高功率脈沖,另外,受限于光譜標準具有限的波長分辨率和掃描測量方式,該方法無法應用于脈寬大于十幾納秒的激光脈沖,而且也無法對單脈沖進行測量.

為解決納秒激光脈沖的時間相位測量問題,本文提出一種自參考時域剪切測量技術測量納秒脈沖的時間相位,該方法將待測脈沖分成彼此之間有一定時間延時的兩個脈沖,并在對其中一個脈沖施加一定的移頻后將兩個脈沖合束,得到時域剪切干涉條紋,然后用合適的算法從所記錄到的條紋解調出納秒脈沖的時域相位分布.由于該測量技術不采用任何非線光學方法,可對任何波長的激光脈沖進行測量,而且干涉條紋由待測量光脈沖自身產生,不需要額外的參考光源,因此具有光路簡單、測量精度高和適用范圍廣等優點.本文用數值分析和仿真計算驗證了該測量方法的技術可行性,并分析了移頻量、剪切量、能量對比度和外界噪聲干擾多種因素對測量精度的影響.分析表明,在激光脈沖的持續時間范圍內,當兩束脈沖光的相對延時在0.5%—28%之間,且延時脈沖和移頻脈沖強度比不低于0.1%,信噪比不低于15 dB 時,這種納秒脈沖相位測量技術可以實現高于5%的測量精度,最后通過實驗方法驗證了該測量方法的可行性.

2 基本原理

本文所提的自參考移頻剪切納秒脈沖相位測量技術的基本原理如圖1(a) 所示.待測脈沖E(t)=A(t)exp[iw0t+iφ(t)] ,其中A(t) 為脈沖的時間振幅,w0為脈沖的中心頻率,φ(t) 為脈沖的時間相位.脈沖首先被分成兩束,一束脈沖光通過移頻晶體使得脈沖整體的頻率與原始頻率有一定的偏移,記為E(t)eiδwt,其中 δw代表移頻量大小,另一束不經過移頻晶體,但相對于移頻光束有1 個時間延遲,記為E(t ?τ)=A(t ?τ)exp[iw0(t ?τ)+iφ(t ?τ)],其中A(t ?τ) 表示延時脈沖的時間振幅,φ(t ?τ) 表示延時脈沖的時間相位,τ代表延時大小.兩束光束合束之后經過光電探測器,得到的時域強度場S(t) 可以表示為

其中相位差分布 Δφτ(t)=φ(t)?φ(t ?τ) .

在(1)式的強度表達式中,等式右邊第1 項和第2 項分別代表延時光束和移頻光束的強度分布,第3 項形成頻率為 δw的時間條紋.用示波器記錄下(1)式的時間條紋后,從時間條紋中恢復脈沖相位分布的具體過程如圖1(b)所示,具體數據處理過程如下.

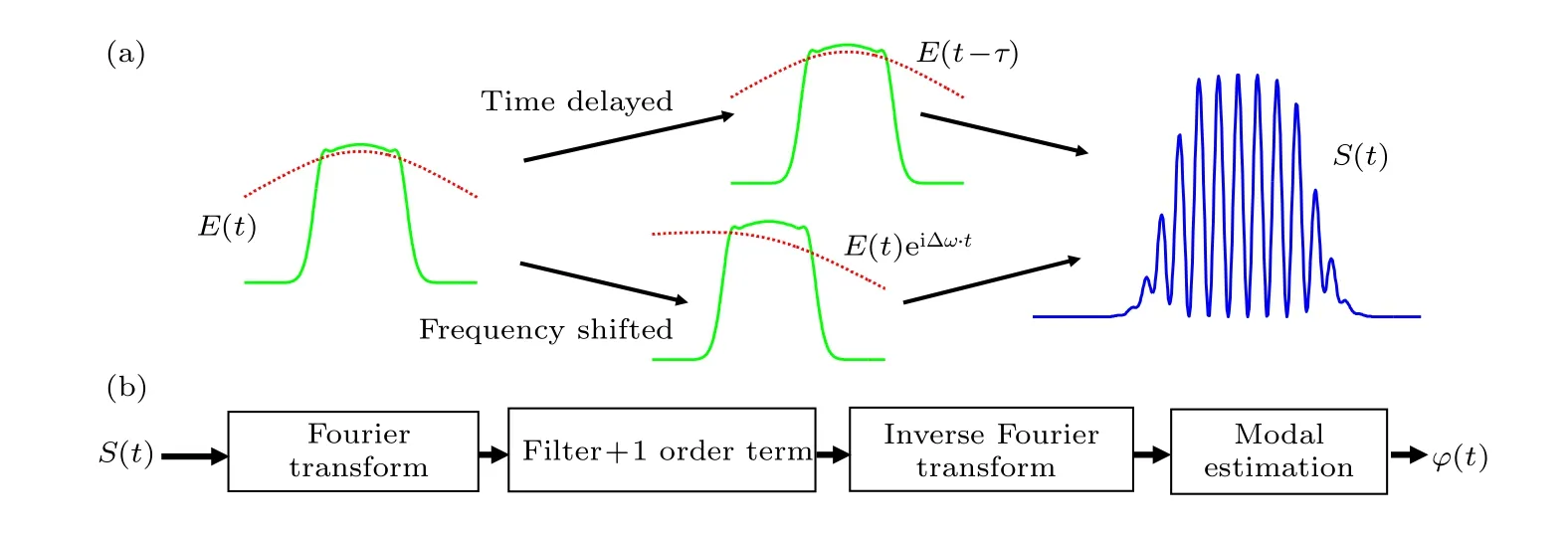
圖1 (a)自參考時域剪切納秒相位測量技術原理;(b)重建過程Fig.1.(a) Schematic diagram of temporal self-referencing technique for the diagnostics of a nanosecond laser pulse;(b) reconstruction procedure.

1) 對記錄到的時域剪切條紋作傅里葉變換得到頻域分布S(w) :

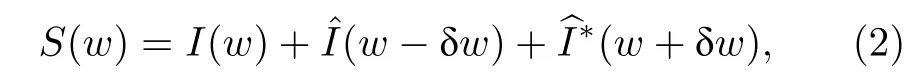
其中I(w)表示零級分量,分別表示±1 級分量.只要選取合適的移頻量就可以使(2)式中各級分量彼此分離,將中心頻率在w=δw的頻譜濾出后平移至坐標中心[21],再作傅里葉逆變換得到,其中忽略了常數相位項取自然對數可以得到

為了定量評價恢復的相位質量,可用(7)式定義的角度來描述恢復脈沖相位分布和實際脈沖相位分布之間的相似度

3 數值驗證

為了滿足采樣定理要求,在本文提出的自參考移頻剪切干涉測量方法中,每個條紋至少要保證有3 個采樣點,移頻量 δw必須小于,其中dt表示由光電探測器與示波器共同決定的采樣分辨率.另一方面,為了使S(w)各級分量之間互不重疊,移頻量δw需要足夠大.若待測量脈沖是1個時間半高全寬為Δt且啁啾率為b的高斯脈沖,S(w)的零級分量在頻率軸上約 4 /ΔtHz的范圍內有意義,一級分量在頻率軸上約 6 /ΔtHz的范圍內有意義,頻移量 δw必須大于.因此,激光脈沖的移頻量大小要介于之間,可確保重建的相位的精準度.

假設待測量脈沖是中心波長為640 nm的單高斯脈沖、隨機啁啾單高斯脈沖、臺階脈沖和雙高斯激光脈沖,它們的時間真實強度波形和時間相位如圖2(e)—(h)所示,其中藍色曲線為真實時間強度,綠色實線為真實相位分布.當所有脈沖的采樣點個數為1024,采樣間隔為dt=125 ps,移頻量大小設為1 GHz,兩脈沖之間的延時設為τ=1.5 ns,兩脈沖強度比為1 時,所得到的時間剪切干涉強度如圖2(a)—(d) 所示.利用前文描述的方法,對圖2(a)—(d)中四組時間剪切干涉條紋進行重建,重建的相位在圖2(e)—(h) 中用紅色虛線表示,可以看出,重建的相位和實際相位差別為千分之一左右,證明了上述方法具有良好的可行性.將所測量的相位和示波器記錄到的相位組合成激光脈沖的時間復振幅,則可以計算出脈沖的精細光譜分布.圖2(i)—(l)中藍色實線表示脈沖的真實光譜,紅色虛線表示測量出的光譜,二者完全符合.

為了檢驗本文所提方法在存在噪聲情況下的測量精度,在時域強度剪切干涉圖上添加了不同程度的噪聲.圖3(a)給出了在圖2(a)—(d)的時域剪切干涉圖上添加不同信噪比噪聲時,重建誤差隨信噪比變化的曲線圖.圖3(b)—(d)的紅色虛線給出了在圖2(b)的時域剪切干涉圖中分別添加10,20,40 dB 信噪比的噪聲時,所得到的重建相位分布,插圖中藍色實線表示根據時域復振幅計算所得的重建光譜分布,紅色虛線表示真實的光譜分布.對比以上的仿真結果可以發現,使用自參考移頻剪切納秒脈沖相位測量技術進行脈沖相位恢復具有很好的抗噪性,對于上述四類脈沖而言,當所記錄時域剪切干涉圖的信噪比不低于15 dB 時,脈沖的相位重建誤差均小于5%,可以認為重建的相位分布與原始的相位分布基本一致.

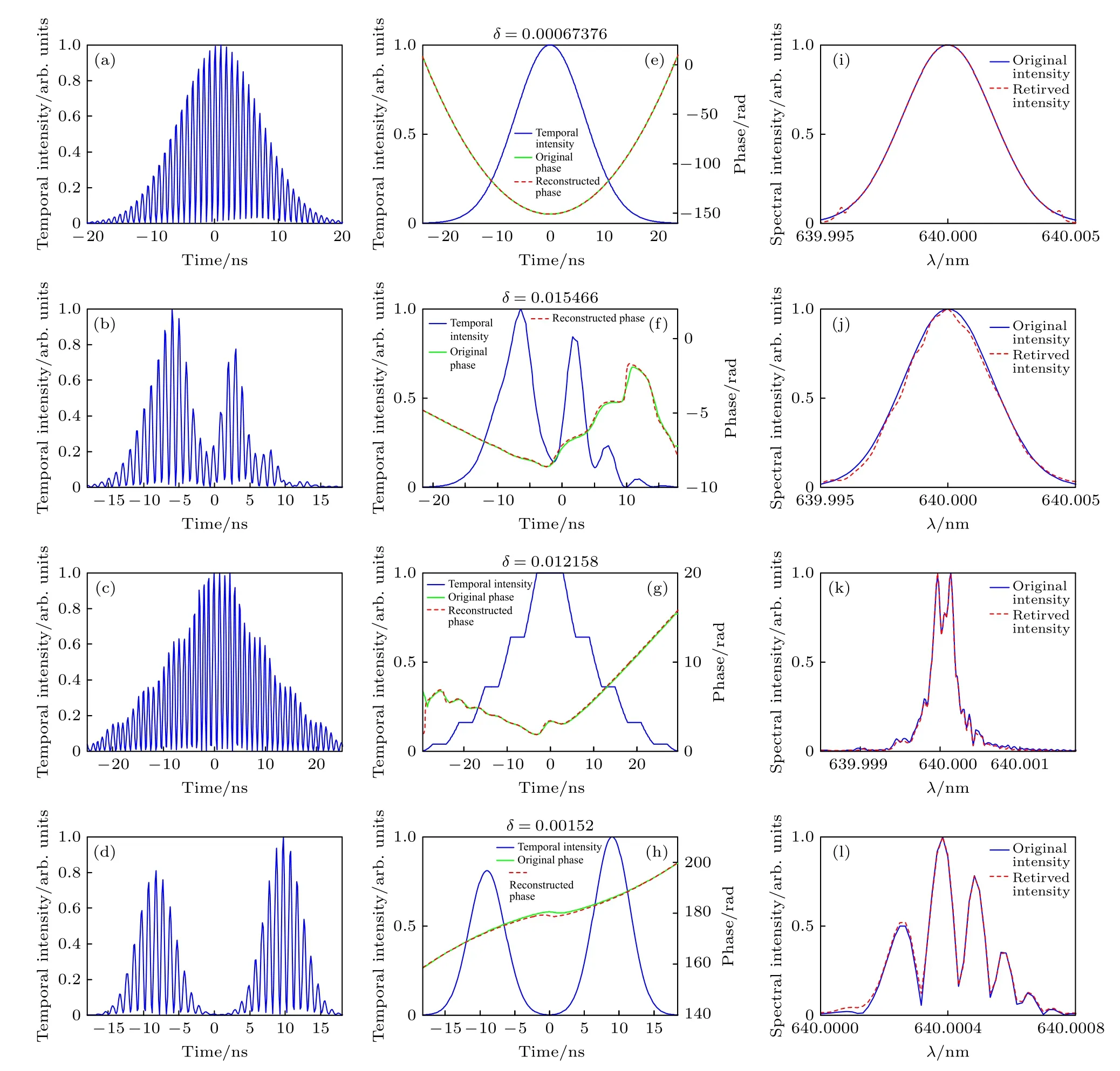
圖2 基于自參考時域剪切的納秒相位測量技術的仿真結果.每列表示不同強度分布脈沖的重建結果,每一列中第一幅圖是合束后的時域剪切干涉圖;第二幅中藍色實線表示脈沖的時間強度分布,綠色實線為原相位分布,紅色虛線為重建的相位分布;第三幅中藍色實線為計算所得的光譜分布,紅色虛線為原光譜分布Fig.2.Simulation results of phase retrieval of nanosecond laser pulses based on temporal shearing interferometry.Each column represents reconstructed results.In each column,the first plot represents the recorded temporal interferogram;the second plot presents the original temporal intensity distribution(blue solid line),original temporal phase distribution(green solid line) and reconstructed temporal phase distribution(red dashed line);the third shows the original spectral intensity distribution(blue solid line) versus reconstructed spectral intensity distribution(red dashed line).

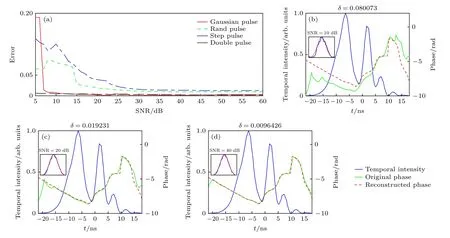
圖3 (a)不同強度分布的脈沖,相位重建誤差隨信噪比變化的曲線圖;(b)—(d)在圖2(b) 所示的移頻剪切圖中分別添加信噪比(SNR)為10,20,40 dB的噪聲下的重建結果,其中的插圖表示計算得到的光譜強度分布Fig.3.(a) Reconstructed error between reconstructed and original signals as a function of the SNR for pulse with different intensity distribution;(b)–(d) reconstructed pulse distribution for SNR of 10,20,40 dB,respectively,and the computed spectra is presented in the inset.

在上面的計算中,脈沖之間的延時量(這里相對延時定義為τ/Δt,其中τ為延時量大小,Δt為待測脈沖的時間半高全寬)太大會使得所求的相位梯度存在高階微分項,太小則會導致求得的相位梯度被噪聲覆蓋,因此脈沖相對延時量大小也是影響重建相位精度的重要因素.圖4(a)為圖2(e)—(g)所示的3 類不同脈沖的相位重建誤差隨著相對延時變化的曲線圖(延時脈沖和移頻脈沖的相對強度設為1,移頻量大小設為1 GHz,信噪比設為30 dB).可以發現,在脈沖的相干時間范圍內,當兩脈沖的相對延時在0.5%—28%之間時,該相位恢復算法能夠可靠地恢復出待測脈沖的時域相位分布.

延時脈沖和移頻脈沖之間的相對強度相差過多時,會導致時域剪切干涉條紋被原脈沖強度所覆蓋,影響最終相位重建精度,為探究脈沖相對強度對測量結果的影響,在脈沖之間的相對延時為15%,頻移量 δw為1 GHz,信噪比為30 dB的情況下,圖4(b)給出了圖2(e)—(h)所示4 類不同脈沖重建誤差隨著相對強度變化的曲線圖.從誤差曲線可以發現,當兩脈沖之間的強度比在不低于0.1%時,該方法均能夠重構出待測納秒脈沖可靠的時域相位分布.

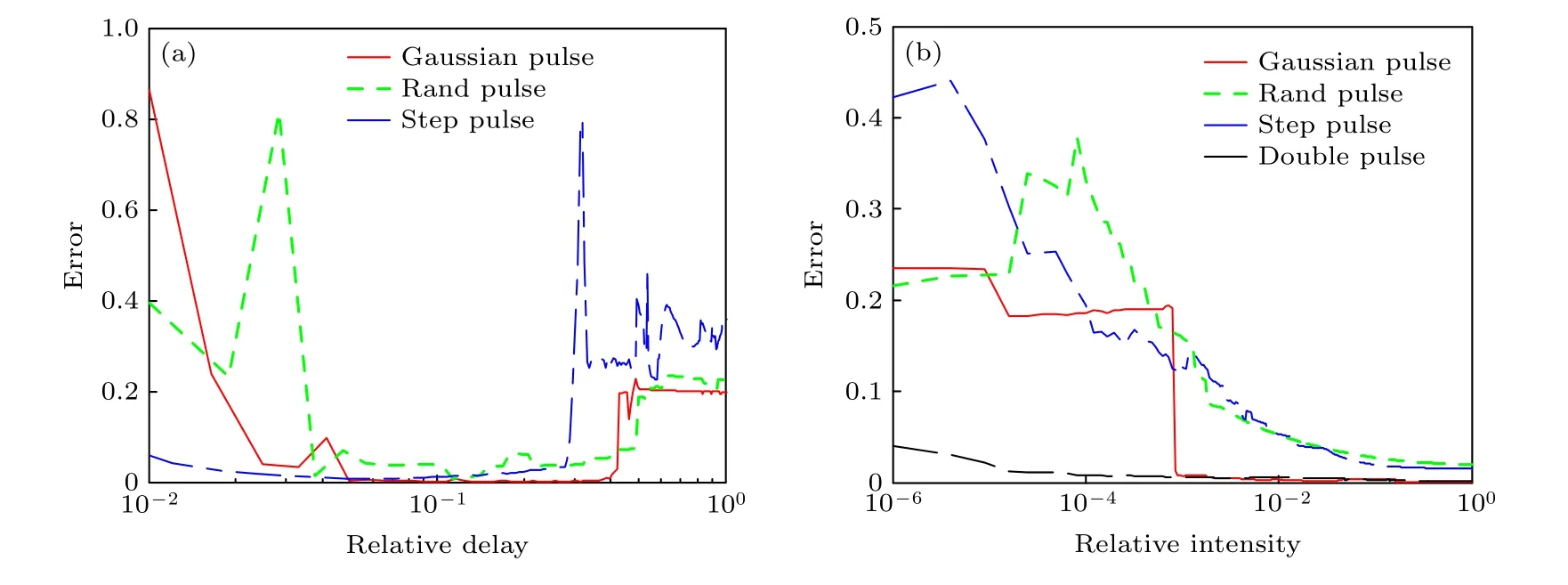
圖4 (a) 不同強度分布的脈沖,相位重建誤差隨相對延時變化的曲線圖;(b) 不同強度分布的脈沖,相位重建誤差隨相對強度變化的曲線圖Fig.4.(a) Reconstructed error between reconstructed and original signals as a function of relative delay for pulse with different intensity distribution;(b) reconstructed error between reconstructed and original signals as a function of relative intensity delay for pulse with different intensity distribution.

4 實驗驗證

實驗使用的光源是1 個中心波長在640 nm的納秒脈沖激光器,來驗證該納秒脈沖相位測量技術的可行性.該激光器可提供重復頻率1—10 MHz,最高峰值功率在50 mW,脈寬為20 ns的納秒激光脈沖,聲光移頻晶體的型號為KG-1500-640-0.1-PB,可以提供1—2 GHz的移頻量大小,待測激光脈沖在經過聲光晶體之后對待測脈沖產生一定的移頻量.最后通過1 個帶寬為2.5 GHz,型號為PDA2.5GA3KSFA的光電探測器和1 臺最大采樣率為20 GS/s,型號為Lecroy WaveRunner 620Zi的示波器來記錄最后的剪切干涉條紋.通過調節光學延時線中的平移臺,使得實驗中延時脈沖和移頻脈沖的延時量τ=200 ps .在實驗中,移頻量的大小設為1.16 GHz,光電探測器記錄到的時間剪切干涉圖由2048 個采樣點組成,采樣間隔是50 ps,光電探測器記錄到的時間剪切干涉條紋如圖5(a)所示.圖5(b)所示是重建得到的待測激光脈沖的時間相位分布(紅色虛線)以及由示波器記錄到的待測激光脈沖的時間強度分布(綠色實線).對待測激光脈沖的時間復振幅分布|A(t)|exp[iφ(t)] 作傅里葉變換可以得到待測激光脈沖在光譜域的復振幅分布,各發脈沖的光譜強度計算結果如圖5(c)中紅色虛線所示.為了進一步提升本文所提方法的可信度,這里使用掃描式的法布里珀羅干涉儀(Thorlab SA210-5B)來測量不同輸出脈寬情況下激光器的輸出光譜,結果如圖5(c)中藍色實線所示.可以發現,掃描式的法布里珀羅干涉儀測得的光譜結構與前文計算得到的光譜結構基本重合.進一步說明了本測量方法的可靠性.

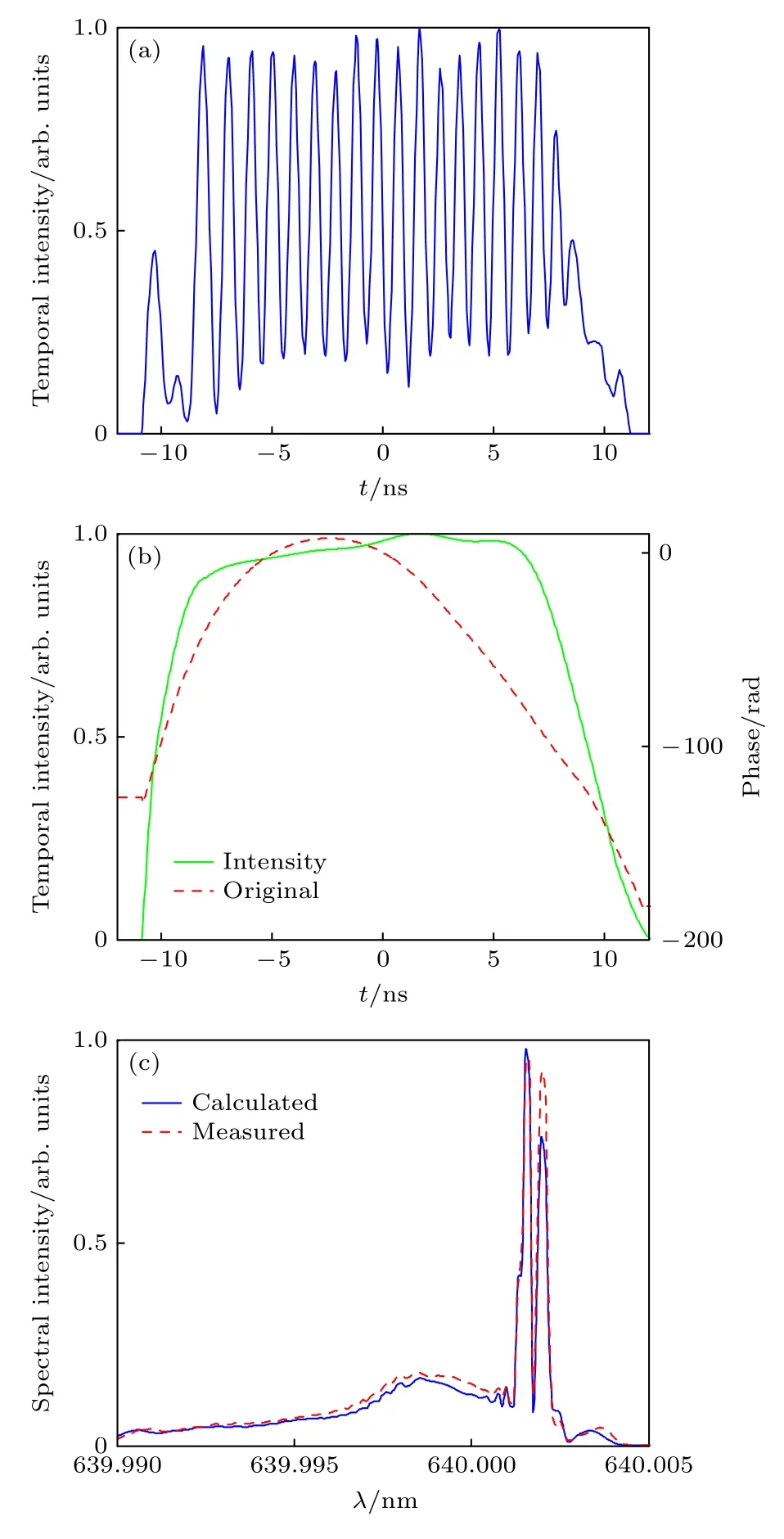
圖5 實驗結果 (a) 實驗記錄的時間剪切干涉圖;(b) 重建的時間相位分布(紅色虛線)和示波器記錄到的時間強度圖(綠色實線);(c) 計算光譜強度分布(藍色實線)和測得的光譜強度分布(紅色虛線)Fig.5.Experimental result:(a) Recorded temporal shearing interferogram;(b) reconstructed temporal phase distribution(red dashed line) and the temporal intensity distribution(green solid line) recorded by oscilloscope;(c) calculated(blue solid line) and measured(red dashed line) spectral intensity distribution.

5 結 論

本文提出了一種自參考方法來測量納秒脈沖的時域相位分布和精細光譜結構.該方法通過將待測脈沖分為兩束有一定時間延時的脈沖對,對其中一束脈沖經過移頻調制后重新合束來實現時域剪切干涉.利用示波器記錄所形成的時域干涉條紋,通過解調算法解調時域剪切條紋可以得到待測納秒脈沖的相位梯度,再通過模式估計方法得到納秒脈沖的時域相位分布.通過仿真實驗驗證了該方法測量納秒相位的可行性,并研究了關鍵參量對恢復相位分布質量的影響.仿真結果表明:在脈沖的相干時間范圍內,脈沖對之間的相對延時介于0.5%—28%之間,強度比不低于0.1%,記錄的時域剪切圖的信噪比不低于15 dB,通過選取合適的移頻量大小,使用本方法對不同強度分布的納秒脈沖進行相位恢復均能夠取得較好的恢復結果.最后通過實驗驗證了該測量方法的可行性.本方法不需要任何參考光,沒有利用光的非線性效應和迭代算法,只需要使用常規的移頻器和示波器,并通過簡單的計算,就可以獲得納秒脈沖的時域相位分布和精細的光譜結構.因此,該方法具有光路簡單、探測靈敏度高、實時探測、測量精度高等優點,可以廣泛應用于各類納秒脈沖甚至微秒脈沖的相位測量中.