Y3Fe5O12-CoFeB 自旋波定向耦合器中的自旋波*

閆健 任志偉 鐘智勇

(電子科技大學,電子薄膜與集成器件國家重點實驗室,成都 610054)

介紹了一種基于Y3Fe5O12 和CoFeB 復合結構耦合的新型定向耦合器,并利用微磁學仿真軟件Mumax3及其配套工具鏈分析了自旋波在其中的傳播特性.通過在Y3Fe5O12 定向耦合器中添加一種高飽和磁化強度材料(CoFeB)來增強耦合波導的耦合效率,并從器件的尺寸形狀、內部等效場以及耦合機理等角度分析了其變化原因.結果表明,相較于傳統的定向耦合器,這種復合結構能夠極大地降低自旋波在耦合波導間的耦合長度.從應用的角度看,在功能相同的情況下,整個器件的長度可以縮短數倍,具有更好的發展前景.

1 引 言

目前的主流計算系統依賴電荷來執行運算功能,該框架中的基本電路元器件是晶體管[1,2],但是伴隨著器件不斷小型化[3,4],一方面集成電路受到物理極限等問題的制約而難以取得突破性進展[5],另一方面,隨著機器學習以及神經網絡計算的研究愈發深入,晶體管所提供的布爾運算也顯得捉襟見肘[6,7].從長遠發展的角度看,新型的信息處理器件的誕生已成為一個必然的趨勢[8?10],而自旋波器件在高速、低功耗、非布爾運算等領域展現的獨特優勢讓其成為了眾多新型器件的“突出者”[11],受到了廣大研究者的青睞,其中自旋波耦合器作為自旋波器件間的連接單元成為了研究熱點[12?15].Sun 和Vittoria[16]研究了自旋波在雙層無限大薄膜間的耦合情況,奠定了自旋波定向耦合器的產生以及后續發展.隨后Friedrich 等[17]提出了一種基于三維結構的定向耦合器設計,從而加大了器件的靈敏度.2015 年到2017 年,Sadovnikov 等[18?21]提出側邊耦合結構,并實驗證實了兩個耦合波導之間的耦合效率與磁化方向、形狀和大小以及外部環境有關,因此整個器件的參數選擇需要權衡各個結構的尺寸形狀以及材料的磁性參數.近些年可重構自旋波定向耦合器的提出也讓器件的使用更加靈活[22,23],能夠在不改變結構參數的情況下只通過外加的激勵條件改變定向耦合器的輸出,從而為邏輯計算提供了新的方法.

雖然目前所提出的納米級自旋波定向耦合器的設計在非自旋波傳播方向的兩個維度上達到了納米級別的尺寸,但在傳播方向上實現一個簡單能量轉換的功能都需要數微米,這樣的尺寸設計過于龐大以至于無法大規模集成[24,25].因此,對自旋波定向耦合器的耦合效率的研究尤為重要,這直接決定了器件的大小在同類型的器件中是否具有競爭力.基于傳統單種材料定向耦合器,本文提出了一種Y3Fe5O12(YIG,釔鐵石榴石鐵氧體)與CoFeB 耦合型自旋波定向耦合器的模型,通過增大自旋波的耦合效率來縮短器件的尺寸.通過分析磁性結構內部有效場的分布探討CoFeB 給YIG 波導帶來的變化,研究偶極耦合作用和交換耦合作用在自旋波傳播過程中的比重,并對整個器件尺寸進行分析,對耦合器在實際中的應用做出一般性的考量.這些結果對自旋波器件的發展以及實用性的探索具有一定意義.

2 模型建立

基于YIG-CoFeB的耦合型自旋波定向耦合器如圖1 所示,該耦合器采用了雙波導側邊耦合模式,其兩條寬度為100 nm,厚度為30 nm的自旋波波導(S1 和S2)平行放置,間隙寬度為30 nm,上方的波導比下方的波導稍微長一些用來進行自旋波的注入,微波天線放置在上方波導的最左側位置,使用目前已知的阻尼最小的磁性材料YIG 作為自旋波的傳播波導材料,以減小自旋波在整個結構中因傳播而發生的幅值損耗.為了比較間隙層參數的影響,研究了間隙層中添加CoFeB 和不添加任何材料作為對比.需要注意的是,盡管由于耦合作用會使CoFeB 中磁矩發生偏轉,但由于YIG的飽和磁化強度遠小于CoFeB的飽和磁化強度,所以CoFeB 中的偏轉強度遠小于YIG 中的值,故自旋波在CoFeB 中的耦合可以忽略.整個結構沿+x方向磁化,一旦磁化狀態穩定,由于x方向上的尺寸遠大于其他兩個方向上的尺寸,形狀各向異性會使得磁矩朝向一致,故無需添加外磁場.

圖1 YIG-CoFeB 自旋波定向耦合器結構示意圖Fig.1.Schematic diagram of the structure of YIG-CoFeB spin wave directional coupler.

微波天線上施加小幅度正弦磁場用來產生局部微擾,使用Landau-Lifshitz-Gilbert(LLG)方程來描述結構內部磁矩的動態變化,其具體形式如下:

其中,M為磁化強度,Ms為飽和磁化強度,Heff為內部有效場,α為材料阻尼因子.該方程描述的是磁矩在有效場Heff作用下的進動過程,因此求解該方程的核心即為有效場分布的求解.利用微磁學仿真軟件Mumax3進行數值模擬計算時,有效場的貢獻來源主要是偶極作用產生的偶極能以及交換作用產生的交換能.

整個模型的參數如下所示:YIG[26]的飽和磁化強度Ms=140 kA/m ,交換常數Aex=3.5×10?12J/m ,阻尼系數α=0.0002;CoFeB[27]的Ms=1150 kA/m ,Aex=16×10?12J/m,α=0.005.根據交換長度公式Lex=可得YIG波導的交換長度約為16.85 nm,因此將網格大小設置為10 nm × 10 nm × 10 nm 可滿足自旋波傳播要求,對于尺寸精度更細微的結構可以對網格結構再進行調整.微帶天線的寬度為20 nm,放置在整個結構的左側,可提供幅度為1 mT、頻率值為2.88 GHz的正弦磁場用以向結構中注入自旋波.此外,將波導的最后50 nm的阻尼常數設置為0.5,用來減少自旋波在端口處的反射.

3 YIG-CoFeB 定向耦合器中自旋波傳播及色散關系

下面利用色散曲線表征定向耦合器的工作狀態.為了得到合理的數據,需要在微波天線中施加sinc 場,其形式為

微波場的方向為y方向,幅值h0=0.001 mT,截止頻率fc=20 GHz,t0=50 ps.圖2(a)為該sinc場在頻域下的曲線圖,在sinc 場的作用下可以產生0—10 GHz的等幅磁場,可以作為色散曲線的激勵場.通過計算得到YIG 單波導的色散關系如圖2(b)所示,這是該種結構下的最低寬度模式的自旋波的色散曲線.

圖2 (a) 色散曲線求解中激勵場在頻域下的顯示;(b) 孤立YIG 波導中的色散曲線Fig.2.(a) Display of the excitation field in the frequency domain in the solution of the dispersion curve;(b) dispersion curve of isolated YIG waveguide.

之后仿真模擬并計算了間隙為Air(YIG/Air/YIG 結構)和CoFeB(YIG/CoFeB/YIG 結構)的雙YIG 波導的色散曲線,如圖3 所示,可以發現色散曲線發生了劈裂,由原先的最低寬度模式分裂為兩種集體模式:對稱模式和反對稱模式(對應S 和AS,參見圖3(a)),從而使得兩種自旋波模式在每個單個波導中同時被激發,在同一頻率的激勵下具有不同的波數,因此自旋波能量在兩個波導之間周期性地傳輸和分配.圖3 和圖3(b)分別表示在間隙層中填充有空氣和CoFeB的定向耦合器中的自旋波色散關系,可以很清楚地看到在CoFeB 填充結構下S 態和AS 態的間隔要大得多.在2.5—5 GHz 下的自旋波可以有效地進行傳播,為了便于觀察出兩種結構下自旋波耦合長度的變化,在2.88 GHz的頻點上激勵自旋波(圖3(a)和圖3(b)中紅線處的 Δk1和 Δk2代表兩種情況下的波數差),可以清楚地看到后者比前者大,約為前者的4 倍.

圖3 間隙處分別填充(a) Air 和(b) CoFeB 情況下的自旋波色散圖Fig.3.Spin wave dispersion curve when the gap is filled with(a) Air and(b) CoFeB.

將自旋波的能量從一個波導完全傳播到另一個波導所需的距離定義為耦合長度,其值如下:

其中ks和kas分別表示相同頻率下S 態和AS 態模式下自旋波的波數.根據(3)式,添加CoFeB 后結構的耦合長度會減小到1/4,這是一個相對較大的值,意味著在執行相同功能的前提下尺寸減少了3/4.

自旋波在每個波導中的傳播方向上的能量可以表示為

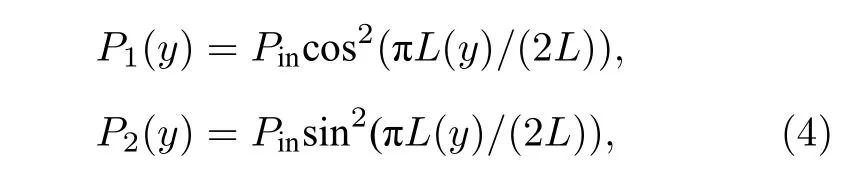
其中,P1為波導S1 中左側的輸入能量,L(y) 是指耦合的波導之間相互作用的長度.從圖4(a)可以看出,在填充CoFeB的耦合結構中,能量完全轉換要大約500 nm的距離,而這個值在填充空氣的結構中是2000 nm 左右.此外,為了更直觀地說明這一情況,通過微帶天線激勵了2.88 GHz 下的自旋波(圖4(b)).紅色和藍色像素代表自旋波的幅度,顏色越深,幅度就越強,這反映了兩種結構下能量的耦合過程.其中的L1和L2分別表示間隙為Air 以及CoFeB的定向耦合器下的耦合長度,可以很直觀地觀察到,L1≈4L2.因此,耦合長度對于自旋波器件的設計來說是一個關鍵參數,它影響著整個器件的大小以及最高使用頻率限制.

圖4 (a) 定向耦合器的輸出隨著波導長度變化的關系圖;(b) 2.88 GHz 下間隙處填充Air 和CoFeB的定向耦合器工作過程中自旋波傳播彩圖Fig.4.(a) Relationship between the output of the directional coupler and the length of the waveguide;(b) color image of spin wave propagation during operation of the directional coupler filled with Air and CoFeB in the gap at 2.88 GHz.

4 內部等效場及參數分析

從圖4(b)可以發現,除了耦合長度的改變之外,自旋波在y軸方向上的振幅也發生了改變,在間隙為空氣的定向耦合器中,自旋波在寬度方向上振幅幾乎不發生變化,而在間隙為CoFeB的結構中,寬度方向上的自旋波振幅發生了明顯的衰減,越靠近CoFeB的地方,自旋波的振幅越低.為了解釋這一現象,繪制了兩種不同定向耦合器的內部有效場分布,如圖5 所示,橙色數據線表示YIG/Air/YIG 結構,藍色線代表YIG/CoFeB/YIG 結構.從圖5 可以發現,中心區域有效場要大得多,這是由于CoFeB[1]的飽和磁化強度較高(幾乎是YIG[2]的8 倍),波導區域離CoFeB 區域越近,有效場也越大,這使得在YIG 波導上對稱的內部場分布變成非對稱狀態.在不考慮各向異性能、塞曼能、熱能和少量貢獻能的情況下,整個系統的能量可分為偶極相互作用能和交換相互作用能.圖5插圖給出了兩種結構下的能量大小,通過添加CoFeB,發現能量增加了數十倍,這意味著交換和偶極相互作用大大增強.因此,可以認為自旋波在兩個耦合的條帶上轉換更為頻繁.

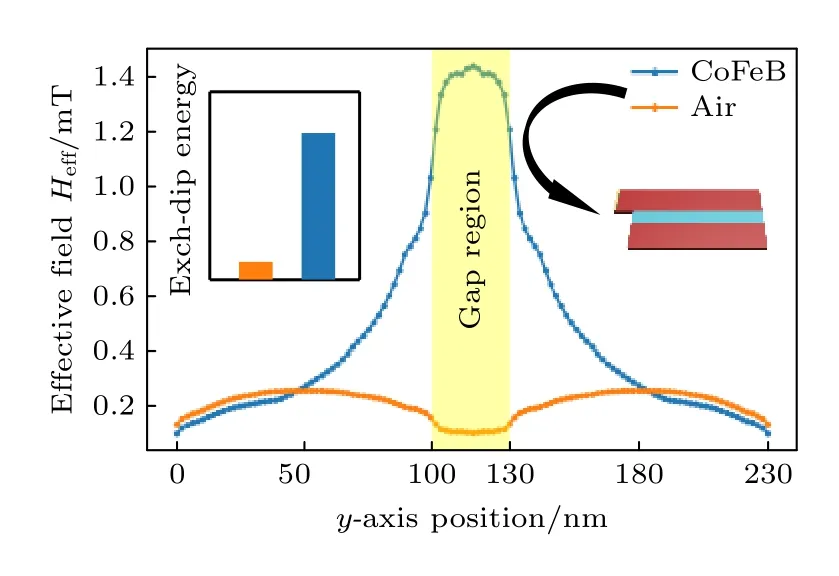
圖5 間隙處填充Air 和CoFeB的定向耦合器中內部有效場分布Fig.5.Internal effective field distribution in the directional coupler filled with Air and CoFeB at the gap.

為了表征交換耦合和偶極耦合在YIG-CoFeB定向耦合器中的作用情況,可以通過改變CoFeB層的寬度來作仿真對比.根據之前的介紹,YIG 波導的交換長度約為16.85 nm,當結構間距離大于這個值時,交換耦合作用幾乎可以忽略,假定此時只有偶極耦合作用.圖6(a)是間隙層寬度為30,40,50 nm 時,不同CoFeB 寬度下的耦合長度值,CoFeB 被放置在兩條波導的中心,間隙層中未填充CoFeB的區域為空氣.當CoFeB的寬度較小時,其與YIG 波導間的間隔較遠,這時耦合作用主要由偶極耦合作用主導,在這種情況下,隨著CoFeB 寬度的增加,耦合長度相對線性地減少.隨著CoFeB 寬度進一步增加,YIG 和CoFeB 間的交換耦合作用逐漸增強,這時耦合作用包括偶極耦合和交換耦合,從圖6(a)可以發現,當CoFeB 快要填充滿間隙層時,曲線的斜率變大(黑色圓形框).圖6(b)給出了間隙層寬度為100 nm 時,不同CoFeB 寬度下YIG 波導S1,CoFeB 間隙層以及YIG 波導S2 間的耦合能量值,從圖6(b)可以發現,當CoFeB的寬度較小時,交換能值較小,系統的總能量主要由偶極能提供,但當CoFeB 寬度較大時,交換能也隨之增大,并且當CoFeB 填充滿間隙層時曲線斜率變大(黑色方框),與耦合長度的關系相對應.因此,可以說明交換作用和偶極作用效果一致,都會使得耦合長度減小,但是主要的貢獻來源還是后者.

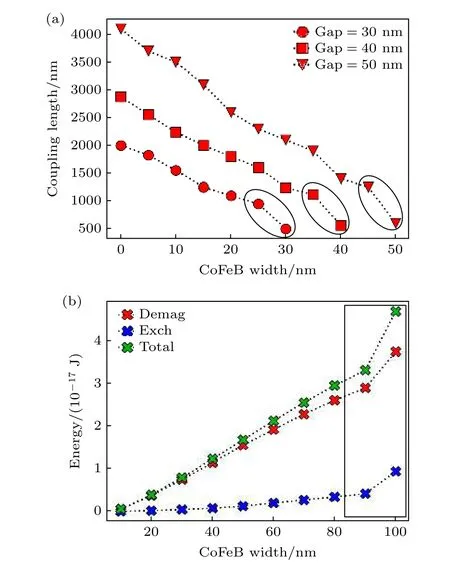
圖6 (a) 耦合長度隨CoFeB 寬度的變化;(b) 不同CoFeB寬度下器件的內部能量值Fig.6.(a) Coupling length varies with the width of CoFeB;(b) the internal energy value of the device under different CoFeB widths.

圖7 呈現了耦合長度L與波導幾何參數的關系.通過分析圖7 可以總結出減小耦合長度的方式:減小波導寬度、增大波導厚度、減小間隙寬度、增大外磁場強度(x方向).這些方式來源于波導內部的耦合作用以及波導間耦合作用的競爭.一般來說,當波導內部的耦合強度遠大于波導間的耦合強度時,才會導致自旋波在兩條波導上傳播需要一定的距離,但是當波導間的耦合作用增強時,則會減小這個距離,通過分析仿真數據得到1 個唯象公式來反映波導中耦合長度與耦合強度的關系:

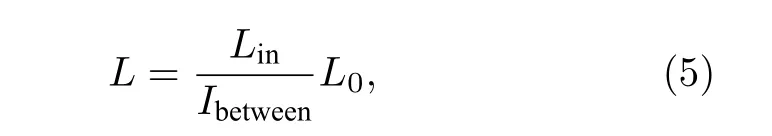
其中,Lin為波導內部自旋波耦合作用強度,Ibetween為波導間耦合作用強度,L0為一般性耦合長度(只在形式上有意義,主要與波導的材料有關).通過(5)式能夠發現,可以通過改變Lin和Ibetween來改變耦合長度,雖然上述的情況都會使得耦合長度發生改變,但作用機理卻不同.圖7(a)所示的減小YIG的波導寬度主要是增大波導內的耦合作用,而波導間的耦合作用幾乎不發生改變,所以耦合長度減小;圖7(c)所示的改變間隙寬度主要是增大波導內的耦合作用,而每個波導內部的耦合作用幾乎不發生改變,所以耦合長度減小;圖7(b)所示的增大結構厚度既增大波導內的耦合作用,又增大波導間的耦合作用,但當厚度增加到一定程度時(本結構中為30 nm 左右),兩種耦合作用的增大趨于飽和,則耦合長度也會趨于飽和;而圖7(d)所示有效場的增加導致自旋波波數的減小,也會使得波導內部的耦合強度減小.

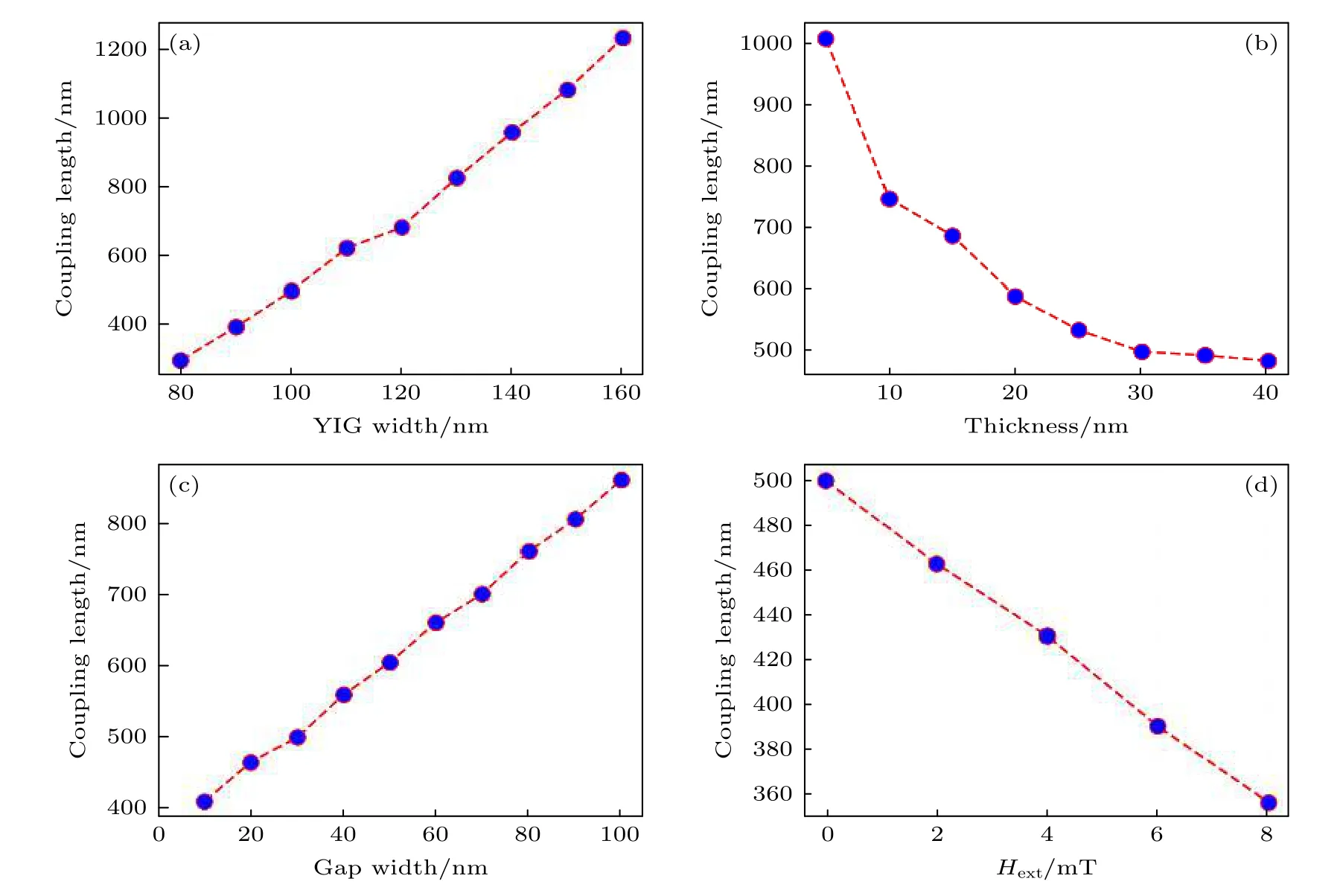
圖7 耦合長度隨著(a) YIG 波導寬度、(b) 波導厚度、(c) 間隙寬度和(d) 外磁場的變化Fig.7.Coupling length varies with(a) YIG waveguide width,(b) waveguide thickness,(c) gap width,and(d) external magnetic field.

出于器件在實際應用中的考慮,需要計算不同頻率下定向耦合器的耦合長度,因為一旦確定了材料尺寸參數和自旋波類型,相應的功能特性也就固定了,然后可以根據所需功能簡單地選擇參數.對于本結構下最低階模式的自旋波激勵,可從頻率2.5 GHz 至4.5 GHz的范圍內觀察到相對明顯的模式分離,而不會受到高階模式的干擾.圖8 中,紅線表示YIG/Air/ YIG 結構,藍線表示YIG/CoFeB/YIG 結構,可以看出定向耦合器的耦合長度隨著頻率的增加而增加.通過用CoFeB 層代替空氣層,線性的變化也增加了,因此該結構具備了更好的調控性.

圖8 不同頻率下定向耦合器的耦合長度Fig.8.Coupling length of directional coupler at different frequencies.

5 結 論

通過上述微磁學的仿真結果以及數據分析,發現定向耦合器的間隙是影響其工作效率的一個主要因素.基于YIG 自旋波定向耦合器結構,本文提出了一種YIG-CoFeB的復合耦合型結構,在該結構中,自旋波在兩條耦合波導上的耦合效率得到了極大的提高,耦合長度降低,由原來的2000 nm 降低為500 nm,因此在實現同樣功能的前提下,整個器件的尺寸會減小數倍.本文還通過數值模擬揭示了該種耦合效率提高的機制,發現CoFeB的存在使磁性結構內部有效場增大,直接導致了自旋波在其中色散關系的變化,進一步研究發現偶極耦合作用的提高是耦合效率提升的根本性原因.最后研究了整個結構的尺寸參數和自旋波頻率的影響,為器件在實際應用中參數的考量奠定了基礎.所有的這些結果為自旋波定向耦合器的發展和應用提供了重要的思路和方法.