基于主波峰的自適應波形重跟蹤算法研究

莫德麗 趙銀軍, 陳國清 梁 珊 童 凱 梁玉蓮,

1 南寧師范大學地理科學與規劃學院，南寧市明秀東路175號，530001 2 南寧師范大學北部灣環境演變與資源利用教育部重點實驗室,南寧市明秀東路175號，530001 3 南寧師范大學廣西地表過程與智能模擬重點實驗室，南寧市明秀東路175號，530001

衛星測高技術起初是為研究海洋環境所研制的，在全球海平面、冰川監測等領域得到了廣泛應用。近年來，眾多學者逐漸將其應用于內陸水體水位變化監測[1-5]，但對于地形復雜且水面寬度不大的河流來說，衛星測高的精度有待提升。主要提升方法包括：1)對各種改正參數進行優化，如電離層延遲校正、對流層干濕分量改正及地球物理項改正；2)通過波形重跟蹤算法提高衛星至河流表面距離的觀測精度。很多學者針對近海海域及內陸湖泊的水位監測進行了算法改進，例如基于子波形的波形重跟蹤算法[6]、基于主波峰的波形重跟蹤算法[7]、多子波多權重閾值重跟蹤算法[8]等，但在應用于河流水位監測時的精度還有進一步提升的空間。

尋找主波峰是波形重跟蹤算法中的關鍵和難點(圖1)。由于受陸地反射效應引起的衛星測高回波波形的污染，衛星測高精度均受限于湖泊及河流區域。但相比湖泊水位觀測，河流水體反射的回波波形更為復雜，在尋找主波峰時更易受噪聲影響。其次，同一衛星軌道在不同時期的回波波形復雜多變，以一種算法難以適應整個水位監測時期的精度。為此，本文針對河流水體，在基于主波峰波形重跟蹤算法[7]的基礎上提出一種基于主波峰波形的自適應重跟蹤算法(AMWRT)，并以長江中游河段為研究區，利用水文站日平均實測水位數據對其進行精度檢驗。

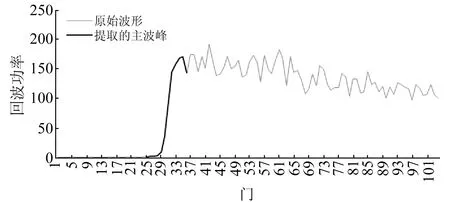
圖1 主波峰提取示意圖

1 研究區概況與數據源

1.1 研究區概況

長江中游位于湖北省中南部(111°45′～114°16′E，29°26′～31°10′N)，流經宜昌市至湖口縣，全長955 km，流域面積約68萬km2，洞庭湖水系(四水流域)、漢江分別位于長江中游的南北兩岸。長江經過的湖北省西部地區兩側多為高山，流水容易匯集，加上河道彎曲，導致洪水宣泄不暢，極易潰堤成災[9]。因此，精準監測長江中游水位變化，對于防汛抗旱、調蓄能力評估等具有重要的指導意義。本文研究區選擇長江中游的枝城水文站附近河道(圖2)，沿坡兩岸地理環境較為復雜，分布有植被及建筑物等。

圖2 研究區位置

1.2 數據來源

Jason-2衛星波形地球物理數據(SGDR)來源于法國國家空間研究中心的衛星海洋學存檔數據中心(https:∥www.aviso.altimetry.fr/en/home.html)，時間范圍選取2008-07～2016-07(cycle001～cycle302)。SGDR數據包含20 Hz的波形數據、衛星地面距離數據和一些質量控制字段及地球物理校正數據。Jason-2衛星每運行一個完整的周期就會有254條pass,重訪周期為10 d，經過長江中游枝城水文站附近的軌跡為pass12。枝城水文站實測日平均數據(2008-07～2009-12)來源于長江水利委員會(http:∥www.cjw.gov.cn)，宜昌氣象站日降水量數據來源于國家氣象數據共享服務平臺(https:∥data.cma.cn)。

2 研究方法

2.1 波形重跟蹤算法

衛星測高波形是雷達脈沖信號回波功率的幾何表示，與測高儀觀測距離存在函數關系，且與反射表面的散射性質有關[6]。測高衛星自南半球向北半球運轉，當衛星軌道從海洋經過內陸水域時，接收到的測高回波波形由規則低噪聲逐漸向不規則強噪聲過渡。測高回波波形大致有規則波形(圖3(a))、尖錐波形(圖3(b))、復雜波形(圖3(c))3種模式，其中規則波形是海洋回波波形的主要表現形式，形狀近似于規則的布朗模型且波形前緣噪聲很小；尖錐波形、復雜波形則是內陸水體回波波形的主要表現形式。當衛星同一軌跡的不同時期經過內陸水域時，回波會以2種形式出現，可以看到復雜波形的前緣噪聲很大且出現多個波峰。

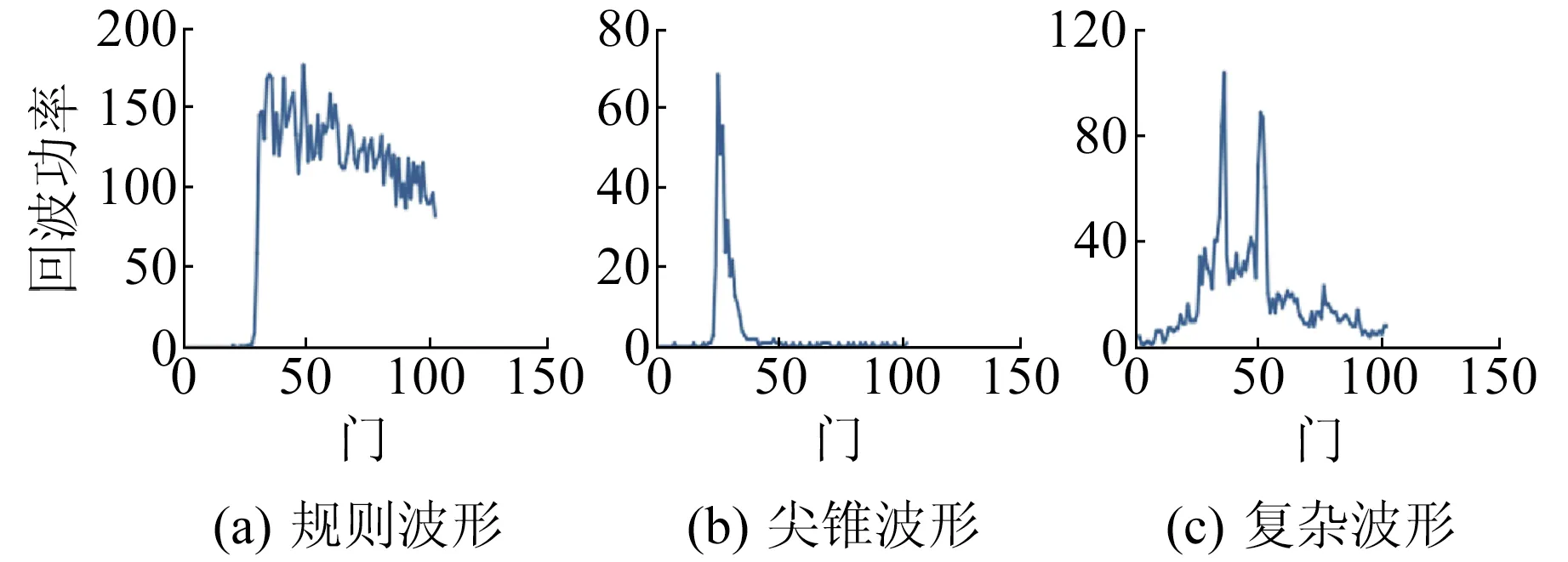
圖3 不同區域內的衛星測高波形

通過重跟蹤算法對衛星測高波形進行模擬，找到波形上升前緣的中點，其與Jason-2衛星預設跟蹤門(值為32)之間的差值為距離改正值，最后對衛星至水體表面的距離進行重新修正即為波形重跟蹤。當前波形重跟蹤算法在尋找內陸水體復雜波形的前緣中點時面臨困難，為此本文構建了一種基于主波峰的自適應波形重跟蹤算法(AMWRT)對衛星測高波形進行重跟蹤，并與較為經典的重心偏移法(OCOG)[6]及10%、20%、50%三種不同閾值水平的閾值法(threshold)[10]進行對比。

AMWRT算法具體包括3個步驟(圖4)。

圖4 AMWRT算法流程

1)提取主峰波形[11]：

(1)

(2)

(3)

(4)

2)對主波峰進行波形重跟蹤，即對上述提取的主波峰波形進行OCOG和threshold法10%、20%、50%及70%四種不同閾值水平的波形重跟蹤。

3)以IMP評判指標對上述同一時期波形重跟蹤算法獲得的水位值進行判優：

(5)

式中，σraw為波形重跟蹤前水位的標準差，σre為波形重跟蹤后水位的標準差，IMP值越大則表明測高點瞬時水位值之間的差值越小。以IMP最大值的波形重跟蹤算法得到的結果作為AMWRT算法的結果。

2.2 衛星測高數據獲取河流水位

使用Jason-2衛星數據20 Hz的SGDR波形數據，根據上述波形重跟蹤算法，計算獲得改正后的觀測距離(Ran)。河流自由水面的高程[12]計算公式為：

H=Alt-Ran-Hei-ΔCCor

(6)

式中，H為河流水位高程，Alt為測高儀的橢球高，Ran為雷達高度計至水面的觀測距離，Hei為大地基準面相對于參考橢球面的高度，ΔCCor為各項觀測誤差修正。由于河流的面積較小，與海洋相比受海潮、逆氣壓、高頻風壓力和壓力反饋等的影響很小，可忽略[13]。ΔCCor計算公式為：

ΔCCor=Wet+Dry+Iono+Solid+Pol

(7)

式中，Wet為濕對流層修正，Dry為干對流層修正，Iono為電離層修正，Solid為固體潮修正，Pol為極潮修正。

利用雷達測高工具箱BRAT(basic radar altimetry toolbox)軟件對SGDR數據進行以下處理：1)提取出河流范圍內的所有點；2)保證測高儀所觀測的高度有效；3)對各修正項數值范圍進行有效設定[14]，確保各項改正數據在有效范圍內；4)提取波形數據。

2.3 水位高程基準轉換

利用AMWRT算法對測距值進行重新修正，通過水位計算公式獲得瞬時水位。利用連續優質點數據質量篩選辦法[3]對瞬時水位進行數據篩選，然后取水位均值，獲得區域內某一時期的衛星測高水位。由于衛星測高水位(基于EGM96大地水準面)與枝城水文站實測水位(基于吳淞水系水準面)的基準面不同，為進行對比分析，需要獲取垂直基準偏差[10]。對衛星測高水位與實測水位進行線性擬合(擬合斜率為1)，將衛星測高水位歸算至枝城水文站基準面下，結果如圖5所示，可以看出，二者具有很強的相關性。由擬合方程可知，EGM96大地水準面比吳淞水系水準面起點高1.61 m。

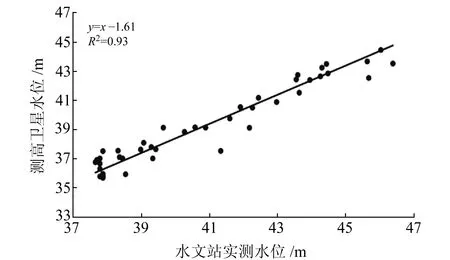
圖5 衛星測高水位與實測水位散點對比

3 結果分析

3.1 河流水位精度分析

Jason-2衛星測高數據經6種重跟蹤算法(AMWRT算法中threshold_0.7(即閾值水平為70%，下同)僅針對特殊波形，故未考慮)處理后，獲得長江中游2008-07～2009-12的瞬時水位。AMWRT算法在該時期的平均水位為40.79 m，與實測水位40.81 m最為接近，threshold_0.1、threshold_0.2、threshold_0.5及GDR(原數據自帶的重跟蹤算法)、OCOG法獲得的平均水位依次為41.15 m、40.89 m、40.25 m、40.20 m、40.13 m。

月內長江中游日平均水位變化較大，最低水位為39.43 m，最高水位為44.31 m，變化幅度可達4.88 m。圖6顯示，不同波形重跟蹤算法獲得的水位在變化趨勢上與實測水位高度一致，二者擬合系數在0.73～0.93之間，但均出現了不同程度的偏離(圖7)。與實測水位相比，除AMWRT算法外，其他算法在2008-11-08得到的水位均被不同程度地高估(圖6紅色方框)，其原因在于該時期岸邊地物目標距離衛星更近，使得回波波形中陸地反射信號在波形中占主導地位，形成的第1個上升強回波容易被經典重跟蹤算法認為是水體反射形成的回波，從而形成誤差。

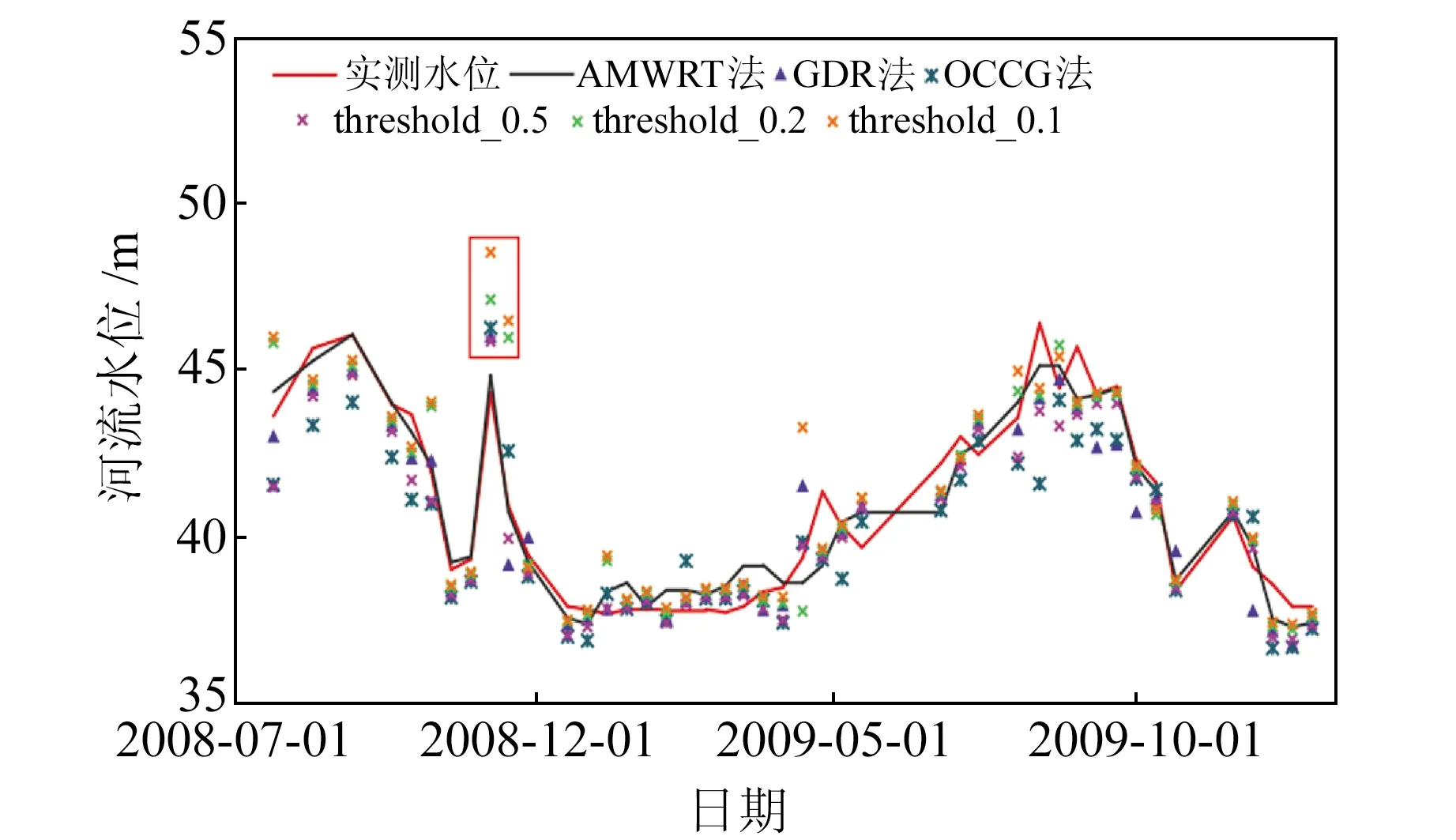
圖6 測高與實測月水位對比

圖7顯示了OCOG法及threshold法在10%、20%和50%閾值水平下得到的衛星測高水位與枝城水文站日平均水位的對比，可以看出，其精度差異較大，MAE介于0.55～1.41 m之間，RMSE介于0.72～1.61 m之間。GDR算法獲取的衛星測高水位MAE為1.15 m，表明在長江中游區域對波形數據進行重跟蹤十分必要。就threshold法而言，相對于其他閾值水平，50%閾值水平的重跟蹤算法的精度改善效果更好，MAE為0.845 m，RMSE為1.04 m。相比于經典算法，AMWRT算法表現最好，獲得的河流水位精度最高，MAE為0.55 m，RMSE為0.72 m。

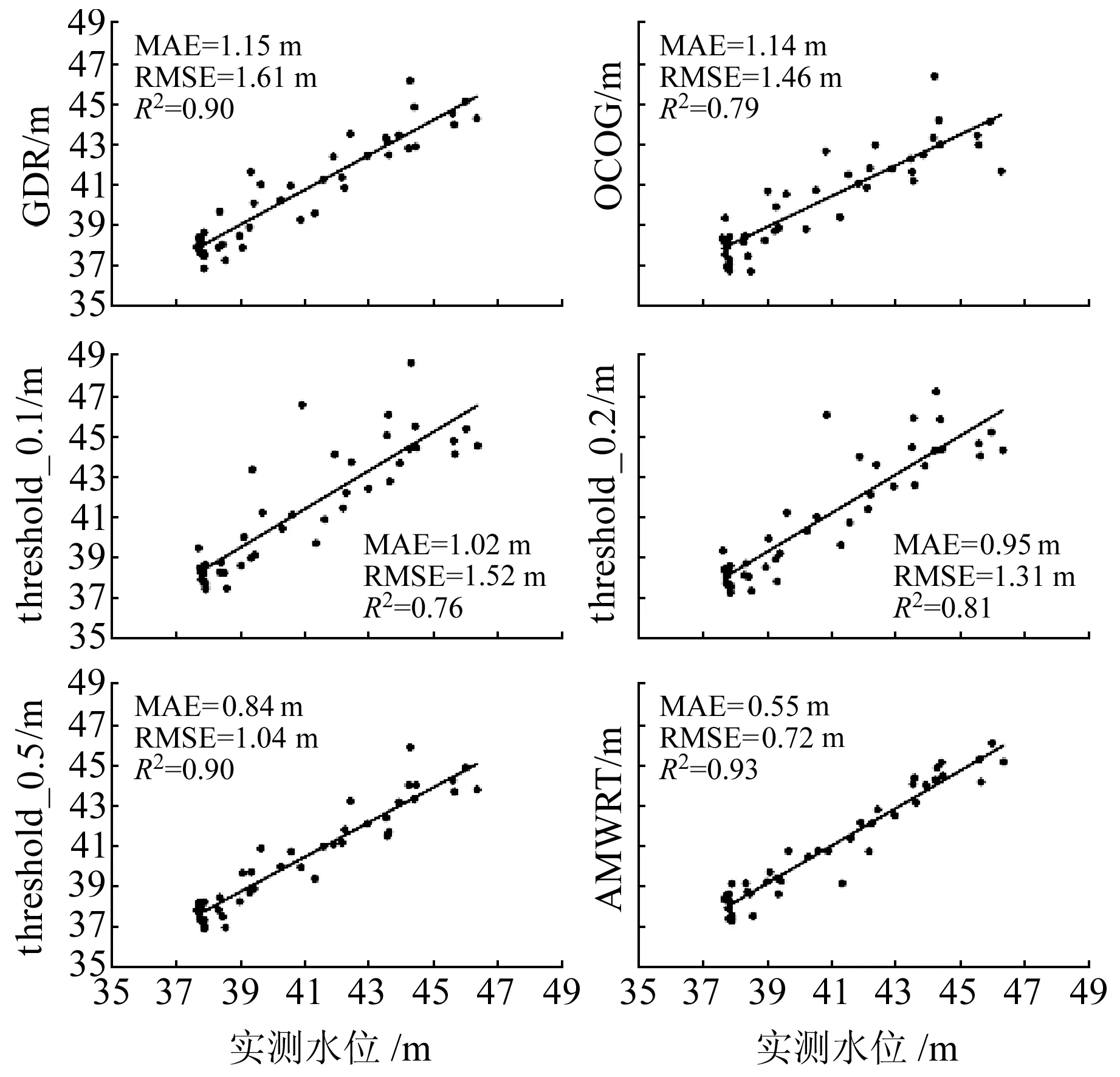
圖7 衛星測高與實測日平均水位對比

不同波形重跟蹤算法得到的水位與實測水位的偏差對比如表1所示，可以看出，在最大、最小差值變化幅度中，經典的重跟蹤算法得到的水位與實測水位偏離較大，而AMWRT算法得到的水位偏差都較為穩定。就絕對平均誤差而言，除AMWRT算法外，其他重跟蹤算法的精度都在1 m左右，其原因可能在于，典型的重跟蹤算法在復雜的內陸水域往往會被衛星測高波形前緣的熱噪聲所影響，從而導致尋找波形上升前緣的位置與實際位置產生較大的偏離。由于AMWRT算法對主波峰的開始閾值進行了調整，可以減少回波波形上升前緣的熱噪聲對波形重跟蹤結果的影響，故AMWRT算法表現最好。

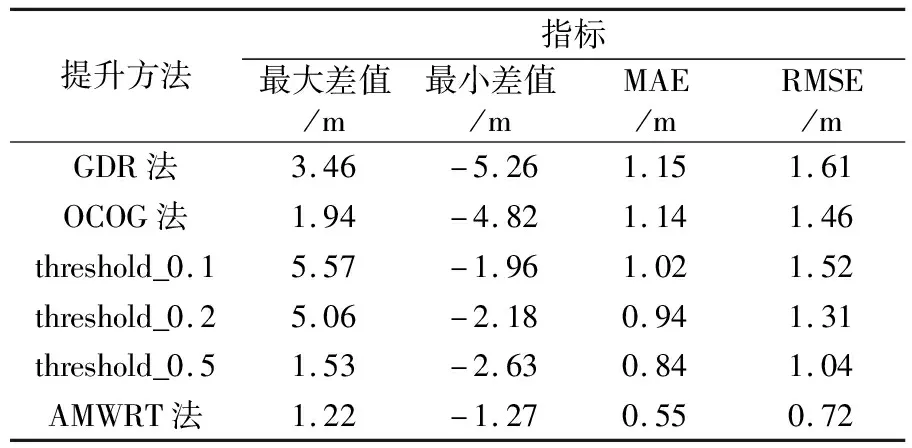
表1 波形重跟蹤算法精度分析

AMWRT算法獲得的長江中游水位MAE在0.55 m左右波動，如圖8所示，隨著實測水位的降低，衛星測高水位的相對誤差(RB)隨之升高。其原因在于：1)受長江中游周圍地形的影響，河流水位降低會導致反射波的上升前緣之前和之后都容易出現回波，且由于岸邊物體的反射率與水體發射率不同，波形中多個波峰的強度也不同；2)雷達高度計的腳印大小與衛星高度、反射面坡度及粗糙度有關。Jason-2測高衛星中心腳印點的直徑約為2～4 km[15]，而與平坦寬闊海域相比，長江中游河流寬度較小，當河流水位較低時，探測區水域均質性降低，測高回波中陸地污染影響增強，導致河流的測高衛星回波更為復雜。在進行波形重追蹤時，會出現難以正確找到波形上升前緣的情況，故降低了衛星測高數據的精度。

圖8 衛星測高水位誤差隨實測水位變化

3.2 河流水位變化與降雨量的關系

將AMWRT算法與數據質量等級篩選方法[3]相結合，計算2008-07～2016-08月平均水位序列。如圖9所示，長江中游月平均降雨量與水位都有明顯的季節性特征，二者呈正相關關系，相關系數為0.18，并通過了顯著性水平檢驗。長江中游水位變化較為劇烈，可能在一定程度上受降雨量的影響。由2008～2016年月平均水位變化可知，年內最高水位在降水集中期(7～8月)，最低水位在11月至次年4月。

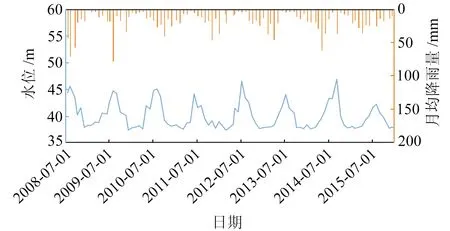
圖9 衛星測高水位與月降水對比

4 討 論

在長江中游的水位監測中，AMWRT算法在衛星測高精度方面取得了不錯的效果，其MAE為0.55 m，RMSE為0.72 m，與經典波形重跟蹤算法中表現最好的threshold_0.5(MAE為0.84 m，RMSE為1.04 m)相比提高了30%。河流周邊復雜的地形地物及水位較低時水域均質性差均會導致復雜波形的出現，而AMWRT算法在處理較為復雜的波形數據時比其他重跟蹤算法表現更好。王紅等[14]基于Jason-2衛星GDR數據獲得的水位在相關分析中的相關系數達0.93，而本文利用AMWRT重跟蹤算法對波形進行重跟蹤，結果與實測水位的相關系數達0.96。就衛星測高水位的精度提升而言，原數據自帶的重跟蹤算法與其他算法相比表現最差，說明波形重跟蹤算法對數據精度的提升具有重要意義。另外，由于數據篩選方法的不同，最終結果也會出現一定的差異。從本文算法的應用效果來看，AMWRT算法在表面寬度不大的河流區域的表現優于經典重跟蹤算法。

由于衛星測高技術主要應用于寬闊的海洋及冰川區域，測高衛星在內陸水體的監測精度有待提升。而本文研究僅考慮了部分誤差校正，且由衛星攝動影響產生的軌道誤差會影響衛星測高數據的最終精度。但由于衛星測高技術的優點明顯，對于偏遠且缺乏水位資料的地區而言，建立長時間水位變化序列仍具有重要意義。本文算法是否適用于不同區域類型的水位監測，后續需結合不同區域河流及多種衛星測高數據進行進一步檢驗。

5 結 語

本文利用Jason-2衛星SGDR數據進行波形重跟蹤，結合數據篩選方法提升衛星測高數據的精度，獲取2008-07～2016-09水位變化序列，分析了長江中游水位變化與降雨量的關系，并基于實測水位數據對不同的波形重跟蹤算法進行精度評價。主要結論如下：

1)基于Jason-2衛星 SGDR數據集中的GDR數據得到的水位與實測水位相比，在長時間水位序列變化上趨勢一致，但GDR數據自帶的重跟蹤算法獲得的水位在精度改善效果上仍有待提升，其MAE為1.15 m，RMSE為1.61 m。

2)AMWRT算法相較于其他重跟蹤算法表現最好，MAE為0.55 m，RMSE為0.72 m；而經典的重跟蹤算法threshold_0.5的MAE為0.84 m，RMSE為1.04 m。

3)長江中游的月平均水位與降雨量有一定的相關性，且年內月平均水位變化較大。