一種用于優化LC-DAB級聯系統穩定性的 虛擬阻抗控制技術

周兵凱 楊曉峰 李繼成 農仁飚 鄭瓊林

（北京交通大學電氣工程學院 北京 100044）

0 引言

雙有源橋（Dual-Active-Bridge, DAB）變換器具有高效率、能量雙向傳輸及電氣隔離等優勢，近年來在直流電能傳輸及變換領域受到了廣泛的關 注[1-3]。此外，DAB變換器還主要被應用于儲能設備、電動汽車、光伏及能量路由器等場合[4-6]。為改善DAB變換器的抗干擾能力及輸入電流質量，具有LC輸入濾波的DAB變換器（LC-DAB）級聯型拓撲近年來受到了關注[7]。然而，LC-DAB級聯型系統較易出現振蕩和不穩定問題。鑒于LC濾波器自身所存在的特征諧振點及LC與DAB變換器阻抗之間的相互作用，易造成LC-DAB級聯系統的輸入電容電壓發生振蕩現象，且類似的問題也出現在其他直流和交流級聯系統中[8-11]，因此分析LC-DAB級聯系統的穩定性尤為重要。

基于阻抗的穩定性判據最早被R. D. Middlebrook提出，已成為分析級聯系統穩定性的基礎之一[12]。然而，Middlebrook穩定性判據相對保守，要求負載變換器的輸入阻抗在全頻率范圍內均大于源變換器的輸出阻抗，在實際應用中較為嚴苛。因此，相關學者提出了最小環路增益Tm的概念，即源變換器的輸出阻抗與負載變換器的輸入阻抗之比應滿足奈奎斯特穩定性判據[13-14]，以確保級聯系統的穩定性。相關技術已經被提出用于改善源變換器的輸出阻抗和負載變換器的輸入阻抗。目前的主要解決方案可分為無源阻尼方式和有源阻尼方式[15]兩大類。

無源阻尼方式需在原來電路的基礎上增加一個或多個無源元件，如在直流母線濾波器側并聯電阻或電容用以改變源變換器的阻抗[16]，然而這會增加額外成本和功率損耗。此外，由于電解電容預期壽命較短，所以在高可靠性應用中需避免使用較大的電解電容[17]。

有源阻尼控制策略研究方面，文獻[18]通過在源和負載變換器之間引入緩沖變換器以優化輸入和輸出阻抗之間的相互影響，但需重新設計主電路，這對于模塊化設計的電路十分耗時。文獻[19-20]通過有源阻尼方法降低源變換器的輸出阻抗從而滿足基于阻抗模型的穩定性判據，減小系統振蕩的同時增強了穩定性。文獻[21]通過控制手段在負載變換器中添加虛擬電阻或電容器進而改變負載變換器的輸入阻抗，使得系統重新恢復至穩定狀態。但上述解決方案在LC-DAB級聯系統中的應用少有文獻 研究。

為改善LC-DAB級聯系統的穩定性，本文首先建立了DAB變換器狀態空間平均化小信號數學模型，并驗證了所推導的閉環輸入阻抗模型的正確性。基于此，分析了LC-DAB級聯系統振蕩現象產生原因及LC濾波器參數對系統穩定性的影響，分別提出了一種基于DAB變換器一次側電容電壓的并聯虛擬阻抗（Parallel Virtual Impedance, PVI）和一次電流的串聯虛擬阻抗（Series Virtual Impedance, SVI）控制策略。最終使得LC-DAB級聯系統在全功率范圍內均無振蕩且能夠穩定運行，并通過實驗對上述理論及控制進行驗證。

1 LC-DAB級聯系統

圖1為LC-DAB級聯系統主電路拓撲，與典型DAB變換器相比，在電源側串聯接入濾波電感Lf及內阻Rf，與一次側電容Cf構成二階LC低通濾波器，進而形成級聯系統。前級為LC濾波器，后級為DAB變換器，Uin與iin分別為電源電壓和LC-DAB的輸入電流。DAB變換器主要由兩個H橋（H1和H2）和隔離變壓器T組成。其中，一次側和二次側電容電壓分別為Udc和Uout。一次電流和二次電流分別為iLp和iLs。iL和iout分別為電感電流和負載電流，H1輸出電壓和H2輸入電壓分別為Uab和Ucd，一次側電容和二次側電容電流分別為iCf和iCout。規定圖1中箭頭方向為電流正方向，L為變壓器漏感和輔助電感之和，Cout為二次側電容，RL為負載等效電阻，變壓器電壓比為n。

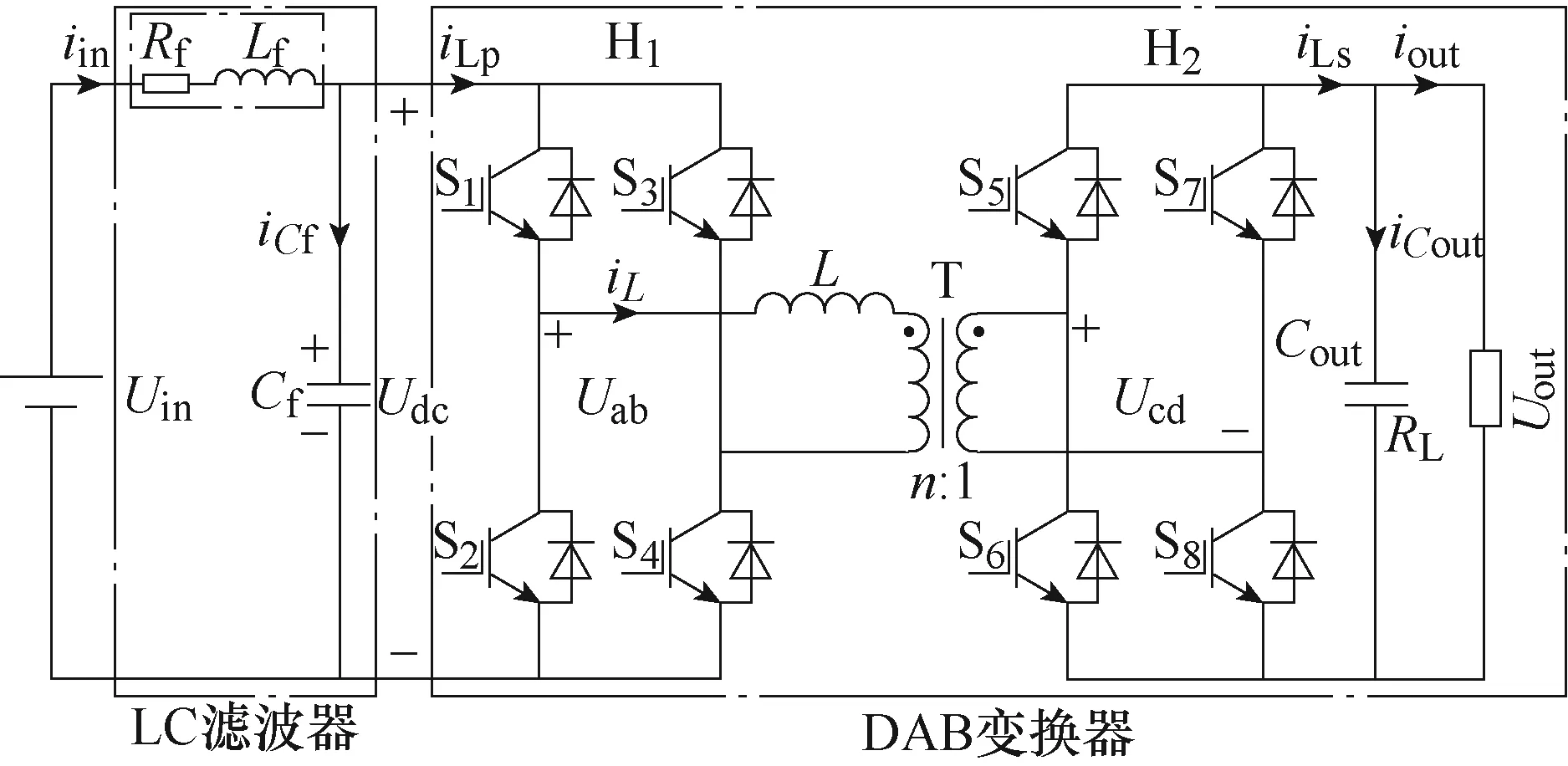
圖1 LC-DAB拓撲 Fig.1 Topology of LC-DAB

由圖1可知，用以描述LC-DAB級聯系統的電路微分方程可分別表示為

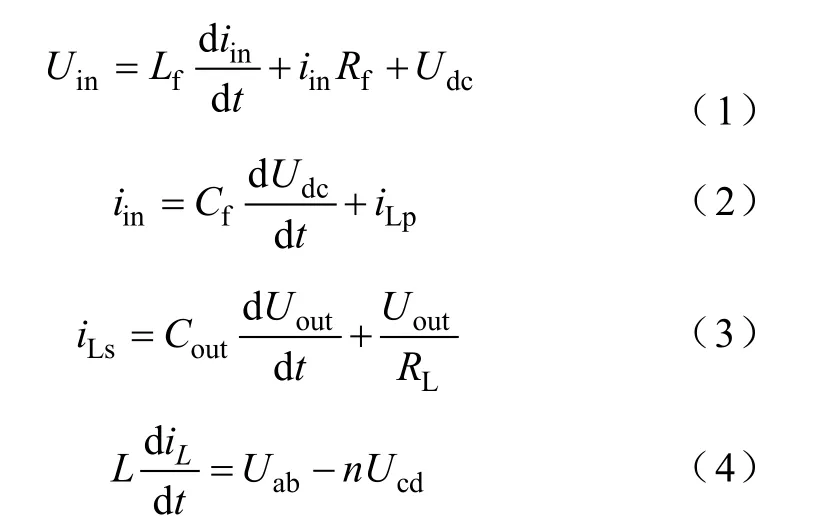
DAB變換器在單移相（Single Phase Shift, SPS）控制下的工作波形如圖2所示，其中，定義Ths為半個開關周期，D為H1與H2之間的移相比，0≤D≤1。

由圖2可知，在穩態運行工況下，DAB變換器的傳輸功率Pt與移相比D之間的關系[22]為

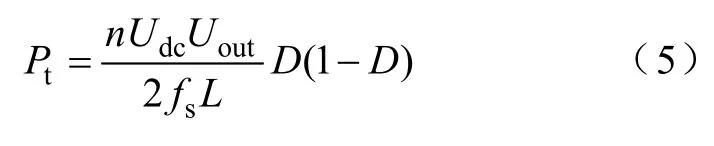
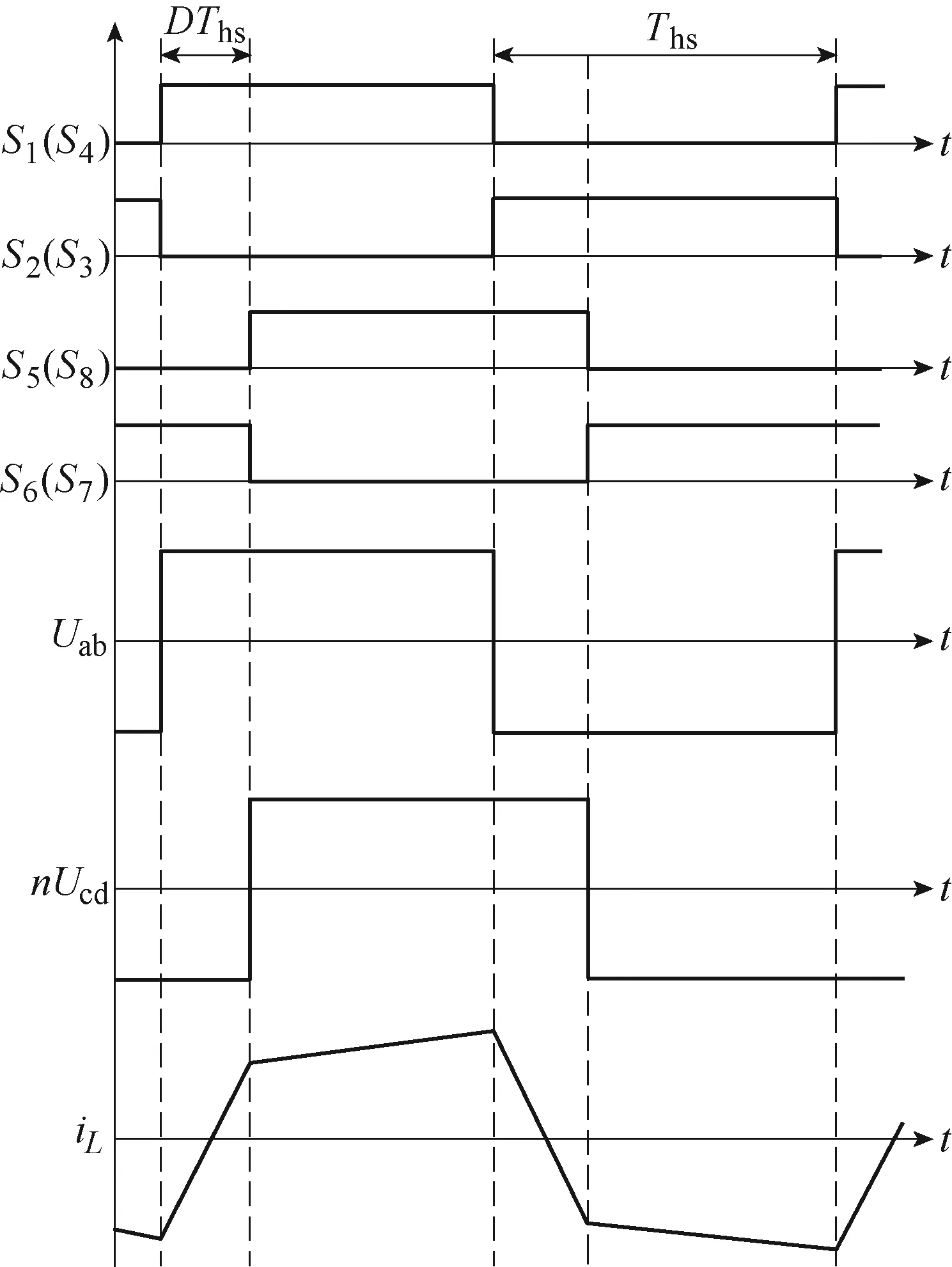
圖2 SPS控制下DAB變換器工作波形 Fig.2 Working waveforms of DAB converter under SPS control

其中

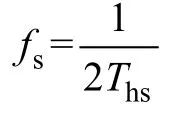
式中，fs為開關頻率。

2 LC-DAB系統阻抗模型與穩定性分析

2.1 DAB變換器平均化小信號阻抗模型

通過對DAB變換器一次電流iLp平均化，在一個開關周期內可得

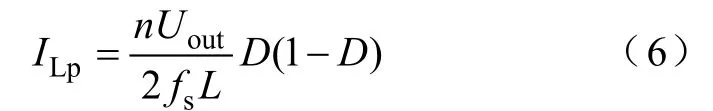
同理，一個開關周期內，二次側平均輸出電流ILs可表示為

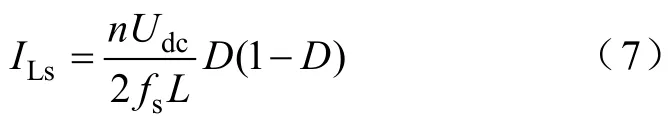
因此根據式（6）和式（7），可得到DAB變換器降階平均化模型的等效電路如圖3所示。

圖3 DAB變換器平均值模型等效電路 Fig.3 A verage model of DAB converter

同時將式（6）和式（7）分別進行小擾動和線性化得到DAB變換器的小信號數學模型為

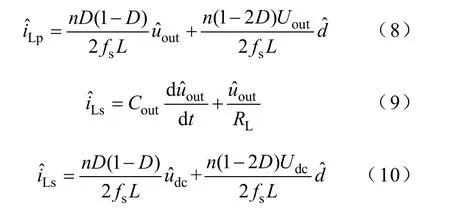
可得到DAB變換器小信號模型的等效電路如圖4所示。

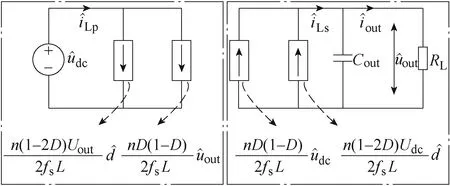
圖4 DAB變換器小信號模型等效電路 Fig.4 Small signal model of the DAB converter

根據圖4可得到DAB變換器的開環小信號輸出阻抗ZoutDAB_OL(s)為

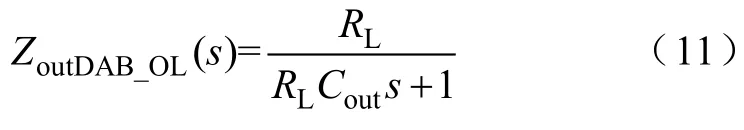
由此，可得DAB變換器的小信號模型控制框圖如圖5所示，圖中，GvDAB(s)為輸出電壓控制器，本文采用PI控制。

圖5 DAB變換器小信號模型控制框圖 Fig.5 Small signal model control block diagram of DAB converter

進而可推導得出閉環控制下DAB變換器的輸入導納YinDAB_CL(s)為

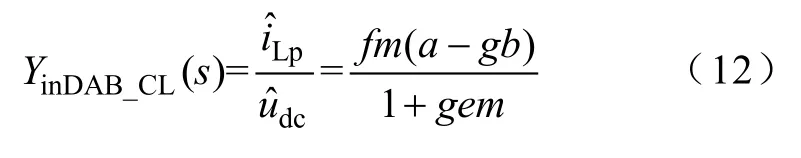
其中

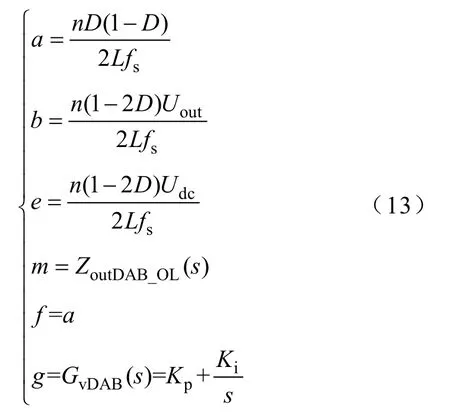
式中，Kp和Ki分別為PI控制器比例系數和積分系數。

由此可得到DAB變換器的閉環輸入阻抗ZinDAB_CL為

2.2 DAB阻抗模型驗證

為驗證所推導阻抗模型的正確性，本文采用測試信號法。通過在DAB變換器一次側電容電壓Udc側疊加小信號干擾源，測量一次電流iLp的小信號響應，最后計算得到在各個頻率點的阻抗并與理論推導阻抗模型進行對比。阻抗測量及LC-DAB級聯系統小信號簡化電路如圖6所示。其中，阻抗測量電路如圖6a所示，LC-DAB級聯系統仿真參數見 表1。

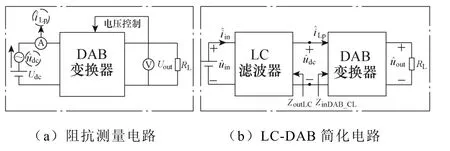
圖6 阻抗測量及LC-DAB級聯系統小信號簡化電路 Fig.6 Impedance measurement and LC-DAB cascaded system small signal simplification circuit

DAB變換器閉環輸入阻抗小信號模型與仿真測量阻抗特性曲線如圖7所示。實線為根據數學模型推導得到的理論分析值，米字狀為通過電路仿真所得到的輸入阻抗測量值，從圖中可知，仿真測試與理論分析結果基本一致。驗證了所推導的輸入阻抗模型的正確性，對進一步分析LC-DAB級聯系統的振蕩及穩定性具有重要的指導意義。

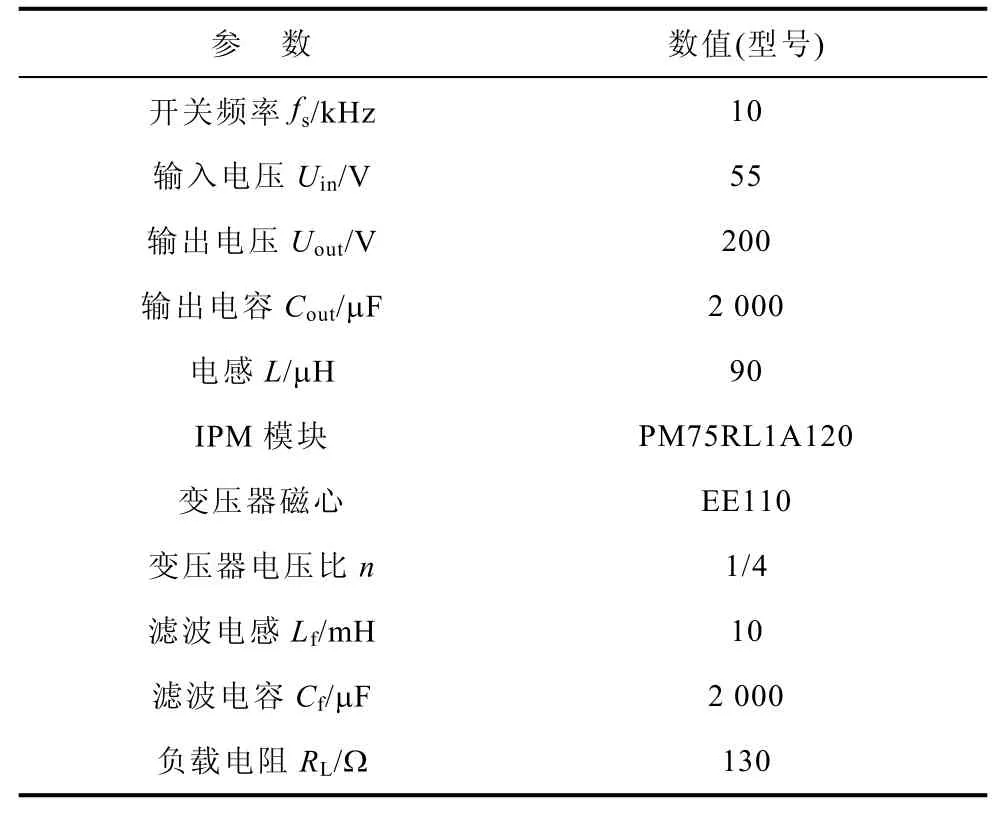
表1 LC-DAB仿真參數 Tab.1 The simulation parameters of LC-DAB

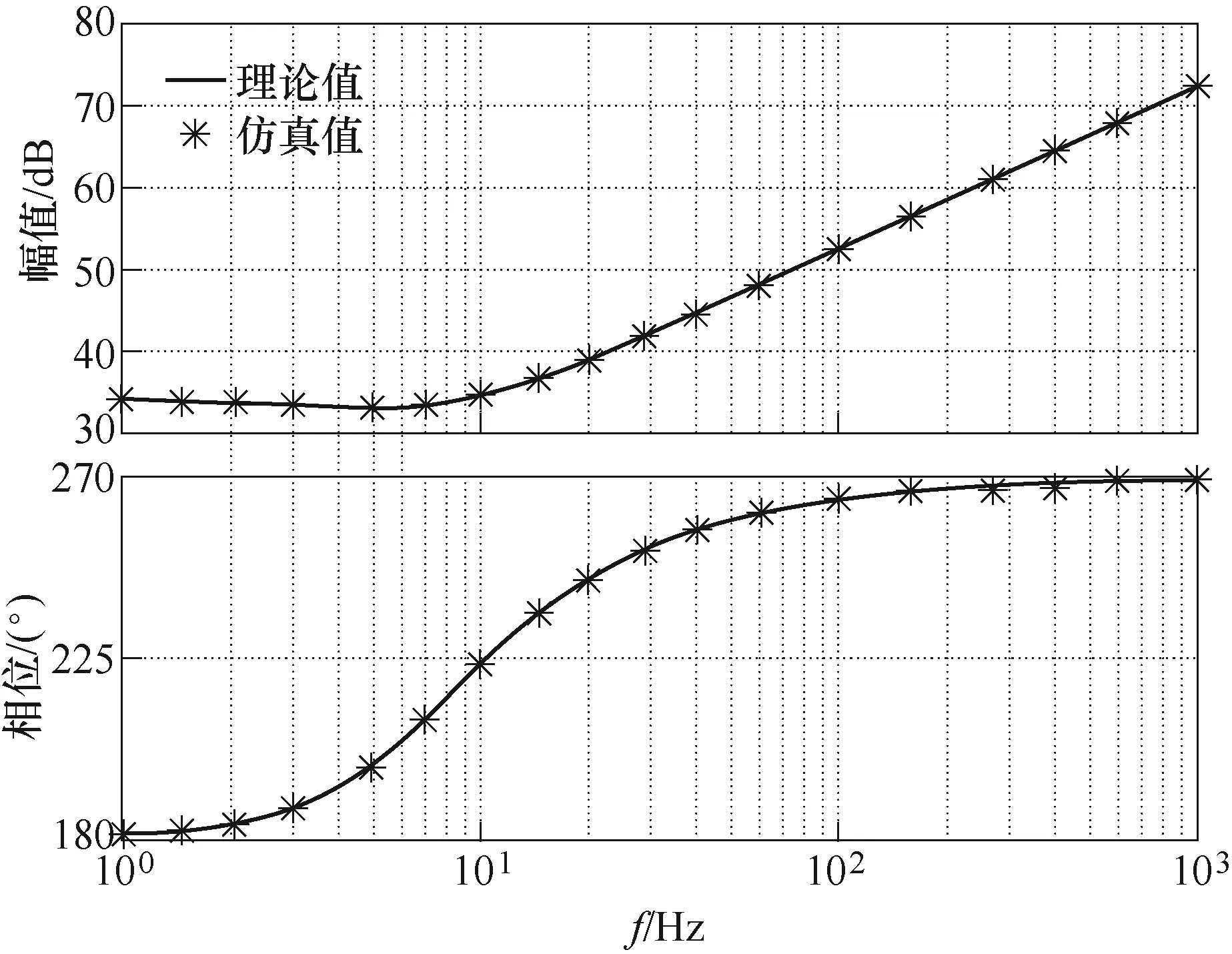
圖7 DAB變換器理論分析與仿真測量阻抗對比 Fig.7 Theoretical analysis and simulation measurement impedance comparison diagram of DAB converter

2.3 LC-DAB穩定性分析

LC-DAB的穩定性可根據級聯系統阻抗模型穩定性判據進行分析。當源變換器為電壓控制時，阻抗比Tm可表示為Tm=Zout/Zin；當源變換器為電流控制時，Tm的表達式為Tm=Zin/Zout。若Tm滿足奈奎斯特穩定性判據，則級聯系統穩定；否則級聯系統不穩定。本文級聯系統小信號簡化電路如圖6b所示，因此LC-DAB級聯型拓撲的阻抗比TmDAB可表示為

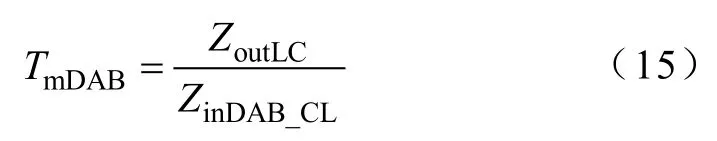
式中，ZoutLC為LC濾波器輸出阻抗，可根據式（1）和式（2）推導得出，有

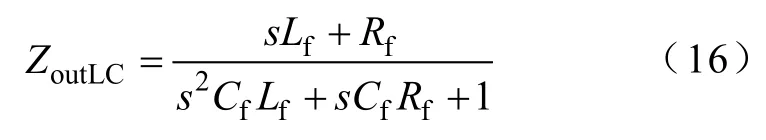
同時可得到LC濾波器的諧振頻率fr可表示為

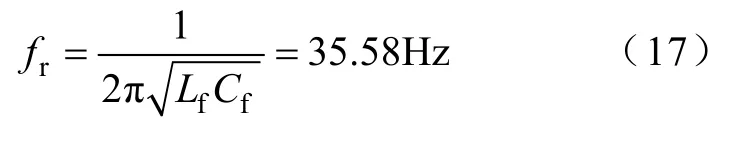
DAB變換器閉環輸入阻抗與LC濾波器輸出阻抗特性曲線如圖8所示。當DAB變換器運行在半載工況下時，輸入阻抗|ZinDAB_CL|恒大于LC輸出阻抗|ZoutLC|，兩者曲線完全分離不存在交截，因此在此運行工況下級聯系統穩定；但是當運行在全載工況下時，|ZinDAB_CL|減小并且與|ZoutLC|存在交叉，|ZoutLC|最大交叉點值所對應頻率為LC諧振頻率fr=35.58Hz；同時因為在阻抗幅值的交叉范圍內，兩者相位差的絕對值恒大于180°，因此LC-DAB級聯系統在全載運行工況下易發生振蕩及不穩定。

圖8 LC-DAB級聯系統ZinDAB_CL與ZoutLC阻抗特性曲線 Fig.8 Impedance characteristics of ZinDAB_CL and ZoutLC in the cascaded system of LC-DAB

同樣，根據阻抗比TmDAB可得到LC-DAB級聯系統的Nyquist曲線如圖9所示。當LC-DAB運行在半載工況下時，Nyquist曲線整體位于（?1, j0）點右側，未包圍（?1, j0）點，根據穩定性判據可知級聯系統處于穩定狀態。但是，當LC-DAB運行在全載工況下時，Nyquist曲線包圍了（?1, j0）點，因此級聯系統在全載運行工況下會出現振蕩甚至發散。以上兩種分析方法均說明了LC-DAB級聯系統在全載工況下運行時易出現振蕩及不穩定的問題。

為解決上述振蕩及不穩定問題，首先分析了LC濾波器參數對LC-DAB系統穩定性的影響。級聯系統隨著濾波電感Lf與濾波電容Cf變化的Nyquist曲線分別如圖10a和圖10b所示。由圖10a可知，隨著Lf的逐漸增加，Nyquist曲線越容易包圍（?1, j0）點，LC-DAB級聯系統越容易發生振蕩和不穩定。 由圖10b可知，隨著Cf的逐漸增大，Nyquist曲線越遠離（?1, j0）點，LC-DAB級聯系統越穩定。

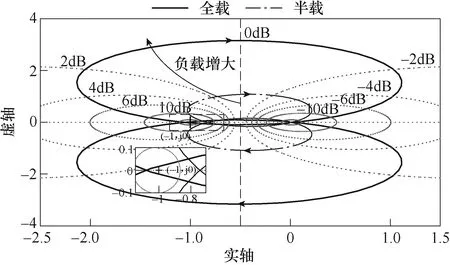
圖9 LC-DAB級聯系統Nyquist曲線 Fig.9 Nyquist curves of LC-DAB cascaded system

圖10 不同參數下LC-DAB級聯系統Nyquist曲線 Fig.10 Nyquist curves of LC-DAB cascaded system under different parameters

由此可知，在設計LC濾波器時，當其截止頻率確定后，選取電感和電容參數時應該在合適的范圍內增加Cf、減小Lf，從而在硬件設計的源頭上降低LC-DAB級聯系統的振蕩并增強其穩定性。

調整LC濾波器硬件參數的方法較為簡單，但實際系統的實施難度大。另一種方式為采用優化LC-DAB級聯系統控制環路的思路，使得在特定頻率范圍內令輸入阻抗幅值增加（輸入導納減小），最終實現兩者阻抗幅值曲線完全分離，調節級聯系統重新恢復至穩定狀態。此方案只需對系統的控制策略進行優化，并不需要硬件設備的更換，在具有更好經濟性的同時提高了控制系統的靈活性。因此本文后續重點對其展開研究和分析。

由圖8可知，級聯系統阻抗幅值特性曲線的交叉主要出現在中低頻范圍內，故優化DAB變換器中低頻段的輸入阻抗十分重要。可通過在原控制回路中增加一個前饋或者反饋路徑，因為前饋或者反饋路徑可以分別改變輸入阻抗的分母或分子。基于以上思路，本文分別提出了PVI和SVI控制策略。

3 LC-DAB系統穩定性優化

3.1 并聯虛擬阻抗控制

根據圖5所示的DAB變換器小信號模型控制框圖，可知從一次側電容電壓dc?u到一次電流存在兩條前饋路徑。若再增加一個前饋路徑，則可能在一定程度上減小YinDAB_CL(s)的幅度，從而增大輸入阻抗的幅值，使得與LC輸出阻抗幅值特性曲線完全分離。

LC-DAB級聯系統并聯虛擬阻抗控制策略如圖11所示，附加基于一次側電容電壓的PVI控制環被引入。其中，前饋控制器由Gpvir(s)表示，可得加入PVI之后的DAB變換器輸入導納Yinpvir_DAB_CL(s)可表示為

其中

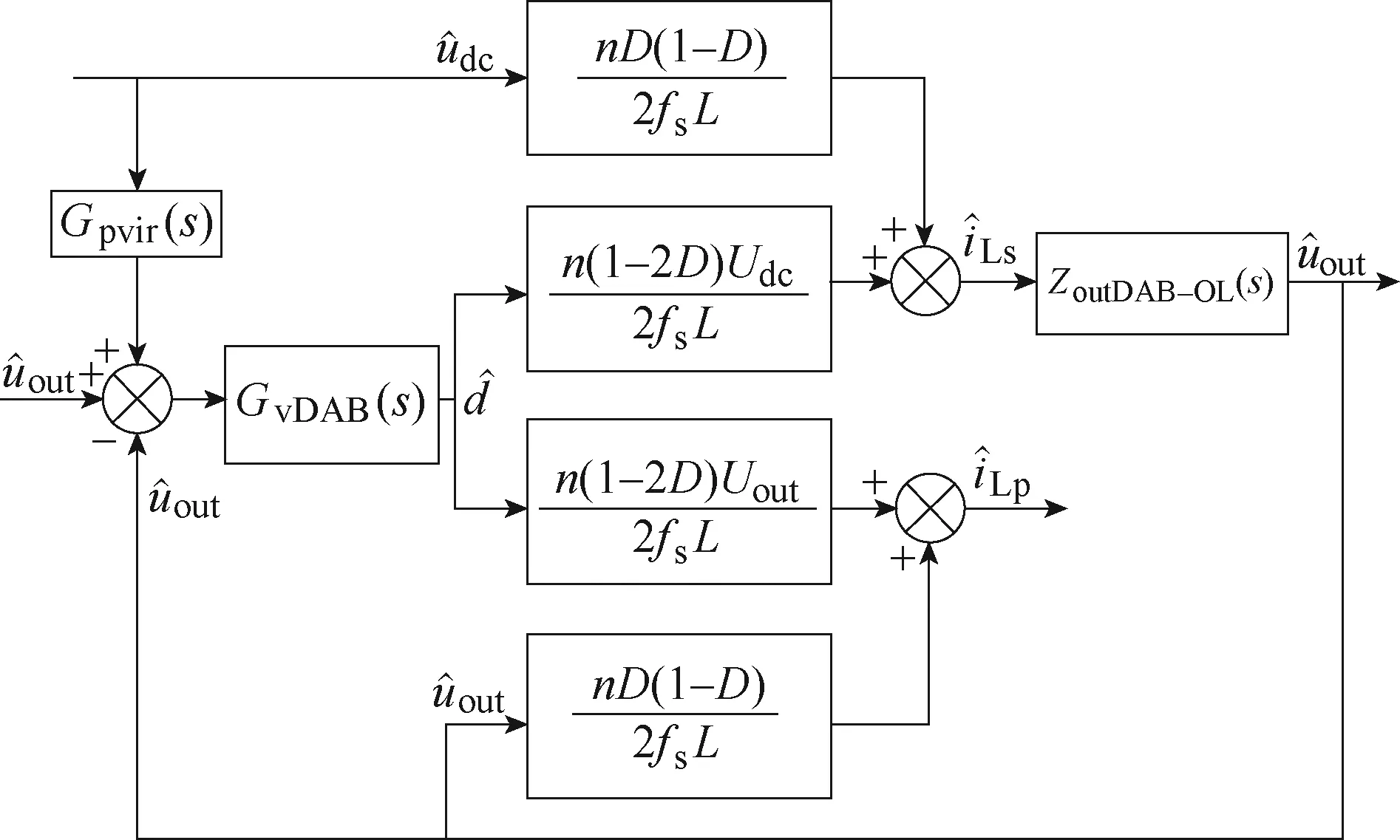
圖11 LC-DAB級聯系統并聯虛擬阻抗控制策略 Fig.11 Parallel virtual impedance control strategy for LC-DAB cascaded system

式中，Ypvir_DAB(s)為與DAB變換器中YinDAB_CL(s)所并聯的等效虛擬導納。

因此可得到加入PVI控制環之后的DAB變換器輸入阻抗Zinpvir_DAB為

由圖8可知，ZoutLC的最大值出現在LC濾波器諧振頻率fr處，當頻率超過fr時，LC濾波器輸出阻抗幅值開始下降，最終將會保持在?20dB/dec的下降速度。然而DAB變換器輸入阻抗幅值在中高頻率（f≥1kHz）范圍內以+20dB/dec上升，因此在高頻率范圍內兩者阻抗值一定不會再次出現交叉，從而不會再次導致級聯系統的振蕩及不穩定。可知在中低頻率范圍內增加DAB變換器的輸入阻抗十分重要，使得兩者阻抗幅值曲線完全分離。因此可得在中低頻率范圍內Ypvir_DAB(s)應滿足

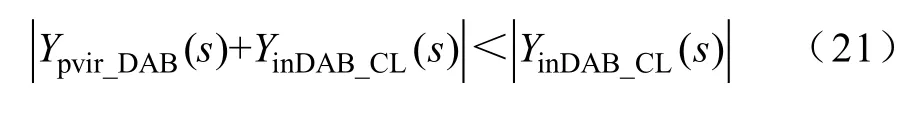
綜合考慮控制系統的復雜程度及數字芯片的處理能力，本文采用典型一階低通濾波器實現PVI控制器Gpvir(s)，具體表達式為

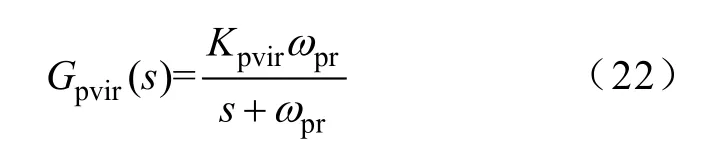
式中，Kpvir為PVI調節系數；ωpr為PVI低通濾波器截止角頻率。

由上述分析可得，加入PVI控制器之后，LC- DAB級聯系統阻抗特性曲線如圖12所示。當Kpvir從0逐漸增加至0.12時，Zinpvir_DAB的阻抗特性曲線逐漸向上平移，阻抗幅值逐漸增加。當Kpvir＞0.06時，輸入阻抗Zinpvir_DAB與LC輸出阻抗ZoutLC完全分離，系統振蕩消失且由不穩定狀態重新恢復至穩定。因此理論分析證明了本文所提出的PVI控制策略的有效性。

3.2 串聯虛擬阻抗控制

同理根據圖5所示的DAB變換器小信號模型，并且由第2.1節的分析可知，從一次側電容電壓到一次電流存在兩條前饋路徑。若再增加一個反饋路徑，則可能在一定程度上增加ZinDAB_CL的幅度，使得LC-DAB級聯系統的Nyquist曲線遠離（?1, j0）點，從而降低系統振蕩并優化其穩定性。

圖12 LC-DAB級聯系統Zinpvir_DAB與ZoutLC的 阻抗特性曲線 Fig.12 Impedance characteristics of Zinpvir_DAB and ZoutLC in the cascaded system of LC-DAB

LC-DAB級聯系統串聯虛擬阻抗控制策略如圖13所示，附加的基于一次電流的SVI控制環被引入。其中，反饋控制器由Gsvir(s)表示，可得加入SVI之 后的DAB變換器輸入阻抗Zinsvir_DAB_CL可表示為

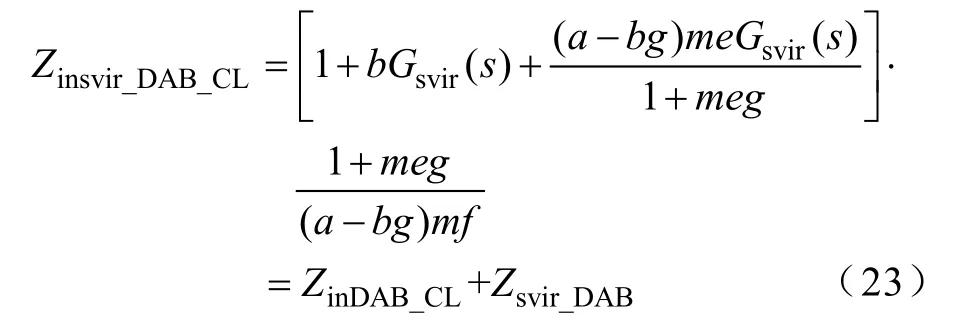
其中

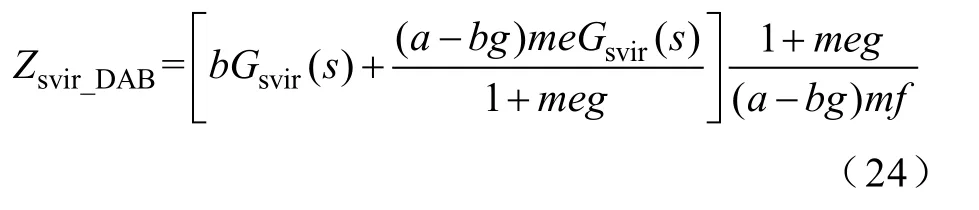
式中，Zsvir_DAB為與DAB變換器中ZinDAB_CL所串聯的等效虛擬阻抗。

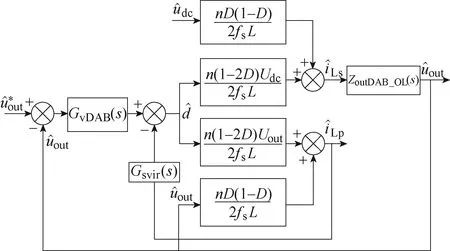
圖13 LC-DAB級聯系統串聯虛擬阻抗控制策略 Fig.13 Series virtual impedance control strategy for LC-DAB cascaded system

類似地，由前述分析可得在中低頻率范圍內Zsvir_DAB應滿足

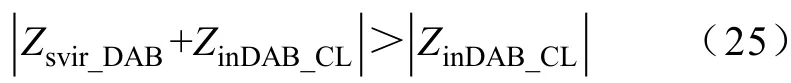
同樣地，采用典型一階低通濾波器實現SVI控制器Gsvir(s)，具體表達式為

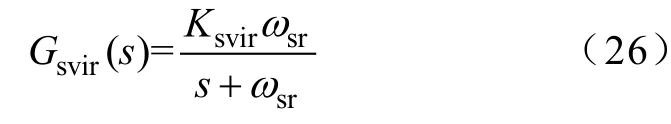
式中，Ksvir為SVI調節系數；ωsr為SVI低通濾波器截止角頻率。

由此可得加入SVI控制器之后，LC-DAB級聯系統的Nyquist曲線如圖14所示。當Ksvir從0逐漸增加至1.2時，Nyquist曲線逐漸呈現從包圍（?1, j0）點向與（?1, j0）點完全分離的變化趨勢。當Ksvir＞0.8時，Nyquist曲線完全不包圍（?1, j0）點，根據奈奎斯特系統穩定性判據可知，LC-DAB級聯系統由不穩定狀態重新恢復至穩定。因此理論分析同樣證明了SVI控制策略的有效性。

圖14 不同SVI調節系數下的LC-DAB級聯系統 Nyquist曲線 Fig.14 Nyquist curves of LC-DAB cascaded system with different SVI adjustment factors

根據以上分析可知，兩種控制策略均能夠有效地調節DAB變換器的輸入阻抗，減小了LC-DAB級聯系統的振蕩并提升了其穩定性。其中，兩種控制的不同之處為PVI控制需要一個額外的電壓傳感器測量DAB變換器的一次側電容電壓Udc，而SVI控制需要電流傳感器測量DAB一次電流iLp。下面分別對PVI和SVI控制進行驗證。

4 實驗驗證

為驗證本文所提出的PVI和SVI控制策略的有效性，本文以TMS320F28335為主控芯片搭建了LC-DAB級聯系統小功率實驗樣機。其中，實驗參數與仿真參數一致，可見表1。

4.1 LC-DAB系統振蕩現象

當LC-DAB系統輸入電壓Uin=55V，半載運行（功率為150W）和全載運行（功率為300W），在均未采用PVI和SVI控制策略時，電壓電流波形如圖15所示。

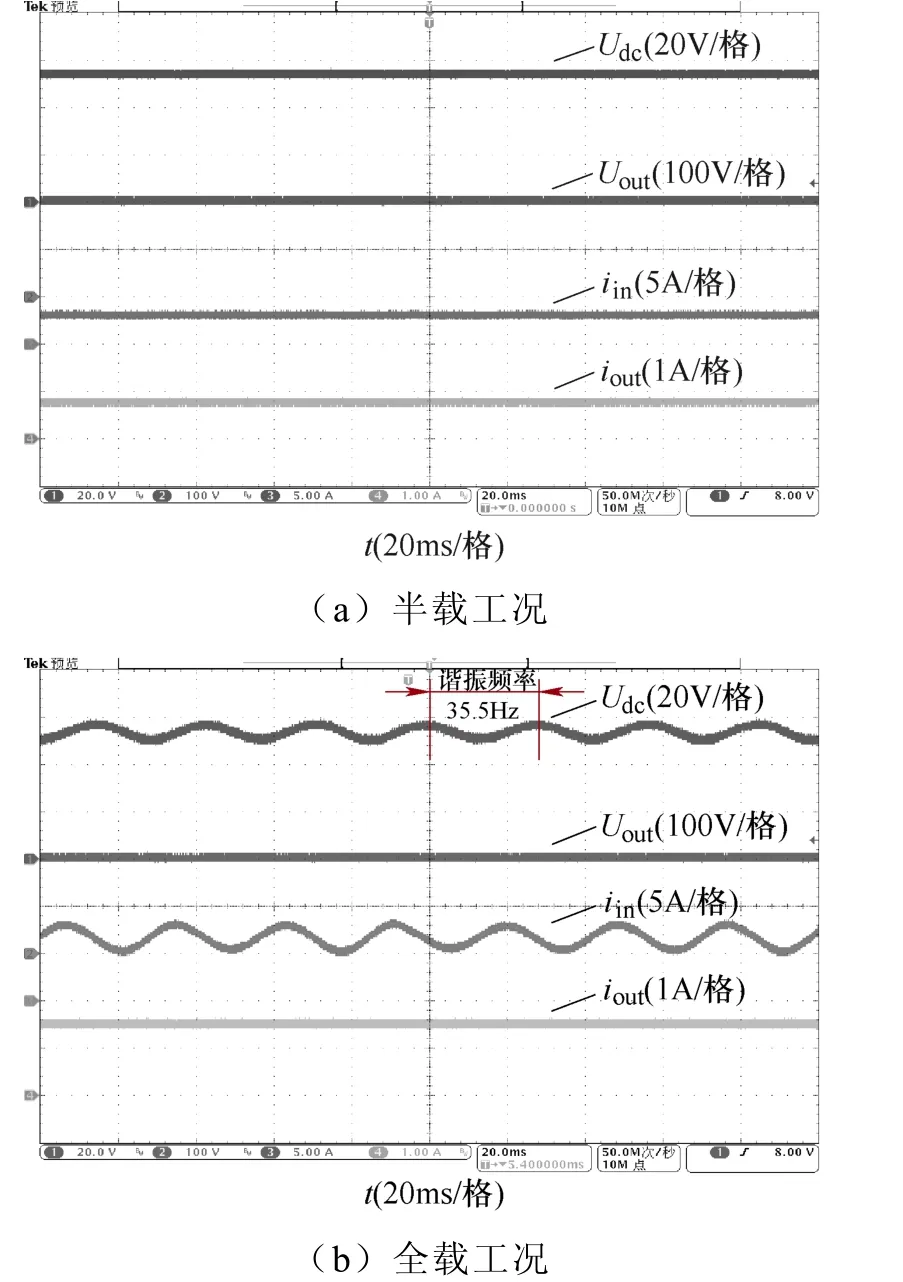
圖15 未采用PVI和SVI控制時，半載和全載工況下LC-DAB級聯系統電壓電流實驗波形 Fig.15 Voltage and current experimental waveforms of LC-DAB cascaded system under half load and full load conditions without PVI and SVI control

由圖15a可知，當未采用PVI和SVI控制，LC-DAB級聯系統在半載工況下運行時，一次側電容電壓Udc、二次側電容電壓Uout及負載電流iout均保持恒定，并未出現振蕩不穩定現象。但是當運行在全載工況下時，Udc出現振蕩，且振蕩頻率約為35.5Hz，和理論分析LC諧振頻率fr=35.58Hz基本一致，系統出現振蕩不穩定現象。同前述對LC-DAB級聯系統的穩定性分析相對應，進一步驗證了理論分析的正確性。

4.2 PVI與SVI控制驗證

加入PVI或SVI控制前后LC-DAB級聯系統電壓電流實驗波形如圖16所示。輸入電壓Uin=55V時，LC-DAB級聯系統全載運行，當運行至t1時刻，加入PVI控制，電壓電流波形如圖16a所示。同理可得在相同運行工況下，當運行至t2時刻，加入SVI控制，電壓電流波形如圖16b所示。

圖16 加入PVI或SVI控制前后LC-DAB級聯 系統電壓電流實驗波形 Fig.16 Voltage and current experimental waveforms of LC-DAB cascaded system before and after adding PVI or SVI control

由圖16a可知，在t1時刻前未加入PVI控制時，LC-DAB系統中電壓Udc發生振蕩。在t1時刻加入PVI控制后，可看出電壓和電流的振蕩完全被抑制，LC-DAB系統的穩定性得到了改善；SVI控制加入前后的實驗波形如圖16b所示，可知加入SVI控制后，電壓電流振蕩消失，系統逐漸調節至穩定狀態。由此驗證了本文所提PVI和SVI控制策略的有效性。

全載運行條件下，典型DAB變換器與采用PVI和SVI控制的LC-DAB級聯系統的電壓電流波形如圖17所示，其中，iinacr為輸入電流iin的交流分量。

典型DAB變換器的電壓電流實驗波形如圖17a所示，可知，DAB變換器電壓電流基本保持穩定，但其輸入電流存在較大的波動，電流峰峰值為1.50A，其方均根值為266mA。當運行在加入PVI控制的LC-DAB級聯系統時，可知系統電壓電流同樣保持恒定不變，但是輸入電流波動明顯減小，電 流峰峰值為520mA，相比典型DAB變換器降低了65.33%，電流方均根值為53.1mA，較典型DAB變換器減小了80.04%。當運行在SVI控制時，DAB變換器輸入電流峰峰值為540mA，與典型DAB變換器相比減小64%，電流方均根值為56mA，較典型DAB變換器降低了78.94%。由以上分析可知，加入PVI或SVI控制的LC-DAB系統不但有效地減小了電流諧波進入前級電源和后級DAB變換器，同時增強了LC-DAB系統的抗干擾能力。

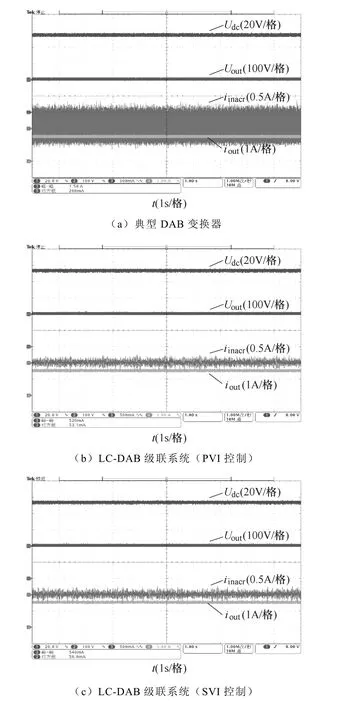
圖17 典型DAB與LC-DAB級聯系統的 電壓電流實驗波形 Fig.17 Voltage and current experimental waveforms of typical DAB and LC-DAB cascaded system

4.3 動態特性對比實驗

當負載功率由全載切換至半載運行一段時間后重新切換至全載。典型DAB變換器與LC-DAB級聯系統的電壓電流實驗波形如圖18所示。

圖18 負載變化時典型DAB變換器與LC-DAB級聯 系統的電壓電流實驗波形 Fig.18 Voltage and current experimental waveforms of typical DAB converter and LC-DAB cascaded system when load changes

由圖18可知，當負載功率變化時，加入PVI或SVI控制策略的LC-DAB系統電壓電流始終能夠保持穩定。并且當負載功率突降時典型DAB變換器的輸出電壓動態調節時間約為390ms，而在PVI控制下，LC-DAB系統輸出電壓調節時間約為350ms，較典型DAB變換器快40ms，同時在SVI控制下，調節時間為約375ms，較典型DAB變換器快15ms。當負載功率突增時典型DAB變換器的輸出電壓動態調節時間為490ms，而在PVI控制下時，調節時間約為370ms，較典型DAB變換器快120ms，在SVI控制下時，調節時間約為400ms，較典型DAB變換器快90ms。由此可得，加入PVI或SVI控制的LC-DAB系統不僅改善了輸入電流質量，而且縮短了輸出電壓的動態調節時間。

5 結論

本文通過對LC-DAB級聯系統小信號數學模型的推導，建立了阻抗模型并對其進行驗證。針對LC-DAB所出現的振蕩及穩定性問題，分別提出了PVI和SVI控制策略，理論分析和實驗結果表明：

1）PVI和SVI控制策略的加入，優化了DAB變換器的輸入阻抗，抑制LC-DAB級聯系統振蕩的同時增強了穩定性。

2）引入PVI和SVI控制能有效改善LC-DAB級聯系統的輸入電流質量，減小輸入電流的波動范圍，進而提高系統穩定裕度。