基于k-SC聚類的飛行操作模式及危險性分析

孫瑞山，李重鋒

(中國民航大學 安全科學與工程學院，天津 300300)

0 引言

2020年《中國民航航空安全報告》表明：2010—2019年的10 a間，我國民航由機組原因導致的飛行事故占到67.90%[1]，其中飛行員操作偏差是導致不安全事件發生的重要原因。快速存取記錄器(QAR)可全面記錄飛行員手動操作過程中產生的各類參數，包括飛行員操作參數，飛機性能參數與運行環境參數。飛行操作模式是指飛行員具有“代表性”的操作手法，基于QAR數據對其進行挖掘并建立其與不安全事件之間的映射關系，對于有針對性地提升飛行員操作能力、改善航司飛行訓練水平、保障飛機的運行安全等具有重要意義。

當前已有學者基于QAR數據對飛行員操作特征展開研究。首先是利用QAR截面數據對飛行員操作特性進行研究。例如，孫瑞山等[2]結合QAR數據及相關監控標準，確定了描述飛行員操作的完整性、平穩性、準確性和及時性的操作特征向量指標；董傳亭[3]利用功率譜密度方法獲得飛行操作的平穩性特征指標，進一步基于QAR數據構建出1套飛行操作評價體系；祁明亮等[4]以著陸階段的1類QAR超限事件為研究對象建立數學規劃模型，并針對該類事件的操作參數構成的“高風險子空間”進行分析。以上利用截面數據，即QAR數據的狀態值進行的研究忽略了數據的時序規律，特別是對于連續的飛行員操作而言，更需要從時間維度上挖掘相關數據的信息。針對這個問題，學者們將時間序列的相關算法應用于飛行員操作的相關研究中。例如，汪磊等[5]選取無線電高度、駕駛桿位以及油門桿位作為評價飛行著陸操作的關鍵指標，構建基于曲線相似度的飛行著陸操作評價模型；鄭磊等[6]使用基于分段線性表示和動態時間規整(DTW)的系統聚類方法挖掘QAR數據中蘊含的飛行操作模式，并在此基礎上利用卷積神經網絡模型構建精度較高的重著陸預警模型[7]，結果表明在已知飛行操作模式的前提下構建重著陸預警模型的召回率更高。

挖掘飛行數據中飛行操作特征的研究相對較少，如Wang等[8-9]基于QAR數據應用統計建模的方法對著陸階段的事件及操作風險進行分析，指出拉平操作對著陸績效的重要性；Matthews等[10]基于飛行品質監控數據提出1種新的多元時間序列搜索算法，用于識別包括人為因素在內的各類因素導致的重大運行事件；Kraemer等[11]基于飛行模擬器數據利用統計和聚類分析飛行員在正常、發動機故障和襟翼故障3種情況下的起飛操作并得出差異化結果。總體來說，當前基于飛行數據的研究更多注重飛行品質監控和異常檢測，對于飛行數據中飛行員操作特征的挖掘相對較少。

綜上所述，本文引入k-SC聚類算法挖掘QAR數據中蘊含的飛行員操作特征，該算法基于時間序列形狀相似度的度量完成飛行員操作數據的時間序列的聚類，比傳統的基于歐式距離的算法優越，同時比基于動態時間規整的算法更高效[12]。同時，結合不安全事件對k-SC聚類結果所反映的飛行操作模式的危險性進行分析，從而合理量化飛行操作模式的危險性，以期為和飛行員操作特征相關的研究提供理論參考。

1 時間序列相關理論

1.1 時間序列相似度不變性

分析時間序列的相似度是時間序列聚類的基礎，一般采用能識別其多種變化的距離度量方式來衡量[13]。即距離度量方式應滿足：

1)尺度變化：時間序列在尺度(縮放)中存在差異。如序列X變換為Y=aX+b，其中a和b為常數，X與Y的相似度不變；

2)位移變化：2個時間序列相位具有一定偏差，如Y(t)=X(t-t0)，X與Y的相似度不變；

3)噪聲變化：當2個時間序列具有相似的形態，但受到不同程度噪聲干擾時，2者相似度不變。

1.2 常用時間序列距離度量方法

在進行時間序列數據聚類時，常采用以下2種方法來進行相似度計算。

1)歐氏距離：對于同為n維的時間序列X=[x1,…,xn]和Y=[y1,…,yn]，2者的歐氏距離ED(X,Y)如式(1)所示：

(1)

式中：X與Y為時間序列；n為X的維度；ED(X,Y)為X與Y的歐式距離；xi和yi分別為X與Y中某時刻的值。歐氏距離在衡量時間序列相似性時對噪聲和異常點較敏感[14]，因此該方法雖然簡單高效卻很難精確度量時間序列之間的相似性。

2)DTW距離：處理時間序列分類時，序列長度可能不同，同時序列之間可能存在局部的扭曲。DTW允許時間序列彎曲時間軸，靈活地對時間序列進行匹配，實現局部范圍內匹配最優。對于n維X=[x1,…,xn]和m維Y=[y1,…,ym]，可利用動態規整方法尋找到規整成本最小的路徑，獲得最小動態時間彎曲距離，如式(2)所示：

DTW(X,Y)=τ(n,m)

(2)

式中：DTW(X,Y)為X與Y的DTW距離；τ(n,m)為累計距離；m為Y的維度。

k-SC聚類算法基于形狀相似性度量處理時間序列在尺度和位移上的扭曲，滿足尺度與位移不變性且計算效率高；對比基于ED度量時間序列相似性的k-means聚類算法，k-SC算法具有更高的分類準確性[12]。因此，k-SC聚類算法適用于挖掘海量QAR數據中蘊含的飛行操作模式。

2 飛行操作模式挖掘及危險性分析方法

2.1 問題定義

飛行過程中，飛行員主要通過對桿、油門、舵等的操縱實現對飛機高度、速度、姿態等的控制。QAR可記錄飛行操作數據(如桿位、油門位參數等)隨時間變化的情況，即操作參數i對應1個長度為n的時間序列Xi=[xi1,…,xin]。通過分析飛行員的QAR時間序列數據，可以發現飛行員控制駕駛桿、油門桿、升降舵等的時機和變化情況，進而與規章、手冊的要求或建議進行對比并發現問題；對于飛行員操作中存在的共性特征，即本文定義的飛行操作模式，如“抬頭慢”、“拉平早”等還需要進一步對重點安全監控參數，如飛機的著陸垂直載荷、15.24 m至接地平飄距離等進行分析并量化飛行操作模式的危險性，進而有針對性地排除飛行員的操作隱患。

綜上所述，本文主要研究2方面問題：

1)飛行操作參數的時間序列聚類，即從某一參數的時序數據中挖掘相似的飛行操作模式。

2)分析飛行操作模式與QAR監控事件之間的關聯關系，量化不同飛行操作模式的危險性。

2.2 飛行操作模式分析

針對問題的定義，飛行操作模式的挖掘可轉化為對飛行操作參數序列的相似性研究。k-SC聚類基于某飛行操作參數序列的相似性分析完成聚類。

具體地，對于某操作參數序列集合C的任意2個序列X=[x1,…,xn],Y=[y1,…,yn]，k-SC聚類算法的序列相似度度量方法如式(3)所示：

(3)

該方法找到最優平移q和比例系數α來匹配2個時間序列的形狀。具體為，首先找到q′使X,Y在同一時間達到峰值，然后在q′周圍尋找最優q。固定q后，式(3)是1個關于α的凸問題，通過設置梯度為0計算出α最優值如式(4)所示：

(4)

式中：α*為α的最優值。

在飛行操作參數序列的相似性度量基礎上進行k-SC聚類，定義方程F如式(5)所示：

(5)

式中：F為度量聚類效果評價值，F越小，k-SC聚類效果越好；K為聚類數；Xi為某個類中的時間序列；Ck為第k類的序列集合；μk為第k類的聚類中心。

問題轉化為尋找最優聚類中心使得F最小，如式(6)所示：

(6)

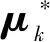
由式(3)與式(6)得式(7)：

(7)

式中：αi和qi為對Xi的比例系數和平移量。

考慮(不失一般性)Xi已經被qi移位并將α*代入式(7)，結果如式(8)所示：

(8)

式(8)化簡后如式(9)所示：

(9)

此外，采取經典的肘部法則來確定最佳聚類數[16]。不同K值對應不同的F，隨著聚類數K值的增加，每類樣本數的減少，樣本距其聚類中心的距離減小，平均畸變程度降低。K值增大過程中，F值下降幅度最大的位置對應的K′值就是肘部，K′即為最佳聚類數。根據k-SC聚類的特點對肘部法則進行改進，采用改進的誤差平方和(SSE)確定，結合式(3)得出改進的SSE計算方法如式(10)所示：

(10)

式中：SSE′為改進的誤差平方和。

設定初始聚類數Kmin和最大聚類數Kmax后，具體的飛行操作模式聚類流程如圖1所示。

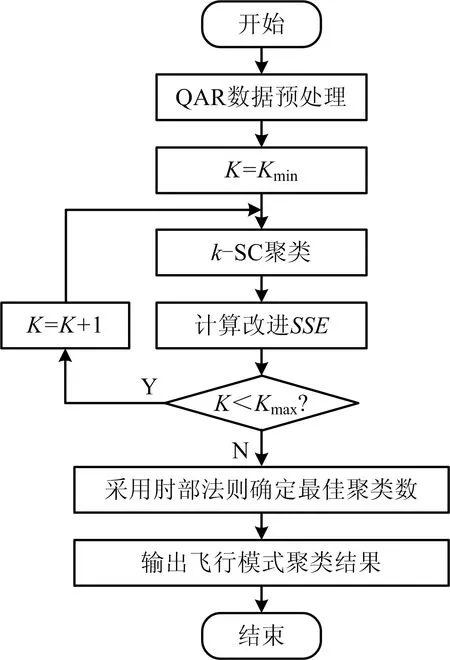
圖1 飛行操作模式挖掘流程Fig.1 Flow chart of flight operation patterns mining

2.3 飛行操作模式危險性分析

以QAR不安全事件的監控標準作為飛行操作模式危險性高低的判斷依據，采用Kruskal-Wallis檢驗(K-W檢驗)，對飛行操作模式聚類結果監控參數分布的差異性進行檢驗[17]，進一步做出危險性評判。K-W檢驗是1種推廣的多獨立樣本平均秩檢驗，屬于非參數檢驗。K-W檢驗的原假設H0為：樣本來自的多個獨立總體的分布無顯著差異。

基于K-W檢驗的飛行操作模式危險性分析步驟為：

1)確定機隊飛行操作模式危險性分析的不安全事件及對應的監控參數和監控標準。

2)依照k-SC飛行操作模式聚類結果對數據進行分組并對各組不安全事件發生的占比進行統計，選取平均水平作為劃分危險性高低的依據。

3)針對所選取的不安全事件監控參數對各組聚類結果進行K-W檢驗。

4)基于K-W檢驗結果和各組不安全事件占比分析飛行操作模式的危險性。

3 案例分析

3.1 數據處理

根據波音公司2009至2018年的統計數據[18]，著陸階段雖然在時間上只占整個航程的1%左右，但發生的重大事故占全部航段重大事故的24%左右；波音公司的機組訓練手冊表明，在著陸階段飛行員需要操縱駕駛桿完成正常的運動軌跡、速度和正確的配平操作，并在主起落架高于跑道約6 m時操縱駕駛桿逐漸增加俯仰姿態約2°～3°開始拉平，以減緩飛機的下降率；同時，相關學者基于QAR數據應用統計建模的方法對著陸階段的事件及操作風險進行分析，指出飛行員對駕駛桿的操作，特別是對拉平環節的操作影響著飛機的著陸績效[8-9]。綜上所述，本文采集某機隊飛機著陸接地前20 s的飛行參數數據，并以駕駛桿操作的時間序列為例進行研究。

由于機場條件、氣象條件等外部因素均會影響到飛行操作，不同機場海拔、跑道條件等環境因素下的飛行操作要求不盡相同，因此，本文依據以下條件對數據進行篩選：落地機場固定；特定機型；著陸重量小于60 000 kg；飛機著陸形態為襟翼30°；機場溫度30～35 ℃；頂風風量小于10 m/s，順風分量小于5 m/s的樣本記錄進行分析。最終，共收集422次QAR數據記錄并利用Python進行批量化預處理，包括采用極值歸一化將序列數據壓縮在區間[0,1]之間。

3.2 駕駛桿操作模式分析

為說明實驗方法的可行性，選取Kmin為2，Kmax為10。利用式(10)計算不同聚類數K對應的SSE′值，其對應關系如圖2所示。

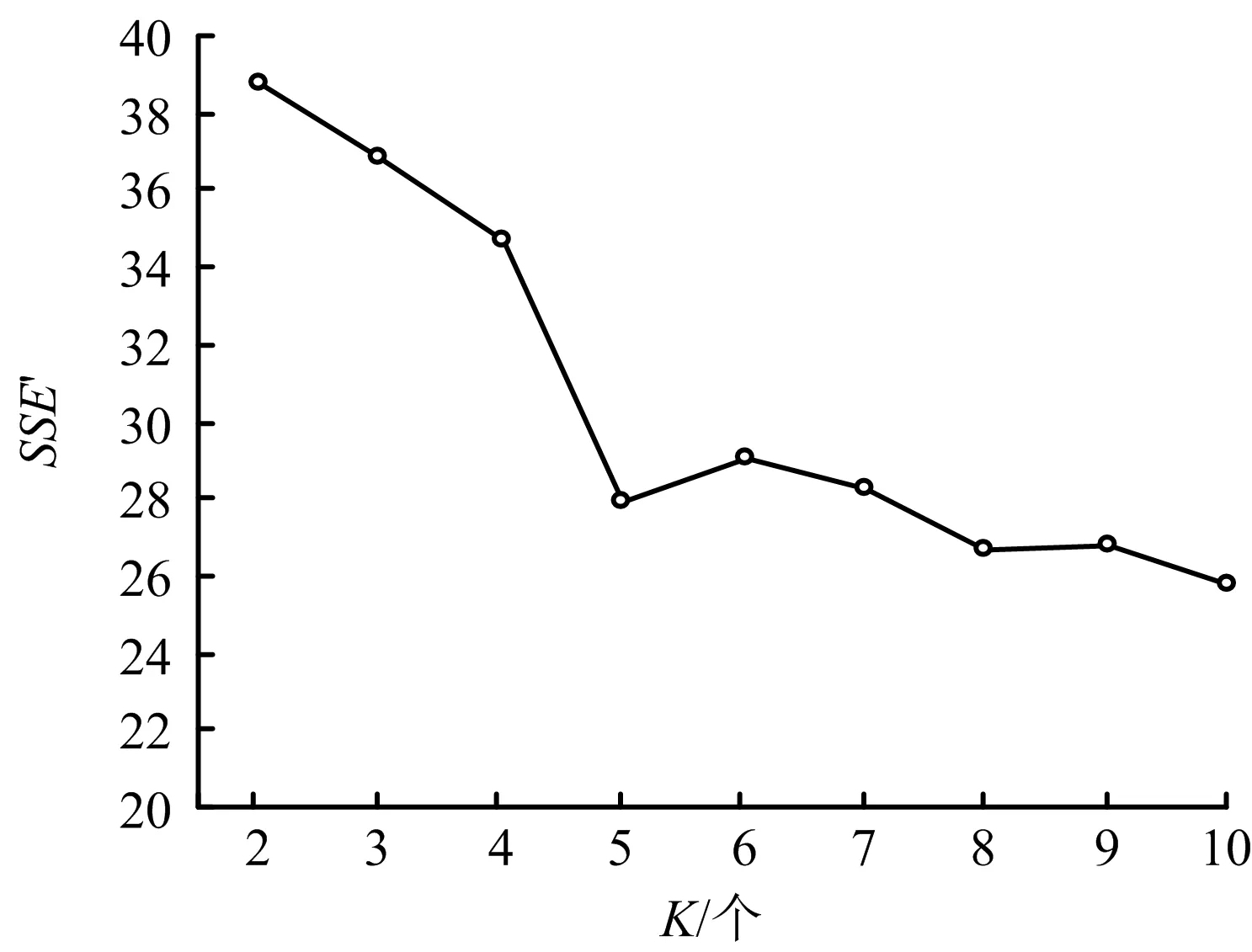
圖2 K與SSE′之間的關系Fig.2 Relationship between K and SSE′

可以看出SSE′在K=5處變化最大，選取最佳聚類數為5。在此基礎上由式(10)得出最終的著陸前20 s駕駛桿位時間序列的各個聚類中心如圖3所示。

圖3中，橫坐標起始時間為飛機著陸前20 s的第1 s。

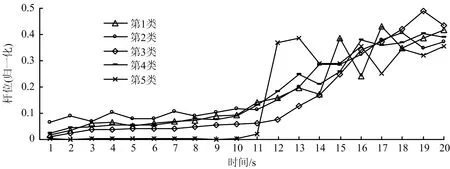
圖3 k-SC聚類結果Fig.3 Results of k-SC clustering

圖3所示的5類操作模式中，第1類表示飛行員在第10 s左右開始拉桿，在出現2次幅度較大的推拉桿動作后小幅拉桿接地；第2類表示飛行員初始操作較不穩定，在第11 s左右拉桿，在第18 s左右出現持續1 s左右的小幅推桿后繼續拉桿并接地；第3類表示飛行員在第11 s左右開始拉桿，在第19 s左右推桿接地；第4類表示飛行員在第10 s左右拉桿，做出3次小幅推拉桿動作后推桿接地；第5類表示飛行員在第11 s左右大幅拉桿，做出2次幅度較大的推拉桿動作后拉桿接地。

可以看出，5類操作模式對應駕駛桿位時間序列的形狀存在一定差異，主要體現在初始拉桿時機、拉桿幅度及拉平穩定性等的控制上。

3.3 駕駛桿操作模式危險性分析

為進一步分析不同操作模式的危險性，選取長著陸事件為分析目標。長著陸是1種著陸不安全事件，會降低跑道的使用效率，增加飛機沖出跑道的概率[19]。長著陸對應飛行品質監控項目為15.24 m至接地距離遠，監控參數為15.24 m至接地段的地速積分距離D，具體的監控標準參考波音飛行品質監控輕度超限取值為750 m。按照k-SC聚類結果將D分為5組進行K-W檢驗，并設檢驗顯著性水平α為0.01，K-W檢驗結果如表1所示。

表1 K-W檢驗結果Table 1 Results of K-W test

K-W檢驗結果表明，不同駕駛桿操作模式的地速積分距離D的分布不同，第1類操作模式的秩平均值最高，第3類操作模式的秩平均值最低。將各組對應長著陸事件數的占比與平均占比水平(55.68%)對比得出高危險性操作模式為第1類和第4類，第4類駕駛桿操作模式對應發生長著陸的危險性最高。

總體來看，特定條件下該機隊飛行員的5類駕駛桿操作模式起始拉平時間近似相同，其中長著陸危險性較高的駕駛桿操作模式具有推拉桿次數較多的特點，即拉平至接地段對駕駛桿操作平穩性較差。對比危險性較低的操作模式，可以看出平穩連續地拉桿可以降低飛機的平飄著陸距離，從而減小飛機發生長著陸的危險性。因此，航空公司可從以上角度對機隊現存的長著陸危險性較高的飛行操作模式進行改進訓練，以持續提升機隊安全運行水平。

4 結論

1)基于k-SC時間序列聚類及K-W檢驗給出高危險性飛行操作模式的挖掘方法；結合實際QAR數據進行方法驗證，得出2類長著陸危險性較高的駕駛桿操作模式。

2)方法可輔助提升航空公司飛行員的操作水平，同時可以拓展應用至其他飛行不安全事件模型的研究，如重著陸等，以期結合飛行操作模式為相關研究的進一步開展提供依據。

3)暫未考慮復雜天氣、不同機場或不同機型對飛行員操作模式的影響，同時由于案例樣本量的限制，操作模式挖掘過程中最高聚類數的取值較小，未來可考慮使用大數據方法挖掘更多復雜條件下的高危險性飛行操作模式。