基于樹莓派的單像素成像系統

何自豪，韓佳成，王琳淼，趙天賜，張素恒

(河北大學 物理科學與技術學院，河北 保定 071002)

近年來，單像素成像技術作為一種新型成像技術引起廣泛關注.單像素成像與傳統的陣列探測器成像相比，其圖像信息的獲取方式與采集效率不同，在硬件復雜度和工業成本方面占有一定優勢，對于推動未來成像系統的簡化和集成，具有潛在應用前景.現階段，陣列傳感器件在紅外、太赫茲波段的應用并不成熟，并且三維成像、光譜成像對器件的分辨率和靈敏度要求苛刻，其應用受到限制，因此單像素成像技術的出現，為解決這些問題帶來了新的途徑.

單像素成像發展至今，先后經歷了計算鬼成像、基于壓縮感知的單像素成像和基掃描單像素成像3個階段[1].基掃描單像素成像是使用確定性的正交變換基底圖案進行空間光調制的成像方法.通過采用完備的基底圖案進行空間光調制，可以無失真地重構物體的像，這是該成像方法的顯著優勢.2015年，李明飛等人提出了基于沃爾什-哈達瑪變換的單像素成像方案[2]，之后他們又研究了矩陣優化排序的壓縮采樣快速成像方案[3].2016年，張子邦等人引入了傅里葉單像素成像技術[4-6].此外，他還對比了傅里葉單像素成像與哈達瑪單像素成像在欠采樣情況下的成像質量[7].2016年，Liu Bao-Lei等人提出基于離散余弦變換的單像素成像方案[8].2017年，Rousset L等人又提出基于小波預測的自適應基掃描單像素成像方案[9].這些基掃描成像方案極大的推動了單像素成像技術實用化進程.

雖然國內外在單像素成像領域已經開展了大量的研究工作，提出多種成像系統.但這些單像素成像系統集成度較高，可操作性差，價格昂貴，不利于在實驗教學中推廣.本文提出了一種基于樹莓派的單像素成像系統.該系統以基掃描單像素成像技術為基礎，以樹莓派為核心，并采用Python語言進行軟件開發，結構簡單，成本低廉，可操作性強，非常適合實驗教學.本文首先介紹基掃描單像素成像的原理，然后分別從硬件和軟件兩個方面詳細介紹系統結構，最后展示哈達瑪和傅里葉兩種基掃描單像素成像實驗結果.

1 基掃描單像素成像原理

基掃描單像素成像依次向物體投影一套完備的正交變換基底圖案，并逐一測量每一基底圖案照明時物體的漫反射光強，從而獲取物體的各個頻譜分量，再通過逆變換重建物體的像.

1.1 哈達瑪單像素成像

二維的哈達瑪變換與其逆變換定義為

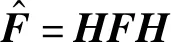
(1)

(2)

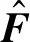
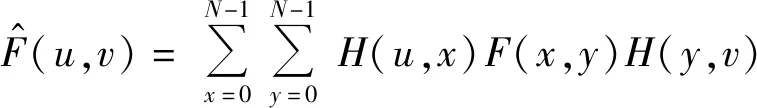
(3)

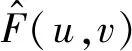
{Puv|u,v=0,1,…,N-1}

(4)

其中基底矩陣Puv的矩陣元為

Puv(x,y)=H(u,x)H(y,v)

(5)

其中x,y=0,1,…,N-1.若將哈達瑪矩陣H的第u行和v行的行向量分別為記為Hu與Hv，則由式(5)可知，基底矩陣Puv還可表示為

(6)

考慮到哈達瑪矩陣HT=H.這時式(3)可表示為

(7)

其中〈·,·〉F代表Frobenius內積.由式(7)可知，只要逐一計算物體采樣矩陣與基底矩陣序列中每一基底矩陣的內積，即可得到物體的哈達瑪頻譜.

在單像成像中，首先根據基底矩陣序列生成基底圖案序列，然后再將所有基底圖案逐一投影到物體上形成結構光照明，最后利用單像素測探器記錄物體的漫反射光強，即可獲取物體完備的頻譜.由于結構光照明是對光強調制，無法直接表達哈達瑪基底矩陣中的負值.通常采用差分法來解決該問題.于是將每個基底矩陣Puv轉化為兩幅基底圖案

(8)

然后把這兩幅基底圖案依次投影到物體上，單像素探測器測得的漫反射物光強分別為

(9)

其中I0為投影光源的強度，Ib為不受調制的背景光強度分布矩陣，k是探測器的光電響應系數.通過差分即可得到相應的哈達瑪頻譜分量，

(10)

其中α=1/kI0.此外，差分還能去除背景光影響.

在成像過程中，依次向物體投影整套基底圖案

(11)

測得漫反射物光強序列為

{D(+)(u,v),D(-)(u,v)|u,v=0,1,…,N-1}

(12)

從而得到物體的哈達瑪頻譜矩陣，

(13)

最后再利用式(2)對頻譜矩陣進行逆變換即可獲取物體的重構像.

圖1 差分哈達瑪單像素成像基底圖案(4×4像素)

哈達瑪單像素成像的空間采樣間隔由投影到物體上的基底圖案的最小結構單元的尺寸來決定.通過最近鄰域法放大基底圖案和調整投影距離均可改變空間采樣間隔，以獲得最佳的成像效果.

1.2 傅里葉單像素成像

二維離散傅里葉變換定義為

(14)

其中u=0,1,…,M-1;v=0,1,…,N-1，M與N分別為物體采樣矩陣F的行列數.二維離散傅里葉逆變換定義為

(15)

其中x=0,1,…,M-1;y=0,1,…N-1.考慮到離散傅里葉變換的周期性，引入離散傅里葉變換基底矩陣序列

(16)

其中基底矩陣Tuv的矩陣陣元為

(17)

其中

(18)

其中?·」與「·?分別代表向下取整運算與向上取整運算.二維離散傅里葉變換式(14)可表示為

(19)

由式(19)可知，物體的離散傅里葉頻譜可通過計算物體采樣矩陣與基底矩陣序列所有基底矩陣的內積獲得.

由式(17)可知，離散傅里葉變換基底矩陣為復矩陣.為了通過光強調制表達該基底矩陣，通常借助于四步相移法.首先將基底矩陣序列中的每個基底矩陣Tuv經相移后轉化為四幅余弦基底圖案

(20)

其中Re{·}代表取實部.然后把這四幅基底圖案依次投影到物體上，單像素探測器測出的漫反射物光強分別為

(21)

由歐拉公式可計算出相應的頻譜分量

i[D(π/2)(u,v)-D(3π/2)(u,v)]}

(22)

可以看出，四步相移法的本質仍為差分運算，同樣可以消除背景光的影響.

在基于傅里葉變換的單像素成像過程中，依次向物體投影整套余弦基底圖案

(23)

測得漫反射物光強度序列為

(24)

從而得到物體的離散傅里葉頻譜矩陣

(25)

然后再對頻譜矩陣進行逆變換，則有

(26)

式中ifft代表二維離散傅里葉逆變換.但這時得到的重構像Fc中心位于矩陣左上角，不便觀察.考慮到離散傅里葉變換的周期性，通過fftshift操作對重構像進行調整，即

F=fftshift(Fc)

(27)

最終獲得物體的重構像.

圖2 四步相移傅里葉單像素成像基底圖案(4×4像素)

考慮到物體的分布函數(物體光強反射率)為實值函數，物體采樣矩陣的傅里葉頻譜滿足共軛對稱性，即

(28)

因此，可以僅測量頻譜中的零頻及負頻分量，再用式(28)補全正頻分量，從而獲得完整的頻譜[6].這時測量次數可減少一半.當物體的細節不太豐富時，還可以進行欠采樣成像，進一步減少測量次數，加快成像速度，詳見參考文獻[7].

當u與v均取最大值時，即

|um|=?M/2」,|vm|=?N/2」

(29)

余弦基底圖案空間頻率最高.投影到物體上的該余弦條紋沿x方向與y方向空間周期的一半即為傅里葉單像素成像的空間采樣間隔.對式(18)中離散坐標序列進行線性取值，可以放大基底圖案，進而改變成像的空間采樣間隔.此外，還可以通過調整投影距離改變成像的空間采樣間隔.

2 基于樹莓派的單像素成像系統設計

樹莓派是為普及計算機編程教育而設計的基于ARM架構的微型電腦，其體積小、價格低、接口豐富、性能強大.樹莓派的操作系統Raspberry Pi OS基于Linux完全開源，功能完備，并且預置了Python的開發環鏡.因此，它非常適合編程學習和創客開發.本文提出在實驗教學中利用樹莓派代替傳統計算機搭建單像素成像系統，非常有利于鍛煉學生的動手能力，培養其創新思維.

2.1 硬件設計

硬件系統如圖3所示，主要由3部分組成：控制單元、圖像投影單元和數據采集單元.系統的核心是控制單元，由樹莓派(4B)構成.控制單元主要負責生成基底圖案，控制投影和數據采集，進行數據處理與計算重構圖像.圖像投影單元由米家激光投影儀(L185JCN)構成，通過HDMI接口與樹莓派連接.投影單元將樹莓派發送來的基底圖案投影到物體上.數據采集單元由光強傳感器(OPT101)，濾波模塊與數據采集卡(MCC-118)3個部分構成.光強傳感器將基底圖案照明下的漫反射物光強度轉換為電壓信號輸送給濾波模塊.濾波模塊是由RC濾波電路構成的低通濾波器，它可將光電轉換過程中產生的大量噪聲去除.經濾波后的電壓信號送給數據采集卡，由采集卡進行模數轉換.數據采集卡通過GPIO接口與樹莓派連接，它在樹莓派的控制下進行數據采集，并將采集到的光強數據回傳給樹莓派.

圖3 硬件系統框圖

整個系統成本較低，其中樹莓派(4B)380元，數采卡(MCC-118)990元，光強傳感器(OPT101)4元，米家激光投影儀(L185JCN)5000元，合計6374元.在演示實驗中，可采用多媒體教室的投影儀[11]總成本可降至1500元以內.

2.2 程序設計

單像素成像系統程序采用Python語言開發，它簡潔、易讀，并且具有強大的擴展能力.程序主要完成基底圖案生成與顯示，數據采集，圖像重構等操作，程序流程如圖4所示.

圖4 程序流程框圖

程序開始運行后，首先執行初始化操作，包括導入科學計算庫、數據采集庫與圖像顯示庫，實例化采集卡并設定采集參數，初始化顯示模塊并設定顯示參數.然后構建一個生成器(generator)用于迭代生成全部基底圖案，以避免大量的內存消耗.接下來迭代顯示每一張基底圖案，在循環過程中，每顯示一張基底圖案，先延時100 ms，待圖像顯示穩定后，再進行數據采集.對于每幅基底圖案，將以10-4s的采樣速率，采集400個樣本，再對這400個樣本求平均，作為該幅基底圖案照明時的漫反射物光強度.當循環顯示全部基底圖案后，計算重構圖像，并將重構圖像保存并顯示在屏幕上.

3 實驗驗證

按照上述的系統設計方案，開發了如圖5所示的實驗裝置，來驗證設計方案的可行性.實驗中，將河北大學校名與校徽制作成剪紙置于黑色幕布上作為物體，如圖6所示.兩物體大小相同，長寬均為0.6 m.實驗采用哈達瑪與傅里葉兩種基掃描單像素成像方式分別對這兩個物體成像.

圖5 實驗裝置圖

圖6 待成像物體，物體的長與寬均為0.6 m

在對河北大學校名進行成像時，取像的分辨率為128×128像素.采用哈達瑪單像素成像時，直接生成的哈達瑪基底圖案大小僅為128×128像素.為了便于投影，首先按最近鄰域法將圖像放大到1024×1024像素，再加載到投影儀上顯示.然后調整投影儀與物體的距離，使幕布上的基底圖案剛好完整覆蓋物體.投影儀逐一投影全部128×128×2張基底圖案，利用式(13)對測量數據進行差分處理即可得到物體的哈達瑪頻譜，如圖7(a)所示.

對測得的哈達瑪頻譜矩陣再按式(2)進行逆變換，即重構出物體的像，如圖8(a)所示.在傅里葉單像素成像時，取式(18)中的M=N=128，先對離散坐標序列x和y進行插值，使坐標點數增加至1024，再按照式(17)計算出傅里葉基底矩陣，再生成全部128×128×4張基底圖案進行投影顯示.利用式(22)對測量數據進行處理即可得到物體的傅里葉頻譜，如圖7(b)所示.為清楚顯示譜頻分布，該圖為原頻譜進行對數變換后的結果.物體的傅里葉頻譜矩陣再經過式(26)與式(27)變換后最終得到物體的重構圖像，如圖8(b)所示.從圖8可以看出，在該分辨率下，在兩種成像方式均可獲取高質量的像，字樣的細節清晰，對比度也比較高.

圖8 河北大學校名的成像結果，分辨率為128×128像素

當對河北大學校徽成像時，取分辨率為256×256像素，成像結果如圖9所示.這時兩種成像方式均可完整呈現物體豐富的細節，但成像的對比度有不同程度的下降.對比圖8與圖9兩組實驗結果可以看出，哈達瑪變換成像質量明顯優于傅里葉變換的成像質量.這是因為傅里葉基底矩陣連續取值，在生成數字化的基底圖案過程中會引入量化誤差，在投影儀投影該灰度圖像時又會引入非線性誤差.而哈達瑪基底矩陣是二值矩陣，不會受上述噪聲的影響，因而哈達瑪單像素成像具有較高的成像質量.

圖9 河北大學校徽成像結果，分辨率為256×256像素

最后需要指出的是，上述所有成像結果，均未進行任何后期處理.若根據系統噪聲特性與物體特征對像進行降噪增強處理，則成像質量將會進一步提升.

這兩組實驗結果表明，本文提出的基于樹莓派的單像素成像方案合理可行，能夠對物體高質量成像.

4 結論

以基掃描單像素成像為基礎，本文設計并開發了一套基于樹莓派的單像素成像系統.利用該系統成功實現哈達瑪單像素成像與傅里葉單像素成像，驗證了設計方案的可行性.系統硬件結構緊湊，成本低廉，易于推廣；系統程序由Python語言開發，清晰簡潔，易于拓展.因此，該系統非常適用于單像素成像的原理演示與實驗教學.另外，本工作還能推動單像素成像技術走出科研實驗室，向小型化、實用化發展.