基于改進的鯨魚優化算法的物流車輛配送路徑規劃

唐 彥，張進軍

(安徽警官職業學院，安徽 合肥 230001)

帶容量約束的車輛路徑問題(Capacitated Vehicle Routing Problem，CVRP)的主要特征是車輛有最大容量限制、各客戶需求點有貨物配送需求，該問題是一種典型的NP-Hard組合優化問題[1]。傳統算法很難求解CVRP問題，近年來很多研究人員將群智能算法應用于CVRP問題求解。文獻2將混合變鄰域生物共棲搜索算法應用于CVRP問題求解[2]。文獻3將多種群人工蜂群算法用來求解帶重新路由策略的CVRP問題[3]。文獻4提出了一種基于改進的粒子群優化算法的車輛路徑優化方法[4]。

鯨魚優化算法[5](Whale Optimization Algorithm，WOA)具有控制參數少、收斂速度快和計算簡單等優點，是一種模仿座頭鯨捕食行為而衍生出的新型群體智能搜索算法。該算法已在機器學習、函數尋優、數據挖掘、電力調度、控制器設計調優等方面得到廣泛應用[6-7]。目前應用鯨魚優化算法求解CVRP的文獻較少，因此本文提出一種基于改進的鯨魚優化算法的物流配送車輛路徑優化方法。研究結果表明，與WOA、PSO和GA相比，改進鯨魚優化算法可以有效降低物流配送成本和減少配送距離，為車輛路徑規劃提供了新的方法。

1 改進的WOA算法

在標準的WOA算法中，座頭鯨包括包圍獵物、狩獵行為和隨機搜索獵物等3種行為，每一只座頭鯨的位置為一個可行解。

1.1 包圍獵物

座頭鯨發現獵物后能夠快速包圍式(1)所示的所發現的獵物并更新位置：

(1)

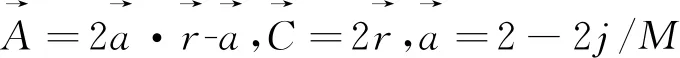
(2)

式(2)中，M為最大迭代次數；a和r為隨機數，a∈[2,0]，r∈[0,1]。

1.2 狩獵行為

座頭鯨狩獵采用如式(3)所示的螺旋運動方式：

(3)

式(3)中，l∈[-1,1]的隨機數；b為螺旋形狀的常數。

在座頭鯨的狩獵行為中，鯨魚位置更新的過程中將以50%的概率包圍如式(4)所示的獵物或進行螺旋式狩獵：

(4)

1.3 隨機搜索獵物

當A>1或A<-1時，鯨魚群體離獵物遠去，隨機搜索更為合適的獵物，數學模型為式(5)所示：

D=|C·Xrand(t)-X|，X(t+1)=Xrand-A·D

(5)

式(5)中，Xrand為隨機選擇的鯨魚位置。

針對鯨魚算法容易陷入局部最優和“早熟”問題，將非線性收斂因子引入標準WOA算法，提出一種改進的鯨魚優化算法(Improved Whale Optimization Algorithm，IWOA)，其改進策略為：

收斂因子a數值大小直接影響WOA算法的搜索能力和尋優能力。在基本WOA算法中，收斂因子a搜索前期較大，后期較小，導致其后期容易陷入局部最優，本文為解決該問題，提出一種隨迭代次數非線性變化的收斂因子，其更新公式為式(6)：

(6)

式(6)中，astart和aend分別為a的初始值和終止值；μ為調節系數，文中取μ=25。

2 物流車輛配送路徑規劃

車輛配送路徑規劃問題可表述為[8-9]：假設配送中心配備有K輛物流運輸車，車輛載重容量為qk(k=1,2,3,…,K)，配送需求點有L個，第i個需求點的需求量為gi(max(gi)≤max(qi))，完成需求點任務i貨物裝載或卸貨的時間為Ti，其中任務i必須在時間段[ETi,LTi]內完成。ETi、LTi分別為任務i的最早開始時間和最遲開始時間。若配送車輛早于ETi到達需求點，則配送車輛等待；否則，任務將被延遲。車輛物流配送示意圖如圖1所示。

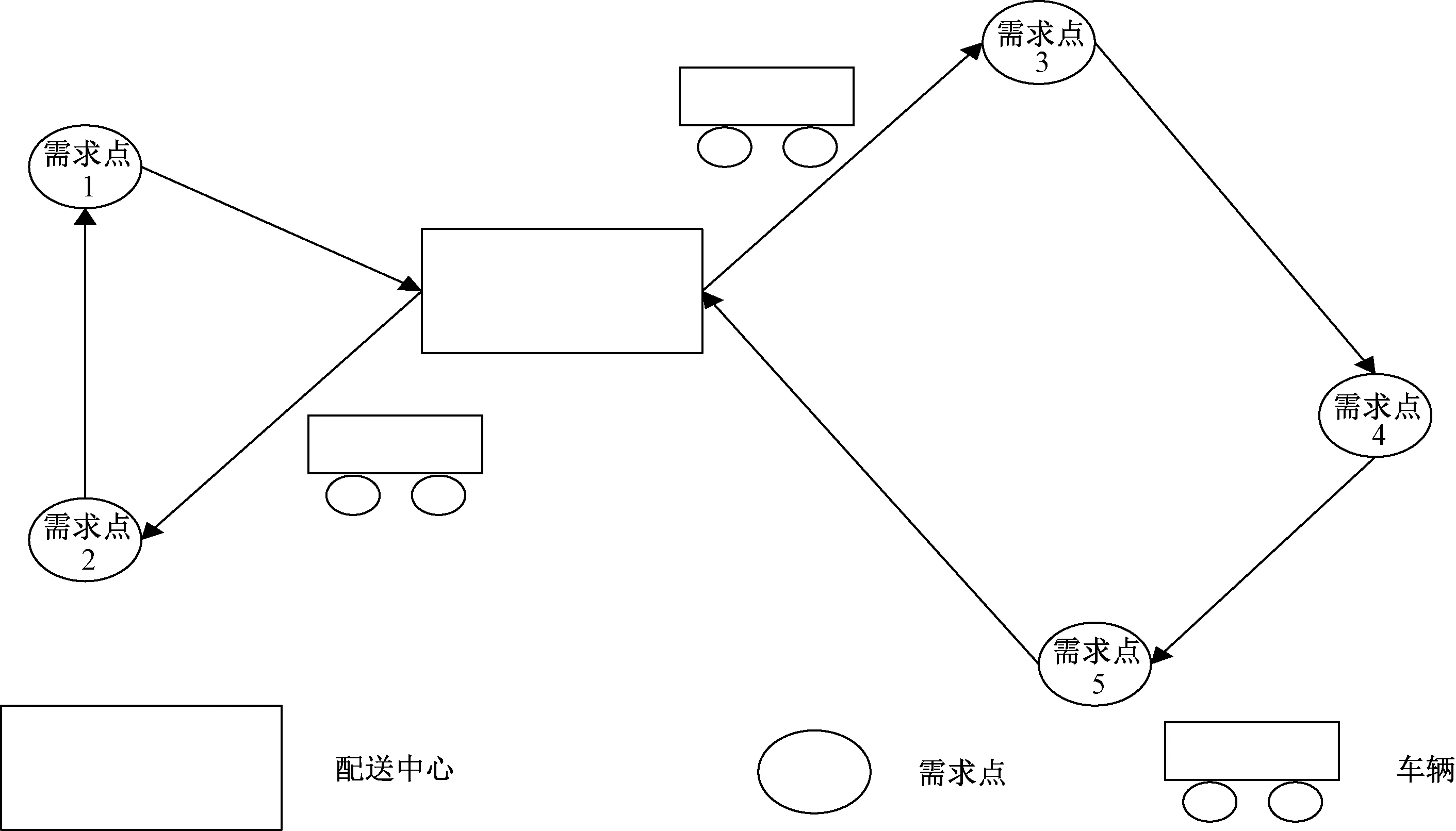
圖1 車輛物流配送示意圖

根據問題描述將貨物需求點編號為1,2,3，…,L，物流配送中心編號為0，任務和配送中心編號為i=(0,1,2,3,…L)，則決策變量為[10]：

(7)

(8)

綜合所述，物流車輛配送路徑數學規劃模型為：

(9)

(10)

(11)

(12)

式(9)～(12)中，si為配送車輛到達需求點i的時間；cij為需求點i到需求點j的運輸成本；pE、pL分別為配送車輛提前到達需求點i的或者滯后到達需求點i的單位時間內的等待成本以及懲罰成本。該數學模型中每個需求點均有車輛配送，且每個需求點只能由一輛物流配送車輛配送；與此同時，同一配送路徑上的需求點的需求量之和應小于等于物流配送車輛的最大載重。

為實現物流配送車輛路徑的最優規劃，解決該問題的關鍵是構造合適的最佳鯨魚位置表達方式。參考文獻11-12構造一個2L維空間對應L個需求點任務的物流配送車輛路徑規劃問題，保證需求點任務為2維[11-12]。若需求點任務為7，配送車輛為3，需求點任務編號為[1 2 3 4 5 6 7]。此時最佳鯨魚位置向量X如圖2所示，其中最佳鯨魚位置對應物流配送車輛的編號和行駛路徑。

圖2 車輛和路徑編號

由圖2車輛和路徑編號可知，最佳鯨魚位置對應的物流車輛配送路徑為：(1)車輛1∶0→1→0；(2)車輛2∶0→4→5→3→2→0；(3)車輛3∶0→7→6→0。

基于IWOA的車輛配送物流路徑優化算法步驟具體描述如下：

Step1：設定IWOA算法參數：種群規模N、最大迭代次數Maxgen、當前迭代次數t以及螺旋形狀常數b，并且隨機初始化鯨魚群體初始位置Xi(i=1,2,…,n)；

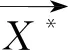
Step2：按式(13)計算每個鯨魚個體的適應度，并對適應度進行排序，找到適應度最小時所對應的鯨魚個體即最佳鯨魚個體X*并保存；

(13)

Step3：如果t≤Maxgen，則更新參數a、A、C、l和p；

Step4：當p<0.5時，如果|A|<1，按式(1)更新當前鯨魚個體的空間位置；當|A|≥1時，則隨機選擇鯨魚個體位置Xrand，并且按式(5)更新當前鯨魚個體的空間位置；

Step5：當p≥0.5時，按式(4)更新當前鯨魚個體的空間位置；

Step6：限制和修正鯨魚個體搜索空間；

Step7：按式(13)計算每個鯨魚個體的適應度，并對適應度進行排序，找到適應度最小時所對應的鯨魚個體即最佳鯨魚個體X*并保存；

Step8：判斷算法終止條件：如果t≥Maxgen，則轉到步驟Step9；反之，重復步驟Step3～Step7；

Step9：輸出最優鯨魚個體的空間位置X*及其適應度，即輸出車輛物流配送路徑。

3 仿真試驗與結果分析

為了驗證IWOA進行物流配送車輛路徑規劃的有效性和可靠性，選擇參考文獻13中實例為研究對象[13]，各需求點的坐標位置以及用戶需求和中心倉庫數據信息如表1和表2所示。

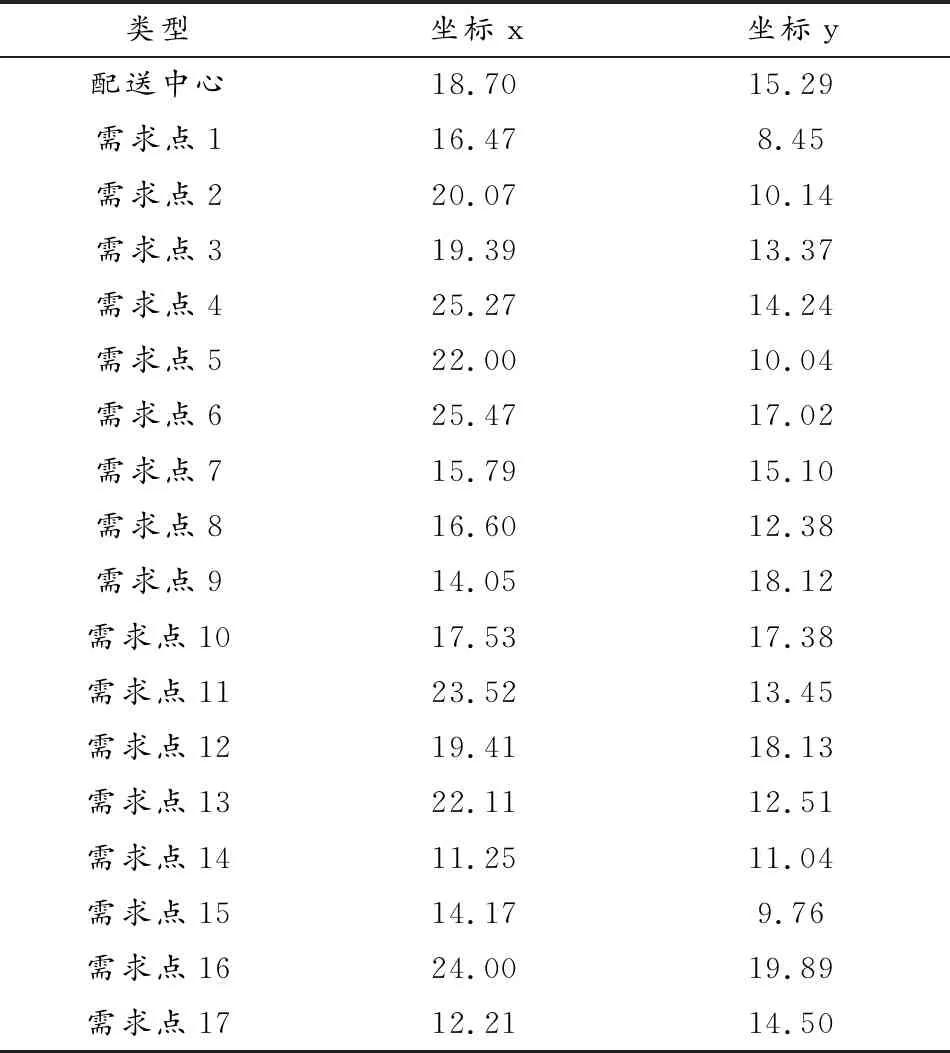
表1 配送中心和需求點坐標

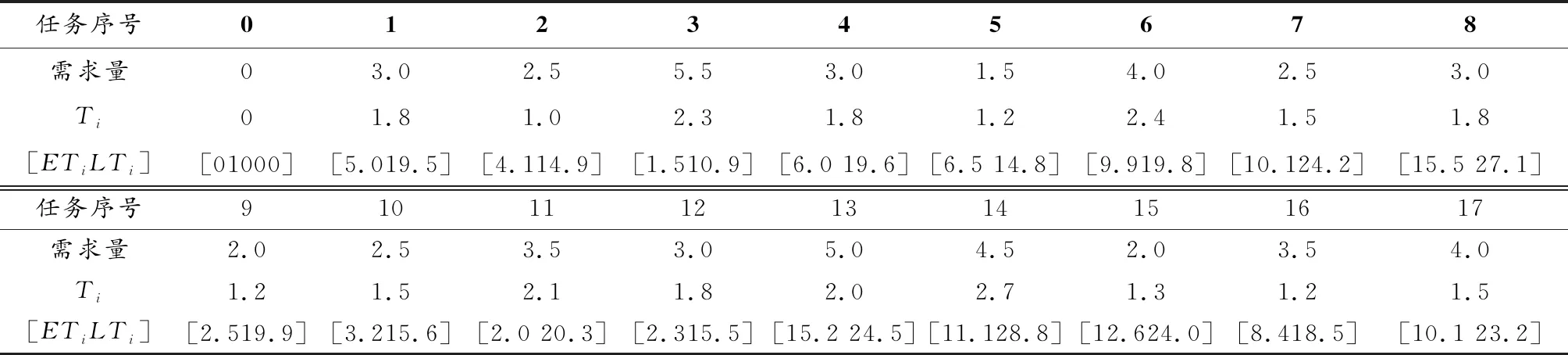
表2 配送中心和用戶需求

將IWOA和WOA、PSO、GA進行對比，不同算法參數設置如下：(1)WOA參數：種群規模N=50、最大迭代次數Maxgen=500。(2)粒子群算法(particle swarm optimization algorithm，PSO)：種群規模N=50、最大迭代次數Maxgen=500、學習因子c1=c2=2、慣性權重w=0.2。(3)遺傳算法(genetic algorithm，GA)：種群大小N=50、最大迭代次數Maxgen=500交叉概率Pc=0.7和變異概率Pm=0.1，對比結果如圖3～圖7所示。

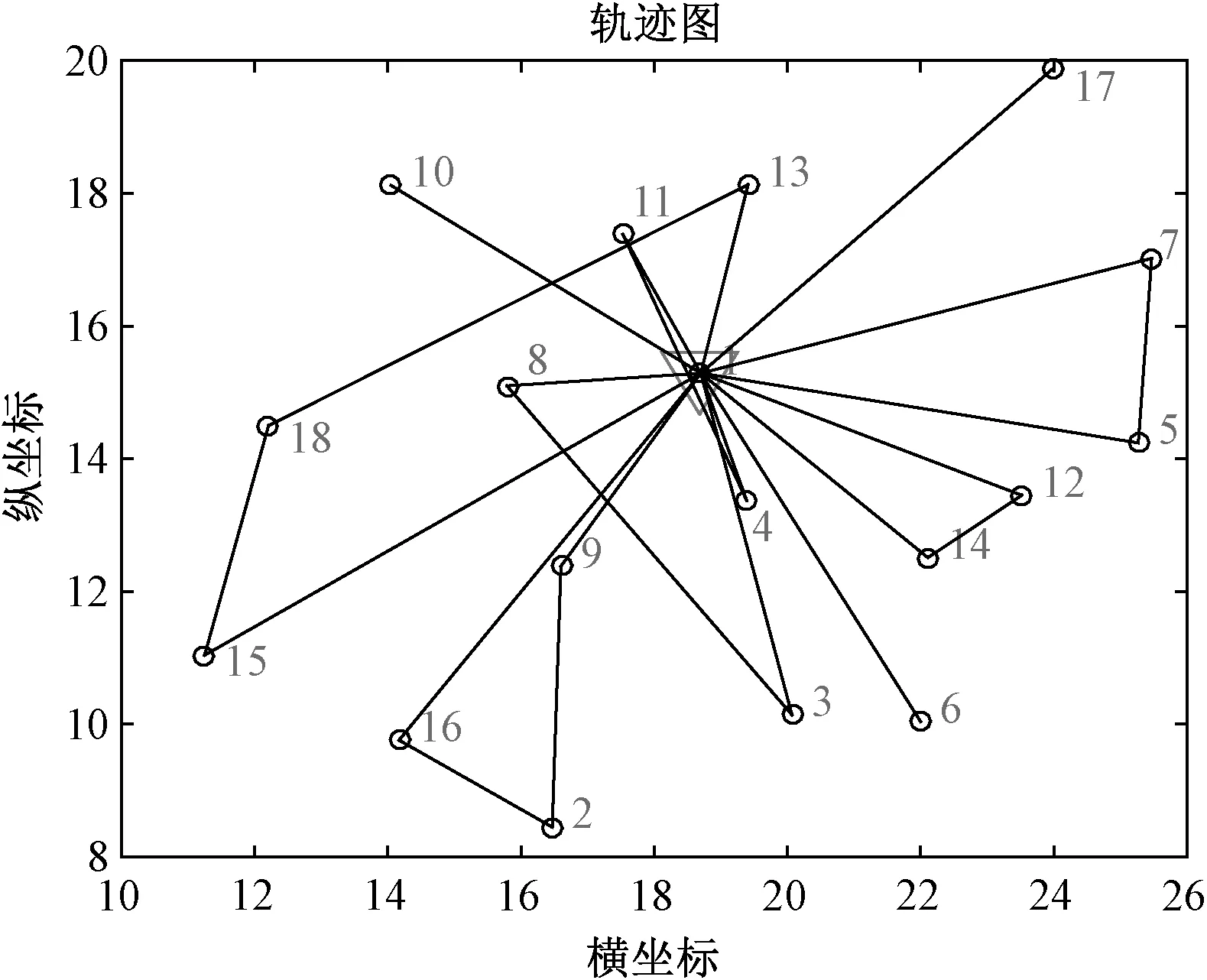
圖3 IWOA配送路徑圖

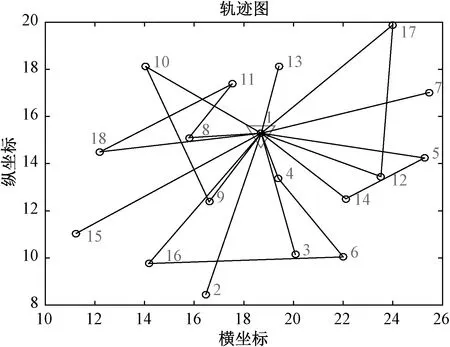
圖4 WOA配送路徑圖

圖5 PSO配送路徑圖

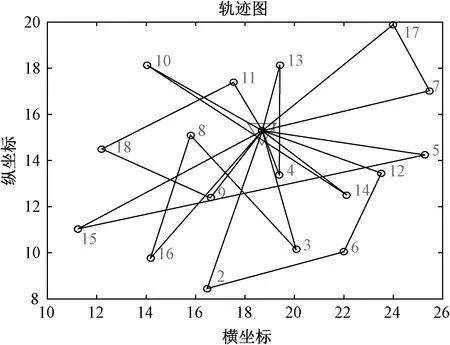
圖6 GA配送路徑圖

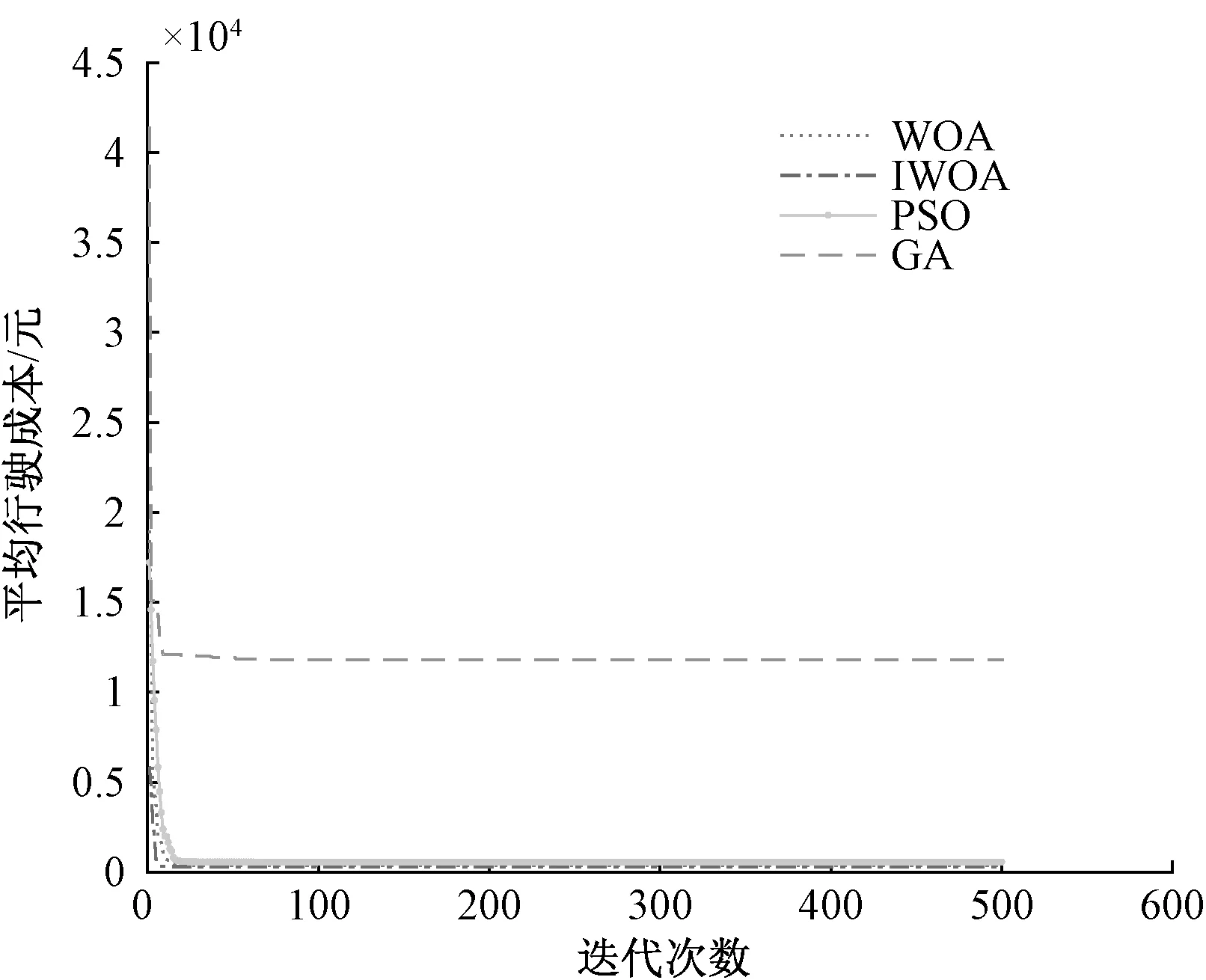
圖7 尋優對比曲線

由表3可知，GA、PSO和GA進行物流車輛配送路徑規劃時，GA的平均行駛成本和行駛里程分別為603.0031元和139.5906km，PSO的平均行駛成本和行駛里程分別為565.8001元和138.9368km，WOA的平均行駛成本和行駛里程分別為359.3838元和130.2608km，而改進的IWOA的平均行駛成本和行駛里程分別為337.6755元和129.1333km。與WOA、PSO和GA相比，在行駛里程和平均行駛成本方面，IWOA進行車輛路徑規劃的成本最低且行駛里程最短。由圖7尋優對比曲線可知，IWOA進行車輛路徑規劃尋優具有更快的收斂速度和更低的平均行駛成本。通過綜合對比驗證了IWOA進行物流車輛配送路徑優化的有效性和可靠性。

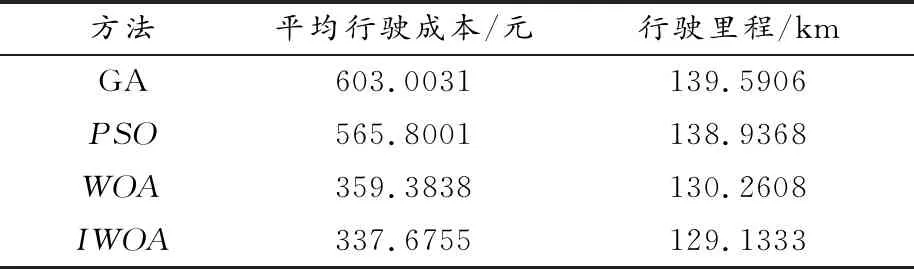
表3 IWOA、WOA、PSO和GA對比結果

4 結論

本文運用改進的鯨魚優化算法求解物流配送路徑規劃問題。研究結果表明，與WOA、PSO和GA相比，在搜索時間和平均行駛成本方面，IWOA進行車輛路徑規劃的配送成本最低且行駛里程最少，為物流配送車輛路徑優化提供了新的方法。