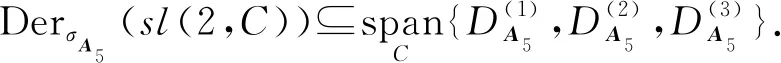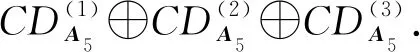李代數sl(2,C)的斜導子
易 揚,遠繼霞
(黑龍江大學數學科學學院,黑龍江 哈爾濱 150080)
0 引言
李代數是現代數學的重要基礎,促進了Kac-Moody代數、量子群等新興分支的出現和發展,和群論、拓撲、微分幾何以及理論物理都有密切聯系,并在上述領域中有許多的應用.研究者對于李代數的導子做了許多研究工作.[1-9]文獻[5]引出斜導子是通常導子的自然推廣之一,也是廣義導子和時滯導子的一個推廣.文獻[2-4]中已經得到了一些關于廣義斜導子的結果.許多學者對素環和半素環上的偏斜導子做了許多細致深刻的探討.文獻[5]介紹了素環和半素環上的對稱斜3-導子的概念.文獻[1]將廣義斜導子的定義推廣到R的右Martindale商環Q上.本文將文獻[7]中斜導子的定義推廣到了李代數上,并研究了sl(2,C)的自同構所確定的斜導子的形式,得出對sl(2,C)任意的自同構σ,σ-導子空間是1維或3維的.
1 預備知識
本文設C是復數域,所有的向量空間都是在復數域C上的向量空間.設V是C上的向量空間,End(V)為V上的所有線性變換構成的集合.對于一個李代數g,記Autg為g的自同構群.
定義1[7]對于σ∈Autg,令D是g上的線性變換,滿足
D([x,y])=[Dx,y]+[σ(x),Dy],?x,y∈g,
(1)
則稱D為李代數的斜導子(或σ-導子).
令Derσg為g的所有σ-導子構成的集合.注意到Derσg對于線性變換的加法和數乘構成一個線性空間,將其稱為g的σ-導子空間.顯然任意一個李代數的導子是id-導子,因此斜導子是導子的推廣.本文將研究典型李代數sl(2,C)的σ-導子.回憶李代數sl(2,C)的結構,sl(2,C)是由跡為零的2×2矩陣構成的李代數,不難驗證它有以下的一組基:
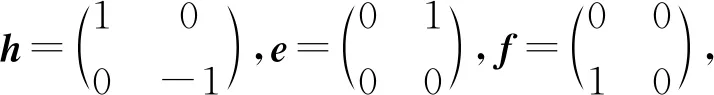
而且基元之間的運算滿足下面的關系式
[h,e]=2e,[h,f]=-2f,[e,f]=h.
2 斜導子的刻畫
下面進行斜導子的刻畫,引入如下引理:
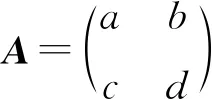
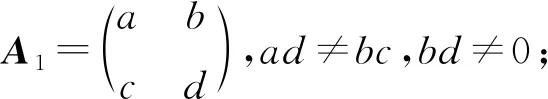
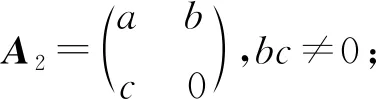
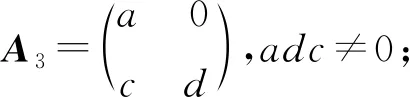
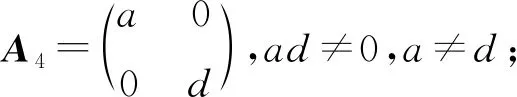
談話前,盧一平表現得漫不經心若無其事。他和郝桂芹回顧了家里的收支狀況,感嘆物價飛漲,報怨收入微薄,接下來,是感嘆孩子借讀的開銷和老人醫護費的攀升。看見郝桂芹連連點頭、默認,盧一平知道火候到了,機會來了。他開始分析了,他開始總結了。總結的結果,是這樣下去將會坐吃山空。得出的結論,是必須改弦易轍才能扭轉局面。
證明由于A可逆,故ad-bc≠0,分成bd≠0和bd=0討論.當bd≠0時,即為情況(1).當bd=0時,可分為b=0和d=0.若d=0,即為情況(2).若b=0,可分為c≠0和c=0,a≠d以及c=0,a=d討論.c≠0即為情況(3);c=0,a≠d即為情況(4);c=0,a=d即為情況(5).
引理2[6]對每個可逆陣A,令σA(X)=A-1XA,則σA是李代數sl(2,C)的自同構,且sl(2,C)的所有自同構是映射XA-1XA所組成的集合.
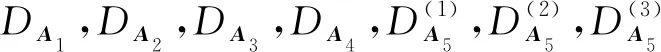
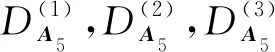
命題1 DerσAi(sl(2,C))=CDAi,i=1,2,3,4.
證明“?”關系顯然成立,下面證明“?”關系.
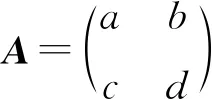
σA(X)=A-1XA.
σA:h[(da+bc)h+2bde-2acf];
e[dch+d2e-c2f];
f[(-ba)h-b2e+a2f].
設D∈DerσAi(sl(2,C)),且

其中m,n,p,q,s,t,u,r,w∈C.根據(1)式,得到下面的等式:
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
由(2)—(10)式,整理得到以下等式:
2bdu+2acq=0,4bcq-4bdm=0,-4bcu-4acm=0,
-4adr-4acn=0,4dat-4bdp=0,2dcq-2d2m=0,
2bau+2a2m=0,-2dcr-2c2n=0,-2bat+2b2p=0,
(ad-bc)m-(ad-bc)w-b2r-a2s=0,(ad-bc)q+2(ad-bc)p-2bas+2b2n=0,
(-ad+bc)u-2(ad-bc)n-2dcw-2c2p=0,-2(ad-bc)p-b2u-a2q=0,
(-2n-u)(ad-bc)+2bdr+2acs=0,2(ad-cb)m+4bcs-4bdn=0,
(2p+q)(ad-bc)+2bdw+2act=0,-4bcw-2(da-bc)m-4acp=0,
(ad-bc)s-(ad-bc)m+d2w+c2t=0,(cb-ad)q+2dct-2d2p=0,
-4(ad-bc)t-2baq+2b2m=0,(2a2-2ad+2cb)p+2baw=0,
2(ad-bc)n+d2u+c2q=0,4(ad-bc)r-2dcu-2c2m=0,
(ad-bc)u+2bar+2a2n=0,(ad-bc-a2)t-b2w=0,
(d2-ad+bc)r+c2s=0,2(ad-cb-d2)n+2dcs=0.
當A=A1時,由上述等式解得:
于是
同理可得,當A=A2時,等式的解如下:
于是
當A=A3時,等式的解如下:
于是
當A=A4時,等式的解如下:
于是
綜上所述,DerσAi(sl(2,C))?CDAi,i=1,2,3,4.
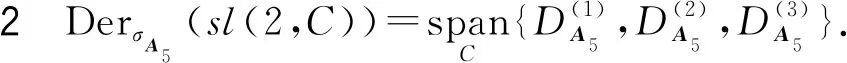

上述等式的解如下:
p=-1/2q,s=-dw/a,u=-2n,m=t=r=0.
于是