基于“一題多解”的初中數(shù)學(xué)核心素養(yǎng)培養(yǎng)

丁淑琳，王羅那，黃 韜

(1.湖州市環(huán)渚學(xué)校，浙江 湖州313000；2.湖州師范學(xué)院 理學(xué)院，浙江 湖州 313000)

數(shù)學(xué)核心素養(yǎng)是人們通過數(shù)學(xué)學(xué)習(xí)建立起來的認(rèn)識、理解和處理周圍事物時所具有的品質(zhì)，是人們與周圍環(huán)境產(chǎn)生相互作用時表現(xiàn)出來的思考方式和解決問題的策略[1].一題多解是利用不同的思維方法對同一個問題使用兩種或兩種以上的方法進(jìn)行求解.其本質(zhì)是緊扣習(xí)題本身，靈活運(yùn)用定義、定理等基本原理，通過不同的途徑呈現(xiàn)問題的解答過程.

在教學(xué)過程中，合理滲透一題多解的思想，有利于促進(jìn)學(xué)生靈活運(yùn)用數(shù)學(xué)知識能力，活躍學(xué)生的數(shù)學(xué)思維，提高學(xué)生分析問題和解決問題的能力，從而激發(fā)學(xué)生對數(shù)學(xué)學(xué)習(xí)的興趣[2].如何恰當(dāng)?shù)貙?shí)施一題多解，培養(yǎng)學(xué)生的數(shù)學(xué)核心素養(yǎng)，本文以初中數(shù)學(xué)例題為例，通過一題多解進(jìn)行分析探討.

1 試題呈現(xiàn)

并非所有的例題都適合一題多解，一題多解的題目需具備代表性、綜合性、靈活性等特點(diǎn)，既要包含基本知識點(diǎn)，又要有一定的知識廣度和難度.本文選擇以下例題作為實(shí)施一題多解的載體.

例如圖1,在平面直角坐標(biāo)系中,直線y=-x+m(m≠0)分別交x軸、y軸于A、B兩點(diǎn),已知點(diǎn)C(3,0).設(shè)點(diǎn)P為線段OB的中點(diǎn),連結(jié)PA、PC,若∠CPA=45°,則m的值是( ).

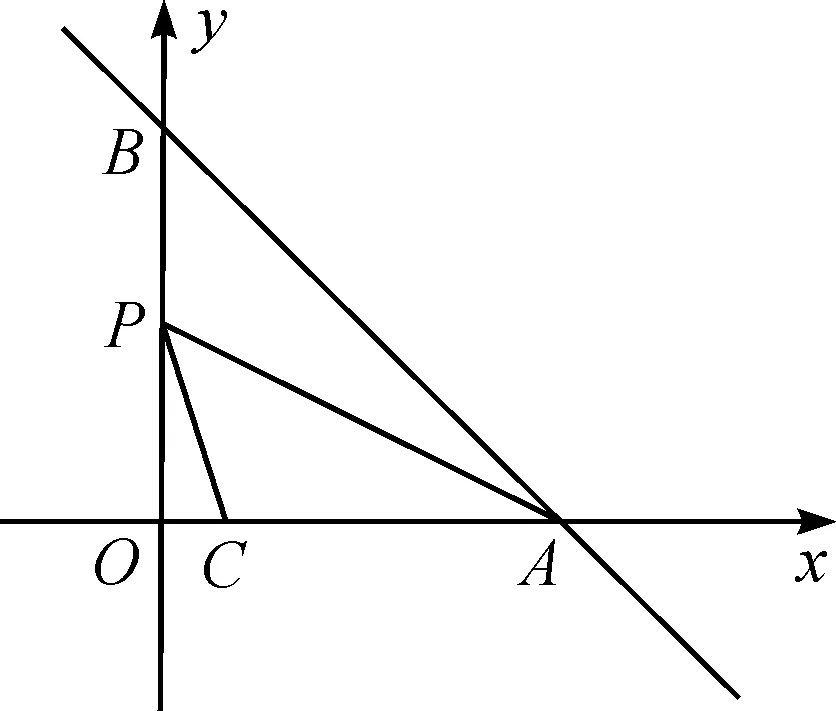
圖1 教學(xué)例圖Fig.1 Teaching illustration

1.1 試題分析

本題是一次函數(shù)與幾何相結(jié)合的題目，主要考查待定系數(shù)法求一次函數(shù)解析式、相似三角形的判定與性質(zhì)等知識點(diǎn).題目的呈現(xiàn)以函數(shù)為主線，聚焦圖形與幾何問題，雖然外表樸實(shí)無華，但內(nèi)涵卻很豐富.題目構(gòu)思緊扣《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2011年版)》要求，以培養(yǎng)學(xué)生的核心素養(yǎng)為出發(fā)點(diǎn)，引導(dǎo)學(xué)生在解決實(shí)際問題的過程中總結(jié)經(jīng)驗(yàn)，探究與感悟知識的發(fā)生發(fā)展過程，挖掘問題本質(zhì)，幫助學(xué)生獲得知識和素養(yǎng)水平的雙重提升[3].根據(jù)題意可得到以下幾個條件：①直線斜率為1，即∠ABO=∠BAO=45°；②P為線段OB中點(diǎn)；③∠CPA=45°.根據(jù)學(xué)生的已有知識和解題經(jīng)驗(yàn)，本題可應(yīng)用相似、等腰直角三角形等知識來解題[4].在教學(xué)中教師應(yīng)更多地讓學(xué)生去聯(lián)想一些基本模型，這才是解題的關(guān)鍵.但學(xué)生解題的難點(diǎn)是如何通過作輔助線將已有的條件聯(lián)系起來，這需要學(xué)生具備較強(qiáng)的數(shù)學(xué)素養(yǎng)，也是教師在教學(xué)中需要重點(diǎn)培養(yǎng)的.

經(jīng)以上分析，結(jié)合教學(xué)經(jīng)驗(yàn)與反思，本文對此題擬定了一題多解滲透核心素養(yǎng)的實(shí)施路徑，見表1.

表1 一題多解滲透核心素養(yǎng)的實(shí)施路徑

1.2 解法展示

視角1利用常見模型構(gòu)造相似.根據(jù)題目條件的特殊性很容易聯(lián)想到一些解題的基本模型，如“一線三等角”“半角模型”“K字型”“12345”等.利用模型進(jìn)行一題多解能夠培養(yǎng)學(xué)生的幾何直觀、推理能力和模型思想.

思路1構(gòu)造“一線三等角”模型.“一線三等角”模型是一種常見的建立三角形相似的方法.該題目只有兩個等角，所以可以利用45°角構(gòu)造等腰直角三角形，從而構(gòu)造“一線三等角”模型，并在構(gòu)造時過C點(diǎn)作輔助線，再利用相似三角形的基本性質(zhì)列出方程[5].

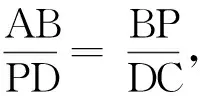
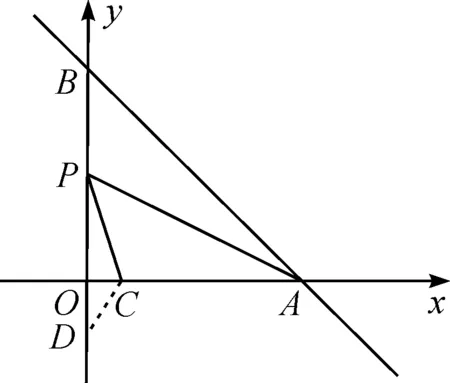
圖2 教學(xué)例圖Fig.2 Teaching illustration

思路2構(gòu)造“半角模型”.“半角模型”是一種常見的基本模型，這類問題一般利用旋轉(zhuǎn)得到全等三角形，進(jìn)而得到線段之間的關(guān)系[5].本題由于△BOA與點(diǎn)P的特殊性，所以可以構(gòu)造“半角模型”.

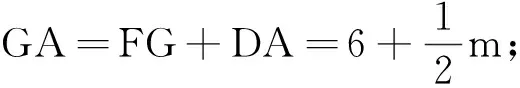
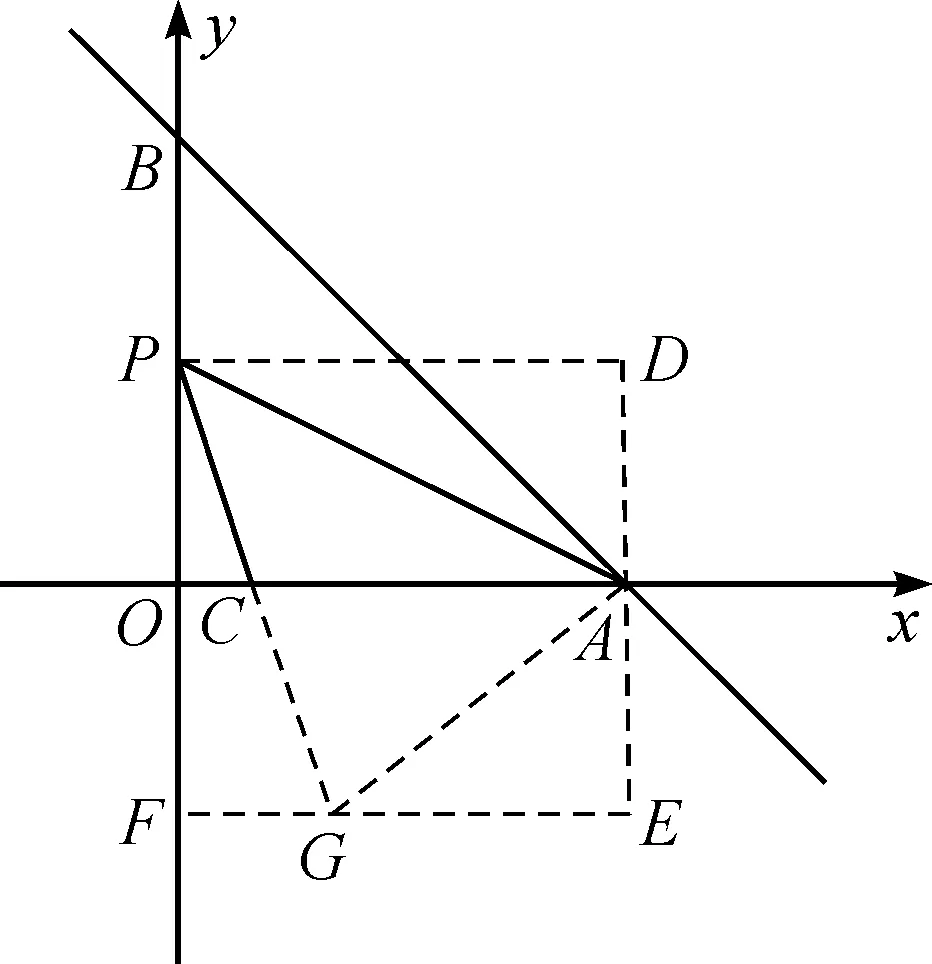
圖3 教學(xué)例圖Fig.3 Teaching illustration

思路3構(gòu)造“K字型”模型.“K型全等”和“K型相似”模型是一個基本圖形.利用該模型不僅可以找到全等三角形，還可以找到相似三角形，從而進(jìn)行邊長的轉(zhuǎn)化和尋找等量關(guān)系.本題有45°角，所以可以構(gòu)造“K型全等”模型.

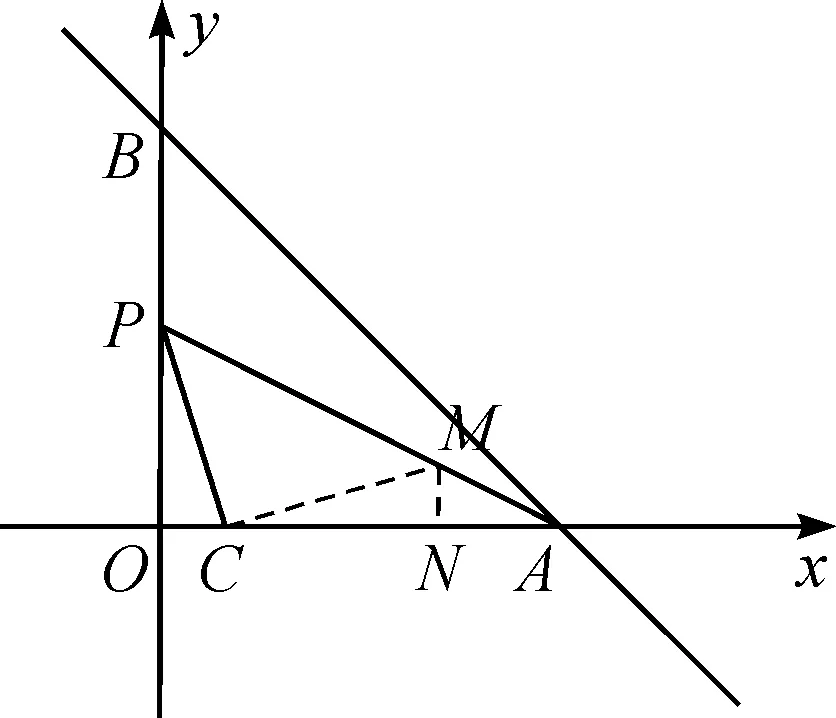
圖4 教學(xué)例圖Fig.4 Teaching illustration

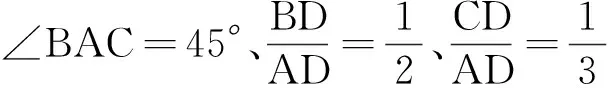
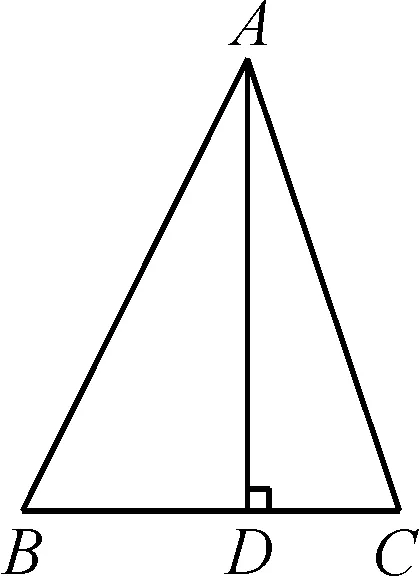
圖5 教學(xué)例圖Fig.5 Teaching illustration

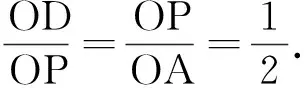
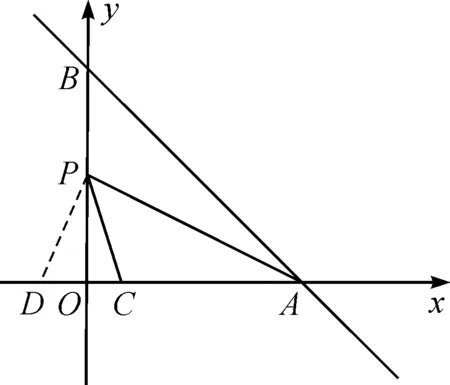
圖6 教學(xué)例圖Fig.6 Teaching illustration

視角2直接構(gòu)造相似.相似三角形的構(gòu)造除了視角一中的4個思路外，還可直接從本題的條件出發(fā)，利用45°角構(gòu)造等腰直角三角形相似和母子型相似.這是一種很好的思路，更加注重通性通法，能培養(yǎng)學(xué)生的幾何直觀和推理能力.

思路5作垂線，構(gòu)相似.在平面直角坐標(biāo)系中“利用垂直構(gòu)造相似”是一種常用的方法.本題結(jié)合45°角構(gòu)造等腰直角三角形與相似，一箭雙雕，尋找兩種圖形之間的線段關(guān)系，從而找到等量關(guān)系.

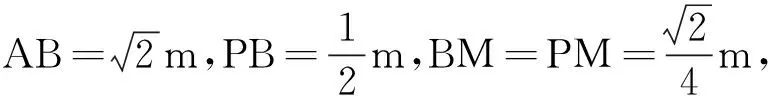
圖7 教學(xué)例圖Fig.7 Teaching illustration

思路6做平行，構(gòu)相似.利用平行線構(gòu)造“母子型”相似模型.基于∠CPA=45°，而對應(yīng)的比例線段都較容易表示，“母子型”相似也是常用的一種基本模型，所以該方法是一種較好的解題思維.

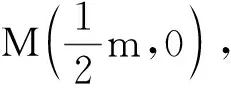
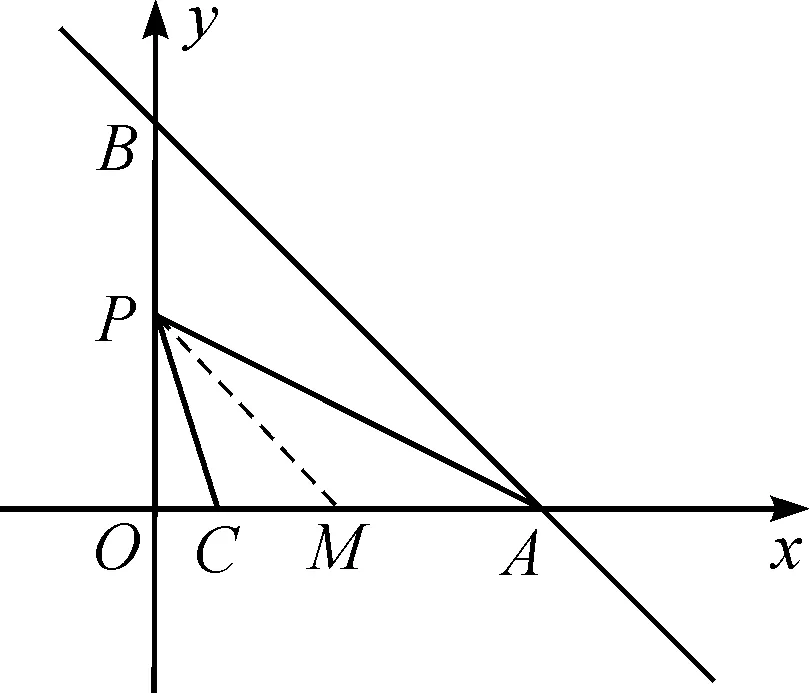
圖8 教學(xué)例圖Fig.8 Teaching illustration

視角3構(gòu)造輔助圓.

思路7利用“四點(diǎn)共圓”.“四點(diǎn)共圓”是一種常見的基本圖形，它可以運(yùn)用同弧所對的圓周角相等、半徑相等，以及直徑所對的圓周角是直角等知識點(diǎn)[5].如果學(xué)生能突破常規(guī)解法，并利用輔助圓解決問題，那么他們的創(chuàng)新能力就能得到很大提升.

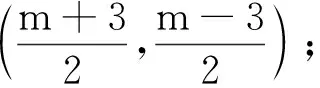
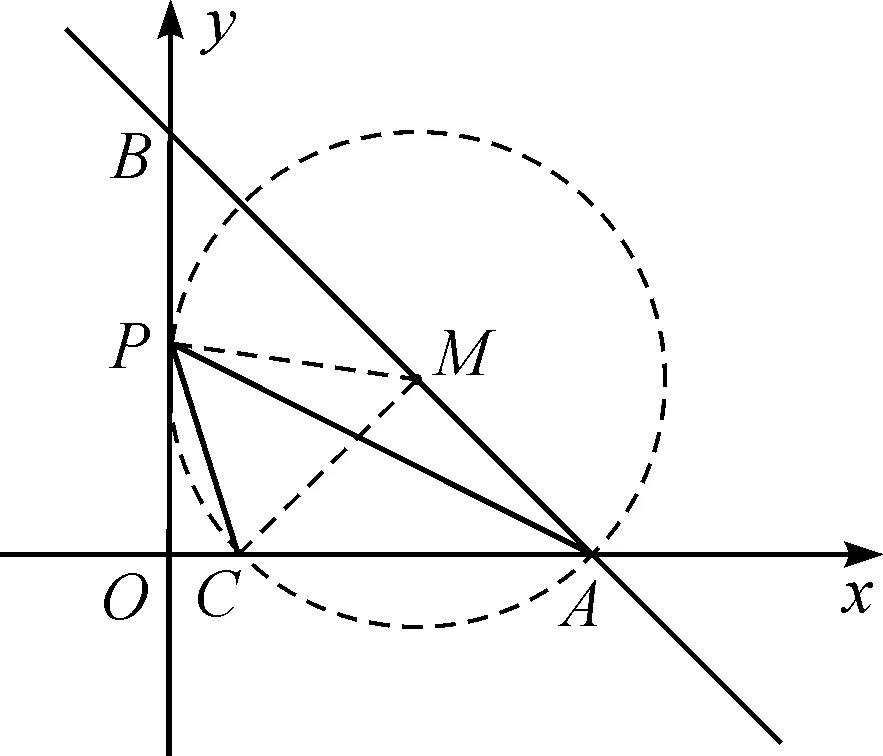
圖9 教學(xué)例圖Fig.9 Teaching illustration

視角4利用已有性質(zhì)或公式.

思路8利用角平分線性質(zhì).由于45°角是90°角的一半，構(gòu)造了角平分線，因此可以利用三角形內(nèi)角平分線的基本性質(zhì).利用45°角補(bǔ)全直角也是一種常用的手段.

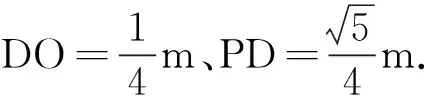
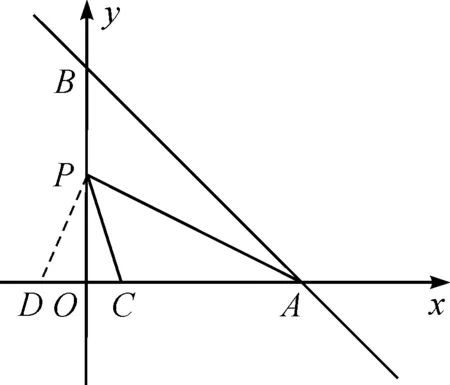
圖10 教學(xué)例圖Fig.10 Teaching illustration

思路9利用三角函數(shù)公式.本解法不同于以上解法，是用代數(shù)的方法來求解幾何問題，無需添加輔助線，通常把這種解決問題的方法稱為解析法.該思路主要抓住∠CPA是45°和點(diǎn)P、C、A都是已知或可以用含m的代數(shù)式直接表示這一特征，聯(lián)想到兩直線夾角公式.這對提前學(xué)過高中知識的學(xué)生來說是比較自然的解法.

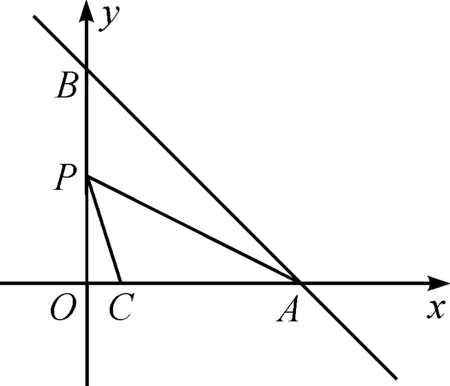
圖11 教學(xué)例圖Fig.11 Teaching illustration

2 教學(xué)導(dǎo)向

(1) 注重基礎(chǔ)知識，強(qiáng)化基本技能.數(shù)學(xué)基礎(chǔ)知識是一切解題的“源泉”,也是數(shù)學(xué)教學(xué)的起點(diǎn).數(shù)學(xué)基本技能是數(shù)學(xué)學(xué)習(xí)的基本要求，也是數(shù)學(xué)能力與數(shù)學(xué)核心素養(yǎng)的基本體現(xiàn).數(shù)學(xué)教學(xué)不能只注重解題而輕視數(shù)學(xué)基礎(chǔ)知識和基本技能，而要重視數(shù)學(xué)基礎(chǔ)知識的鞏固，以及基本技能的形成與提煉.

(2) 熟悉基本模型，明確解題方向.波利亞說：“解題的成功要靠正確的思路選擇，要靠從可以接近它的方向攻擊堡壘.”基本模型是解決較難幾何問題的一個很好的突破口，從未知圖形中構(gòu)造基本模型，利用基本特征和結(jié)論往往可以化難為易，順利得解[5].教師要通過構(gòu)造基本模型實(shí)現(xiàn)“學(xué)會建模”的教學(xué)理念，加強(qiáng)模型的運(yùn)用，明確解題方向.

(3) 呈現(xiàn)多樣解法，內(nèi)化核心素養(yǎng).無論是哪種方法，其本質(zhì)都是抓住題目中的條件特征，并對其進(jìn)行分解和重組.多樣解法的生成與諸多因素有關(guān).在平時教學(xué)中,教師應(yīng)通過多樣解法的呈現(xiàn)引導(dǎo)學(xué)生掌握幾何基本模型結(jié)構(gòu),提煉幾何證明的通性通法,使學(xué)生學(xué)會重新分解和組合題目條件，學(xué)會從數(shù)量和圖形中尋求解題的突破，增強(qiáng)學(xué)生的合情推理能力.

(4) 關(guān)注初高銜接，提升解題能力.近年來，注重初高中知識銜接問題是中考數(shù)學(xué)的一大特點(diǎn)，很多高中的知識點(diǎn)在初中也稍有涉及.或以閱讀材料形式給出，或可以直接使用，簡化解題過程等.如解答本文例題時使用的角平分線性質(zhì)、三角函數(shù)公式等，教師應(yīng)做好初高中知識方法銜接的講解與應(yīng)用，使學(xué)有余力的學(xué)生提升解題能力和水平.

3 結(jié) 語

“掌握數(shù)學(xué)就意味著要善于解題”，這句話點(diǎn)明了數(shù)學(xué)教學(xué)的根本目的——提高學(xué)生探索和解決問題的能力，培養(yǎng)學(xué)生的數(shù)學(xué)創(chuàng)新精神.中高考這些選拔性考試具有較強(qiáng)的導(dǎo)向性，因此培養(yǎng)、提高學(xué)生的數(shù)學(xué)思維能力，有效地將核心素養(yǎng)培養(yǎng)貫穿于數(shù)學(xué)教學(xué)全過程，是實(shí)際數(shù)學(xué)教學(xué)的重要一環(huán).“一題多解”教學(xué)既能激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，又能培養(yǎng)學(xué)生的創(chuàng)新意識和創(chuàng)新思維，還可以提高學(xué)生的思維能力和解題能力，從而提升學(xué)生的數(shù)學(xué)核心素養(yǎng).隨著人工智能時代的到來，“計算思維”等新素養(yǎng)對學(xué)生的關(guān)鍵能力與素養(yǎng)的養(yǎng)成至關(guān)重要，因此合理利用數(shù)字化、信息化資源將有助于進(jìn)一步打開學(xué)生的解題思路與視角[6].作為一線教師既要授之以“魚”，更要授之以“漁”，讓學(xué)生能真正高效地學(xué)好數(shù)學(xué).