α-Shape算法雙機器人協作工作空間研究

朱良麒，丁力平，陳文亮，周志光

（1.南京航空航天大學機電工程學院，江蘇 南京210016；2.江蘇雷利電機股份有限公司 工程中心，江蘇 常州213011）

1 引言

機器人工作空間是指機器人末端坐標系的原點在空間中所能到達的區域［1］，是衡量機器人工作能力的重要運動學指標之一［2］，而雙機器人協作工作空間是指參與協作的機器人的工作空間所形成的交集［3］。工作空間與協作工作空間在機器人的機構設計、安裝布局、路徑規劃、避碰、機器視覺和最佳操作位形等研究方面有著非常重要的參考意義，是當下機器人領域的研究熱點，但同時也是技術難點。

研究和分析機器人協作工作空間是提高機器人協作效率和確保其安全生產的關鍵。目前為止，國內外學者在雙機器人協作工作空間問題求解上采用的方法與單個機器人工作空間求解方法類似，主要有：幾何圖解法、解析法和數值法［4］。尤其是近年來隨著電子計算機技術的發展，蒙特卡洛數值方法［5］在機器人工作空間的求解上得到了廣泛應用，并且同時也比較適合分析協作工作空間，該方法不涉及逆運動學求解，算法相對較簡單，具有較強的通用性。但這種方法生成的工作空間點云集只是對實際工作空間的一種近似表示，無法為工程實踐提供較為具體的數值分析。因此很多學者將研究目標集中在由工作空間點云獲得工作空間曲面的方法尋求上［6～8］，其主要工作一般是對工作空間點云分層，再逐層提取邊界點，并擬合為邊界曲線，最后求出工作空間包絡曲面。該方法求解過程中邊界點提取以及包絡線求解較復雜，且通用性不強，更難對協作工作空間進行求解。

為了使工作空間可視化和數字化，提高應用性，范啟忠等［9］運用了a-Shape算法處理單個機器人工作空間點云，對工作空間進行三維重建，并通過調整a參數大小得到了較高的重建精度，該方法具有較好通用性。基于此，這里進行更深入的研究，通過一定算法獲取雙機器人協作工作空間的點云后，運用a-Shape算法分別對機器人工作空間以及協作工作空間進行重建，更加突顯該算法的優越性，對機器人協作技術奠定了基礎。

2 協作工作空間定義及點云獲取

2.1 雙機器人協作工作空間定義

一般情況下，我們將參與協同作業的兩個機器人分別設置為主、從機器人，由機器人運動學關系可知，其TCP點位置矢量與關節位移存在一一對應的函數關系，可表示為：

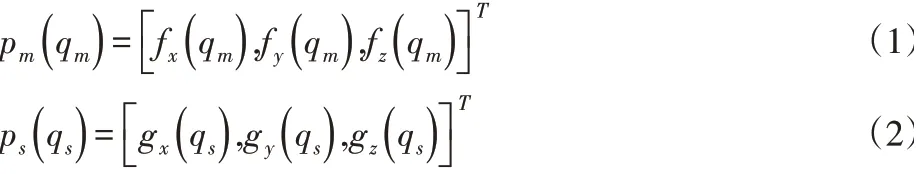
式中：q-關節變量；p-位置矢量；下標m、s-主機器人與從機器人，函數f與g由機器人正運動學得出。

為了簡化計算，實際中一般選取世界坐標系Fw與主機器人基坐標系一致。則主機器人工作空間可表示為：

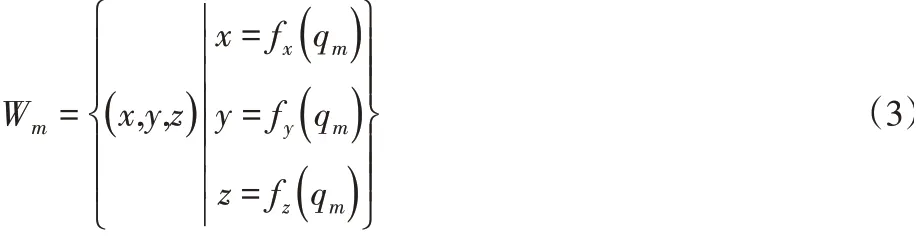
從機器人在其基坐標系Fbs下的工作空間可表示為：

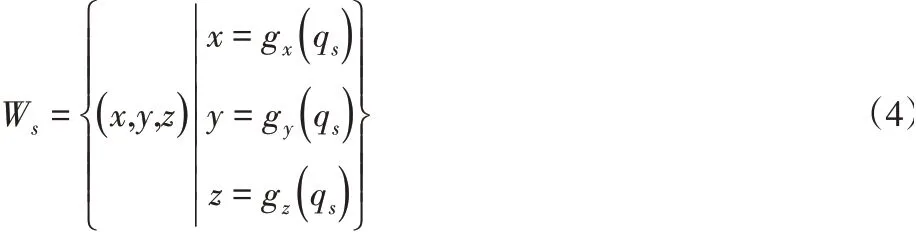
故雙機器人協作工作空間可表示為：

公式（3）～（6）用集合形式定義了機器人的工作空間與協作工作空間，其解集應是連續的，但這種表達形式不直觀，解析過程太復雜，難以直接運用。

2.2 蒙特卡羅法機器人工作空間點云模型

蒙特卡羅法的思想是通過大量隨機樣本，對系統的特性進行模擬，進而得到問題的近似解。對機器人工作空間建立起隨機概率模型，將末端TCP點的空間位置看做隨機數，當隨機樣本足夠大時，這些隨機點構成的區域就近似代表了機器人的工作空間。因此，在關節空間內隨機產生大量組關節位移q，通過一映射得到末端坐標系原點的位置隨機點，這些點的集合就可以表示為機器人工作空間的離散模型，具體計算步驟如下：

（1）在各關節變量范圍［qimin，qimax］內取隨機值，得到N組關節矢量；（2）進行機器人正運動學方程推導，并將上一步得到的N組關節矢量帶入，得到對應的N個末端TCP點即隨機點；（3）利用計算機的繪圖功能將所有隨機點以描點的方式顯示，得到工作空間的點云圖。

2.3 協作工作空間點云獲取

獲取協作工作空間的點云圖，最簡單直接的方法是求解主、從機器人點云集的交集，找出重合的點。但由于點運數據是離散的，這種方法只能搜索到極少部分的點，忽略了處于協作工作空間內而沒有相互重合的點。如圖1所示，方形點表示主機器人的隨機點，圓形點表示從機器人的隨機點，可以看到大多數的點位于“協作區”卻不能按照求交集的方法尋到，誤差過大。

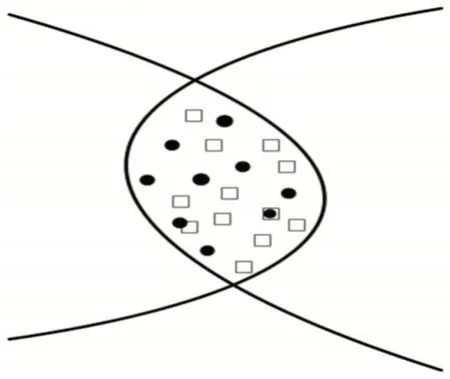
圖1 協作區域隨機點分布示意圖Fig.1 Schematic Diagram of Random Point Distribution in the Collaboration Area

為了獲得更多的協作工作空間點，可以采取計算點與點距離并加入一定閾值的判斷方法：遍歷主機器人點云集的每個隨機點再依次計算該點與從機器人點云集的隨機點的距離，設置允許的閾值為e，若存在滿足的兩點，則認為pm、ps就是協作工作空間點，待遍歷完成后，就獲得了協作工作空間的原始點云數據。該方法可以提取到大部分位于協作區域而沒有相互重合的點。獲得雙機器人協作工作空間的離散模型即點云集后，可以通過繪圖方式粗略地看到點云的大體分布情況。

3 α-Shape算法工作空間輪廓提取

3.1 α-Shape算法原理

文獻［9］第一次給出了面向點云數據α-Shape的通用概念，并給出了α-Shape族的一種計算方法α-Shape。算法可以從一堆無序離散點集中提取邊緣，并通過一定的算法獲得重建的圖形，平面點云的α-Shape為一個多邊形，三維空間點云集的α-Shape則是一個多面體。R2空間中，其原理如圖2所示，設S為一有限無序點集，α為（0，∞）范圍內的實數，假想一個半徑為α的圓在點集S外滾動，若α足夠大時，這個圓就不會掉進點與點之間的空隙，滾落到點集內部，其滾動的痕跡便是該點集的邊界線。

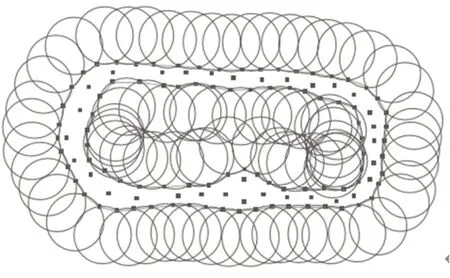
圖2 α-Shape算法原理圖Fig.2 Schematic Diagram of α-Shape Algorithm

具體的判別方法可以描述為：點集S由n個點構成，n個點組成n*（n-1）條線段，過點集S中任意兩點P1、P2作半徑為α的圓（一般可以得到兩個圓），如果有一個圓內部不包含點集S中的其他任何點，就認為P1、P2是邊界點，其連線為邊界線段。所以，當α值非常小時，則每個點都在邊界上；若α很大（α→∞）時，則形成的邊界線為點集S的凸包［10］。

同理，R3空間中的α-Shape算法則是通過點集S中的三點作半徑為α的球來判別邊界點，并在得到的邊界點處建立三角片面，以三角片面的形式重構出曲面。重構結果隨著α取值的不同而變化，α值偏大會保留更多的三角面片，表現為點集的凸包，α值偏小則會出現空洞，α為0時，α-Shape退化為原始的點集［11］。

3.2 基于形體體積值的參數α確定

α-Shape算法直觀的表達了點云集的形狀，同時其精細程度由α控制。因此，為了獲得理想的三維重構效果，需要確定出合適的參數α值。理論上，多自由度關節型機器人的工作空間類似球狀，受各關節轉動范圍限制和奇異性等因素的影響，空間分布會有所變化，其點云的三維重構結果表現為一定形體的封閉空間。因此，可以考慮將形體的體積計算值作為參考衡量重構效果。這里基于MATLAB volume（）函數對建立的三維α-Shape形狀體積進行求解，計算大量組不同參數ai下對應的多面體體積值Vi，將結果以坐標（ai，Vi）的形式記錄，得到體積隨參數變化的趨勢關系，進而根據三維α-Shape形狀特點分析并確定參數a的值。

4 實例分析與驗證

以兩臺ABB公司的IRB140型6軸多用途工業機器人為例，對文中方法進行驗證。該型機器人的實物圖如圖3所示，采用DH法［12］建立連桿坐標系，結果如圖4所示，相應的連桿參數如表1所示。機器人正運動方程可以表示為：

圖3 IRB140機器人實物Fig.3 The Object of IRB140 Robot

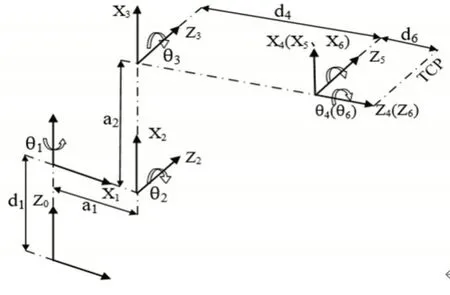
圖4 機器人連桿坐標系Fig.4 Robot Link Coordinate System

考慮末端安裝有法蘭，主從機器人實際的TCP點坐標系到各自基坐標系的總變換為：

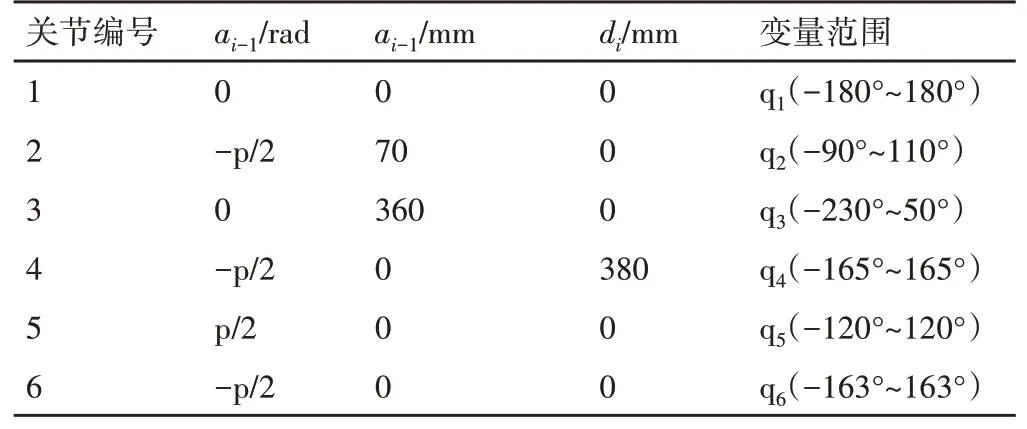
表1 IRB140機器人D-H參數Tab.1 The D-H Parameters of IRB140 Robot

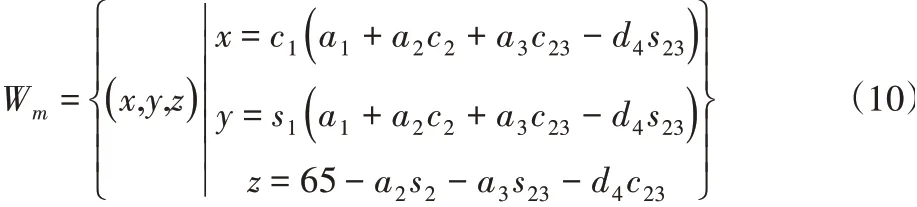
為便于從機器人工作空間計算，設兩臺機器人采取典型的地面式-地面式且兩者相對的安裝方式，基坐標系原點之間距離為1.2m，則主、從機器人基坐標系間的旋轉矩陣和平移矩陣為：

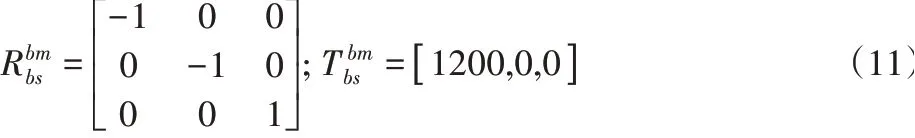
進而由公式（5）計算得到從機器人的工作空間解集為：

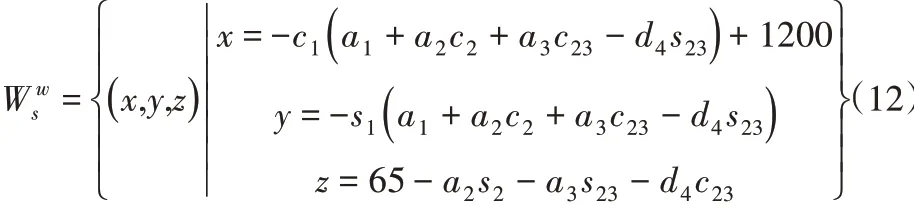
式中：si、ci-sinqi和cosqi，sij、cij-sin（qi+qj）和cos（qi+qj），且qimin￡qi￡qi-max，i=1，2，3。

根據上述主、從機器人工作空間解集Wm和Wsw，按照1.2中方法，可以分別得到兩臺機器人工作空間的點云數據。一般情況下，隨機點數量越多，機器人工作空間計算精度越高，但當隨機點數多達一定數量時，工作空間點云圖像已經非常清晰，增大隨機點數量的意義不大。這里多次試驗后最終確定主、從機器人各取隨機點15萬為佳，并將結果繪制在同一坐標系下，得到圖5所示的點云圖，其中藍色、紅色區域分別表示主、從機器人工作空間的點云圖。

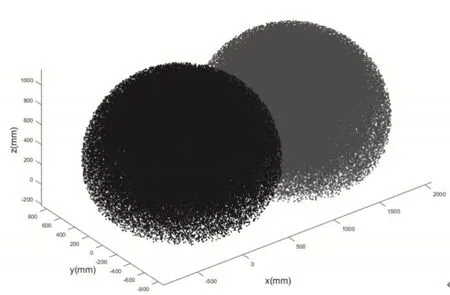
圖5 主、從機器人工作空間點云Fig.5 Point Cloud of Master and Slave Robot Workspace

利用1.3中給出的協作工作空間點云獲取方法，提取上圖的協作區域點云，共尋到69370個點，結果如圖6所示。基于a-Shape算法對協作工作空間進行三維重建，為確定出合適的a值，這里在區間（0，150）內隨機選取了1000組數據，并計算出對應的多面體體積Vi，將結果以坐標（ai，Vi）的形式記錄，結果如圖7所示。

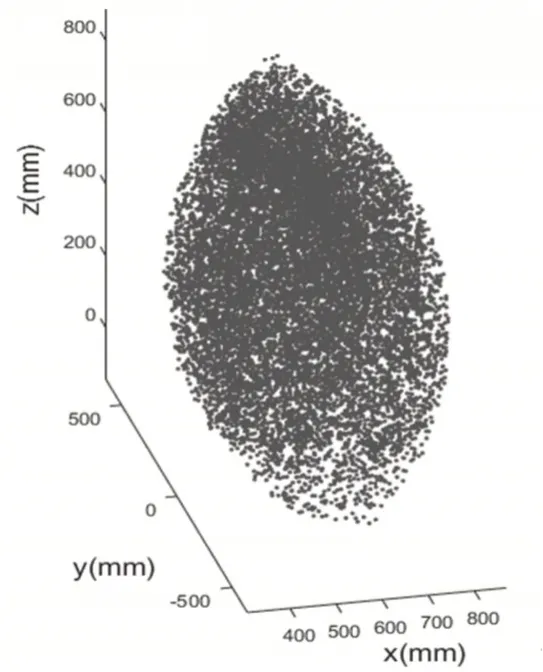
圖6 協作工作空間點云Fig.6 Collaborative Workspace Point Cloud

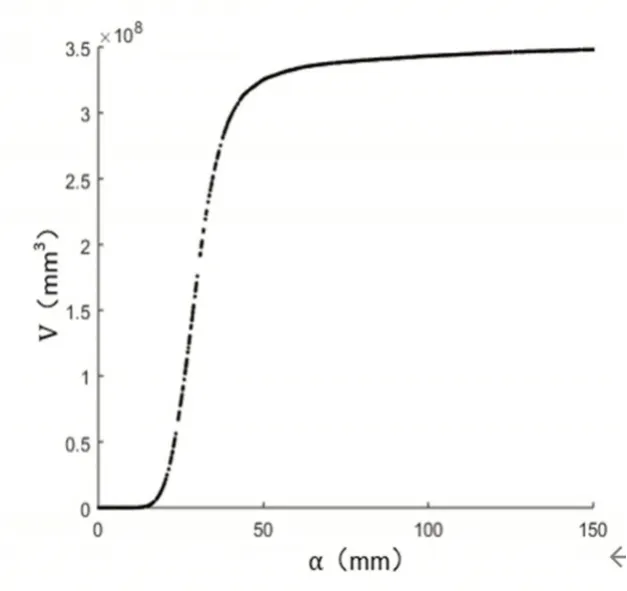
圖7 體積與參數a關系Fig.7 The Relationship between Volume and Parameter a

可以明顯的看到，體積隨著參數a的變化曲線有著較強的連續性和規律性，在a值較小的一段區間內，體積一直為零，這是由于a值過小導致重建的曲面空洞太多，表現為一些離散的三角片，如圖8（a）所示為a=15mm對應的重構結果；當a超過圖中第一個“轉折點”后，體積值發生明顯變化，隨著參數的增加上升趨勢加快，這一過程重建效果逐步完善；當a超過第二個“轉折點”后，曲線明顯變得平緩，體積值基本無變化，表明重建效果已達最佳，再增加a值已經沒有意義，只會保留更多的三角片面。因此，選取本例中第二個轉折點對應的a值為合適的參數，此時a=49.6572mm，計算體積V=0.32493m3，對應的重建結果如圖8（b）所示。為了驗證該方法的重建精度，將協作區域點云與圖8中a=49.6572mm的重建曲面一同繪制，進行對比分析，如圖8（c）所示，可以看到藍色的點云輪廓邊界點均勻分布在曲面上，表明該方法具有較高的精度。

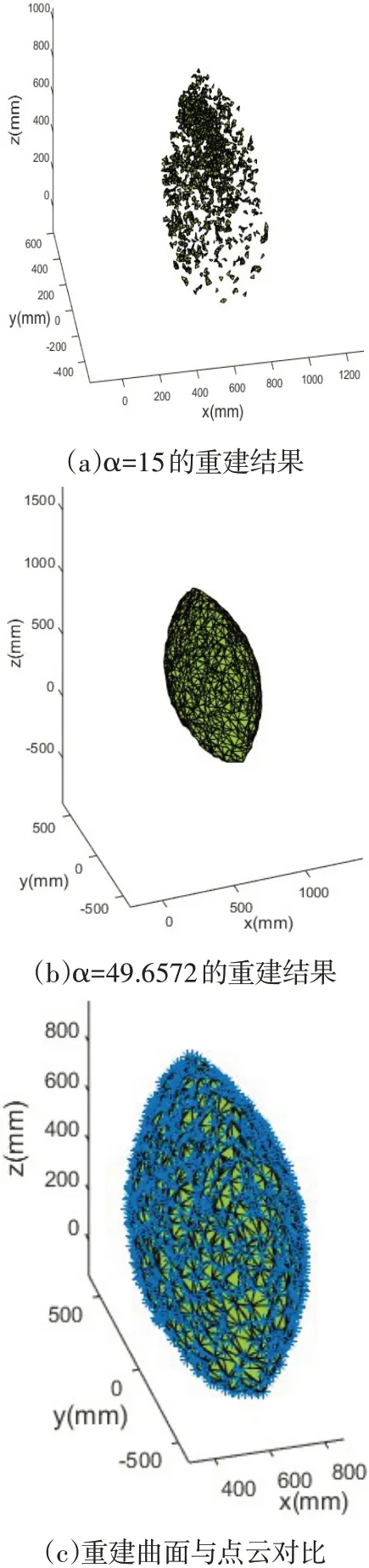
圖8 協作工作空間重建效果Fig.8 Reconstruction Results of Collaborative Workspace

由于主、從機器人型號相同，只對主機器人的工作空間點云進行三維重建，其體積與參數a的關系如圖9（a）所示，確定參數a=44.2570mm，對應體積為2.22039m3，采用該參數的重建結果如圖9（b）所示。為了便于分析，將主、從機器人工作空間和協作工作空間的重建結果相關數據進行整理，如表2所示。

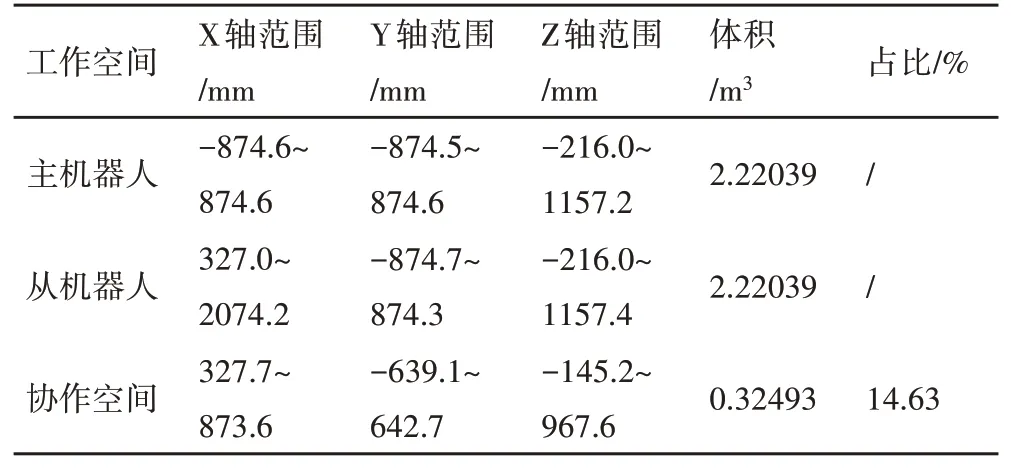
表2 重建結果相關數據Tab.2 Ralated Data of the Reconstruction Results

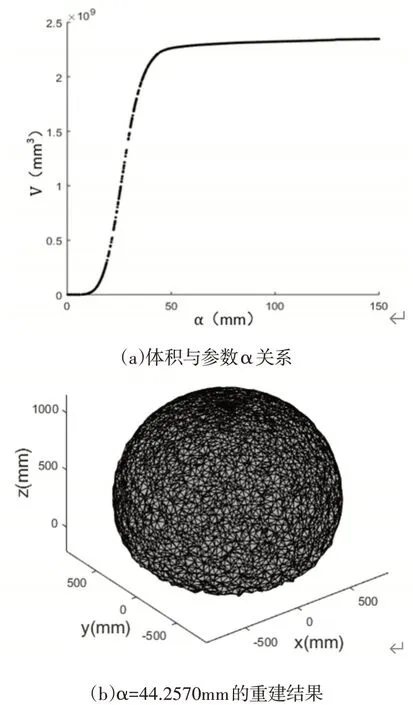
圖9 主機器人工作空間三維重建Fig.9 3D Reconstruction of the Master Robot Workspace

為了驗證volume（）函數對重建多面體體積計算的可靠性，這里以球形工作空間的重建結果體積計算為例，對計算精度進行驗證。隨機點數取3萬，計算結果如表3所示。可以看到，幾種不同半徑的球體采用α-Shape三維重建后，應用volume（）函數計算的體積值誤差均小于1%，說明該方法比較可靠。

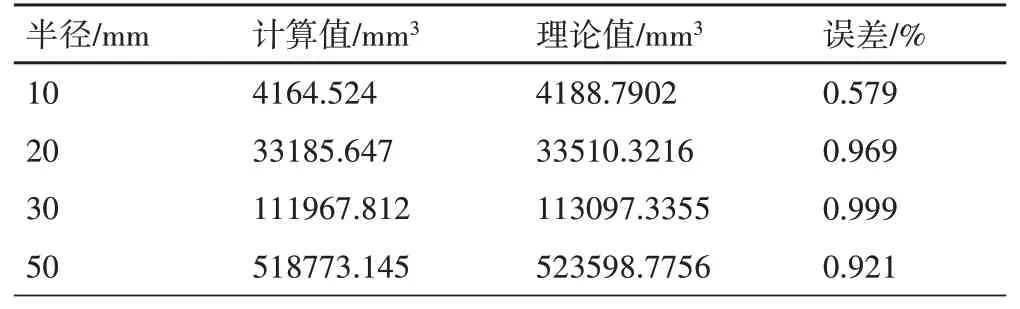
表3 體積計算精度Tab.3 Volumetric Accuracy

工業中，機器人協作完成搬運任務一般對協作工作空間的要求不高，但完成裝配、焊接、涂膠等任務或研究避碰問題時，協作工作空間的相關數據就有著重要的參考意義。例如，采用這里方法可以在協同作業的多臺機器人安裝固定之前，計算得到工作空間與協作工作空間的相關數據，進而結合實際的任務需求判斷機器人布局方式是否滿足要求，避免多次安裝所帶來的額外人力及物力，提高生產效率。本例中，根據工作空間在空間的分布狀況以及協作區域相對整個機器人工作空間的占比，雙機器人相對布局比較利于機器人協作完成一定的裝配任務。

若只將公式（11）中兩臺機器人基坐標系間平移矩陣第一個元素分別設置為600mm和1600mm，不改變兩臺機器人的姿態和其他條件，采用相同的方法計算得到協作工作空間體積分別為1.12236m3和0.05296m3，協作空間體積占比分別為50.55%和2.39%。容易看出，0.6m的布局下協作區域過大，機器人與工具、工件以及機器人與機器人之間容易發生碰撞；1.6m的布局下，協作工作空間體積過小，主、從機器人在該區域作業時關節易出現奇異值而且TCP點不能以多種姿態到達某個點，兩種布局均不滿足要求。

5 結論

通過機器人運動學方程結合蒙特卡羅法得到了主、從機器人工作空間的點云模型；分析了求交集法提取協作空間點的缺點，并給出了通過計算點與點距離并加入一定閾值的判斷方法，有效的提取到了協作區域的點云；為了使工作空間可視化和數字化，提高應用性，這里運用三維重建相關理論，采用a-Shape算法分別對機器人工作空間和協作工作空間進行了重建，以形體的體積計算值作為參考衡量重構效果，給出了基于體積值的參數a確定方法，并得到了較好的重建效果；最后對重建結果的相關數據進行分析，表明該方法對規劃機器人的布局方式具有較強的參考意義，為工業中機器人協作完成各種任務提供一定的理論依據。