局部多粒度覆蓋粗糙集

謝德華，劉財輝，凌 敏

贛南師范大學 數(shù)學與計算機科學學院，江西 贛州 341000

1 研究背景

將經(jīng)典粗糙集理論擴展至多粒度空間下的粗糙集模型[1-2]，在理論研究和實際應(yīng)用上愈加重要，廣泛應(yīng)用于特征選擇、 知識獲取、 決策分析、 模式識別和醫(yī)療診斷等領(lǐng)域[3-6]．因?qū)嶋H問題中數(shù)據(jù)的多樣性，經(jīng)典粗糙集在實際應(yīng)用場景中具有局限性，各類粗糙集擴展模型的研究成為一個研究熱潮，如：決策粗糙集模型、 變精度粗糙集模型、 概率粗糙集模型等[7-9]．文獻[10]研究了多粒度粗糙集模型的代數(shù)結(jié)構(gòu)．文獻[11]對模糊空間下的多粒度粗糙集模型進行了探討．文獻[12]研究了覆蓋空間下的多粒度粗糙集模型，且利用元素的最小描述對不同多粒度覆蓋粗糙集進行比較，發(fā)現(xiàn)了樂觀多粒度和悲觀多粒度與平均多粒度覆蓋粗糙集之間的關(guān)系．文獻[13]提出了基于模糊鄰域多粒度粗糙集的特征選擇算法，從信息的角度提出了基于模糊鄰域熵的不確定性度量．文獻[14]提出了4類基于覆蓋的樂觀(悲觀)多粒度模糊粗糙集模型，引入了模糊互補β-鄰域簇的概念．文獻[15]研究了基于矩陣的動態(tài)優(yōu)勢多粒度粗糙集(DMGRSs)方法，更新了具有演化數(shù)據(jù)的動態(tài)有序信息系統(tǒng)中的多粒度近似．隨著大數(shù)據(jù)的發(fā)展，為了提升精確率，文獻[16-17]提出了局部粗糙集模型，提出了決策理論粗糙集在大數(shù)據(jù)背景下目標概念近似表示的改進，以及局部多粒度決策粗糙集．在局部粗糙集的基礎(chǔ)上，文獻[18]提出了基于不完備信息系統(tǒng)下的局部粗糙集理論，將局部粗糙集從完備信息系統(tǒng)擴展至不完備信息系統(tǒng)．文獻[16-18]的研究都基于等價關(guān)系．文獻[19]基于相容關(guān)系，探討了樂觀多粒度和悲觀多粒度的局部相容粗糙集．文獻[20]研究了相似關(guān)系下的局部粗糙集模型．本文從信息概念和存在概念之間的交叉角度，利用覆蓋粗糙集理論基礎(chǔ)[21-25]，提出了一種在覆蓋近似空間下的局部粗糙集模型：局部覆蓋粗糙集，以及局部樂觀多粒度覆蓋粗糙集和局部悲觀多粒度粗糙集．本文探討了在多粒度空間與單粒度空間下模型的內(nèi)在聯(lián)系，和局部多粒度覆蓋粗糙集的基本性質(zhì)，深入研究了對樂觀多粒度和悲觀多粒度下的局部多粒度覆蓋粗糙集中上、 下近似集的關(guān)系．研究結(jié)果表明，局部多粒度覆蓋粗糙集在特定情況下可退化為多粒度覆蓋粗糙集模型，是對原有模型的有效拓展.

2 理論基礎(chǔ)

近似概念是覆蓋近似空間中的知識表示．文獻[21]提出的多粒度覆蓋粗糙集模型將多粒度的思想引入覆蓋粗糙集模型中，采用一簇覆蓋，提出了一種多粒度覆蓋粗糙集模型．本節(jié)介紹經(jīng)典多粒度覆蓋粗糙集的相關(guān)基礎(chǔ)概念.

2.1 覆蓋粗糙集

定義1[3-4]設(shè)U為論域，C為U的子集簇，如果C中所有的集合均不為空，且有∪C=U，那么稱C為U上的覆蓋.

定義2[3]設(shè)U為論域，C={C1，C2，…，Cn}為論域U上的覆蓋，對于?x∈U，x在覆蓋近似空間〈U，C〉中的最小描述MdC(x)為

MdC(x)={Ci∈C：x∈Ci∧?Cj，且x∈Cj∧S?Ci?Ci=Cj}

(1)

例1給定覆蓋近似空間〈U，C〉，其中U={1，2，3，4，5，6，7，8，9}，C1，C2∈C，C1={{1，2，4，5，7，8}，{2，5，8}，{3，5，6，9}}，C2={{1，2，3}，{4，5，6，7，8}，{7，8，9}}．最小描述和覆蓋的近似集可以由以下計算得到：

根據(jù)定義2有

MdC1(1)=MdC1(4)=MdC1(7)={{1，2，4，5，7，8}}

MdC1(2)=MdC1(8)={{2，5，8}}

MdC1(5)={{2，5，8}，{3，5，6，9}}

MdC1(3)=MdC1(6)=MdC1(9)={{3，5，6，9}}

MdC2(1)=MdC2(2)=MdC2(3)={{1，2，3}}

MdC2(4)=MdC2(5)=MdC2(6)={{4，5，6，7，8}}

MdC2(7)=MdC2(8)={{4，5，6，7，8}，{7，8，9}}

MdC2(9)={{7，8，9}}

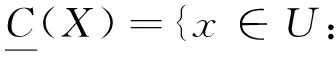
(2)

(3)

該形式下的覆蓋粗糙集將由最大描述和最小描述轉(zhuǎn)化為粗糙集經(jīng)典表示，當覆蓋關(guān)系變成劃分關(guān)系時，覆蓋粗糙集即為經(jīng)典粗糙集.

2.2 局部粗糙集

這里對文獻[16]中提出的局部粗糙集的定義作基本介紹.

定義4令〈U，?〉為偏序集，?是論域中的一種偏序關(guān)系，對任意的x，y∈U，D(y/x)有：

(a) 0≤D(y/x)≤1；

(b)x≤y?D(y/x)=1；

(c)x≤y≤z?D(x/y)≤D(x/z).

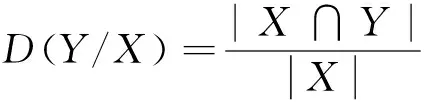
X?Y?D(X/Z)?D(Y/Z)

定義5[16]令(U，R)為一個近似空間，D是定義在P(U)×P(U)上的包含度，P(U)為論域U的冪集，則對任意?X?U，有

(4)

(5)

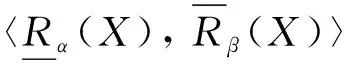
2.3 多粒度覆蓋粗糙集[23-26]

文獻[21]提出的多粒度覆蓋粗糙集模型，結(jié)合多重二元關(guān)系，將多粒度空間引入文獻[10]所提出的覆蓋粗糙集模型中，采用一簇而非單個的覆蓋，提出了一種新的多粒度覆蓋粗糙集模型．以下是相關(guān)的基本介紹：

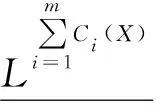
(6)

(7)

由上述結(jié)論可以得到多粒度覆蓋上近似與覆蓋上近似之間的關(guān)系，以及多粒度覆蓋下近似與覆蓋下近似之間的關(guān)系.

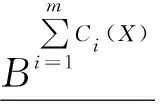
(8)

(9)

定義8[21]設(shè)U為論域，C1={C1，C2，…，Cn}和C2={C1，C2，…，Cm}為論域上的兩個覆蓋．?x?U，若對于?Ci∈MdC1(x)，都存在Cj∈MdC2(x)，使得Cj?Ci，則稱覆蓋C2比覆蓋C1細，記為C2?C1．若C2?C1且C1?C2，則稱覆蓋C2與覆蓋C1相等，記為C2=C1； 否則為不相等，記為C2≠C1．若C2?C1且C2≠C1，則稱覆蓋C2較覆蓋C1嚴格細，記為C2C1.

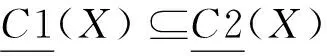
3 局部多粒度覆蓋粗糙集模型

本節(jié)提出一種新的粗糙集擴展模型：局部覆蓋粗糙集．并在此基礎(chǔ)上擴展至多粒度空間，形成多粒度局部覆蓋粗糙集．討論單粒度空間和多粒度空間下的局部覆蓋粗糙集模型及其性質(zhì)，并與覆蓋粗糙集對比且加以說明.

3.1 局部覆蓋粗糙集

定義9在近似空間(U，C)上，令U為論域，C={C1，C2，…，Cn}為該近似空間(論域)的一簇覆蓋，對于?X?U，0≤β<α≤1，X在覆蓋近似空間(U，C)中的局部覆蓋粗糙集的下近似集、 上近似集分別為：

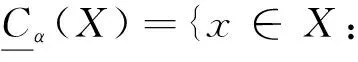
(10)

(11)

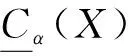
這說明局部覆蓋粗糙集并沒有改變原有覆蓋關(guān)系下的目標近似，與原有的覆蓋粗糙集的近似表示一致.

例2在例1的假設(shè)條件下，令α=0.6，β=0.4，令X={1，2，5，8}，則局部覆蓋粗糙集的上下近似集為：

[1]C1={{1，2，4，5，7，8}} [2]C1={{1，2，4，5，7，8}，{2，5，8}}

[5]C1={{1，2，4，5，7，8}，{2，5，8}，{3，5，6，9}}

[8]C1={{1，2，4，5，7，8}，{2，5，8}}

[1]C2={{1，2，3}} [2]C2={{1，2，3}}

[5]C2={{4，5，6，7，8}} [8]C2={{4，5，6，7，8}，{7，8，9}}

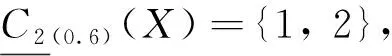
從上述計算結(jié)果看，

這表明對于集合X，其正域有增加，意味著在近似表示上可以更加精確．而對于C2，X在C2的覆蓋粗糙集上是完全不可定義的，但在C2的局部覆蓋粗糙集上可定義，表明對于集合X，局部覆蓋粗糙集在知識近似表示方面是更精準的.

3.2 局部多粒度覆蓋粗糙集

將單個粒度下的局部覆蓋粗糙集擴展至多個粒度空間下得到的局部多粒度覆蓋粗糙集．而在多粒度近似空間中，多粒度覆蓋粗糙集與局部多粒度覆蓋粗糙集的表示見圖1.

圖1 多粒度覆蓋粗糙集與局部多粒度覆蓋粗糙集

其近似集定義表示及其性質(zhì)的分析如下：

定義10在覆蓋近似空間(U，C)上，U為論域，C={C1，C2，…，Cn}為論域上的一簇覆蓋，對于?X?U，0≤β<α≤1，X在覆蓋近似空間(U，C)上的局部樂觀多粒度覆蓋粗糙集的下、 上近似集分別表示為：

(存在Cnj∈MdCn(x)，使得D(X/[x]Cnj)≥α，Cnj?X)}

(12)

(?Cnj∈MdCn(x)，D(X/[x]Cnj)>β，Cnj∩X≠?)}

(13)

定義11在覆蓋近似空間(U，C)上，U為論域，C={C1，C2，…，Cn}為論域上的一簇覆蓋，對于?X?U，0≤β<α≤1，X在覆蓋近似空間(U，C)上的局部悲觀多粒度覆蓋粗糙集的下、 上近似集分別表示為：

(?Cnj∈MdCn(x)，D(X/[x]Cnj)≥α，Cnj?X)}

(14)

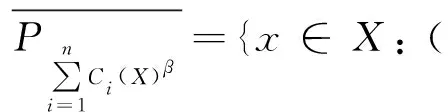
(存在Cnj∈MdCn(x)，使得D(X/[x]Cnj)>β，Cnj∩X≠?)}

(15)

例3在例1的假設(shè)條件下，當X={1，2，5，8}時，根據(jù)定義6可計算覆蓋C的樂觀多粒度覆蓋粗糙集的下近似集與上近似集：

根據(jù)定義10以及例2可得局部樂觀多粒度覆蓋粗糙集的下近似集、 上近似集：

同理可求得悲觀多粒度覆蓋粗糙集的上、 下近似集和局部悲觀多粒度覆蓋粗糙集的上、 下近似集.

定理3設(shè)U為論域，C={C1，C2，…，Cn}為論域上的一簇覆蓋，對于?X?U，0≤β<α≤1，有

證對于?x∈U，由局部多粒度覆蓋粗糙集的下近似集可得：

而對于?x∈U，根據(jù)局部多粒度覆蓋粗糙集的上近似集可得：

證畢.

定理3說明了在覆蓋近似空間中覆蓋關(guān)系下的局部多粒度覆蓋粗糙集的近似集與單粒度下的局部覆蓋粗糙集之間的聯(lián)系．可以清晰地觀察到：局部多粒度覆蓋粗糙集的下近似集是所有單粒度下局部覆蓋粗糙集下近似集的并集； 局部多粒度覆蓋粗糙集的上近似集是所有單粒度下局部覆蓋粗糙集上近似集的交集.

定理4設(shè)U為論域，C={C1，C2，…，Cn}為論域上的一簇覆蓋，對于?X?U，0≤β<α≤1，有：

定理5設(shè)U為論域，C={C1，C2，…，Cn}為論域上的一簇覆蓋，對于?X?U，有：

定理5表明了在特殊情況下，局部多粒度覆蓋粗糙集會退化為多粒度覆蓋粗糙集，以及兩者在覆蓋近似空間上的聯(lián)系.

定理6設(shè)U為論域，C={C1，C2，…，Cn}為論域上的一簇覆蓋，對于?X?U，給定0≤β<α≤1，下列結(jié)論不一定成立：

證見例3．限于篇幅，證明略.

定理6得出一個結(jié)論，即局部多粒度覆蓋粗糙集在覆蓋近似空間上不一定滿足對偶性．換一句話說，全局多粒度覆蓋粗糙集中由下近似集的補，根據(jù)對偶性原理得到的其上近似集，在局部多粒度覆蓋粗糙集中是不一定成立的.

定理7設(shè)U為論域，C={C1，C2，…，Cn}為論域上的一簇覆蓋，若C1?C2?…?Cn，且0≤α1≤α2≤…≤αn，0≤β1≤β2≤…≤βn，則

證因為C1?C2?…?Cn且0≤α1≤α2≤…≤αn，所以根據(jù)定義7和定理1可推得

即

從而根據(jù)定理3有

同理，因為C1?C2?…?Cn且0≤β1≤β2≤…≤βn，根據(jù)定義7和定理1可得

即

根據(jù)定理3可得

證畢.

定理7說明：在給定的一簇覆蓋中存在某種特殊的粗細關(guān)系，使得多粒度局部覆蓋粗糙集的下近似與在最細條件下得到的局部覆蓋粗糙集的下近似相等，多粒度局部覆蓋粗糙集的上近似與在最細條件下得到的局部覆蓋粗糙集的上近似也相等.

定理8設(shè)U為論域，C={C1，C2，…，Cn}為論域上的一簇覆蓋，對于?X?U，給定0≤β<α≤1，有：

證根據(jù)局部樂觀多粒度覆蓋粗糙集和局部悲觀多粒度覆蓋粗糙集的定義，定理8易證.

4 結(jié) 論

當下，多粒度粗糙集在粗糙集理論中的重要性愈加契合現(xiàn)實應(yīng)用場景，新的理論和應(yīng)用拓展可以有效推動粗糙集領(lǐng)域的發(fā)展．本文在覆蓋近似空間下，首先基于覆蓋粗糙集中的最小描述轉(zhuǎn)化后的粗糙集經(jīng)典表示形式，提出了局部覆蓋粗糙集，并研究了在多粒度近似空間下的局部樂觀多粒度覆蓋粗糙集和局部悲觀多粒度覆蓋粗糙集．其次，研究了多粒度空間下的局部覆蓋粗糙集與單粒度局部覆蓋粗糙集間的內(nèi)在聯(lián)系，發(fā)現(xiàn)了局部多粒度覆蓋粗糙集的上、 下近似集跟所有單粒度下局部覆蓋粗糙集的上、 下近似集的代數(shù)關(guān)系．最后，探討了局部多粒度覆蓋粗糙集與多粒度覆蓋粗糙集間的一些基本性質(zhì)，指出了局部多粒度覆蓋粗糙集可在特定情況下由多粒度覆蓋粗糙集泛化得到.