基于PID的溫度控制系統設計

楊 帥,田益民,鄭美俊,高 雪,宋方方

(北京印刷學院信息工程學院,北京 102600)

基于目前轉型后的經濟結構,智能化的溫度控制系統[1]越來越受到人們的推崇,它有著更加突出的優點,比如節省人力、物力,更加安全可靠。在系統工作過程中經常需要測量的一個量便是溫度,需要保持和控制的量也是溫度。

在工業生產過程中,PID[1]控制算法是最常用的控制溫度的方法,PID控制器具有的優點是原理簡單、使用方便、控制精度高、算法成熟,使其成為系統控制的主要技術手段,尤其是對被控對象不是很清楚,又或者被控系統的結構參數必須依靠現場調節或者必須依靠經驗來確定時,就目前來說最適合且最適合的方法便是PID控制。溫度控制系統有許多弊端,如較大的慣性,比較嚴重的滯后性,很難建立較精確的系統數學模型,因此,需要PID控制器加以調節來改善溫度控制系統的性能。

1 PID控制器

自動控制系統[2]的核心便是控制,目前的自動控制技術都是基于反饋理論的概念。反饋理論包括三個部分,即包括測量,比較和執行。對變量進行測量,在期望值做比較,用比較得到的誤差來糾正調節系統的響應。如何更好地對系統進行校正,則成為自動控制技術應用的關鍵。

1.1 PID控制原理

線性連續系統的PID控制系統中包括PID控制器及其被控對象,其原理框圖如圖1所示:

圖1 PID控制系統

線性連續系統的PID控制器是一種比例滯后—超前控制器,它是由比例(P)、積分(I)和微分(D)三個環節組成,再使得三個環節并聯之后,在和系統中的被控對象串聯所構成的一種控制器。PID控制器[3]的形式有P、PI、PD和PID四種結構形式。其中,P為比例控制,PI為比例滯后控制,PD為比例超前控制,PID為比例滯后—超前控制。

比例環節,微分環節,積分環節三者之間的關系如表1所示:

表1 比例環節,微分環節,積分環節對比

1.2 PID控制算法

PID控制器又叫作比例積分微分控制器,它是將比例(P)、積分(I)和微分(D)這三種調節方式組合而成,根據所用到的組合環節不同,所能起到的作用及組合而成的控制器也不盡相同,通過這些不同作用的控制器,便可以應用在相當范圍的各類控制系統中,從而起到控制調節的作用,使得控制系統能達到我們所期望的功能。PID控制器算法及其相關的P(比例)控制器算法和PI(比例積分)控制器算法的表達式如下。

P(比例)控制器算法的線性表達式為:

2 控制系統的時域性能指標

在分析控制系統時,除了要考慮到系統的結構、參數等條件外,一個常用的方法便是通過系統的各項性能指標來分析,當用到系統性能指標有一個前提條件,便是系統必須是穩定系統。如果系統不穩定,則性能指標會計算不出來,會使得研究系統動態響應變得毫無意義。比較常用的系統性能指標[4]有tr(上升時間)、tp(峰值時間)、ts(調節時間)、σ%(最大超調量)、td(延遲時間)、N(振蕩次數)和ess(穩態誤差)。這七個指標都是時域性能指標其中,前六項屬于瞬態性能指標;ess為穩態性能指標。良好的瞬態性能指標,可以使得系統擁有比較好的穩定性和系統響應更加快速;穩態性能指標決定了能否得到一個準確性的系統。

σ%(最大超調量)是指系統的單位階躍響應的最大峰值Cmax與穩定狀態值C(∞)需要滿足一定量的條件,即應滿足以下公式:

σ%一般應滿足在5%～35%之間。對于單調變化的單位階躍響應,系統的最大超調量為0。σ%(最大超調量)代表了系統的相對穩定性。

以上六個性能指標中,最重要且最經常使用的便是ts(調節時間)與σ%(最大超調量)。σ%(最大超調量)與N(振蕩次數)可以反映系統的穩定性能。tr(上升時間)、tp(峰值時間)、ts(調節時間)和td(延遲時間)這四個性能指標可以反映系統的快速性。通過這六個性能指標可以分析出系統的動態響應,同時好的性能指標可以判斷出系統擁有更好的時域性能,好的性能指標決定了一個好的系統。

穩態誤差[5]可以用ess(Steady-State Errors)來表示。穩態誤差用來描述系統的控制精度(控制準確度)。在工業生產中,我們常用到的便是0型系統、Ⅰ型系統和Ⅱ型系統,高于Ⅱ型系統的控制系統一般不常用,型號越高,代表著控制系統的精度就越高,但與此同時該系統的穩定性就會變得越差。

系統在輸入為單位階躍信號,斜坡信號和拋物線信號的作用下的不同類型的系統的穩態誤差如表2所示:

表2 給定輸入下系統的穩態誤差

其中,Kp表示位置誤差系數;Kv代表著速度誤差系數;Ka表示加速度誤差系數。

3 溫度控制系統的設計

溫度控制系統[6]的組成包括調節器、執行機構、被控對象和測量裝置等幾部分組成。溫度控制系統需要滿足的最基本的性能[7]便是快速性。穩定性和準確性。根據需要的精度,選擇不同的控制器,便能夠得到適合的,令人滿意的結果。溫度控制系統流程如圖2所示:

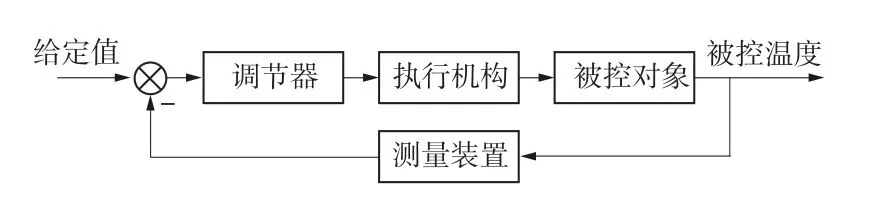
圖2 溫度控制系統結構圖

溫度控制系統模型可以表示為:

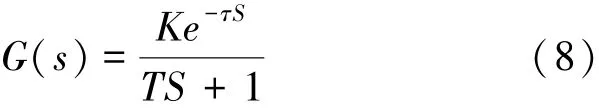
式中,K代表著過程對象的靜態增益,τ表示過程對象的純滯后時間,T代表著過程對象的時間常數。

溫度控制系統進行設計時,我們所采用的控制器為P(比例)控制器,PI(比例積分)控制器,PID(比例積分微分)控制器。

在調節這些控制器的參數時,人們所用的最常見的方法便是經驗法(試湊法),這種方法可以避免使用一些非常復雜的公式,使人們對溫度控制系統的設計節約了時間。Ziegler-Nichols(工程整定法-反應曲線法)是工業生產過程中最常用的控制方法。這種方法便是依靠一些公式和簡單的經驗來確定出比較準確的PID控制器的參數,所以Ziegler-Nichols方法也被稱作經驗公式,由于知道了溫度控制系統的傳遞函數,因此所用到的方法是試湊法和Ziegler-Nichols方法的第二個調整法。Ziegler-Nichols的第二個調整法的經驗公式如表3所示:

表3 Ziegler-Nichols的第二個調整法

表格中的a值,便可以通過直接觀察該溫度控制系統的特性曲線來得到。也可以通過另外一種計算方法得到,這種方法可以被稱為三角比例計算法。三角比例法如圖3所示:

結合圖3,求a和L值的公式為:

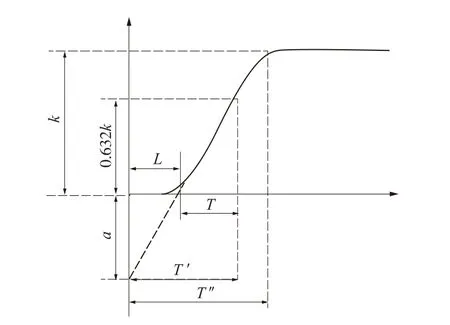
圖3 三角比例法

通過Ziegler-Nichols(工程整定法-反應曲線法),我們便可以得到KP,TI和TD的值,再根據經驗法,增大I(積分)控制器的參數值,達到我們所希望的預定值,再微調D(微分)控制器,直到系統達到所期望的效果。

4 溫度控制系統的設計仿真

恒溫箱[8]在我們日常生活中有著很普遍的使用。通過對恒溫箱溫度控制系統模型的設計,使用PC機操作系統為Windows10,CPU為Intel i5-10200H處理器,運行內存為16G。MATLAB[9]軟件里面的關于Simulink[10]的模塊化編程。

恒溫箱[11]溫度控制系統模型:

在Simulink中建立系統模型,再分別用P(比例)控制器,PI(比例積分)控制器,PID(比例積分微分)控制器加入該系統模型,從而做出對比,分析比較用三種控制器的優缺點。

用Simulink建立該溫度控制系統模型,該系統模型如圖4所示。

圖4 恒溫箱溫控系統模型

通過該系統模型,進行系統分析仿真[12],該系統模型中滯后時間為30s,則應該在Transport Delay模塊[13]中設置參數滯后時間為30s。為方便對比分析,系統輸入模塊給定值應設置為100,仿真結果如圖5所示:

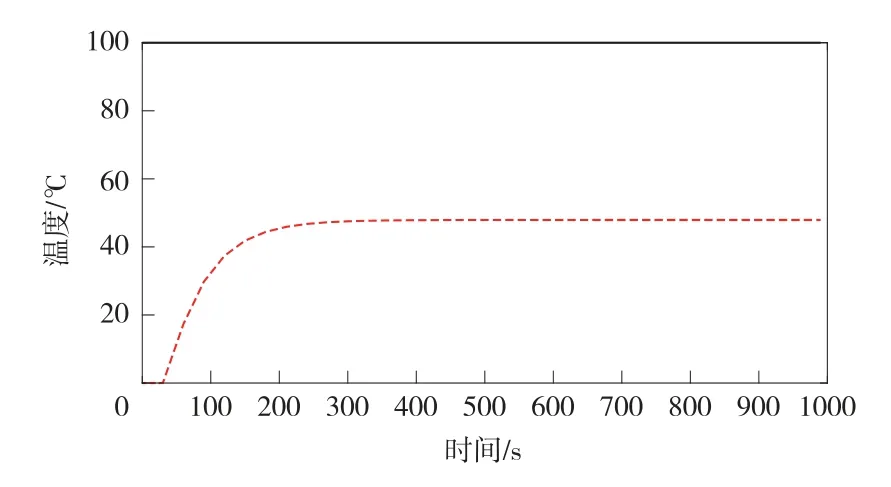
圖5 恒溫箱溫控系統仿真結果

輸入模塊參數給定值為100時,觀察系統的響應曲線可以看出,該系統的穩態誤差居然超過了50%,說明該系統的精度很差,恒溫箱溫控系統系統也不好,必須加入控制器來調節該系統性能。根據這個設計出來的恒溫箱是根本無法使用的,因此我們便對該系統進行改善。

在恒溫箱溫控系統中加入P(比例)控制器,對P控制器參數進行調節設定。系統滯后時間為30秒,系統輸入參數給定值為100,在Simulink設計該系統模型如圖6所示:

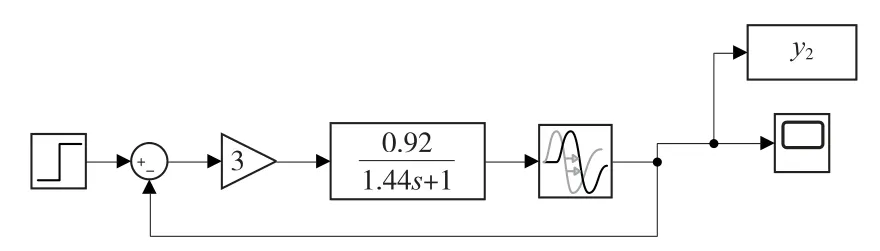
圖6 基于P(比例)控制器恒溫箱溫控系統

該系統的輸出響應曲線如圖7所示:

圖7 加入P控制器的溫控系統輸出響應

通過加入P(比例)控制器后,可以明顯看到,系統的穩態誤差變成了30%以內,說明了系統的精度得到了一定的改善。系統的上升時間也比原來縮短。系統的性能得到了一定的改善。

在恒溫箱溫控系統中加入PI(比例積分)控制器,所建立的系統模型如下圖8所示:

圖8 基于PI控制的溫控系統

在該系統模型中設置參數,KP=3,KI=0.02,滯后時間為30秒,輸入給定初始值為100,得到的系統響應曲線如圖9所示:

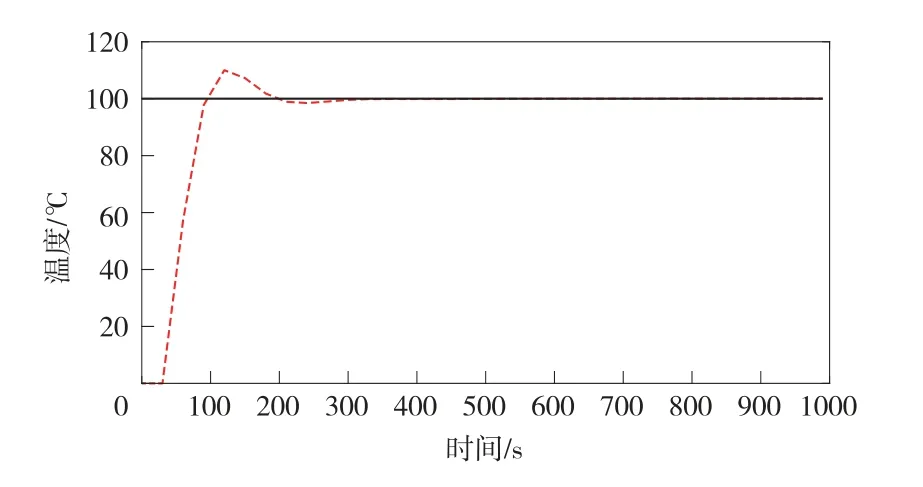
圖9 基于PI控制的溫控系統響應曲線

分析圖5—9得出的響應曲線圖,我們可以看到系統的穩態誤差幾乎是0,系統的精度較高。而且系統的調節時間大大的縮短,約為300秒,系統的超調量,該系統的性能指標較良好。系統的動態性能較之前得到了很大的改善。

使用PID控制器進行溫度控制系統的設計,在Simulink中所建立的系統模型如圖10所示:

圖10 PID校正的溫控系統

在溫控系統中加入PID控制器,通過對PID參數值進行設定,KP=3,KI=0.02,KD=5,其他條件不變,可以得到該系統的響應曲線如圖11所示:

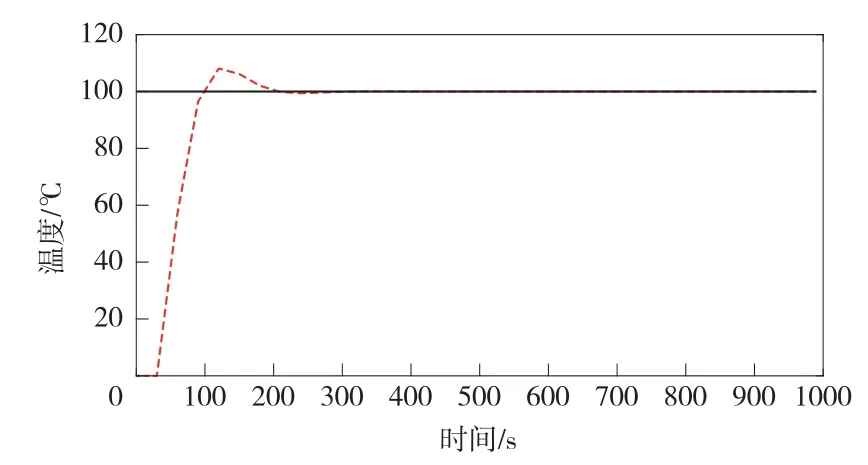
圖11 基于PID的溫控系統響應曲線

該系統中加入PID控制器后,從圖中可以看出,系統的調節時間較之前變小,約為200秒,系統的穩態誤差為0,超調量為10%。該系統的性能指標都良好,系統的精度也高,因此,此時系統的動態性能較之前有了很大的改善。使用PID控制器的效果要優于使用P控制器和PI控制器。

使用PID控制器,當受到外界信號干擾時,更能看出系統性能的優越性,因此,我們在上述模擬系統中加入一個在400秒到430秒之間+50的干擾信號。此時系統模型如下圖12所示:

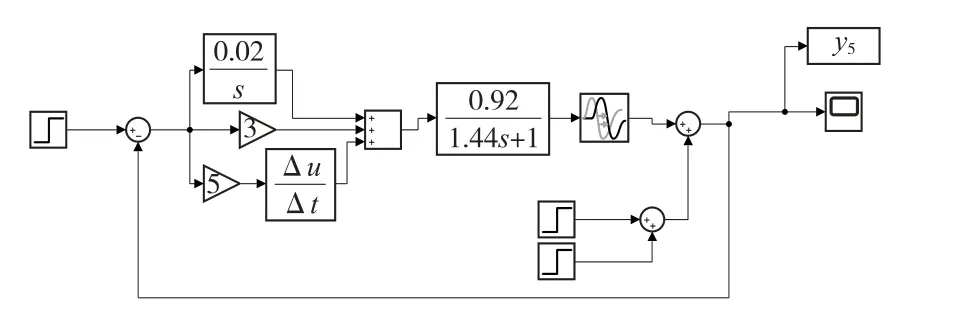
圖12 受干擾的系統模型

該模擬系統的仿真結果如圖13所示:

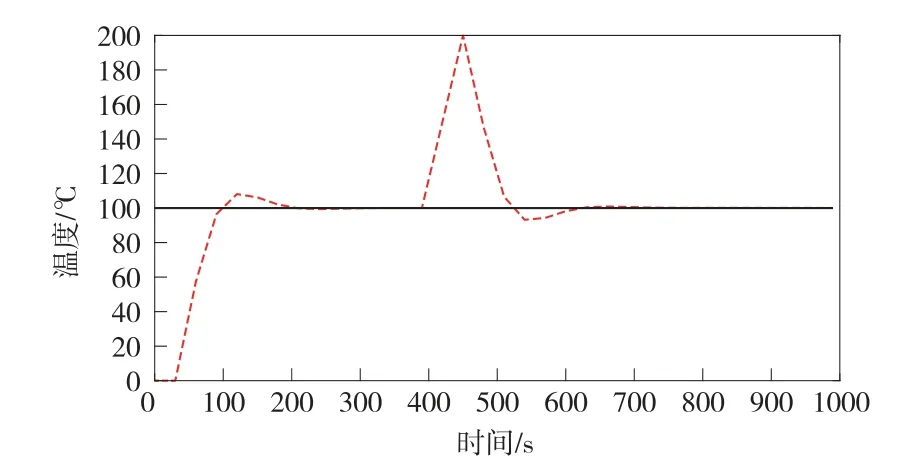
圖13 系統響應仿真曲線

從圖13可以看出,就算系統加入干擾信號,該系統也能較好地抑制這種干擾,具有比較良好的抗干擾能力,并且很快系統再次趨于穩定狀態。因此,更加證明了使用PID控制器的優越性。

5 結語

在系統設計過程中,分別在溫度系統中加入P控制器,PI控制器,PID控制器,通過各自的輸出響應可以看出,基于P的溫度控制系統產生了一定的超調量,系統的穩態誤差也減小。基于PI的溫度控制系統的穩態誤差為0,所用調節時間縮短,約300s。超調量為10%,系統的性能得到了很大的改善。基于PID的溫度控制系統的穩態誤差為0,系統的調節時間比PI控制時更短,約200秒,此時系統的動態特性最好。從輸出響應看出,系統收到干擾信號的影響后能很快恢復到穩定狀態,說明PID控制的溫控系統具有較強的抗干擾能力。