考慮頻率偏差的動態同步相量估計器
李文番 張國鋼 陳沐傈 鐘浩杰 耿英三
(電力設備電氣絕緣國家重點實驗室(西安交通大學)西安 710049)
0 引言
傳統的同步相量測量裝置(Phasor Measurement Unit,PMU)未考慮電信號的幅值、頻率和相位波動,認為電信號是恒定正弦波,通常采用離散傅里葉變換(Discrete Fourier Transform,DFT)及各類改進技術進行相關參數估計[1-2]。實際電力系統中的電壓電流信號的幅值、相位和頻率通常存在一定波動,傳統的基于DFT的同步相量測量技術在電參量存在波動的情況下難以實現對信號同步相量的精確估計。為了實現動態同步相量測量,學者們提出了一系列動態估計算法。
文獻[3]提出一種由插值DFT(Interpolated DFT,IpDFT)與希爾伯特變換(Hilbert Transform,HT)相結合得到的動態同步相量估計算法,并通過穩態和動態測試分析了所提出算法的性能。文獻[4]提出一種高精度相量測量方法,可用于PMU的測試與校準。文獻[5-6]提出了一種用于電力系統振蕩情況下的同步相量測量方法,由于該方法采用泰勒展開公式,因此稱之為泰勒傅里葉變換(Taylor-Fourier Transform,TFT)。TFT打破了傳統DFT只能分析穩態正弦信號的限制,能夠在幅值、相位波動時精確估計待分析信號的動態同步相量。此外,TFT還能夠得到信號的實時頻率和頻率變化率(Rate of Change of Frequency,ROCOF)。在此基礎上,學者們又對TFT做了進一步的改進及拓展應用[7-15]。文獻[7-8]通過設計最大平坦濾波器實現動態同步相量和頻率的測量,在一定程度上增加了所設計的最大平坦濾波器的帶寬,其本質是借助窗函數對TFT進行加權處理,使得分析誤差降低、帶寬增大。TFT的計算過程中需要進行矩陣的求逆、乘法等操作,運算量較大。針對運算量問題,文獻[9]提出一種基于多項式實現的方法,能夠針對某次特定諧波進行參數估計,大大減小了TFT的計算量。文獻[10]將TFT和卡爾曼濾波算法相結合,得到一種運算量小、實時檢測性能強的泰勒卡爾曼濾波器(Taylor-Kalman Filter,TKF)動態諧波測量算法。文獻[11]在TKF的基礎上對其進行了進一步優化,得到一種動態性能更好、測量精度更高、穩定性更好的加強版TKF。文獻[12]利用TFT的動態信號檢測能力,將其用于動態諧波分析,在完成同步相量測量的同時,實現了對各次諧波的動態同步相量的測量。同步相量測量中,間諧波干擾信號會導致TFT算法性能的嚴重下降,文獻[13-14]將壓縮感知(Compressive Sensing,CS)算法和TFT相結合,提出一種能夠分析多頻率信號的壓縮感知TFT多頻模型(Compressive Sensing TFT Multifrequency model,CSTFM),并研究了針對所提出算法減小運算量的方法。文獻[15-16]指出TFT在存在頻偏的情況下,其諧波同步相量的分析精度會下降,且諧波次數越高誤差越大。文獻[15]提出一種基于SINC插值函數的動態同步相量測量算法,其諧波分析帶寬相對于TFT有所增加,但是基波帶寬并未改變。文獻[16]將DFT和TFT相結合,通過查表法實現了寬頻帶同步相量測量,但是計算過程相對復雜,且計算量較大。
隨著動態同步相量測量技術的發展,IEEE關于同步相量測量的相關標準也在逐步完善,從早期未考慮動態變化情況的版本[17]發展到如今考慮動態同步相量[18-19]。根據IEEE標準,電力系統同步相量測量中的最大頻偏可以達到5Hz。所以動態同步相量測量算法需要有較大的帶寬,TFT算法是目前動態同步相量分析中很熱門的研究,但是大多數文獻并未在模型中考慮頻率偏差,算法帶寬并不能達到5Hz,有的文獻能夠達到這一帶寬,但是算法實現較復雜,計算量較大。
本文提出一種考慮頻率偏差的寬頻TFT動態同步相量估計器(Wide Band Taylor-Fourior Transform,WB-TFT),即使頻偏達到5Hz也能保持對同步相量的精確估計,并且與TFT相比較,WB-TFT的在線計算量并未增加。WB-TFT在標稱頻率的兩側以固定的頻率間隔生成多個離散頻率點,然后根據實際標稱頻率和虛擬標稱頻率,利用TFT的方法生成多個動態濾波器,將其保存到存儲器,便于后續查表使用。在線計算時,需要檢測待分析信號的頻偏。為了最大可能降低算法復雜度和運算量,WB-TFT不借助鎖相環、DFT等其他頻率檢測手段,而是使用TFT自身計算得到的頻率,以遞推的方式進行頻偏估計。根據估計頻率選擇與之最接近的離散頻率點對應的濾波器進行同步相量測量。最后,在各種典型的頻率偏差條件下,通過仿真信號和實際信號測試了WB-TFT的性能。測試結果表明,該方法能夠在IEEE標準規定的頻率偏差條件下對動態同步相量進行精確估計。
1 考慮頻偏的動態同步相量估計器
根據IEEE標準C37.118.1[18]及其最新修訂版C37.118.1a[19],電力系統中實際信號的基波頻率偏離系統標稱頻率值的最大值可以達到5Hz,因此,同步相量測量裝置必須具有足夠的帶寬。本文提出一種考慮頻率偏差的動態同步相量估計算法,該算法能夠在最大頻偏達到5Hz的條件下正常工作,并且,與現有的TFT算法相比,在相同的頻偏條件下該算法能夠取得更高的分析精度。
1.1 同步相量估計器數學模型
根據文獻[18-19],電力系統信號的同步相量可以表示為
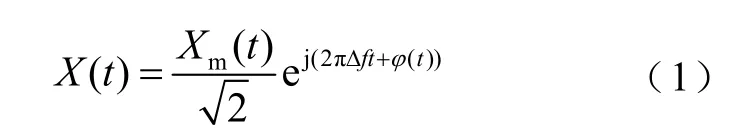
式中,Xm(t)為信號的瞬時幅值;Δf為實際信號頻率與系統標稱頻率之間的偏差;?(t)為信號隨時間變化的初相角。由同步相量可以得到信號的時域模型為

式中,f0為系統標稱頻率;f為信號的實際頻率。
相關文獻介紹的基于TFT的動態同步相量測量算法通常對式(2)做了簡化處理,在分析中忽略了系統頻偏,即默認Δf為零。這樣處理使得問題得到了簡化,并且TFT具有最大平坦濾波器性能,在頻偏較小時TFT的分析精度受影響較小[7-8]。但是,隨著頻偏的增大,TFT的分析誤差迅速增大,所以簡化模型不能在頻偏較大時對電參量進行精確估計。WB-TFT在模型中考慮了Δf,并將式(2)通過歐拉公式變換為

式中,p(t)為輸入信號的動態同步相量,為p(t)的共軛;ω為實際角頻率,ω=2πf。注意,與TFT模型不同,這里使用的是實際信號頻率。動態同步相量p(t)包含了幅值、初相角信息,根據泰勒公式,可以將其在一段觀察時間T內進行K階泰勒展開。

假設采樣周期為Ts,在觀察窗口時間內,t=0的兩側各有Nh個采樣點,總共N=2Nh+1個采樣點。結合式(3)、式(4),并對其進行離散化,可以得到矩陣表達式為
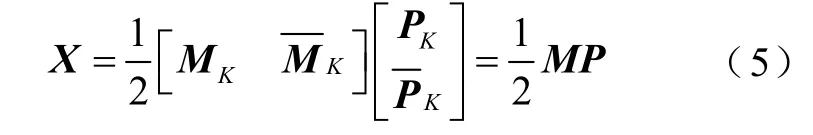
式中,X為在一個觀察窗口內輸入信號的采樣點構成 的 列向量,X= [x(?Nh)…x(0)…x(Nh)]T;MK為N×K的矩陣,為其共軛,其中的列向量可以表示為?Nh≤n≤Nh;PK為同步相量p(t)在t=0時刻的各階導數構成的列向量,PK= [p(0)…p(k)(0)…p(K)(0)]T,為其共軛。
綜上所述,同步相量在中心點處的各階導數可以通過最小二乘法得到。

式中,M?為M的偽逆矩陣。
至此,通過式(4)、式(6)可以得到同步相量的最小二乘解。必須指出,在上述推導中,矩陣M?使用的不是標稱頻率,而是實際頻率f,因此,必須首先對信號頻率進行檢測。
1.2 頻率離散化處理
在TFT計算中,偽逆矩陣M?的行向量相當于最大平坦濾波器的系數。求解偽逆矩陣需要耗費大量的時間,所以,需要提前求解偽逆矩陣,并將其保存到存儲器中,通過使用查表法,這樣可以大幅度縮減在線運算量。需要指出的是,在考慮頻偏時,偽逆矩陣M?的求解過程需要輸入信號的實際頻率信息。也就是說,要想對偽逆矩陣進行線下求解,前提是先估計出信號實際頻率。根據IEEE標準,最大頻偏可以達到5Hz,因此本文引入離散頻率常數df 對標稱頻率兩側5Hz以內的頻率進行離散化,得到離散頻率值fz為
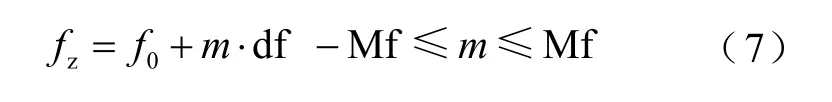
式中,Mf=round(5/df),round()表示四舍五入取整運算符,2Mf+1表示總的離散頻率數量。通過選擇合理的df值,實際信號頻率f和距離它最近的離散頻率之間的差值可以忽略,因此可以用離散頻率代替實際頻率,利用式(5)和式(6)分別生成各個離散頻率點fz對應的偽逆矩陣,并將其保存在存儲器中。上述工作可以離線完成,大大降低在線求解同步相量的運算負擔。在線運行時,首先需要檢測信號的頻率f,并根據這個頻率選擇與之最接近的離散頻率為

1.3 信號頻率估計及WB-TFT的實現流程
常用的頻率檢測方法很多,比如FFT[20]、鎖相環[21-22]等,但是使用這些技術手段必然會額外增加計算量和算法復雜度。TFT在估計同步相量的同時,還可以估計頻率,因此,本文采用TFT本身進行頻率檢測,其具體實現原理詳述如下。
算法啟動時,默認信號頻率為系統標稱頻率,并采用TFT對分析窗口內的信號進行頻率估計,用該估計值作為下一分析窗口的頻率估計值。之后,在每個觀察窗中,將上一個觀察窗中TFT的頻率估計值作為下一個觀察窗的頻率預測值。然后,通過式(8)求出與之最接近的離散頻率,通過查表法選擇與其對應的偽逆矩陣。采用式(4)、式(6)可以求得動態同步相量p(t)及其在窗口中心處的各階導數。進而,輸入信號在窗口中心點處的幅值、相位及其各階導數可表示為(本文以二階泰勒展式為例)

式中,abs(·)表示計算幅值;angle(·)表示計算相位;real(·)表示取實部;imag(·)表示取虛部。
根據泰勒公式可以得到幅值、相位及其導數的時域函數表達式為
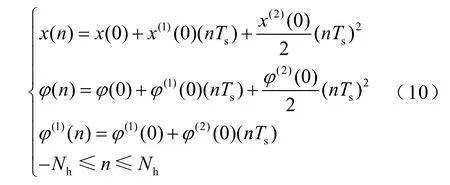
進一步可以求得頻率和頻率變化率為

需要指出的是,在頻率檢測環節,每次使用的頻率預測值是TFT上一個觀察窗口的頻率估計值,所以該預測頻率存在一個觀察窗口的延遲。本文后面的頻率爬坡和系統振蕩仿真證明,該延遲并不會對WB-TFT的分析精度造成很大影響。綜上所述,本文提出的考慮頻偏的同步相量估計器的實現流程如圖1所示。synchrophasor estimator considering frequency deviation
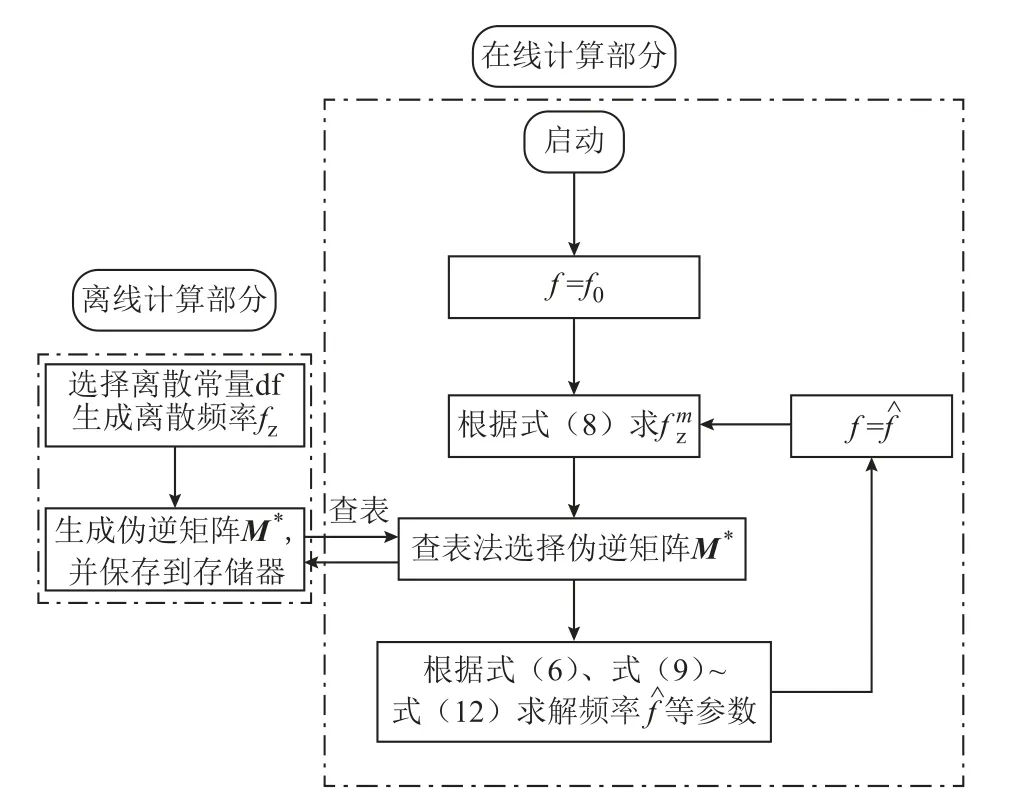
圖1 考慮頻偏的同步相量估計器的實現流程Fig.1 Implementation flowchart of the dynamic
具體實現流程主要包括離線計算和在線計算兩部分,詳述如下:
離線計算部分:
1)選擇合適的離散頻率常數df,生成對應離散頻率fz。
2)根據fz生成對應的偽逆矩陣M?,并將其保存到存儲器中。
在線計算部分:
1)將TFT上一個觀察窗估計得到的頻率值作為本次觀察窗中信號頻率的預測值,并找到與之最接近的離散頻率fz。
2)根據離散頻率選擇相應的偽逆矩陣進行計算,估計出待分析信號的同步相量、頻率和頻率變化率。該頻率估計結果將作為下一個觀察窗的頻率預測值,轉到步驟1)。
2 離散頻率常數選取
本文所提出的估計器模型引入了離散頻率常數df,本部分通過仿真分析離散常數選擇對WB-TFT性能的影響。總矢量誤差(Total Vector Error,TVE)、頻率誤差(Frequency Error,FE)和頻率變化率誤差(Rate of change of Frequency Error,RFE)是IEEE標準中規定的同步相量測量誤差衡量指標,因此在接下來的分析中,誤差分析均根據這些指標進行。
本文采用六個基波周期長度觀察窗,將采樣頻率、TFT階數K、采樣點數N分別設置為3kHz、2、360。離散常數df為0.5Hz、0.2Hz時,最大TVE、FE和RFE的仿真結果如圖2~圖4所示。因為45~55Hz頻率段關于50Hz對稱,所以只給出50~55Hz部分。
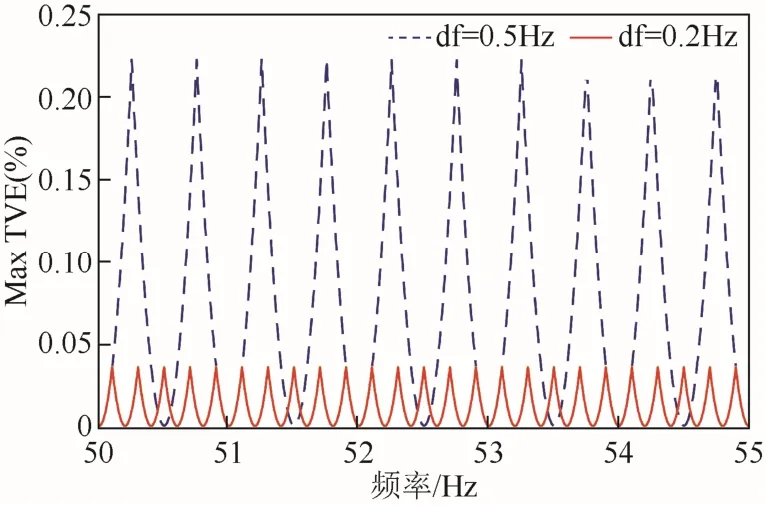
圖2 不同df取值對應的最大TVEFig.2 Max TVE at different df values
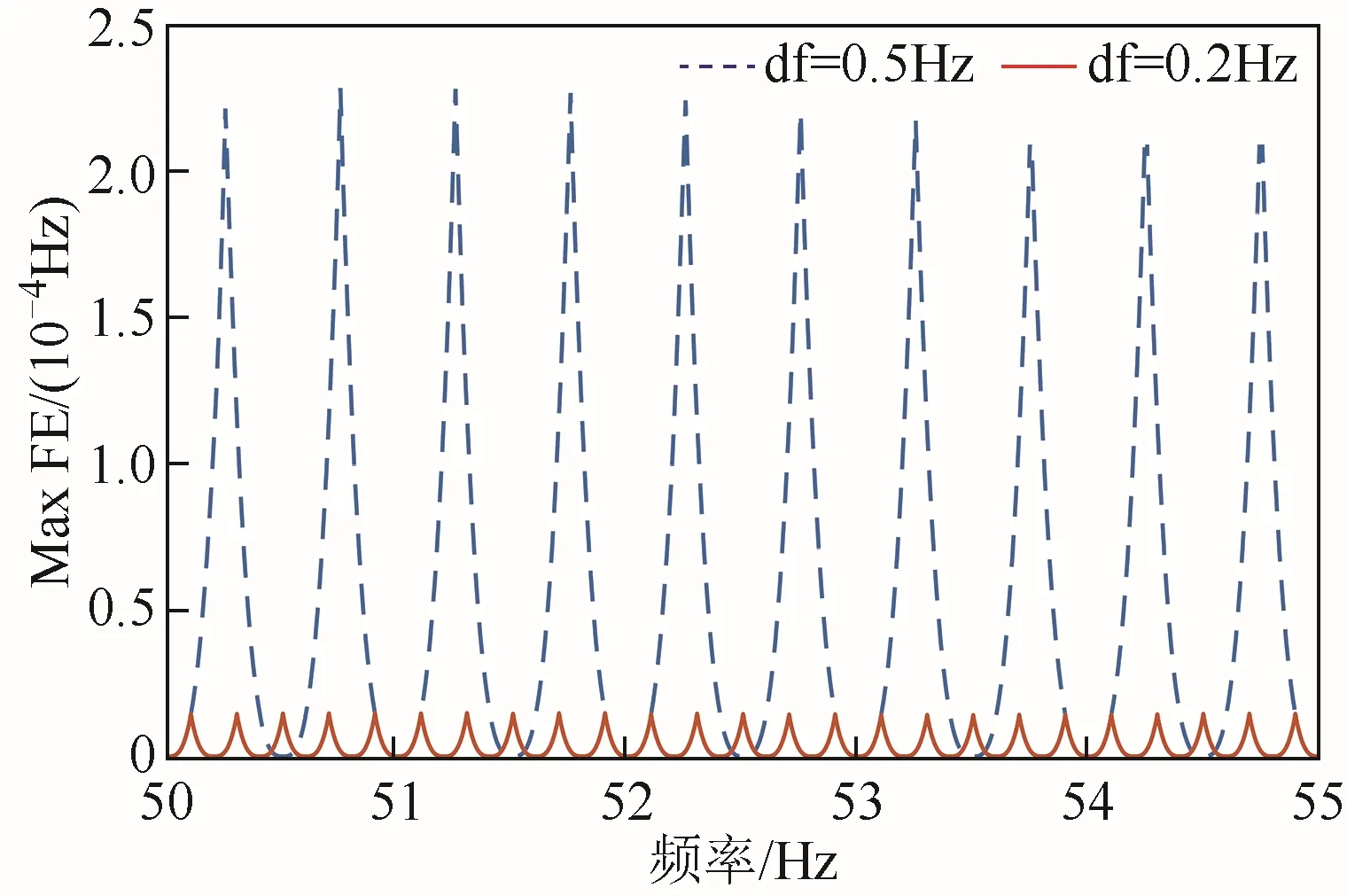
圖3 不同df取值對應的最大FEFig.3 Max FE at different df values
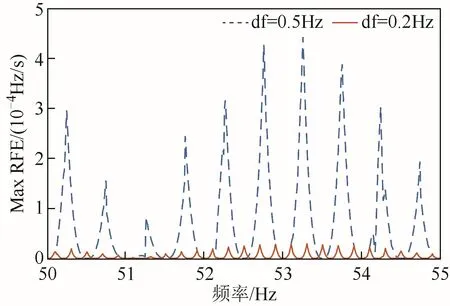
圖4 不同df取值對應的最大RFEFig.4 Max RFE at different df values
從仿真結果可以看出,隨著df的減小,TVE、FE和RFE的值大幅度減小。df越小,離散頻率點越多,需要存儲的偽逆矩陣數量越多,但算法精度越高;反之亦然。通過仿真結果可以發現,當df取不同的值時,各個指標的最大誤差總是出現在兩個相鄰離散頻率點的中心處。比如,由式(7)可得,df=0.5Hz時的離散頻率點集合為{45Hz,45.5Hz,46Hz,…,54Hz,54.5Hz,55Hz},則出現最大誤差的頻率點集合為{45.25Hz,45.75Hz,…,54.25Hz,54.75Hz}。
當df取值為0.54Hz、0.2Hz時頻率預測誤差分別小于0.25mHz、0.02mHz,頻率分析精度完全能夠滿足WB-TFT對信號實際頻率預測的需求。在本文接下來的分析測試中,將df的值選取為0.2Hz。
3 運算量和延遲分析
本文提出的WB-TFT主要包括兩部分內容,即偽逆矩陣的離線計算和同步相量的在線估計。離散頻率常數df越小,離散頻率點越多,對應的偽逆矩陣數量越多。偽逆矩陣系數相當于濾波器,將其離線計算之后保存到存儲器中。如果模型階數為K,采樣點數為N,則每個偽逆矩陣需要3(K+1)行、N列的復數空間進行保存。離線計算不影響在線運算量,所以該算法的主要運算量是由同步相量估計造成的。同步相量估計的計算主要來自式(4)、式(6)、式(10)和式(11),主要的加減和乘除運算量見表1。

表1 WB-TFT的運算量統計Tab.1 WB-TFT calculation statistics
本文將采樣頻率fs、觀察窗采樣數N、模型參數K和df的值分別設置為3kHz,360、2和0.2Hz。由df可以得到在45~55Hz范圍內的離散頻率點數為51,需要離線計算并存儲的偽逆矩陣數量為51個,每個矩陣需要9行、360列的復數空間。按照每個復數占用8個字節計算,總共需要26KB存儲空間。對于實時同步相量估計,由于每次復數運算可以拆分為兩次實數運算,所以需要10 080次實數乘法和10 068次實數加法,即總共20 148次浮點運算。德州儀器(TI)提供的C6000系列浮點處理器TMS320C6712D的時鐘頻率為150MHz,支持256M Byte的存儲空間,并可以執行900 MFLOPS。如果用于計算,則總計算時間將在0.03ms以內,說明WB-TFT的計算量很小。WB-TFT的觀察窗口時間參考點在窗口中心,所以延遲時間為半個窗口長度,即三個基波周期,所以WB-TFT的總延遲時間在60.03ms之內。IEEE標準規定報告率為50幀/s的P類和M類PMU的最大延遲時間分別為40ms和100ms,WB-TFT可以滿足M類PMU的要求,但不滿足P類PMU的要求。
4 綜合性能測試
為了驗證本文WB-TFT算法的綜合性能,本部分進行各種典型工況下算法的性能測試。因為WBTFT是在TFT模型的基礎上考慮了頻偏得到的,下面的測試中用TFT和WB-TFT進行對比。值得注意的是,TFT只能在頻偏很小的時候才有良好的工作性能,當頻偏較大時,TFT性能迅速惡化,WB-TFT能夠工作在頻偏較大的情況下。因此,在以下測試中,使TFT工作在頻偏1Hz以內,WB-TFT工作的最大頻偏達到5Hz。對兩種算法的測試結果進行比較,并與IEEE最新標準要求進行對比,分析WBTFT的綜合性能。IEEE標準將PMU分為兩類:P類和M類。P類PMU要求的響應時間短,而M類PMU要求的測量精度高。在對下面的測試結果進行對比時選擇最嚴厲的方式,即將測量精度與M類裝置比較,響應時間與P類裝置比較。
4.1 頻率爬坡測試
實際電力系統中,系統頻率并非恒定不變,在一定條件下存在頻率爬坡的情況。IEEE標準針對頻率變化情況通常采用頻率線性爬坡的測試方法,即讓系統頻率從標稱頻率開始以某一固定的頻率變化率線性爬坡。頻率爬坡測試信號的表達式為
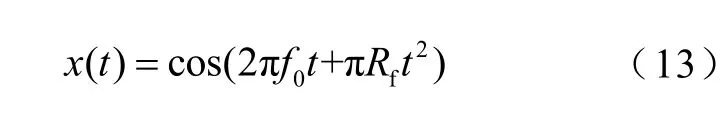
式中,Rf為頻率爬坡率,根據IEEE標準取為1Hz/s。測試中,TFT從50Hz爬坡到51Hz,WB-TFT從50Hz爬坡到55Hz。兩種算法測試得到的TVE、FE和RFE分別如圖5~圖7所示。

圖5 頻率爬坡工況下的TVEFig.5 TVE under frequency ramp condition

圖6 頻率爬坡工況下的FEFig.6 FE under frequency ramp condition

圖7 頻率爬坡工況下的RFEFig.7 RFE under frequency ramp condition
在TFT的爬坡測試中,經過1s時間后,頻率從50Hz爬坡到51Hz,測試得到的TVE、FE和RFE隨著頻率偏差的增大而迅速增大。TVE在t=1.5s左右達到1%,FE在t=1s左右時達到0.015Hz,RFE在t=2s左右時接近0.2Hz/s。
在WB-TFT的爬坡測試中,經過5s時間,頻率從50Hz爬坡到55Hz,頻率偏差最大達到5Hz,但是TVE、FE和RFE分別保持在0.1%、0.002Hz和0.03Hz/s以下,遠低于TFT的測試結果。
IEEE標準規定的頻率爬坡工況下TVE、FE和RFE的約束值分別為1%、0.01Hz和0.2Hz/s。可以看出,WB-TFT的測試結果遠優于TFT,并且能夠滿足標準規定的誤差要求。
4.2 系統振蕩測試
電力系統中的信號不僅存在頻率爬坡,還可能出現頻率和幅值振蕩的情況。IEEE標準通常采用幅值調制和相位調制信號來模擬系統振蕩情況并進行測試,本測試采用的信號為
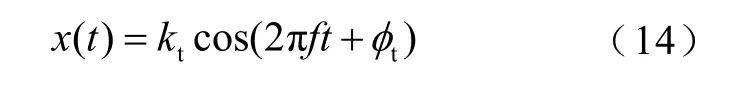
式中,kt為幅值調制因數,kt= 1 +kxc os(2πfmt);φt為相位調制因數,φt=kacos(2πfmt);fm為調制頻率,fm=2Hz;kx和ka為相關系數,kx=ka=0.1;f為包含頻偏的信號頻率,f=f0+Δf。部分頻率下測試得到的誤差結果統計見表2。

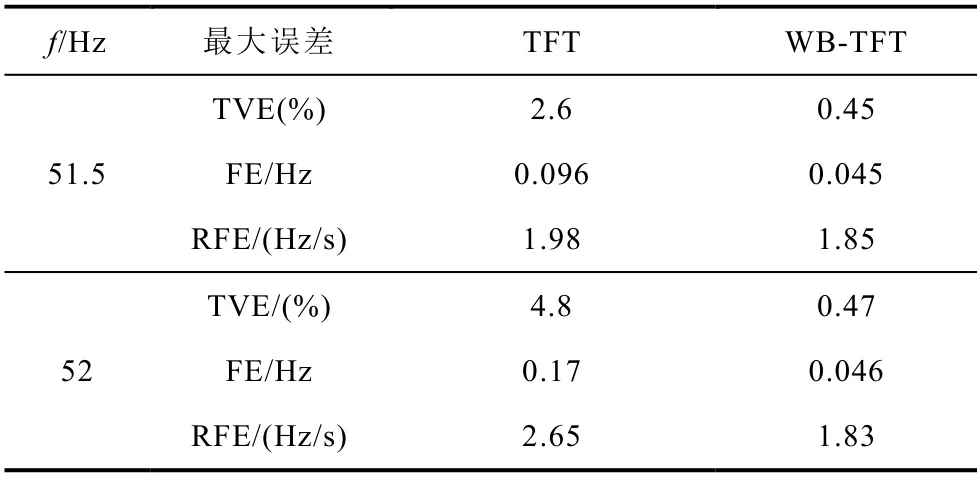
表2 TFT和WB-TFT系統振蕩工況測試結果Tab.2 Test results of TFT and WB-TFT under system oscillation condition
(續)
IEEE標準中,M類設備在系統振蕩工況下的TVE、FE、RFE限值分別為3%、0.06Hz和2Hz/s。從表2中數據可以看出,隨著頻率的增大,TFT的各項誤差迅速增大,并且在51Hz時FE達到標準限值,到52Hz時各項誤差指標均超出標準限值。但WB-TFT的誤差并未隨著頻率增大而出現明顯變化,且TVE、FE、RFE均遠遠小于標準要求值。
在50~55Hz范圍內對TFT和WB-TFT測試得到的TVE、FE、RFE結果如圖8所示。顯然,隨著頻偏增大,TFT的分析誤差迅速增大。在51Hz附近,最大RFE接近標準規定限值,說明在該測試條件下TFT的工作帶寬約為1Hz。WB-TFT的測試誤差波動不大,各誤差值遠小于標準規定限值,其工作帶寬可達到5Hz,即WB-TFT在45~55Hz范圍內的性能能夠滿足標準要求。

圖8 系統振蕩時的TVE、FE、RFEFig.8 TVE、FE、RFE under system oscillation
4.3 諧波和噪聲干擾測試
電力系統中電壓電流信號通常不是純凈的正弦波,而是包含一定諧波分量。根據國家標準GB/T 26862—2011,同步相量測量中通常考慮13次諧波,因此本測試采用的諧波干擾測試信號為

式中,ah為諧波幅值,其取值見表3。IEEE標準對于匯報率Fs>20時TVE和FE的限值為1.3%和0.025Hz,最新的標準取消了對RFE的要求。頻率f= 50Hz 時,WB-TFT的TVE、FE的測試結果如圖9所示。從測試結果可以看出,WB-TFT能夠滿足標準要求。

表3 各次諧波的幅值Tab.3 Amplitude of every harmonic
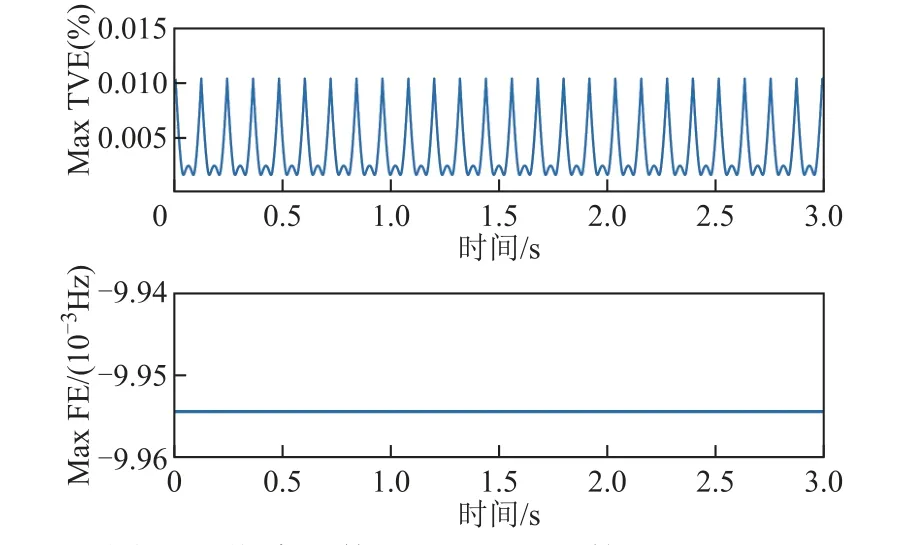
圖9 諧波干擾下WB-TFT的TVE、FEFig.9 TVE、FE of WB-TFT under harmonic disturbance
存在頻偏情況下的TFT和WB-TFT的測試結果見表4。可以看出,隨著頻率偏差的增大,TFT和WB-TFT的誤差均有所增大。51Hz時兩種算法的結果相差不大,當頻率增大到54Hz時,TFT的結果已經完全失去意義,WB-TFT的誤差并未有明顯增大,說明WB-TFT能夠在較大頻偏工況下工作。
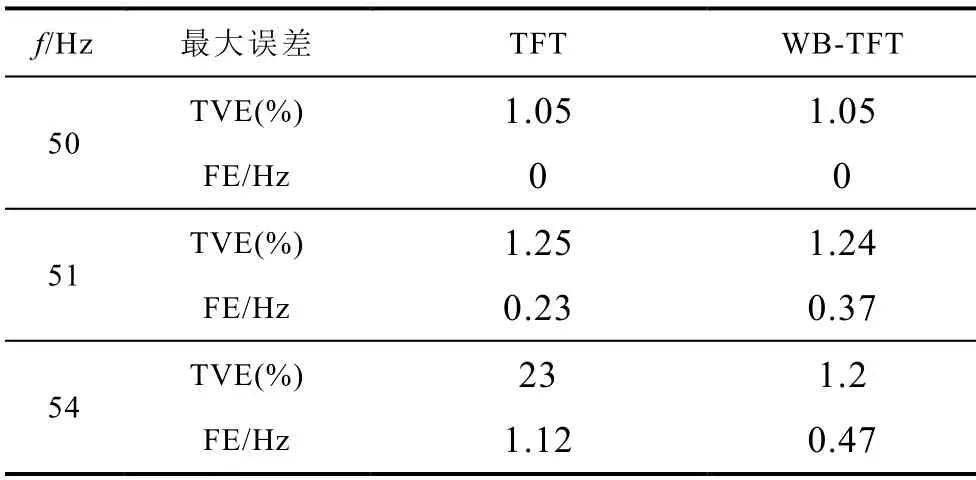
表4 存在頻偏時諧波干擾工況測試結果Tab.4 Test results of harmonic interference in the presence of frequency deviation
4.4 實際信號測試
由于較難采集到頻率偏差較大的實際信號,此處使用某光伏電站采集到的穩態電流數據進行WB-TFT的性能測試。實際電流波形如圖10所示,采集時使用的采樣頻率為10kHz。

圖10 實際電流波形Fig.10 Actual current waveform
文獻[15]提出一種類似于TFT的估計器(簡稱DHSE),并對兩者做了對比。DHSE的具體介紹見附錄。本文所提出的思想同樣可以應用于DHSE,以下將基于DHSE改進得到的考慮頻偏的同步相量估計器簡稱為WB-DHSE。接下來的測試中,使用TFT、WB-TFT和WB-DHSE三種算法對所采集的電流信號進行分析,并對三種算法的分析結果通過作圖的方法加以對比。采樣率都設置為10kHz,采樣點數取1 201,df取0.2Hz,得到的幅值和頻率估計結果如圖11所示。理論上來講,信號頻率偏差較小時TFT和WB-TFT的分析結果應該非常相似。圖11中兩種算法在分析實際電流信號時得到的結果幾乎完全重合,符合理論分析。TFT、WB-TFT和WB-DHSE的幅值分析結果與實際波形幅值基本一致,三者的頻率仿真結果也很接近,說明本文所提出的考慮頻偏的估計器模型可以用于實際信號的電參數估計。
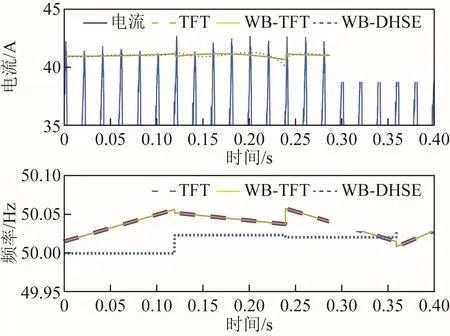
圖11 電流信號幅值和頻率的估計結果Fig.11 Amplitude and frequency estimate results of the current signal
5 結論
本文在TFT動態同步相量估計器的基礎上,提出一種考慮頻率偏差的動態同步相量估計器WBTFT。WB-TFT在TFT的基礎上增加頻率離散化和信號頻率在線檢測兩個部分。WB-TFT引入了一個離散頻率常數df,對基波頻帶進行離散化,并根據離散頻率fz離線計算出對應的偽逆矩陣M?,將其保存到存儲器中。在線計算時,通過TFT完成信號頻率估計,并根據頻率估計值找出與之最接近的離散頻率,進而選擇對應的偽逆矩陣完成同步相量、頻率和頻率變化率的計算。
文章分析了離散頻率常數的選擇對于WB-TFT分析結果的影響,通過仿真對比發現,df取值越小,則需要的存儲空間越大,WB-TFT的計算精度越高,反之亦然。考慮到運算量和模型的復雜度,本文未采用鎖相環、DFT等其他頻率檢測手段,而是直接采用TFT的頻率估計值作為信號的頻率預測值。所提出的模型極大地增加了泰勒傅里葉的帶寬,但沒使用任何外部頻率檢測工具,沒有增加計算負擔。最后,通過各類典型仿真信號和實際采樣數據對WB-TFT的綜合性能進行了測試。測試結果表明WB-TFT能夠在較大頻偏情況下實現同步相量、頻率和頻率變化率的精確分析。
附 錄
根據IEEE相關標準[18-19],電信號的同步相量可以表示為
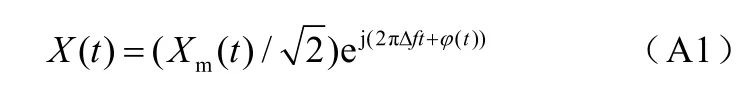
式中,Xm(t)為信號的瞬時幅值;Δf為實際信號頻率與系統標稱頻率之間的偏差;?(t)為信號隨時間變化的初相角。由同步相量可以得到信號的時域模型為
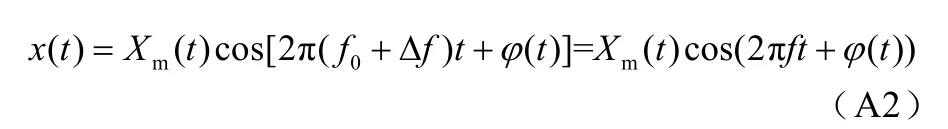
式中,f0為系統標稱頻率;f為信號的實際頻率。對式(A2)進行歐拉公式變換可以得到
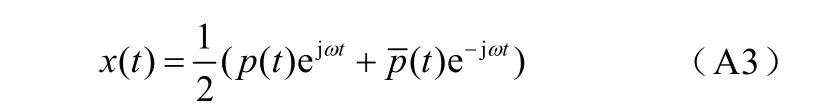
式中,p(t)為輸入信號的動態同步相量,p(t)=Xm(t)ej?(t);ω= 2πf為實際角頻率。動態同步相量p(t)包含了幅值、初相角信息,可以將其在一段觀察時間T內展開為[15]

式中,B0為大于p(t)的最大頻率的一個頻率值;pk為p(t)在t=k/(2B0)時刻以2B0采樣率得到的采樣點,pk=p[k/(2B0)];K為p(0)兩邊的采樣數。觀察窗口的長度需要滿足T<K/B0。
假設采樣周期為Ts,在觀察窗口時間內,時間0點兩側各有Nh個采樣點,總共N=2Nh+1個采樣點。可以得到輸入信號的離散表達式為

進一步可以將其轉換為矩陣表達式,即

式中,M?為M的偽逆矩陣。
令K=2,得到p(t)在觀察窗中心點處的各階導數為

結合式(A8)和式(A4)就可以計算出同步相量p(t)。
令D0=pK(0),D1=pK(1)(0),D2=pK(2)(0),可以得到頻率和頻率變化率的表達式為

和WB-TFT一樣,在上述推導中,偽逆矩陣M?的計算中使用的不是標稱頻率,而是實際頻率f,因此,需要對信號頻率進行檢測。

