基于CPU-GPU異構(gòu)的電力系統(tǒng)靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法

李 雪 張琳瑋 姜 濤 陳厚合 李國(guó)慶

（東北電力大學(xué)電氣工程學(xué)院 吉林 132012）

0 引言

交直流電網(wǎng)互聯(lián)規(guī)模不斷擴(kuò)大、可再生能源大規(guī)模并網(wǎng)，在改善電網(wǎng)大規(guī)模電能輸送能力和優(yōu)化電源結(jié)構(gòu)的同時(shí)，也使電力系統(tǒng)運(yùn)行中隨機(jī)性和不確定性因素日益增加，給電力系統(tǒng)電壓穩(wěn)定性帶來諸多挑戰(zhàn)[1-5]。因此，研究各種隨機(jī)性和不確定性因素影響下的電力系統(tǒng)電壓穩(wěn)定性對(duì)電力系統(tǒng)安全穩(wěn)定運(yùn)行具有極其重要的意義[6-9]。

靜態(tài)電壓穩(wěn)定域（Static Voltage Stability Region,SVSR）是分析和評(píng)估電力系統(tǒng)電壓穩(wěn)定性的重要工具[10-13]，它已在研究強(qiáng)隨機(jī)性和不確定性因素影響下的電力系統(tǒng)電壓穩(wěn)定性中發(fā)揮了巨大的作用，但構(gòu)建SVSR關(guān)鍵在于對(duì)其邊界的搜索。超平面近似作為目前最為通用的靜態(tài)電壓穩(wěn)定域邊界（Static Voltage Stability Region Boundary,SVSRB）構(gòu)建方法，已在工程中得到了應(yīng)用[14-16]。該方法核心思想是在功率注入空間內(nèi)搜索系統(tǒng)所有可能運(yùn)行方式下的鞍結(jié)分岔（Saddle Node Bifurcation,SNB）點(diǎn)，借助這些SNB點(diǎn)來近似SVSRB。因此，構(gòu)建SVSRB關(guān)鍵是對(duì)SNB點(diǎn)的快速、準(zhǔn)確搜索。

目前，電力系統(tǒng)SNB點(diǎn)的搜索方式主要有連續(xù)潮流（Continuation Power Flow,CPF）法[17-18]、最優(yōu)潮流（Optional Power Flow,OPF）法[19]和直接法[20-21]。CPF法以系統(tǒng)當(dāng)前運(yùn)行點(diǎn)為始點(diǎn)，沿指定功率增長(zhǎng)方向采用預(yù)測(cè)-校正方式追蹤系統(tǒng)SNB點(diǎn)，該方法雖可獲得較高精度的SNB點(diǎn)，但系統(tǒng)規(guī)模會(huì)嚴(yán)重制約該方法的計(jì)算效率。OPF法以系統(tǒng)負(fù)荷裕度最大為目標(biāo)函數(shù)、潮流方程為約束條件，通過求解該優(yōu)化模型獲得電力系統(tǒng)的SNB點(diǎn)，但優(yōu)化算法需要通過尋優(yōu)以逐次逼近最優(yōu)解，其求解過程相對(duì)耗時(shí)，且“維數(shù)災(zāi)”問題難以解決，不利于區(qū)域互聯(lián)電力系統(tǒng)SNB點(diǎn)的快速搜索。直接法通過求解一組表征SNB點(diǎn)特性的非線性方程組來搜索SNB點(diǎn)，該方法對(duì)初值較為敏感且計(jì)算量較大，系統(tǒng)規(guī)模的擴(kuò)大會(huì)導(dǎo)致該方法的計(jì)算量和存儲(chǔ)空間急劇增加，故該方法也難以適用于大規(guī)模區(qū)域互聯(lián)電力系統(tǒng)SNB點(diǎn)的快速搜索。為提高SVSRB的搜索效率，文獻(xiàn)[22-23]分別提出了基于邊界追蹤的預(yù)測(cè)-校正算法和基于邊界追蹤的優(yōu)化算法，以實(shí)現(xiàn)SVSRB的快速構(gòu)建。但如何在實(shí)現(xiàn)區(qū)域互聯(lián)電力系統(tǒng)SVSRB高精度構(gòu)建前提下，進(jìn)一步提高SVSRB的計(jì)算效率仍具有十分重要的研究?jī)r(jià)值。

相對(duì)于CPF法和OPF法，直接法通過求解一組表征SNB點(diǎn)特性的非線性方程組便可獲取系統(tǒng)的SNB點(diǎn)，該方法計(jì)算原理簡(jiǎn)單、計(jì)算精度高，且在求解SNB點(diǎn)時(shí)涉及大量的線性方程組計(jì)算，雖然其方程組的計(jì)算量和計(jì)算復(fù)雜度較高，但易于通過GPU并行加速以提高SVSRB計(jì)算效率[24]。因此，本文以直接法為基礎(chǔ)，提出一種基于CPU-GPU異構(gòu)的電力系統(tǒng)靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法。該方法依據(jù)SVSRB拓?fù)湫再|(zhì)，采用沿邊界追蹤SVSRB的搜索方式，將已求SNB點(diǎn)處系統(tǒng)信息作為直接法搜索相鄰SNB點(diǎn)的初值，以克服直接法對(duì)初值敏感的不足；再結(jié)合CPU-GPU異構(gòu)平臺(tái)實(shí)現(xiàn)SNB點(diǎn)的并行求解，以降低直接法計(jì)算量大、計(jì)算復(fù)雜度高的缺陷，從而提升SVSRB搜索效率；最后通過多組測(cè)試系統(tǒng)算例，對(duì)所提SVSRB并行計(jì)算方法的準(zhǔn)確性和有效性進(jìn)行分析、驗(yàn)證。

1 基于直接法的鞍結(jié)分岔點(diǎn)計(jì)算方法

由文獻(xiàn)[25-27]可知，電力系統(tǒng)的SVSRB主要是由SNB點(diǎn)和極限誘導(dǎo)分岔（Limit Induced Bifurcation,LIB）點(diǎn)構(gòu)成的，而LIB點(diǎn)可在SNB點(diǎn)搜索的基礎(chǔ)上，利用參考文獻(xiàn)[28]來判斷是否到達(dá)，因此，SNB點(diǎn)的搜索至關(guān)重要。本文在構(gòu)建SVSRB時(shí)重點(diǎn)關(guān)注SNB點(diǎn)的搜索，將SVSRB的搜索等效為搜索系統(tǒng)在各種可能運(yùn)行方式下的SNB點(diǎn)。而直接法作為一種求解SNB點(diǎn)的常用方法，其原理簡(jiǎn)單，便于計(jì)算，已被用于電力系統(tǒng)SNB點(diǎn)的求解[20-21,28]。因此，本文采用直接法來搜索電力系統(tǒng)的SNB點(diǎn)。

1.1 直接法基本原理

直接法搜索電力系統(tǒng)SNB點(diǎn)的核心思想就是求解一組能夠反映系統(tǒng)SNB點(diǎn)特性的非線性方程組，該非線性方程組的表達(dá)式為

式中，f(x,λ)=0為含參數(shù)的潮流方程，x為狀態(tài)變量，l為負(fù)荷裕度；fx(x,λ)·r=0為潮流方程所對(duì)應(yīng)Jacobi矩陣發(fā)生奇異的方程，fx(x,l)為潮流Jacobi矩陣，r為零特征值所對(duì)應(yīng)的右特征向量，其維度與潮流方程一致；rp-1=0為規(guī)范化方程，rp代表r中的第p個(gè)元素。對(duì)于一給定電力網(wǎng)絡(luò)，若系統(tǒng)總節(jié)點(diǎn)數(shù)為N，PQ節(jié)點(diǎn)共npq個(gè)，PV節(jié)點(diǎn)共npv個(gè)，令n=2npq+npv，則上述非線性方程組的維度為2n+1。

采用直接法求解電力系統(tǒng)SNB點(diǎn)的過程，實(shí)質(zhì)就是采用牛拉法求解式（1）所示的非線性方程組，其求解過程中的修正方程組為

式中，fxxr∈Rn×n，其任意第l行、第d列的元素可表示為，其第p個(gè)元素為1，其余元素均為0；fλ∈Rn為含參數(shù)的潮流方程對(duì)λ的偏導(dǎo)數(shù)。

由式（2）可求得修正量Δx、Δr和Δl，將所得修正量代入式（3）更新變量x、r和l。

設(shè)定收斂閾值ε，將式（3）更新后的x、l和r代入式（1），若滿足收斂條件‖f(x,l)‖≤ε和‖fxr‖≤ε，則迭代完成，SNB點(diǎn)處x、r和l求解完畢；否則，繼續(xù)迭代，直至f(x,l)和fxr滿足上述收斂條件為止。

1.2 修正方程組的降階處理

由式（2）可知：修正方程組式（2）的維數(shù)是潮流方程維數(shù)的兩倍，在迭代求解過程中，計(jì)算量較大，導(dǎo)致整個(gè)SNB點(diǎn)的求解耗時(shí)較高。為降低式（2）中修正量求解的復(fù)雜度和計(jì)算量，文獻(xiàn)[20]將式（2）所示的2n+1維修正方程組通過換元變換拆分成式（4）～ 式（7）所示的四組同系數(shù)n+1維線性方程組。

各修正量與α、β、ξ和η關(guān)系為

式中，Δxp為薄弱節(jié)點(diǎn)電壓幅值變化量，用于臨界點(diǎn)處x、r和l的初值預(yù)測(cè)，其計(jì)算公式為

通過求解降階后的線性方程組式（4）～式（7），并根據(jù)式（8）所示各修正量與α、β、ξ和η的關(guān)系，先求解修正量Δx、Δr和Δl，然后將Δx、Δr和Δl代入式（3），可對(duì)待求變量x、r和l進(jìn)行修正，以提高修正量求解效率，減少數(shù)據(jù)所需存儲(chǔ)空間，提高直接法搜索SNB點(diǎn)的計(jì)算效率。

2 基于直接法的SVSRB并行計(jì)算

采用第1節(jié)所述的直接法在功率注入空間內(nèi)搜索大量SNB點(diǎn)，并借助這些SNB點(diǎn)即可近似系統(tǒng)SVSRB。然而，直接法對(duì)初值非常敏感，若采用傳統(tǒng)的SVSRB搜索方法（簡(jiǎn)稱“射線法”），不當(dāng)?shù)某踔颠x取可能導(dǎo)致直接法求解結(jié)果不收斂或收斂耗時(shí)較長(zhǎng)。同時(shí)，系統(tǒng)規(guī)模的擴(kuò)大將導(dǎo)致直接法的計(jì)算量急劇增加，不利于大規(guī)模電力系統(tǒng)SVSRB的快速搜索。針對(duì)上述不足，本文提出一種基于邊界追蹤的直接法以實(shí)現(xiàn)SVSRB的并行計(jì)算。

2.1 基于邊界追蹤的直接法

邊界追蹤法的核心思想是利用SVSRB上相鄰SNB點(diǎn)的系統(tǒng)運(yùn)行信息變化較小這一特點(diǎn)，將已求SNB點(diǎn)的狀態(tài)量x、右特征向量r和負(fù)荷裕度l作為下一相鄰待求解SNB點(diǎn)的初值，以充分利用各SNB點(diǎn)信息，提高SVSRB構(gòu)建效率。基于該思想，本文將直接法與邊界追蹤法相結(jié)合，提出一種基于邊界追蹤的SVSRB快速搜索的直接法，以有效利用各SNB點(diǎn)的系統(tǒng)運(yùn)行信息，克服直接法初值選取困難的不足。由于基于邊界追蹤的直接法可以很好地保證求解SNB點(diǎn)時(shí)給定初值的精度，因此，有利于加快直接法計(jì)算SNB點(diǎn)的收斂速度，提高SVSRB的搜索效率。

圖1給出了基于邊界追蹤的直接法搜索SVSRB的基本原理。首先給定初始功率增長(zhǎng)方向d0，d0對(duì)應(yīng)的功率增長(zhǎng)方向角q0=arctan(ΔPj0/ΔPi0)，ΔPi0、ΔPj0分別為d0中對(duì)應(yīng)于節(jié)點(diǎn)i、j的功率注入增長(zhǎng)分量。以基態(tài)為起始點(diǎn)，根據(jù)近似二次曲線預(yù)估SNB點(diǎn)初值[20]，采用第1節(jié)所述的直接法計(jì)算功率增長(zhǎng)方向d0下的SNB點(diǎn)0，SNB點(diǎn)0處的狀態(tài)變量、負(fù)荷裕度和右特征向量分別為x0、l0和r0。改變d0中節(jié)點(diǎn)i、j的有功注入增長(zhǎng)分量ΔPi0和ΔPj0，得到新功率增長(zhǎng)方向d1為

圖1 基于邊界追蹤的SVSRB搜索示意圖Fig.1 Exploring SVSRB using boundary tracking method

2.2 直接法并行計(jì)算SVSRB的預(yù)處理

采用邊界追蹤的直接法很好地解決了直接法搜索電力系統(tǒng)SNB點(diǎn)時(shí)初值選取困難這一瓶頸。然而，直接法求解SNB點(diǎn)時(shí)，牛頓迭代修正方程組式（2）的維數(shù)是潮流方程組維數(shù)的兩倍，計(jì)算量大、計(jì)算復(fù)雜度高，嚴(yán)重影響了SVSRB構(gòu)建效率。盡管對(duì)修正方程組式（2）的降階處理有效降低了修正方程組維數(shù)，但降階處理使得需要求解的線性方程組數(shù)量增多，搜索SNB點(diǎn)的計(jì)算量依然很大，不利于SNB點(diǎn)的快速搜索。為此，本文基于CPU-GPU異構(gòu)平臺(tái)，將直接法求解式（4）～式（7）的四組n+1維線性方程組采用帶Jacobi+ILU(0)兩階段預(yù)處理的穩(wěn)定雙共軛梯度法（BICGSTAB）進(jìn)行求解，并借助GPU對(duì)該求解過程進(jìn)行并行加速，以降低直接法搜索電力系統(tǒng)SNB點(diǎn)的計(jì)算量和復(fù)雜度，提高SVSRB搜索效率。

利用GPU的并行計(jì)算能力加速迭代法求解線性方程組是GPU的主要應(yīng)用之一[29-31]，借助GPU的并行計(jì)算優(yōu)勢(shì)，并根據(jù)系數(shù)矩陣B既不對(duì)稱也不正定，且具有高度稀疏性的特點(diǎn)，參考文獻(xiàn)[24]，本文采用Jacobi預(yù)處理與ILU(0)預(yù)處理相結(jié)合的Jacobi+ILU(0)兩階段預(yù)處理方法，并結(jié)合BICGSTAB迭代法求解線性方程組式（4）～式（7），以提高修正量求解速度。

以式（4）為例，本節(jié)簡(jiǎn)要介紹Jacobi+ILU(0)預(yù)處理的BICGSTAB迭代法求解過程。將線性方程組式（4）簡(jiǎn)記為

式中，B為系數(shù)矩陣；α為待求向量；b為等式右側(cè)列向量。對(duì)式（12）進(jìn)行Jacobi+ILU(0)預(yù)處理，處理后的線性方程組等效為

式中，J為Jacobi預(yù)處理矩陣；L、U分別為ILU(0)分解得到的上、下三角稀疏矩陣。選取L為預(yù)處理矩陣，對(duì)式（13）進(jìn)行變換，得到

2.3 基于直接法的SVSRB并行計(jì)算流程實(shí)現(xiàn)

采用基于BICGSTAB迭代法和Jacobi+ILU(0)兩階段預(yù)處理的線性方程組求解方法可以加快式（4）～式（7）的求解效率。為進(jìn)一步提升直接法搜索SNB點(diǎn)的計(jì)算效率，本文采用CPU-GPU異構(gòu)平臺(tái)，將直接法搜索SNB點(diǎn)過程中計(jì)算量較大、計(jì)算耗時(shí)占比高的修正量求解部分由GPU完成，即借助GPU的并行加速技術(shù)對(duì)BICGSTAB迭代法進(jìn)行加速求解，以提高修正量的求解效率，而其他邏輯性較強(qiáng)，計(jì)算量較小部分由CPU完成。具體而言，在CPU中，通過牛拉法對(duì)表征SNB點(diǎn)特性的非線性方程組式（1）線性化處理，得到相應(yīng)的修正方程組式（2），并對(duì)式（2）進(jìn)行降階處理，得到如式（4）～式（7）所示的四組同系數(shù)線性方程組；然后將系數(shù)矩陣B、線性方程組（4）～式（7）右側(cè)列向量、生成的預(yù)處理器J、L和U，以及其他相關(guān)參數(shù)從CPU移植到GPU中，在GPU中，采用帶Jacobi+ILU(0)兩階段預(yù)處理的BICGSTAB迭代法對(duì)式（4）～式（7）進(jìn)行并行求解，得到α、β、ξ和η；接著將α、β、ξ和η傳輸?shù)紺PU中，在CPU中，利用各修正量與α、β、ξ和η的關(guān)系，由式（8）得到修正量Δx、Δr和Δl，并按式（3）對(duì)待求量x、r和l進(jìn)行修正，將修正后的x、l和r代入式（1），重復(fù)牛頓迭代過程，直到f(x,l)和fxr滿足‖f(x,l)‖≤ε和‖fxr‖≤ε，則迭代完成，x、r和l求解完畢，至此，則可實(shí)現(xiàn)SNB點(diǎn)并行求解，從而提高SVSRB的搜索效率。

圖2進(jìn)一步給出了二維有功注入空間內(nèi)所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算的流程。

圖2中采用CPU-GPU異構(gòu)平臺(tái)計(jì)算SNB點(diǎn)的具體過程如前所述，牛頓迭代求解SNB點(diǎn)的初值x0、l0和r0由SVSRB上相鄰已求SNB點(diǎn)的系統(tǒng)運(yùn)行信息給定。因SVSRB上相鄰SNB點(diǎn)距離較近，系統(tǒng)運(yùn)行信息變化較小，故采用基于邊界追蹤的直接法可以保證直接法搜索SNB時(shí)對(duì)初值的高質(zhì)量選取，有利于加快直接法搜索SNB點(diǎn)的收斂速度，克服直接法初值不易選取的不足；而對(duì)于直接法計(jì)算量大、計(jì)算復(fù)雜度高這一缺陷，采用CPU-GPU異構(gòu)平臺(tái)，利用GPU并行技術(shù)對(duì)直接法搜索SNB點(diǎn)時(shí)計(jì)算量較大的四組同系數(shù)線性方程組式（4）～式（7）進(jìn)行并行加速求解，大幅降低了直接法搜索SNB點(diǎn)的計(jì)算量與計(jì)算復(fù)雜度。上述兩種處理方式的有機(jī)結(jié)合，有效解決了直接法初值敏感、計(jì)算量大這兩大不足，實(shí)現(xiàn)了SVSRB上各SNB點(diǎn)的快速并行求解。

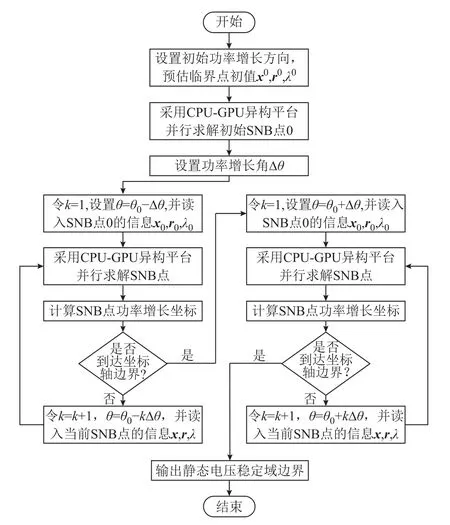
圖2 基于CPU-GPU異構(gòu)的SVSRB并行計(jì)算流程Fig.2 Flow chart of the proposed CPU-GPU heterogeneous computing method

在搜索出SVSRB基礎(chǔ)上，為進(jìn)一步獲取SVSRB近似解析表達(dá)式，以指導(dǎo)電網(wǎng)運(yùn)行人員進(jìn)行電壓穩(wěn)定性評(píng)估與控制，可參考文獻(xiàn)[25]，再對(duì)SVSRB進(jìn)行近似，得到SVSRB的近似解析表達(dá)式。

3 算例分析

針對(duì)所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法，本節(jié)首先以WECC3機(jī)9節(jié)點(diǎn)系統(tǒng)為例，驗(yàn)證本文所提方法的準(zhǔn)確性；然后以歐洲13659節(jié)點(diǎn)系統(tǒng)為例，驗(yàn)證所提方法構(gòu)建區(qū)域互聯(lián)電力系統(tǒng) SVSRB 的可行性；最后以case2737sop、case3120sp、case7092、case9241pegase等多個(gè)測(cè)試系統(tǒng)為例，驗(yàn)證所提方法的有效性。

本文算例計(jì)算硬件平臺(tái)為 Dell PowerEdge C4130機(jī)架式服務(wù)器，CPU為Inter Xeon E5-2690，主頻2.6GHz，內(nèi)存256GB，GPU為Nvidia Tesla K80，總內(nèi)存帶寬480GB/s。軟件平臺(tái)為Matlab2018a，CUDA驅(qū)動(dòng)版本為8.0。構(gòu)建SVSRB時(shí)控制搜索方向的功率增長(zhǎng)角Δq為0.1rad，牛頓-拉夫遜法的收斂精度ε取10-2，最大迭代次數(shù)N取50，BICGSTAB迭代法的收斂閾值εb取10-2。

3.1 WECC3機(jī)9節(jié)點(diǎn)測(cè)試系統(tǒng)

本節(jié)首先以WECC3機(jī)9節(jié)點(diǎn)系統(tǒng)為例[32]，采用所提SVSRB并行計(jì)算方法，分別構(gòu)建二維、三維有功功率注入空間內(nèi)的SVSRB。

3.1.1 二維SVSRB構(gòu)建

選擇節(jié)點(diǎn)5、7的有功注入量為坐標(biāo)軸，在以節(jié)點(diǎn)5、7形成的二維負(fù)荷有功注入空間內(nèi)采用本文所提方法構(gòu)建SVSRB，如圖3所示。

圖3 WECC-9系統(tǒng)的SVSRBFig.3 SVSRB of WECC-9 test system

由圖3可知：首先，以基態(tài)為起始點(diǎn)，設(shè)置追蹤第一個(gè)SNB點(diǎn)時(shí)所對(duì)應(yīng)的功率增長(zhǎng)方向d8=[0 0.326 0 0.170 0 0 0.180 0 0 0.200 0 0 0]T，d8對(duì)應(yīng)的功率增長(zhǎng)方向角q8=0.732 8rad，采用CPUGPU異構(gòu)平臺(tái)并行求解d8下的SNB點(diǎn)。具體過程如下：通過牛拉法對(duì)式（1）線性化處理并對(duì)牛頓迭代修正方程組式（2）進(jìn)行降階處理，得到式（4）～式（7）；然后，將系數(shù)矩陣B、線性方程組式（4）～式（7）右側(cè)列向量、預(yù)處理器J、L和U，以及其他相關(guān)參數(shù)從CPU移植到GPU中，并利用GPU的并行加速技術(shù)，采用帶兩階段預(yù)處理的BICGSTAB迭代法并行求解式（4）～式（7），得到中間變量α、β、ξ和η；再將求解的α、β、ξ和η傳輸?shù)紺PU中，利用各修正量與α、β、ξ和η的關(guān)系得到修正量Δx、Δr和Δl，并按式（3）對(duì)待求量x、r和l進(jìn)行更新；重復(fù)上述過程，直到滿足牛頓迭代收斂條件，則d8下的SNB點(diǎn)并行求解完畢，得到的初始SNB點(diǎn)如圖3中SNB點(diǎn)8所示，其坐標(biāo)為（2.388 0,2.149 2），最大負(fù)荷裕度l8=11.939 8(pu)。

然后，沿q減小方向采用基于邊界追蹤的直接法并行搜索系統(tǒng)SNB點(diǎn)，詳細(xì)過程如下：以SNB點(diǎn)8為起始點(diǎn)，令q7=q8-Δq，根據(jù)d8中節(jié)點(diǎn)5、7的有功增長(zhǎng)分量ΔP5、ΔP7及q7得到新的功率增長(zhǎng)方向d7=[0 0.326 0 0.170 0 0 0.159 1 0 0.217 0 0 0]T；以SNB點(diǎn)8的狀態(tài)變量x8、負(fù)荷裕度l8及右特征向量r8作為直接法搜索d7下SNB點(diǎn)的初值，采用CPU-GPU異構(gòu)平臺(tái)實(shí)現(xiàn)SNB點(diǎn)的并行求解，得到d7對(duì)應(yīng)的SNB點(diǎn)7，SNB點(diǎn)7的坐標(biāo)為（2.661 2,1.951 8），最大負(fù)荷裕度l7=12.265 4(pu)。以此類推，將已求SNB點(diǎn)作為相鄰待求解SNB點(diǎn)的起始點(diǎn)，其狀態(tài)變量、負(fù)荷裕度和右特征向量作為直接法搜索相鄰待求解SNB點(diǎn)的初值，并結(jié)合CPU-GPU異構(gòu)平臺(tái)實(shí)現(xiàn)SNB點(diǎn)的并行求解，依次得到SNB點(diǎn)6,5,4,…,0，其中SNB點(diǎn)0的功率增長(zhǎng)方向角q0=-0.067 2rad，此時(shí)q0＜0，令q0=0，計(jì)算d0=[0 0.326 0 0.170 0 0 0 0 0.269 1 0 0]T下的SNB點(diǎn)0，并停止沿q減小方向SNB點(diǎn)的搜索。

進(jìn)一步，仍以SNB點(diǎn)8為起始點(diǎn)，類似上述過程，沿q增大的方向采用CPU-GPU異構(gòu)的直接法依次搜索SNB點(diǎn)9,10,11,…,17，SNB點(diǎn)17的功率增長(zhǎng)方向角為q17=1.632 8rad，此時(shí)有：q17＞π/2，令q17=π/2，計(jì)算d17=[0 0.326 0 0.170 0 0 0.269 1 0 0 0 0]T下的SNB點(diǎn)17，至此，系統(tǒng)在第一象限內(nèi)沿q增大方向的SΝΒ點(diǎn)搜索結(jié)束。各SΝΒ點(diǎn)詳細(xì)信息見表1。將圖3搜索得到的SΝΒ點(diǎn)依次連接，即可獲得由節(jié)點(diǎn)5、7形成的二維有功注入空間內(nèi)的SVSRB。

表1 WECC-9系統(tǒng)中各SNB點(diǎn)信息Tab.1 Detailed information of SNB of WECC-9 test system

圖3進(jìn)一步對(duì)比了本文所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法與CPF法、基于射線的直接法、基于邊界追蹤的直接法所構(gòu)建的SVSRB。由圖3可知：對(duì)于同一個(gè)功率增長(zhǎng)方向，本文提出的SVSRB并行計(jì)算方法獲得的SNB點(diǎn)和CPF、基于射線的直接法、基于邊界追蹤的直接法得到的SNB點(diǎn)近似重合，有效驗(yàn)證了所提的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法的準(zhǔn)確性。

由于SNB點(diǎn)處潮流方程所對(duì)應(yīng)的Jacobi矩陣發(fā)生奇異，Jacobi矩陣存在零特征值，故搜索得到的SNB點(diǎn)處Jacobi矩陣對(duì)應(yīng)的最小特征值到0的距離可以作為衡量各種方法計(jì)算精度的標(biāo)準(zhǔn)。

圖4分別對(duì)比了CPF、基于射線的直接法、基于邊界追蹤的直接法和本文所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法得到的SNB點(diǎn)處潮流Jacobi矩陣所對(duì)應(yīng)的最小特征值。由圖4中各SNB點(diǎn)處的最小特征值可以看出：本文所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法與基于射線的直接法、基于邊界追蹤的直接法計(jì)算得到的SNB點(diǎn)精度較CPF法搜索的SNB點(diǎn)精度高。圖4中由CPF法所得的SNB點(diǎn)平均最小特征值為1.04×10-2，而本文所提方法與基于邊界追蹤的直接法、基于射線的直接法獲得的最小特征值的平均值分別為1.21×10-3、1.20×10-3、2.01×10-3，該三種方法計(jì)算得到的SNB點(diǎn)精度大致相等，且比CPF的計(jì)算精度高出一個(gè)數(shù)量級(jí)，該對(duì)比結(jié)果表明：本文所提靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法具有較高的計(jì)算精度。

圖4 SVSRB的計(jì)算誤差Fig.4 Calculation errors of SVSRB

進(jìn)一步，在圖3搜索所得SVSRB基礎(chǔ)上，參考文獻(xiàn)[25]，對(duì)圖3的SVSRB進(jìn)行近似，近似結(jié)果如圖5所示，對(duì)應(yīng)的SVSRB局部近似邊界H1、H2、H3、H4、H5、H6、H7、H8解析表達(dá)式如式（16）所示。

圖5 WECC-9系統(tǒng)二維SVSRB的近似邊界Fig.5 Approximated 2-dimensional SVSRB of WECC-9 test case

3.1.2 計(jì)算效率分析

本節(jié)進(jìn)一步對(duì)比了CPF法、基于射線的直接法、基于邊界追蹤的直接法與本文所提方法在上述場(chǎng)景下的計(jì)算效率。

表2給出了上述場(chǎng)景下不同方法構(gòu)建二維SVSRB的計(jì)算時(shí)間。由表2可知，CPF在上述場(chǎng)景下的計(jì)算耗時(shí)遠(yuǎn)大于基于射線的直接法、基于邊界追蹤的直接法和本文所提出方法的計(jì)算耗時(shí)；基于邊界追蹤的直接法在上述場(chǎng)景中的計(jì)算耗時(shí)較基于射線的直接法、CPF法分別減少了24.8%和94.7%；本文所提方法的計(jì)算時(shí)間較基于邊界追蹤的直接法、基于射線的直接法耗時(shí)更長(zhǎng)。出現(xiàn)上述結(jié)果的原因是：CPF法獲得SNB點(diǎn)時(shí)涉及大量的預(yù)測(cè)-校正過程，該過程相對(duì)耗時(shí)，且隨著SNB點(diǎn)數(shù)量的增多，CPF的耗時(shí)明顯增加，因而基于CPF的SVSRB構(gòu)建方法用時(shí)較長(zhǎng)；而本文所提方法與基于射線的直接法、基于邊界追蹤的直接法均是對(duì)表征SNB點(diǎn)特性的非線性方程組進(jìn)行求解，獲得SNB點(diǎn)的過程相對(duì)簡(jiǎn)單，且所需的牛頓迭代次數(shù)遠(yuǎn)小于CPF法校正步的總迭代次數(shù)，因而計(jì)算時(shí)間較CPF更短；但因測(cè)試系統(tǒng)較小，CPU與GPU數(shù)據(jù)交互的耗時(shí)遠(yuǎn)大于GPU并行求解帶來的加速性，因而本文所提方法較基于邊界追蹤的直接法、基于射線的直接法耗時(shí)更久。

表2 不同方法的計(jì)算時(shí)間對(duì)比Tab.2 Computational times compared with different methods

由于直接法搜索電力系統(tǒng)SNB點(diǎn)的核心是利用牛拉法對(duì)式（1）進(jìn)行求解，因此，構(gòu)建SVSRB的計(jì)算耗時(shí)主要依賴于獲取SNB點(diǎn)時(shí)的牛拉法總迭代次數(shù)。表3對(duì)比了本文所提方法與基于射線的直接法、基于邊界追蹤的直接法搜索SVSRB的迭代次數(shù)。

表3 不同方法的迭代次數(shù)Tab.3 Total times of iterations compared with different methods

由表3的對(duì)比結(jié)果可知：基于邊界追蹤的直接法搜索SVSRB時(shí)所需的總迭代次數(shù)較少，因而搜索SVSRB時(shí)計(jì)算耗時(shí)較少；基于射線的直接法搜索SVSRB所需總迭代次數(shù)較多，計(jì)算耗時(shí)較基于邊界追蹤的直接法更長(zhǎng)；而本文所提方法雖有較少的迭代次數(shù)，但構(gòu)建SVSRB所需的計(jì)算時(shí)間比基于射線的直接法和基于邊界追蹤的直接法更久。其主要原因是：基于射線的直接法始終以基態(tài)為起始點(diǎn)，各SNB點(diǎn)的搜索相對(duì)獨(dú)立，且需不斷利用負(fù)荷參數(shù)二階導(dǎo)數(shù)預(yù)估不同功率增長(zhǎng)方向下的SNB點(diǎn)的初值，因此獲得SNB點(diǎn)收斂解所需的牛頓迭代次數(shù)較多，收斂耗時(shí)較長(zhǎng)；而基于邊界追蹤的直接法將已求SNB點(diǎn)作為相鄰待求解SNB點(diǎn)的初始點(diǎn)，因初值更接近待求解SNB點(diǎn)的真實(shí)值，故獲取SNB點(diǎn)時(shí)所需的迭代次數(shù)更少，構(gòu)建SVSRB的計(jì)算耗時(shí)更短；本文所提方法是在基于邊界追蹤的直接法基礎(chǔ)上利用CPU-GPU異構(gòu)平臺(tái)進(jìn)行的SVSRB并行計(jì)算，因而牛頓總迭代次數(shù)較少，但本文采用CPU-GPU異構(gòu)平臺(tái)求解SNB點(diǎn)時(shí)，由于測(cè)試系統(tǒng)規(guī)模較小，CPU與GPU間數(shù)據(jù)交互耗時(shí)遠(yuǎn)大于GPU并行加速的計(jì)算耗時(shí)，因而構(gòu)建SVSRB計(jì)算時(shí)間相對(duì)較長(zhǎng)。

3.1.3 功率增長(zhǎng)角Δq的分析

由于SVSRB上獲得各SNB點(diǎn)的功率增長(zhǎng)方向受功率增長(zhǎng)角Δθ的影響，Δθ過大或過小均會(huì)影響SVSRB的構(gòu)建精度及構(gòu)建速度。因此，本節(jié)進(jìn)一步分析了Δθ對(duì)構(gòu)建SVSRB的具體影響。

表4為不同Δθ時(shí)，在上述坐標(biāo)空間中構(gòu)建二維SVSRB所需計(jì)算耗時(shí)與牛拉法總迭代次數(shù)的對(duì)比。由表4可知：當(dāng)Δθ＝0.05rad時(shí)，構(gòu)建SVSRB所需的SNB點(diǎn)數(shù)量較多，故構(gòu)建SVSRB時(shí)牛頓迭代的總迭代次數(shù)較多，計(jì)算耗時(shí)較長(zhǎng)，但因相鄰SNB點(diǎn)距離較近，因此平均迭代次數(shù)相對(duì)較少；當(dāng)Δθ＝0.25rad時(shí)，構(gòu)建SVSRB所需SNB點(diǎn)數(shù)量較少，故牛頓迭代法的總迭代次數(shù)相對(duì)較少，搜索SVSRB的計(jì)算耗時(shí)較短，但因相鄰SNB點(diǎn)距離相對(duì)較遠(yuǎn)，因此牛拉法迭代時(shí)所需的平均迭代次數(shù)相對(duì)較多。

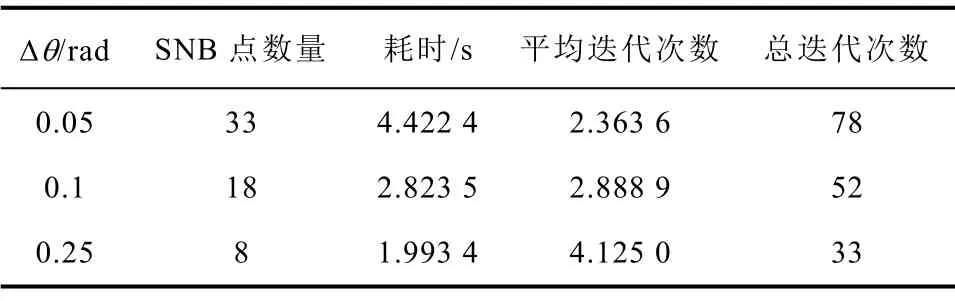
表4 不同Δθ 取值下的SVSRB計(jì)算效率對(duì)比Tab.4 Computational efficiency comparisons of SVSRB with different Δθ

隨著Δθ的不斷增大，構(gòu)建SVSRB所需SNB點(diǎn)數(shù)量不斷減少，計(jì)算時(shí)間也相對(duì)減少，但SVSRB的構(gòu)建精度與所搜索的SNB點(diǎn)數(shù)量密切相關(guān)，搜索的SNB點(diǎn)數(shù)量越多，構(gòu)建的SVSRB越準(zhǔn)確。因而，Δθ的增大在提高SVSRB構(gòu)建效率的同時(shí)，也降低了SVSRB構(gòu)建精度。圖6給出了在節(jié)點(diǎn)5、7形成的二維負(fù)荷有功注入空間內(nèi)，由不同Δθ下構(gòu)建的SVSR局部邊界。由圖6可知，Δθ取0.1rad時(shí)，SVSR區(qū)域由A、B和C三部分組成，Δθ取0.25rad時(shí)，SVSR區(qū)域由A組成。顯然，由區(qū)域A、B和C共同組成的區(qū)域更加接近真實(shí)的SVSR。Δθ取0.25rad時(shí)得到的SVSR區(qū)域較為保守，當(dāng)系統(tǒng)運(yùn)行在區(qū)域B或C時(shí)，會(huì)造成系統(tǒng)誤報(bào)警，因此，Δθ的取值需在SVSRB的搜索精度和搜索效率之間達(dá)到平衡。對(duì)比表4和圖6的計(jì)算結(jié)果可知：本文中Δθ取值為0.1rad是合理、可行的。

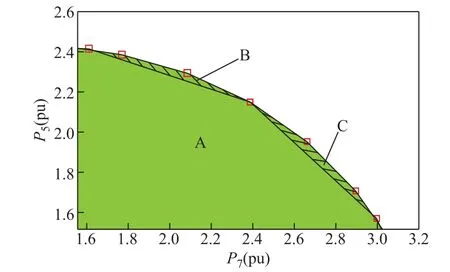
圖6 不同Δθ構(gòu)建的SVSRBFig.6 Constructed SVSRB compared with different Δθ

3.1.4 迭代步長(zhǎng)的分析

本節(jié)進(jìn)一步詳細(xì)分析了牛拉法收斂精度ε和BICGSTAB迭代法收斂閾值εb的選取過程。

1）牛拉法收斂精度ε的選取

采用邊界追蹤法搜索SVSRB時(shí)，SVSRB上相鄰SNB點(diǎn)處的系統(tǒng)運(yùn)行信息變化較小，若牛拉法收斂精度過小，則在提高SNB點(diǎn)計(jì)算精度的同時(shí)，也會(huì)增加牛頓迭代次數(shù)，使得SNB點(diǎn)的計(jì)算耗時(shí)明顯增加；而牛拉法收斂精度過大，則在減少牛頓迭代次數(shù)、提高SNB點(diǎn)計(jì)算效率的同時(shí)，可能無(wú)法保證SNB點(diǎn)的計(jì)算精度。

表5對(duì)比了牛拉法不同收斂精度對(duì)上述場(chǎng)景中SNB點(diǎn)8的計(jì)算精度和計(jì)算效率的影響。由表5可知，當(dāng)牛拉法收斂精度為10-2時(shí)，直接法即可獲得準(zhǔn)確的負(fù)荷裕度，且相較于其他收斂精度，具有較少的迭代次數(shù)和較高的計(jì)算速度。

表5 不同ε下SNB點(diǎn)8的計(jì)算效率對(duì)比Tab.5 Computational efficiency comparisons of 8th SNB with different ε

表6進(jìn)一步對(duì)比了牛拉法收斂精度ε分別為10-2和10-8時(shí)SNB點(diǎn)8處系統(tǒng)各節(jié)點(diǎn)的電壓幅值，并以收斂精度10-8為基準(zhǔn)，計(jì)算了各節(jié)點(diǎn)電壓幅值相對(duì)誤差。由表6可知，ε=10-2時(shí)的各節(jié)點(diǎn)電壓幅值相對(duì)誤差均低于0.05%，進(jìn)一步驗(yàn)證了所設(shè)牛拉法收斂精度的準(zhǔn)確性。

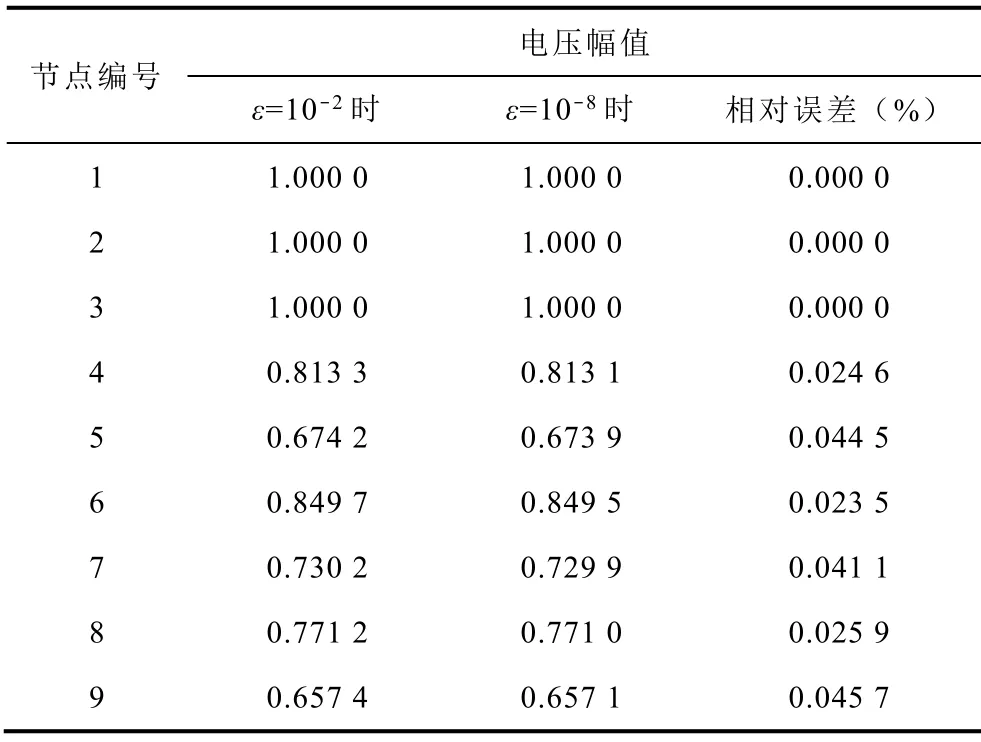
表6 不同ε下SNB點(diǎn)8處各節(jié)點(diǎn)電壓幅值對(duì)比Tab.6 Comparison of voltage magnitude of 8th SNB with different ε

綜上所述，本文設(shè)置的牛拉法收斂精度10-2可以很好地保證SNB點(diǎn)精度，且具有較高的計(jì)算效率，因此，本文中的牛拉法迭代步長(zhǎng)選為10-2。

2）BICGSTAB迭代法收斂閾值εb的選取

BICGSTAB迭代法是以當(dāng)前殘差與預(yù)設(shè)閾值進(jìn)行比較來判斷何時(shí)停止迭代，故對(duì)閾值的修改即可實(shí)現(xiàn)對(duì)求解精度的控制[24]。本文中，BICGSTAB迭代法主要用于求解牛頓迭代內(nèi)部的四個(gè)低維線性方程組式（4）～式（7），因此，其收斂閾值主要影響式（4）～式（7）的求解精度。然而，對(duì)式（4）～式（7）的求解并不是為了得到其精確解，而是為了使牛頓迭代可以向非線性方程組式（1）的真實(shí)解逼近，因此，BICGSTAB迭代法的收斂精度不需太高，能保證收斂即可。

通常，采用迭代求解法求解牛拉法內(nèi)部的線性方程組時(shí)，迭代求解法的收斂精度應(yīng)不低于牛拉法的收斂精度[31]，結(jié)合本文選取的牛拉法收斂精度，故BICGSTAB迭代法的收斂精度應(yīng)不低于10-2。而將BICGSTAB迭代法的求解精度調(diào)低可以有效降低內(nèi)部線性求解所需的迭代次數(shù)，提高計(jì)算效率，故本文中BICGSTAB迭代法的收斂閾值取為10-2。

3.1.5 三維SVSRB構(gòu)建

本節(jié)在二維SVSRB構(gòu)建的基礎(chǔ)上，進(jìn)一步借鑒文獻(xiàn)[23]的方法，以節(jié)點(diǎn)5、7、9的有功注入為坐標(biāo)軸，構(gòu)建了如圖7所示的三維SVSRB。由圖7的三維SVSRB搜索結(jié)果可知：本文所提基于CPUGPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法在二維、三維有功注入空間均可以實(shí)現(xiàn)SVSRB的準(zhǔn)確構(gòu)建。

圖7 WECC3機(jī)9節(jié)點(diǎn)系統(tǒng)的三維SVSRBFig.7 3-dimensional SVSRB of WECC 9 test system

進(jìn)一步，借鑒文獻(xiàn)[25]的安全域邊界近似方法，對(duì)圖7所示的三維SVSRB近似，結(jié)果如圖8所示，相應(yīng)的邊界近似解析表達(dá)式詳見附表1。

附表1 WECC-9節(jié)點(diǎn)系統(tǒng)的三維SVSRB近似邊界解析表達(dá)式系數(shù)App.Tab.1 Analytical expressions for the 3-dimensional SVSRB approximation hyperplanes of WECC-9 test system

圖8 WECC-9系統(tǒng)的三維SVSRB近似邊界Fig.8 Approximated 3-dimensional SVSRB of WECC-9 test system

3.2 Case13659pegase測(cè)試系統(tǒng)

WECC3機(jī)9節(jié)點(diǎn)系統(tǒng)算例驗(yàn)證了所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法的準(zhǔn)確性，本節(jié)進(jìn)一步以歐洲電網(wǎng)13 659節(jié)點(diǎn)系統(tǒng)為例[33]，采用所提的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法分別構(gòu)建case13659pegase系統(tǒng)的二維和三維SVSRB，以進(jìn)一步驗(yàn)證所提方法構(gòu)建大規(guī)模區(qū)域互聯(lián)電力系統(tǒng)SVSRB的可行性。

分別選擇節(jié)點(diǎn)4、5和節(jié)點(diǎn)4、6作為關(guān)鍵節(jié)點(diǎn)，采用本文所提的方法分別在節(jié)點(diǎn)4、5和4、6的二維有功注入空間構(gòu)建SVSRB，結(jié)果如圖9所示。進(jìn)一步，以節(jié)點(diǎn)4、5、6的有功注入量為坐標(biāo)軸構(gòu)建三維SVSRB，結(jié)果如圖10所示。

圖9 case13659pegase系統(tǒng)的二維SVSRBFig.9 2-dimensional SVSRB of European 13659PEGASE test system

圖9和圖10結(jié)果表明：本文所提基于CPUGPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法可以用于高維電力系統(tǒng)SVSRB的構(gòu)建，驗(yàn)證了本文所提方法的可行性。

進(jìn)一步，對(duì)圖9和圖10所得的二維、三維SVSRB進(jìn)行近似，結(jié)果如圖11和圖12所示。其中，圖9a和圖11a中，以節(jié)點(diǎn)4、5有功注入為坐標(biāo)軸的二維SVSRB近似解析表達(dá)式為

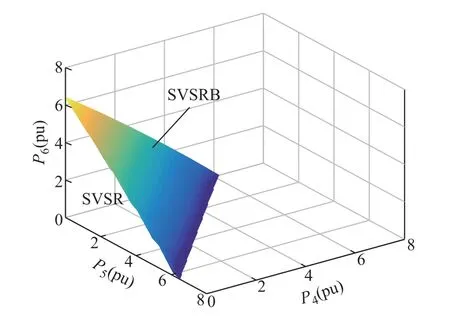
圖10 case13659pegase系統(tǒng)的三維SVSRBFig.10 3-dimensional SVSRB of European 13659PEGASE test system

圖11 case13659pegase系統(tǒng)的二維SVSRB近似邊界Fig.11 Approximated 2-dimensional SVSRB of European 13659PEGASE test system

圖12 case13659pegase系統(tǒng)的三維SVSRB近似邊界Fig.12 Approximated 3-dimensional SVSRB of European 13659PEGASE test system

圖9b和圖11b中，以節(jié)點(diǎn)4、6有功注入為坐標(biāo)軸的二維SVSRB近似解析表達(dá)式為

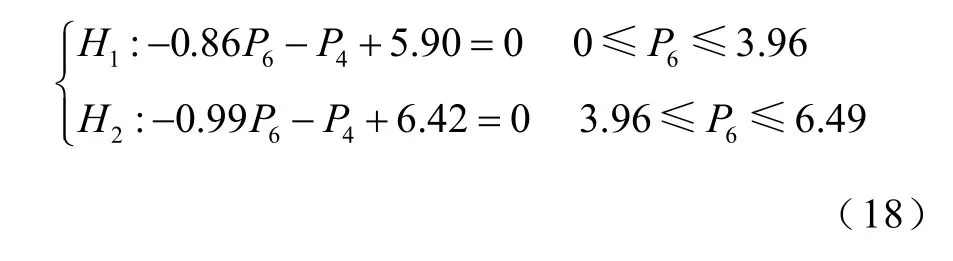
圖10和圖12中，以節(jié)點(diǎn)4、5和6有功注入為坐標(biāo)軸的SVSRB近似解析表達(dá)式詳見附表2。

附表2 歐洲電網(wǎng)13659節(jié)點(diǎn)系統(tǒng)三維SVSRB近似邊界解析表達(dá)式系數(shù)App.Tab.2 Analytical expressions for the 3-dimensional SVSRB approximation hyperplanes of European 13659PEGASE test system

3.3 SVSRB并行計(jì)算效率分析

為驗(yàn)證所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法構(gòu)建區(qū)域互聯(lián)電力系統(tǒng)SVSRB的有效性，本節(jié)分別以case2737sop、case3120sp、case7092、case9241pegase、case11624和case13659pegase測(cè)試系統(tǒng)為例，對(duì)基于CPUGPU異構(gòu)平臺(tái)的BICGSTAB迭代法與Jacobi+ILU(0)預(yù)處理相結(jié)合的計(jì)算方法、基于CPU平臺(tái)的BICGSTAB迭代法與Jacobi+ILU(0)預(yù)處理相結(jié)合的計(jì)算方法、基于CPU平臺(tái)的LU分解算法以及基于射線的直接法搜索二維、三維SVSRB的計(jì)算耗時(shí)進(jìn)行對(duì)比。上述四種算法搜索的二維和三維SVSRB計(jì)算耗時(shí)結(jié)果見表7和表8。

表7和表8中“—”表示測(cè)試系統(tǒng)的SVSRB構(gòu)建失敗。表中基于射線的直接法構(gòu)建電力系統(tǒng)SVSRB失敗的主要原因?yàn)椋豪秘?fù)荷參數(shù)二階導(dǎo)數(shù)預(yù)估SNB點(diǎn)初值存在給定初值不穩(wěn)定、不精確的現(xiàn)象，從而導(dǎo)致直接法計(jì)算部分測(cè)試系統(tǒng)SVSRB上的SNB點(diǎn)時(shí)結(jié)果不收斂。而基于CPU平臺(tái)的LU分解算法構(gòu)建電力系統(tǒng)SVSRB失敗的主要原因是由于LU分解算法受功率增長(zhǎng)方向的影響，不合理的功率增長(zhǎng)方向會(huì)使LU分解算法求解線性方程組式（4）～式（7）出現(xiàn)錯(cuò)誤解，從而導(dǎo)致牛頓迭代不收斂，SNB點(diǎn)求解失敗。對(duì)比表7和表8結(jié)果可知：基于射線的直接法雖理論上可行，但實(shí)際應(yīng)用時(shí)很難構(gòu)建出系統(tǒng)的SVSRB；基于CPU平臺(tái)的LU分解算法雖然可以快速搜索SVSRB，但該算法穩(wěn)定性較差；而對(duì)式（4）～式（7）采用Jacobi+ILU(0)兩階段預(yù)處理的BICGSTAB迭代法與牛頓迭代法相結(jié)合的方式使得本文所提基于邊界追蹤的直接法對(duì)于上述測(cè)試系統(tǒng)無(wú)論在CPU平臺(tái)還是CPU-GPU異構(gòu)平臺(tái)均可構(gòu)建出系統(tǒng)完整的SVSRB，有效驗(yàn)證了本文所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法適用性更強(qiáng)、魯棒性更高。其主要原因是：直接法對(duì)初值非常敏感，基于射線的直接法因以基態(tài)為起始點(diǎn)，基態(tài)與SNB點(diǎn)距離較遠(yuǎn)，直接法牛頓迭代時(shí)給定的初值不夠合理，因而牛頓迭代時(shí)SNB點(diǎn)收斂較慢甚至不收斂，不能構(gòu)建完整的SVSRB；而高度優(yōu)化的LU分解算法可快速求解式（4）～式（7）并結(jié)合邊界追蹤法可實(shí)現(xiàn)SVSRB的高效構(gòu)建，但基于CPU平臺(tái)的LU分解算法對(duì)功率增長(zhǎng)方向較為敏感，不當(dāng)?shù)墓β试鲩L(zhǎng)方向會(huì)導(dǎo)致SNB點(diǎn)求解失敗，無(wú)法構(gòu)建完整的SVSRB；而本文所提并行計(jì)算方法因給定的牛頓迭代初值非常接近相鄰待求解SNB點(diǎn)的真實(shí)值，SNB點(diǎn)初值精度較高，因此易獲得SNB點(diǎn)收斂解，便于構(gòu)建完整的SVSRB。

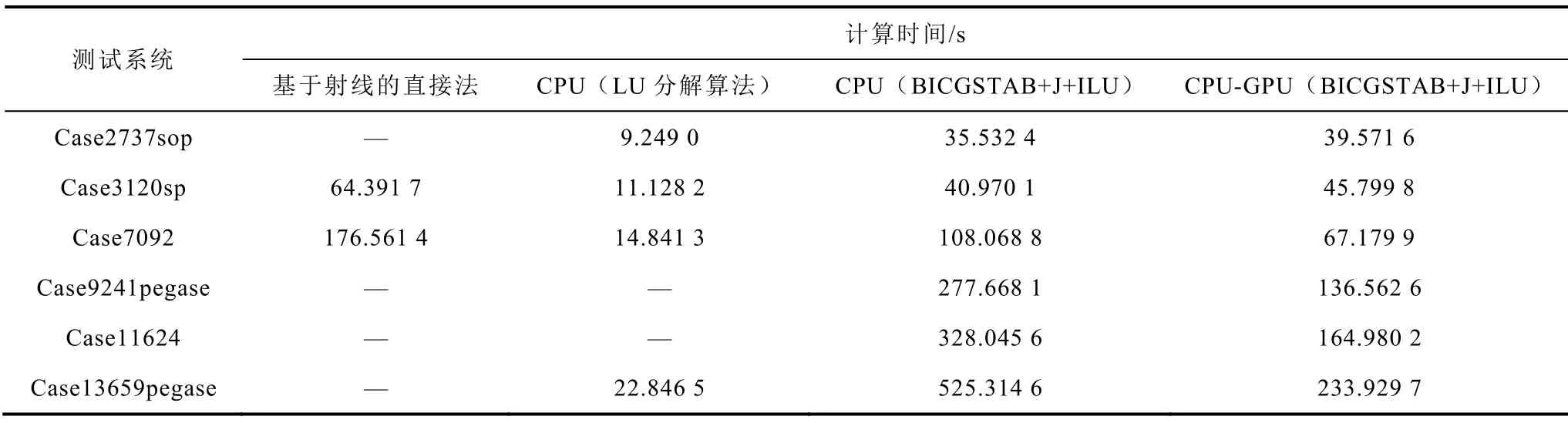
表7 不同測(cè)試系統(tǒng)的二維SVSRB計(jì)算時(shí)間對(duì)比Tab.7 Computational times of 2-dimensional SVSRB for different bulk power grids

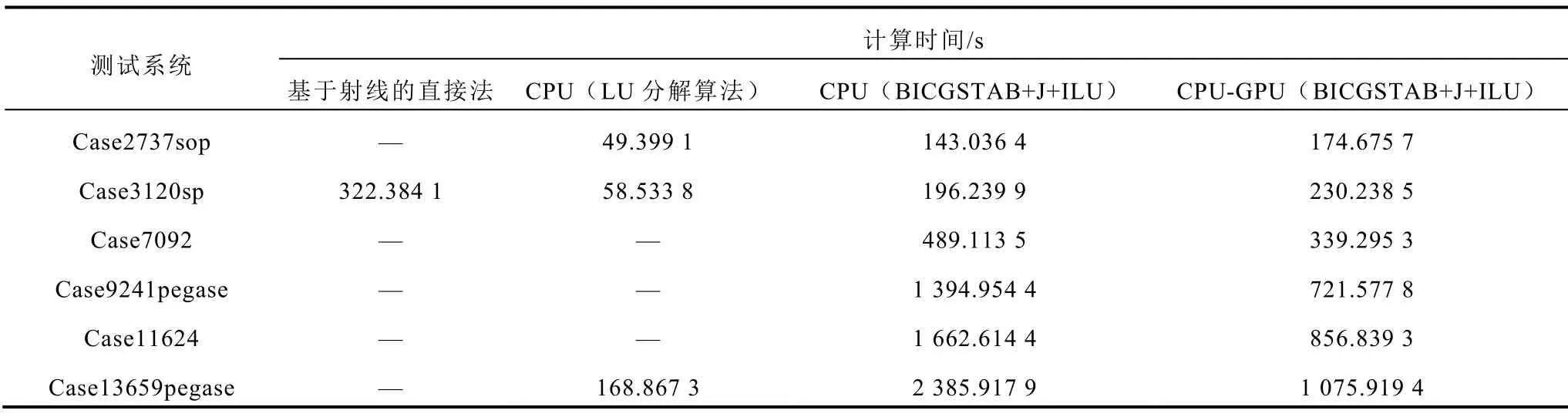
表8 不同測(cè)試系統(tǒng)的三維SVSRB計(jì)算時(shí)間對(duì)比Tab.8 Computational times of 3-dimensional SVSRB for different bulk power grids

進(jìn)一步分析表7和表8中CPU平臺(tái)和CPUGPU異構(gòu)平臺(tái)下采用基于邊界追蹤的直接法搜索SVSRB的結(jié)果表明：對(duì)于case2737sop和case3120sp測(cè)試系統(tǒng)，本文所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法構(gòu)建SVSRB的計(jì)算耗時(shí)相較基于CPU平臺(tái)的基于邊界追蹤的直接法更長(zhǎng)。其主要原因是：GPU作為CPU的外部設(shè)備，二者間的數(shù)據(jù)移植比較耗時(shí)[34]，利用GPU的并行技術(shù)加速對(duì)case2737sop和case3120sp測(cè)試系統(tǒng)線性方程組求解的同時(shí)，CPU和GPU之間的數(shù)據(jù)傳輸也會(huì)耗費(fèi)一定時(shí)間，且對(duì)于 case2737sop和case3120sp測(cè)試系統(tǒng)而言，CPU和GPU間的數(shù)據(jù)交互耗時(shí)要多于GPU并行求解帶來的加速性。當(dāng)測(cè)試系統(tǒng)規(guī)模大于case3120sp時(shí)，采用所提基于CPUGPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法構(gòu)建SVSRB的效率優(yōu)勢(shì)逐漸突顯，對(duì)case13659pegase測(cè)試系統(tǒng)的二維SVSRB，所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法構(gòu)建SVSRB的加速比是在CPU平臺(tái)中構(gòu)建SVSRB的2.25倍。

表9以CPU平臺(tái)構(gòu)建SVSRB的計(jì)算耗時(shí)為基準(zhǔn)，給出了采用所提基于CPU-GPU異構(gòu)平臺(tái)的SVSRB并行計(jì)算方法在搜索二維和三維SVSRB時(shí)的相對(duì)計(jì)算效率。由于采用CPU-GPU異構(gòu)平臺(tái)的SVSRB搜索方法在case2737sop和case3120sp系統(tǒng)的計(jì)算耗時(shí)大于在CPU平臺(tái)中的構(gòu)建耗時(shí)，因而對(duì)應(yīng)的表9中的計(jì)算效率提升量記為0。表9的計(jì)算耗時(shí)對(duì)比結(jié)果表明：對(duì)于大型區(qū)域互聯(lián)電力系統(tǒng)，采用本文所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法可進(jìn)一步加快SVSRB的構(gòu)建效率，降低了構(gòu)建SVSRB所需的計(jì)算耗時(shí)，驗(yàn)證了所提方法在構(gòu)建大規(guī)模區(qū)域互聯(lián)電力系統(tǒng)靜態(tài)電壓穩(wěn)定域中的有效性。

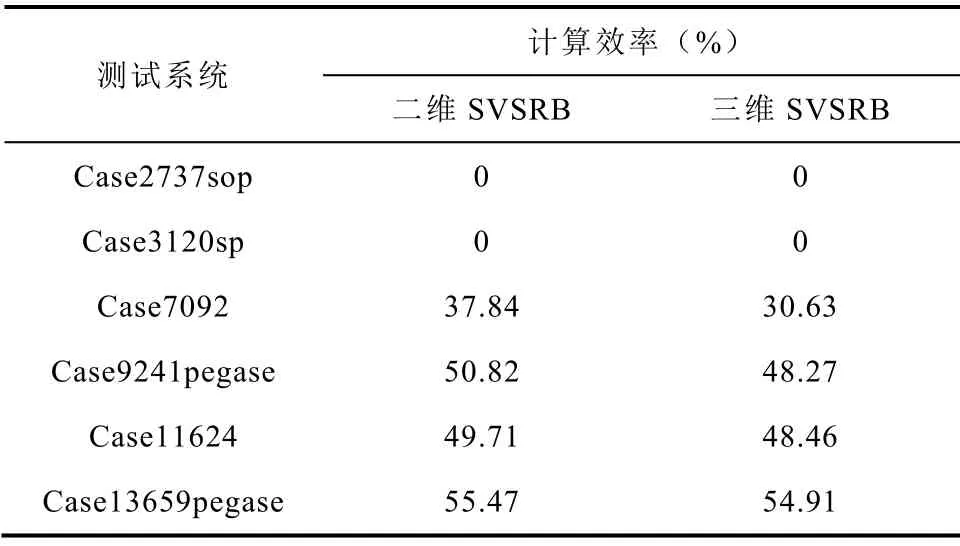
表9 不同測(cè)試系統(tǒng)的SVSRB并行計(jì)算效率對(duì)比Tab.9 Comparisons of computational efficiency for SVSRB in bulk power grids

上述對(duì)比結(jié)果表明：本文所提基于CPU-GPU異構(gòu)的靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法適用于區(qū)域互聯(lián)電力系統(tǒng)SVSRB的構(gòu)建，且在保證高精度的前提下具有較高的計(jì)算效率。

4 結(jié)論

本文提出一種基于CPU-GPU異構(gòu)的電力系統(tǒng)靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法，通過WECC3機(jī)9節(jié)點(diǎn)測(cè)試系統(tǒng)、波蘭電網(wǎng)2737節(jié)點(diǎn)測(cè)試系統(tǒng)和3120節(jié)點(diǎn)測(cè)試系統(tǒng)、歐洲電網(wǎng)7092節(jié)點(diǎn)測(cè)試系統(tǒng)、9241節(jié)點(diǎn)測(cè)試系統(tǒng)、11624節(jié)點(diǎn)測(cè)試系統(tǒng)和13659節(jié)點(diǎn)測(cè)試系統(tǒng)算例對(duì)本文所提方法的準(zhǔn)確性和有效性進(jìn)行了分析驗(yàn)證，相關(guān)結(jié)論如下：

1）所提方法將直接法與邊界追蹤法相結(jié)合，成功克服了直接法初值選擇的不足，且與CPU-GPU異構(gòu)平臺(tái)有效結(jié)合，解決了直接法計(jì)算量大、計(jì)算復(fù)雜度高的瓶頸。

2）所提方法可實(shí)現(xiàn)二維以及高維有功注入空間內(nèi)SVSRB的準(zhǔn)確構(gòu)建,且采用CPU-GPU異構(gòu)平臺(tái)有效降低了SVSRB的構(gòu)建耗時(shí)，提高了SVSRB的計(jì)算效率。

3）所提方法因給定初值穩(wěn)定，且采用Jacobi+ILU(0)兩階段預(yù)處理的BICGSTAB迭代法求解線性方程組，具有良好的算法穩(wěn)定性和適用性。

所提基于CPU-GPU異構(gòu)的電力系統(tǒng)靜態(tài)電壓穩(wěn)定域邊界并行計(jì)算方法雖可實(shí)現(xiàn)由SNB點(diǎn)構(gòu)成的SVSRB的快速構(gòu)建，但對(duì)于實(shí)際電力系統(tǒng)，LIB點(diǎn)同樣也可誘發(fā)系統(tǒng)電壓失穩(wěn)，因此，如何實(shí)現(xiàn)含SNB點(diǎn)和LIB點(diǎn)的SVSRB并行計(jì)算將是本文下一步的研究重點(diǎn)。

附 錄

（續(xù)）