多種數據結構實現迷宮問題詳解

章麗玲

(湖北第二師范學院 計算機學院，武漢 430205)

迷宮問題是“數據結構”課程中經典的非數值型的程序設計問題，理解迷宮問題的不同解決思路，對掌握《數據結構》課程的核心知識點具有非常重要的意義，本文將采用幾種典型的數據結構，利用不同的算法來實現迷宮問題。

1構造迷宮

用一個二維數組mg[M+2][N+2]表示迷宮，如圖1所示，M=8，N=8，狀態為0時表示對應方塊是通道(可走)，狀態為1時表示對應方塊是障礙物(不可走)，為了算法方便，一般迷宮的外圍加一條圍墻。設定入口為mg[1][1]，出口為mg[8][8]。

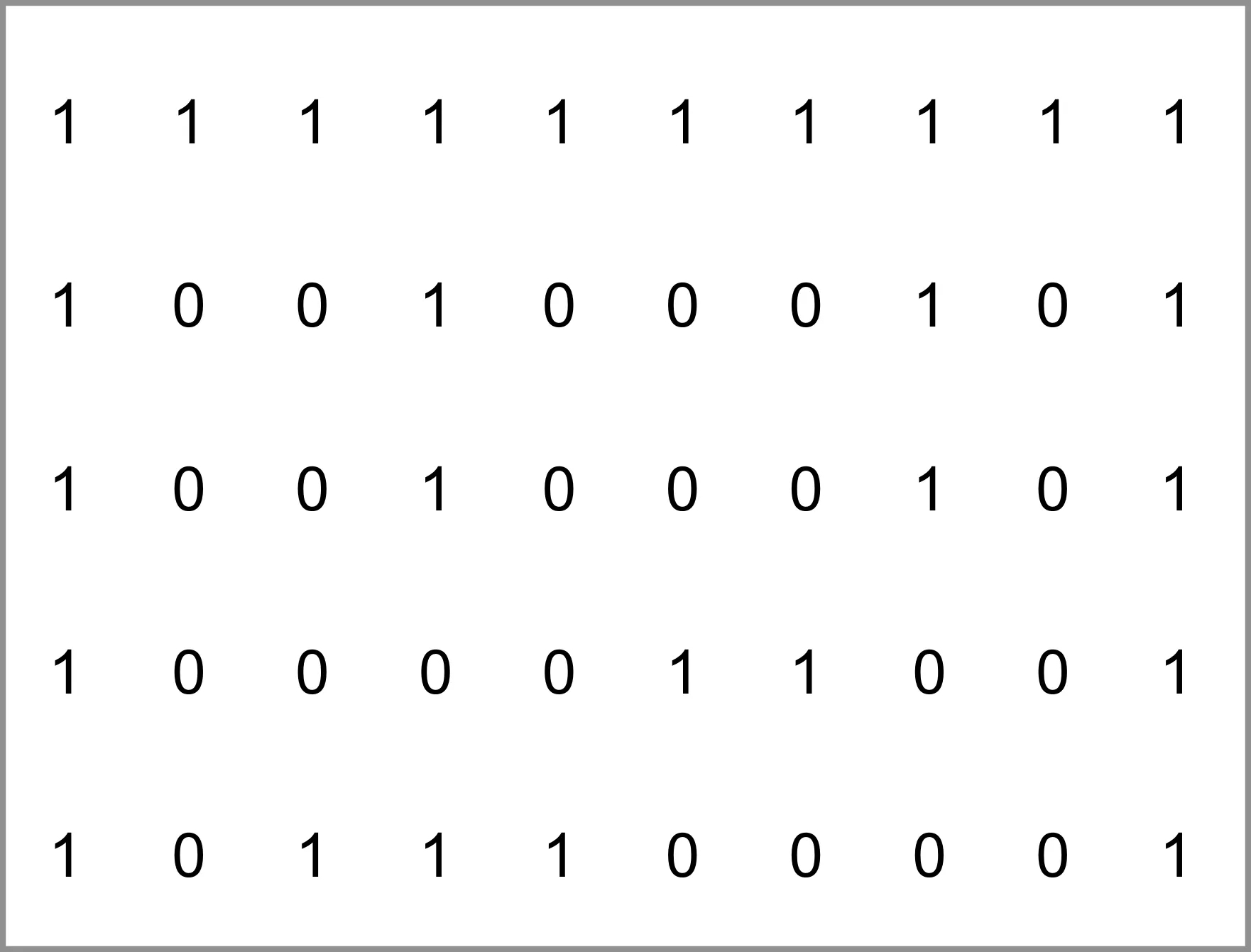
圖1 迷宮圖

2 算法思路

求解迷宮問題通常采用“窮舉探索求解法”，即從入口出發，順某一方向向前探索，若能走通，則繼續往前走，否則沿原路退回(回溯)，換一個可行的方向再繼續探索，直至所有可能的通路都探索到為止。為了保證在任何位置上都能原路退回，常用的數據結構有棧和隊列，如果把迷宮中的每一個位置看作是一個點的話，那么就可以把迷宮轉換為一個個相連或分斷的各個頂點之間的關系，因此，可以使用另一種數據結構——無向圖來表示。下面將針對不同的數據結構來實現迷宮問題。

2.1 用棧實現迷宮

棧是一種只能在一端進行插入和刪除操作的線性表。允許進行插入和刪除操作的一端稱為棧頂(top)，另一端稱為棧底(bottom)。棧的主要特點是后進先出，正是棧的這一特點使得它成為解決迷宮問題的數據結構。

2.1.1 數據結構設計

采用順序棧實現迷宮，迷宮棧聲明如下：

typedef struct

{

int i; //當前方塊的行號

int j; //當前方塊的列號

int di; //di是下一相鄰可走方位的方位號

}Box;

typedef struct

{

Box data[MaxSize]; //棧中每一個結點存放i,j,di.

int top;

} StType;

2.1.2 棧實現的算法設計思路

對于迷宮中的每個方塊，有上、下、左、右四個方塊相鄰，如圖2所示，第i行第j列的當前方塊的位置記為(i,j)，規定上方方塊為方位0，并按順時針方向遞增編號。在試探過程中，按從方位0到方位3的方向查找下一個可走的相鄰方塊。為了保證在任何位置上都能沿原路退回(稱為回溯)，需要保存從入口到當前位置的路徑上走過的方塊，若一個非出口方塊(i,j)是可走的，將它進棧，每個剛剛進棧的方塊，其方位di置為-1(表示尚未試探它的周圍)，然后開始從方位0到方位3試探這個棧頂方塊的四周，如果找到某個方位d的相鄰方塊(i1,j1)是可走的，則將棧頂方塊(i,j)的方位di置為d，同時將方塊(i1,j1)進棧，再繼續從方塊(i1,j1)做相同的操作。若方塊(i,j)的四周沒有一個方位是可走的，將它退棧，繼續其他的路徑。實際上，該算法思路是利用棧的后進先出的特點，一步一步地查找可走的方塊，直到找到出口為止，該方法類似于圖的深度優先搜索方法。

圖2 迷宮方位圖

2.1.3 算法描述

Bool mgpath(int xi,int yi,int xe,int ye) //求解路徑為(xi,yi)->(xe,ye)

{

將入口(xi,yi)進棧(其初始方位設置為-1);

mg[xi][yi]=-1;

while(棧不空)

{

取棧頂方塊(i,j,di);

if((i,j)是出口(xe,ye))

{輸出棧中全部方塊構成一條迷宮路徑；

return true;}

查找(i,j,di)的下一個相鄰可走方塊；

If(找到一個相鄰可走方塊)

{該方塊為(i1,j1)，對應的方位為d；

將棧頂方塊的di設置為d;

(i1,j1,-1)進棧；

mg[i1][j1]=-1;}

if(沒有找到(i,j,di)的任何相鄰可走方塊)

{將(i,j,di)出棧；

mg[i][j]=0; }

}

return false;

}

2.2 用隊列實現迷宮

隊列也是一種操作受限的線性表，其限制為僅允許在表的一端進行插入操作，而在表的另一端進行刪除操作。進行插入的一端稱為隊尾(rear)，進行刪除的一端稱為隊首(front)。隊列的主要特點為“先進先出”，可以利用隊列的這個特點來實現迷宮問題。

2.2.1 數據結構設計

采用順序隊列qu保存走過的方塊，這里不使用循環隊列，因為在找到出口時需要利用隊列中的所有方塊查找一條迷宮路徑，因此要求順序隊列qu有足夠大的空間。

typedef struct

{ int i,j; //方塊的位置

int pre; //本路徑中上一方塊在隊列中的下標

} Box; //方塊類型

typedef struct

{

Box data[MaxSize];

int front,rear; //隊頭指針和隊尾指針

} QuType; //順序隊類型

2.2.2 隊列實現算法設計思路

首先將入口(xi,yi)進隊，在隊列qu不為空時循環，出隊一個方塊e，其下標為front，然后查找方塊e的所有相鄰可走方塊，假設e1和e2兩個方塊，將它們進隊，它們在隊列中的位置分別是rear1和rear2，并且將他們的pre均設置為front，當找到出口時，通過出口方塊的pre值前推找到入口，所有經過的中間方塊構成一條迷宮路徑。實際上，該算法思路是利用隊列的特點，一層一層向外擴展查找可走的方塊，直到找到出口為止，該方法類似于圖的廣度優先搜索方法。

2.2.3 算法描述

Bool mgpath1(int xi,int yi,int xe,int ye)

{

將入口(xi,yi)的pre置為-1并進隊；

mg[xi][yi]=-1;

while(隊列qu不空)

{出隊一個方塊e，其在隊列中的位置是front;

if(方塊e是出口)

{ 輸出一條路徑; return true;}

for(對于方塊e的所有相鄰可走方塊e1)

{ 設置e1的pre為front;

將方塊e1進隊；

將方塊e1的迷宮數組值設置為-1;}

}

return false;

}

2.3 用圖搜索方法實現迷宮

圖都是由頂點和邊構成的，可以把迷宮圖中的每一個方塊看成一個頂點，方塊和方塊之間的連通性看出頂點與頂點的邊，因此，可以把迷宮問題看成圖的問題，可采用圖的深度優先搜索和廣度優先搜索算法來求解迷宮問題。

2.3.1 圖的數據結構設計

常用的圖的存儲結構有鄰接矩陣和鄰接表。這里采用鄰接表比較好，因此首先需要將迷宮圖的二維矩陣轉化為對應的鄰接表，其思路為：一個方塊看成一個頂點，編號為(i,j)，根據周圍4個方向狀態為0的方塊建立鄰接表，鄰接表的頭結點是一個二維數組。對應的鄰接表類型聲明如下：

typedef struct Anode

{ int i,j;

Struct Anode *nextarc;

} ArcNode; //邊節點類型

typedef struct Vnode

{ ArcNode *firstarc; //指向第一個相鄰可走方塊

} VNode; //頭結點

typedef struct

{ VNode adjlist[M+2][N+2];

} AdjGrapgh;

Typedef struct

{ int i;

Int j;

} Box; //定義方塊

Typedef struct

{ Box data[MaxSize];

Int length;

} PathType; //定義路徑類型

鄰接表的表頭用一個二維數組adjlist表示,adjlist[i][j]僅含有一個firstarc指針，它指向方塊(i,j)的四周可走方塊構成的一個單鏈表，圖一對應的迷宮鄰接表如圖3所示。

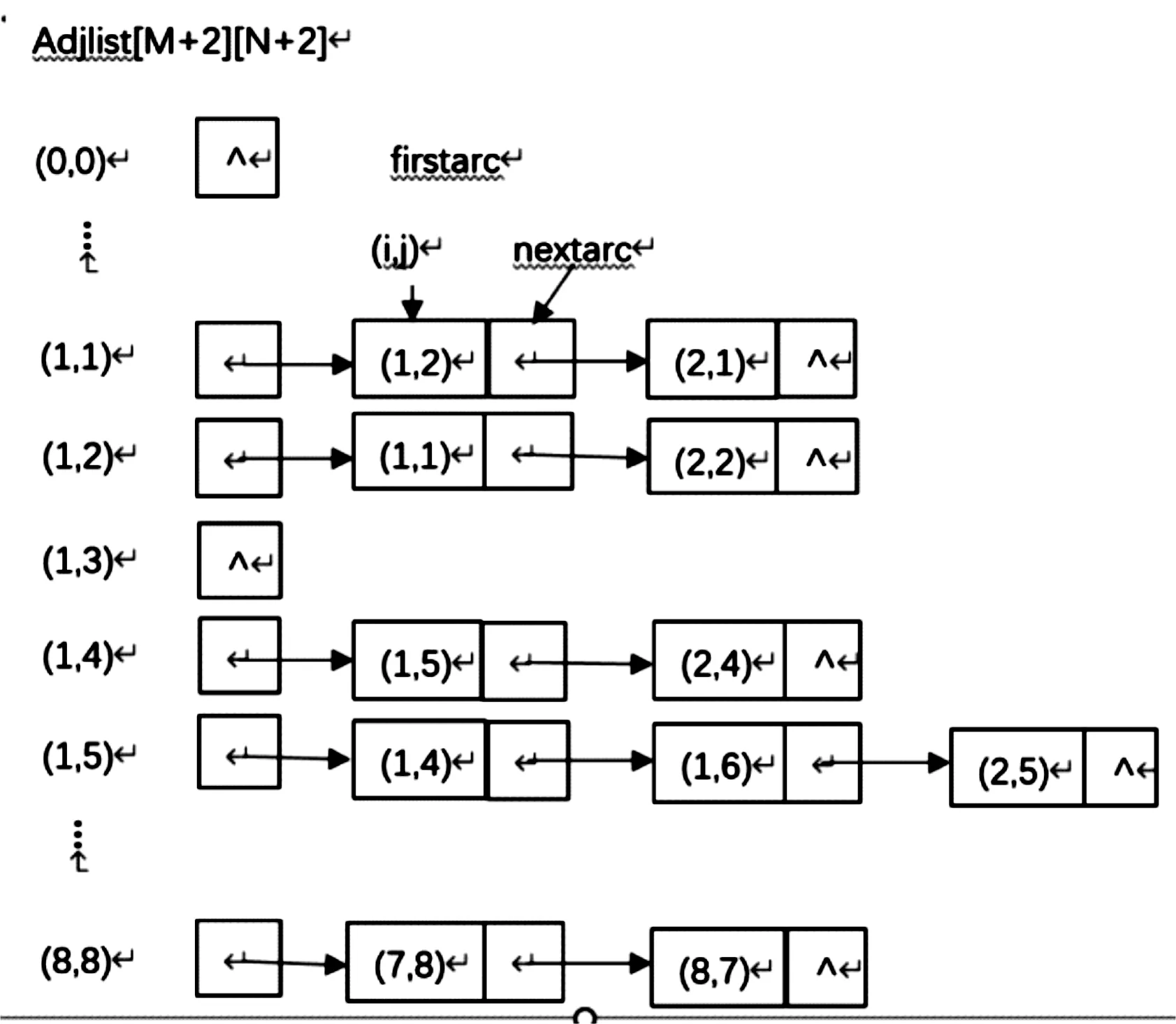
圖3 迷宮鄰接表

2.3.2 算法設計

在搜索迷宮路徑時可以采用DFS(深度優先搜索)或者BFS(廣度優先搜索)算法，將訪問標記數組改為visited[M+2][N+2]，入口作為初始頂點，結束條件為找到出口。下面算法采用的深度優先搜索算法求(xi,yi)到(xe,ye)的所有路徑。

Void FindPath(AdjGraph *G,int xi,int yi,int xe,int ye,PathType path)

{ ArcNode *p;

visited[xi][yi]=1; //入口置已訪問標記

入口加入路徑，并將路徑長度加一

If(xi==xe && yi==ye) //找到出口

{ 輸出迷宮路徑； }

p=G->adjlist[xi][yi].firstarc;//p指向頂點v的第一條邊頂點

//采用遞歸的方法深度優先搜索

while(p!=null)

{ if(visited[p->i][p->j]==0)

FindPath(G,p->i,p->j,xe,ye,path);

P=p->nextarc;

}

visited[xi][yi]=0;

}

3 小結

線性表、棧、隊列、遞歸、圖、深度優先搜索(DFS)和廣度優先搜索(BFS)屬于“數據結構”課程的核心知識點，他們既是教學重點，又屬于教學難點，然而，通過求解迷宮問題，可以把這些知識點串在一起，使學生能夠靈活地應用線性表解決實際問題，分清棧和隊列應用的區別，為了拓展學生的邏輯思維，將迷宮問題描述成圖的搜索問題，可采用深度優先搜索的遞歸思想和廣度優先搜索的非遞歸思想來實現。總之，采用多種數據結構來實現迷宮問題可大大提高學生對數據結構核心知識點的理解深度，提高學生對迷宮算法的多維性理解能力。