無刷直流電機模糊PID控制及建模仿真*

郭文韜，單樹清，劉二林，馬殷元，金寶寶，鐘佩甫，張 正

（蘭州交通大學創新創業學院，蘭州730070）

0 引言

隨著永磁材料和電子技術的不斷發展，無刷直流電機（Brushless DC Motor，BLDCM）進入了快速發展階段。與有刷直流電機相比，無刷直流電機利用功率管電路的電子換相代替有刷直流電機的機械換相，消除了有刷直流電機發生故障的主要根源[1]。無刷直流電機結構緊湊、效率高、可靠性強，并且兼有有刷直流電機的良好機械特性和調節特性，廣泛應用于工業精確控制、精密伺服系統、醫療設備等領域[2]。無刷直流電機有著廣闊的應用前景，對其精準控制等方面深入研究有很大的必要性。

目前，BLDCM控制系統國內外研究熱點主要有3個方向：（1）轉矩脈沖轉動抑制；（2）位置檢測技術；（3）智能控制算法對于無刷直流電機的控制優化[3]。謝志誠等[4]在MATLAB軟件中建立無刷直流電機控制系統仿真模型，編寫單神經元PID速度調節器的S-Function函數，實現電機仿真，取得良好的控制效果。馬曉爽等[5]采用速度PI控制和電流PI控制雙閉環控制系統，在MATLAB/Simulink平臺搭建仿真模型，在不同負載下，控制系統表現出有著良好的動態和靜態性能。本文分析了無刷直流電機的數學模型和工作原理，在MATLAB/Simulink環境中搭建出無刷直流電機控制系統仿真模型，采用雙閉環模糊PID控制算法對控制系統進行速度調節，得到電機的轉速和轉矩等參數波形圖，并與傳統PID控制算法相比較，仿真結果驗證了雙閉環模糊PID控制算法對電機控制具有良好的控制效果。

1 無刷直流電機原理

無刷直流電機由電機本體、位置傳感器、控制系統三部分組成。其基本原理是根據位置傳感器從電機轉子檢測轉子位置信息，控制驅動電路根據轉子位置信號，輸出PWM波驅動逆變橋依次按順序導通，產生旋轉磁場驅動永磁轉子轉動[6]，控制原理如圖1所示。

圖1 無刷直流電機控制原理

電機本體結構類似于倒裝式的直流電機，恰與有刷直流電機安裝結構相反，轉子側安裝永磁體，定子側安裝有三相電樞繞組，分為A、B、C三相，每相間隔120°電位差，采用星型連接。

位置傳感器采用霍爾傳感器，利用霍爾效應檢測轉子磁極的相對位置，計算為驅動控制電路提供轉子位置信息，并計算轉子實際轉速。驅動控制電路根據轉子位置信號通過驅動三相全橋逆變橋按順序導通，實現電機的電子換相功能。換相采用兩兩導通方式，每次有兩個功率開關導通，每隔60°逆變橋便會改變一次導通狀態，每個開關連續導通120°[7]。

2 無刷直流電機數學模型

控制系統中的全橋逆變驅動方式為兩兩導通星型連接，采用電機的相變量建立無刷直流電機的數學模型和時域狀態方程，計算結果也較為準確。為了分析過程便于分析，需要在電機理想狀態下運行，本文對電機做出以下幾點假設[8]：（1）電機三相繞組完全對稱且各繞組電阻、電感、互感等各參數均一致；（2）驅動電路中功率開關的通斷反應條件均處于理想狀態；（3）齒槽效應忽略不計；（4）定子繞組的反電動勢假定為平頂寬度為120°的梯形波；（5）磁芯飽和、渦流損耗和磁滯損耗等忽略不計。

2.1 電壓方程

基于上述假設以及無刷直流電機特性，根據無刷直流電機的等效電路（圖2），可得到無刷直流電機電壓方程：

圖2 無刷直流電機等效電路

式中：uA、uB、uC分別對應的是電機定子三相繞組端電壓，V；iA、iB、iC分別對應的是電機三相繞組相電流，A；RA、RB、RC分別為三相繞組的相電阻，Ω；LA、LB、LC為三相繞組的電感，H；LAB為三相繞組中的A相繞組和B相繞組之前的互感，H；即LAC、LBA、LBC、LCA、LCB均為兩相繞組之間的互感，H；eA、eB、eC分別為電機三相繞組反電動勢，V；un為繞組的中心點電壓，V。

本文電機電樞繞組采用星型連接，相電流之間關系為：

無刷直流電機在上述假設的理想狀態下，由于電樞繞組為三相完全對稱結構，各繞組的互感和電阻相同，進而三相電樞繞組的兩兩繞組之間的互感也是相同的，因此，得出以下關系：

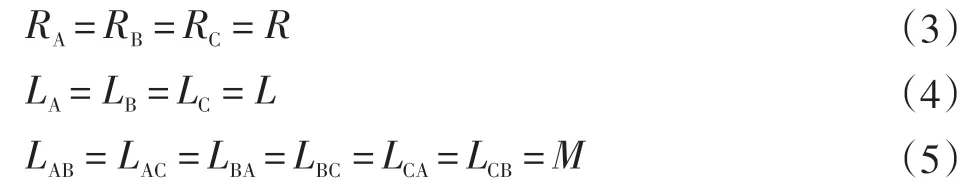
進一步化簡，最后得到電機電壓方程：

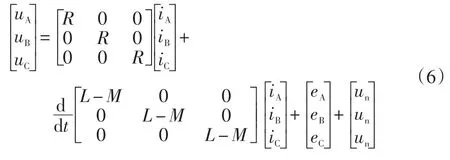
2.2 電磁轉矩方程

電機運行時，從電源吸收的電功率主要銅耗、鐵耗及電磁功率3部分組成。其中銅耗和鐵耗占總功率中的極小部分，轉子力矩占主要部分，這部分功率就是電磁功率。忽略鐵耗和銅耗后，電磁功率是定子三相繞組的相反電動勢與相電流的乘積之和：

在電機空載工況下，忽略轉子的機械損耗和其他損耗，則電機的電磁功率將全部轉化為轉子動能：

式中：Pe為電磁功率，W；Te為電磁轉矩，N?m2；ω為電機機械角速度，rad/s。

2.3 電機運動方程

在電機工作時，根據電機轉子本身特性及負載狀況，可得出電機運動方程：

式中：TL為負載轉矩，N?m；J為電機轉子轉動慣量，N?m；BV為粘滯摩擦因數。

式（7）、（10）、（11）共同組成了電機的數學模型公式。

3 無刷直流電機控制系統仿模型

基于無刷直流電機的主要工作原理及數學模型，利用MATLAB/Simulink工具進行電機控制系統進行仿真。無刷直流電機控制系統具有非線性、強耦合性等特征，傳統PID控制算法無法精準地實現無刷直流電機轉速控制，本文采用模糊PID雙閉環控制算法對無刷直流電機控制系統進行分析，并在Simulink中搭建出無刷直流電機的雙閉環模糊PID控制系統仿真模型。

3.1 電機總體模塊

電機總體模塊是無刷直流電機控制系統的控制對象，由3部分組成：電壓模塊、轉矩模塊和電機運動方程模塊。主要依據無刷直流電機的數學模型和基本工作原理搭建而來，如圖3所示。

圖3 電機總體模塊

3.1.1 電壓模塊

目前求取電機反電動勢主要有3種方法：傅里葉變換法、有限元法及分段線性法。與另外兩種方法相比，分段線性法結構簡單、精準度較高、計算量小。在MAT?LAB中利用S-function函數，根據轉子的相對位置，將轉子一個運行周期分成6個階段，根據某時刻轉子的相鄰兩個狀態夾角位置和轉速信號，確定各相反電動勢的狀態。

位置傳感器檢測的轉角信號不能直接使用，需要將轉子信號轉換為電機的位置信號，通過Simulink中的S-Function函數計算可得。各相反電動勢狀態如表1所示。

表1 轉子位置和反電動勢關系

根據轉子實時位置，電機反電動勢不斷變化，電壓模塊是根據電機三相端電壓和電機反電動勢輸出電機的三相電流，仿真模型如圖4所示。

圖4 電機本體仿真模型

3.1.2 轉矩模塊

根據無刷直流電機的轉矩方程式可得出電機轉矩模塊。其輸入為電機本體模塊中的輸出電流、反電動勢以及角速度，輸出為電機轉矩，仿真模型如圖5所示。

圖5 轉矩模塊

3.1.3 轉速模塊

電機轉速模塊是根據無刷直流電機的運動學方程式而得，由輸入的電磁轉矩和負載轉矩經過數值算法，輸出得到電機角速度w。通過轉速計算公式即可得到電機的轉速模塊[8]如圖6所示。

圖6 轉速模塊

3.2 電壓逆變模塊

逆變模塊主要作用為將功率變換將輸入的直流電壓根據PWM波脈沖信號控制下轉變為可調節的電壓和頻率。在Simulink提供通用逆變器，其中包含有MOSFET等功率開關，可設置為三相全橋MOSFET功率開關模式，簡化了使用6個全橋逆變電路。逆變模塊的輸入直流電源和PWM波信號，通過三相全橋功率開關得到三相電壓uA、uB、uC。電壓逆變模塊如圖7所示。

圖7 電壓逆變模塊

3.3 轉速模糊控制模塊

本文轉速控制模塊采用模糊PID控制算法，模糊PID算法根據設定轉速和實際轉速之間的誤差及誤差變化率，記過模糊控制算法的模糊推理對PID參數值進行實時自整定，調節PID參數，達到良好的控制效果[9]。

利用MATLAB中的Fuzzy Logic Toolbox，輸入為誤差E和誤差率EC，輸出變量ΔKp、ΔKi、ΔKd，通過修正參數ΔKp、ΔKi、ΔKd，對PID控制器中的參數值進行不斷修正，提高PID控制的時變性、魯棒性和抗干擾能力。輸入E、EC和輸出ΔKp、ΔKi、ΔKd的基本論域均選取為[-3 3]變化范圍，共分{-3，-2，-1，0，1，2，3}7個等級。各變量的基本論域相對應的模糊子集為{NB，NM，NS，Z，PS，PM，PB}，即{負大，負中，負小，零，正小，正中，正大}。輸入變量E和EC采用的高斯型隸屬度函數，輸出變量ΔKp、ΔKi、ΔKd均采用三角形隸屬度函數。通過專家經驗和長期試驗結果，設定模糊控制規則，如表2～4所示。

表2 ΔKp模糊規則表

表3 ΔKi模糊規則表

設定控制規則后，輸出值ΔKp、ΔKi、ΔKd論域范圍內隨輸入E、EC變化的變化而不斷發生變化，其變化如圖8~10所示。

圖8 ΔKp變化

經過模糊控制器的模糊計算，得到3個整定參數ΔKp、ΔKi、ΔKd，對PID控制器進行在線調整，最終得到的輸出量為三相電流的參考電流的幅值。轉速模糊控制仿真模塊如圖11所示。

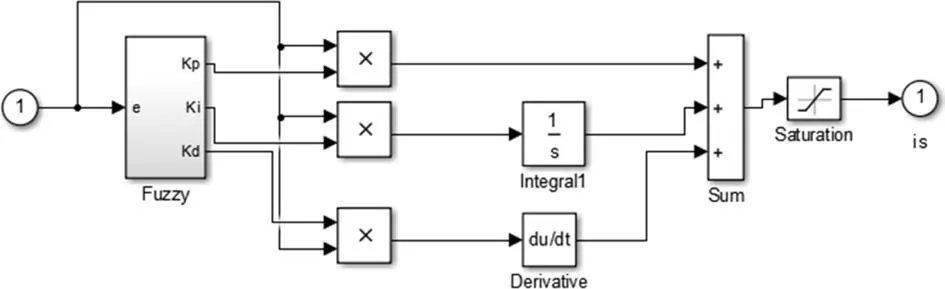
圖11 轉速模糊控制仿真模塊

表4 ΔKd模糊規則表

3.4 參考電流模塊

三相參考電流，采用分段線性法，在Simulink中利用S-Function函數，根據轉子位置信號不斷變化，求得三相參考電流在不同電機轉子位置時的三相參考電流不同狀態，如表5所示。

表5 參考電流與轉子位置信號關系表

3.5 電流控制模塊

滯環控制器是控制系統的電流控制模塊的核心內容，其主要作用是對電機電流進行調節。滯環模塊輸入為三相參考電流及三相實際電流，通過參考電流與實際電流之間的電流差Δi與滯環控制器中設定的滯寬h相比較，根據Δi和h之間的大小關系，判斷功率管的導通與關斷。同時調節實際電流上升和下降，保證實際電流在設定允許范圍之內。由控制功率開關輸出PWM波信號，作為電壓逆變器的輸入脈沖信號。電流滯環控制模塊如圖12所示。

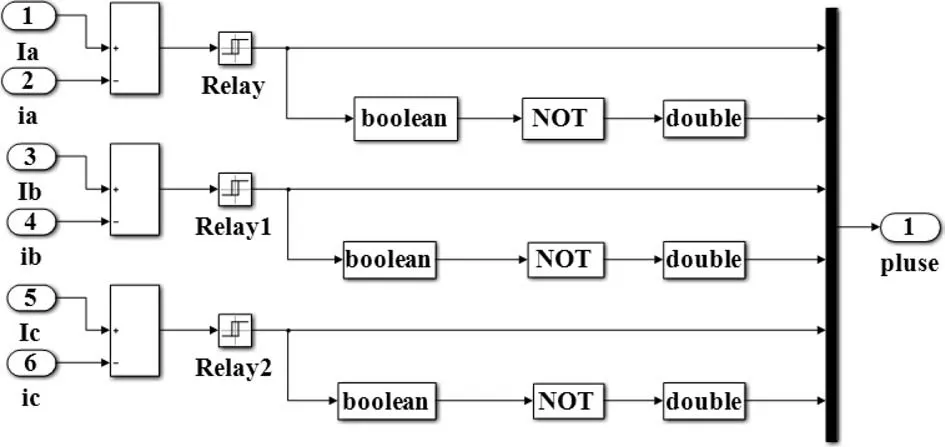
圖12 電流滯環模塊

3.6 控制系統仿真模型

無刷直流電機控制系統主要包含上述的電機總體模塊、電流滯環模塊、電壓逆變模塊、參考電流模塊、轉速控制模塊等部分，按照邏輯順序將上述子模塊進行有序組合，搭建成完整的無刷直流電機控制仿真模型，如圖13所示。

圖13 無刷直流電機控制系統仿真模型

3.7 仿真結果

控制系統仿真模型以空載啟動方式，電機繞組為R=3.4 Ω，定子電感L=0.002 H，互感M=-0.006 H，輸入電壓DC24 V，轉動慣量J=0.000 32，參考轉速n=1 000 r/min，驗證電機的靜態和動態調節性能。從相電壓、轉矩等仿真波形，可以看出電機控制系統的仿真性能，從仿真圖中可以看出，電機三相電壓較為平穩，電機轉矩在啟動后趨于穩定。如圖14～15所示。

圖9 ΔKi變化

圖10 ΔKd變化

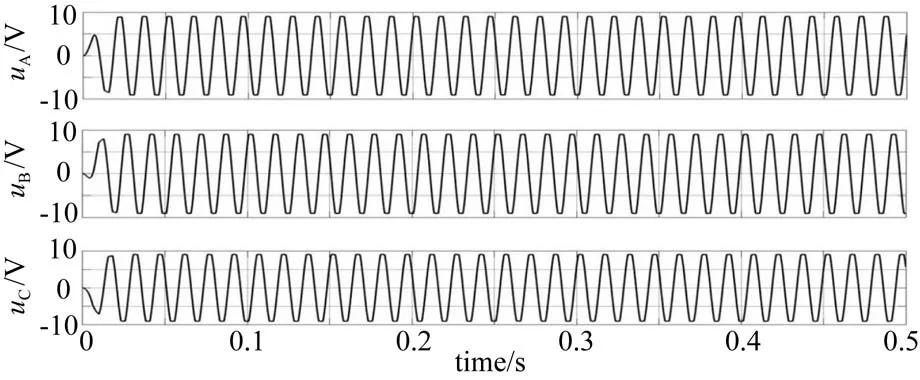
圖14 電壓uA、uB、uC波形

圖15 轉矩Te波形

在相同條件下，搭建出普通PID控制系統，與模糊PID控制仿真模型相比較，兩者轉速波形如圖16所示。

圖16 兩種轉速n波形

從圖16中可以看出模糊PID控制系統和傳統PID控制系統相比，超調量小，響應速度快，電機能夠快速達到設定轉速值，并保持穩定，仿真結果表明，模糊PID控制具有更好的調速控制效果。

4 結束語

本文對無刷直流電機控制系統進行數學模型推導以及控制系統仿真模型搭建，通過采用速度環和電流環雙閉環控制，采用模糊PID控制算法對控制系統進行仿真驗證，與理論分析基本相吻合，模糊控制對PID參數進行整定，能夠對無刷直流電機實現良好的動態響應和動態調節。該模型在Simulink中采用模塊化和S-Function函數設計，采用模糊控制算法實現控制策略，為無刷直流電機控制的分析等方面提供參考學習。