調制邊頻帶不對稱性及對齒輪故障診斷影響的研究

張 偉，柯 昭，曾嘉銘

（湖北西塞山發電有限公司，湖北黃石435000）

0 引言

齒輪傳動在現代機械傳動中廣泛運用，主要通過齒輪組嚙合來實現機械變速或轉向等傳動作用，其嚙合狀態將直接影響傳動效果[1]，理論講嚙合傳動過程中由于承載負荷的變化、轉速的變化，加工精度和齒輪故障等原因不可避免會造成振動和沖擊。從而形成調制效應，問題齒輪的轉頻或其倍頻（故障信號）成為“調制信號”，齒輪嚙合頻率即“載頻信號”，只有對這些信號進行時域和頻域分析后，才能獲得準確診斷結果[2]。一般齒輪箱內有多個不同轉數的軸和齒輪配合使用，因此，含有不同頻率分量，而不同故障類型又具有不同的頻率特征。評定齒輪嚙合狀態的關鍵頻率之一是齒輪的嚙合頻率（齒輪的齒數×轉速），然而，應該指出，嚙合頻率不像軸承故障頻率那樣重要，所有嚙合的齒輪都產生一定幅值的嚙合頻率，所有嚙合頻率都有一定幅值的齒輪轉速的邊帶。如果齒輪狀態良好，并且彼此良好配合（沒有明顯的不對中、齒輪游移或齒輪偏心、斷齒），則嚙合頻率及其諧波頻率和那些邊帶頻率的幅值應該很小，尤其是那些邊帶。嚙合頻率的幅值調制及其諧頻，雖然能夠揭示出齒輪嚙合中的一些有用的信息，如齒輪不對中、負荷大小、偏心等；但是嚙合頻率通常不能揭示斷齒、裂紋或碎齒，這類齒輪故障及缺陷與邊帶頻率密切相關，由這類故障與缺陷而引起振動能量增加，大都反映在邊頻分量上。因此，對齒輪傳動系統進行邊帶分析和識別，可完善齒輪傳動系統狀態監測和故障診斷的手段，發現早期的齒輪故障及缺陷，從而避免設備產生不可修復的損壞。但因調制方式的不同，特別是受到不同頻率分量調制后故障特征信號變得更加復雜，嚙合頻率幅值信號不再具有特征性，在嚙合頻率兩邊所產生的邊頻帶也不再以嚙合頻率為中心形成對稱分布特征，從而造成利用故障特征頻譜分析法進行齒輪傳動系統狀態監測和故障診斷的巨大難度[3]。

1 嚙合頻率及邊頻帶產生機理

1.1 嚙合頻率

圖1 所示為一對簡單嚙合齒輪副。從齒輪嚙合頻率開始，用數學公式說明嚙合頻率產生的機理。

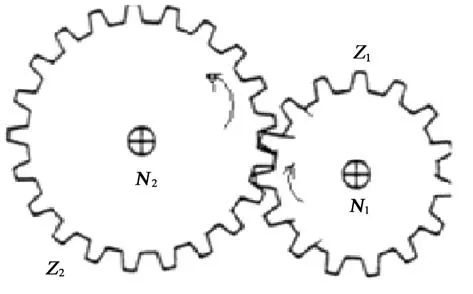
圖1 簡單齒輪副

轉頻：

式中：n1、n2分別為大、小齒輪轉速，r/min；f1、f2分別為大、小齒輪轉頻，Hz。

嚙合頻率：

式中：Z1、Z2分別為大、小齒輪齒數；fc為齒輪組嚙合頻率，Hz。

嚙合頻率諧頻：

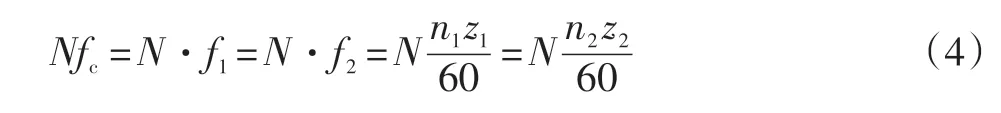
式中：N為自然數1，2，3，…，N=1時稱為基頻，即嚙合頻率f4c；N=2，3，…時，稱為二次，三次……諧波頻率。

單一（以小齒輪為例）齒輪在負載嚙合運轉中的振動信號如下。

齒輪組嚙合振動信號：

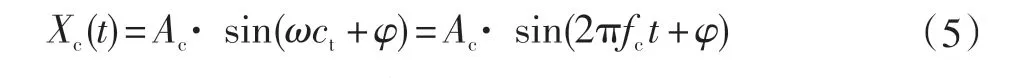
小齒輪軸轉頻振動信號：

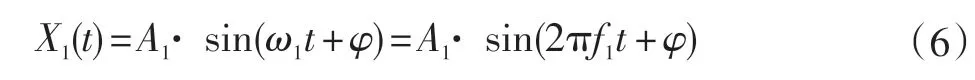
式中：Ac/A1為振動幅值；f1、fc分別為齒輪軸轉頻、嚙合頻率；φ為初相角。

因此，振動數據采集時一個簡單的齒輪嚙合運轉不可避免就會有兩個或多個振動信號。

1.2 邊頻帶頻率

圖2 所示兩個信號源被同一時刻同一通道采集、錄入，同一模數信號處理。此時就會把低頻信號疊加到高頻信號上，一般情況下高頻信號為載頻信號，低頻信號為調頻信號，調頻信號與載頻信號相互卷積作用下改變載波信號部分參數完成調制現象，改變某種參數依據就是調制信號的特征值。在齒輪嚙合傳動系統的信號中，齒輪嚙合頻率及其倍頻為較高頻率的載頻信號，單個問題齒輪軸或齒輪轉數頻率為調頻信號，則在時域波形圖上表現為高頻信號上、下峰值點連線（即低頻信號對高頻信號幅值調制的包絡線[4]）；則在頻譜圖上嚙合頻率附近產生邊頻帶結構，如圖3所示。已知包絡線峰值與間隔和邊頻帶結構與調制信號特征值有關，特征值包括：幅值A、頻率f、相位φ。下面用數學公式分別描述齒輪嚙合傳動中3種方式的調制特征。

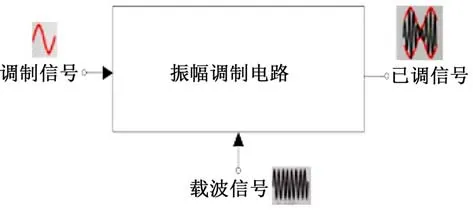
圖2 調制電路

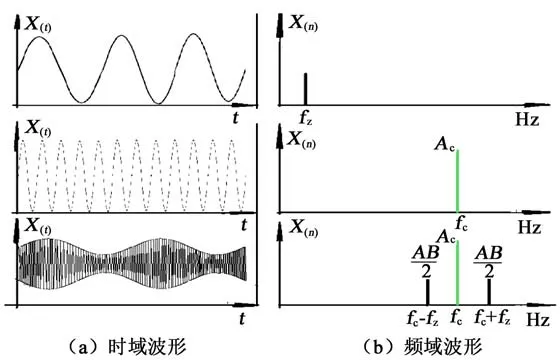
圖3 時域/頻域對應圖譜

1.2.1 幅值調制

幅值調制是根據嚙合齒面所受的交變應力引起振動信號幅度閾值發生改變的現象。例如齒輪嚙合傳動中齒輪的磨損和松動、承受的負載、齒輪偏心、齒隙過大、齒輪軸不對中等因素都會造成幅值變化的調制現象。用數學公式表述如下：

由式（5）可知，齒輪嚙合振動信號（載頻信號）為：

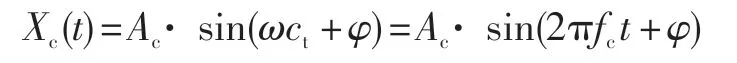
問題齒輪的調制信號：

由式（6）得：

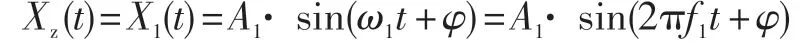
則：

則調制后的振動信號為：

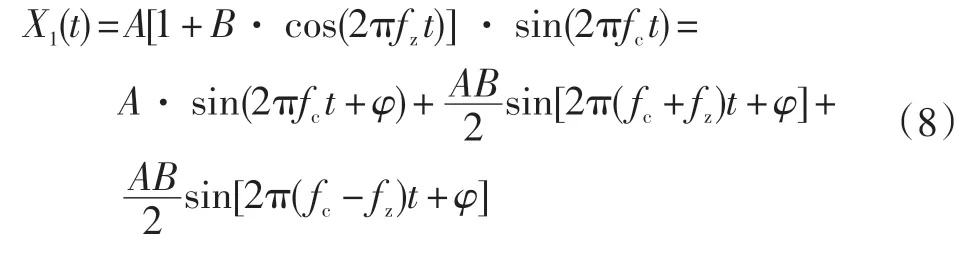
式中：A為振動幅值；B為調制系數；fz為調制頻率；fc為載波頻率。

對式（8）進行傅里葉變換，得

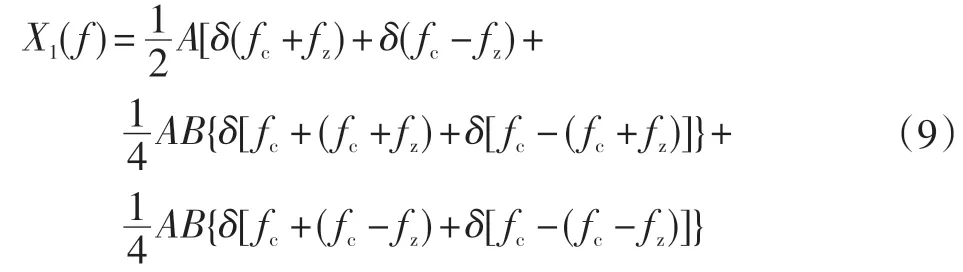
由此可見，數字信號處理[5]后頻域數學表達式（9）中，以嚙合頻率（載頻信號）fc為中心、以fz為間距均勻分布兩側的±(fc-fz)、±(fc+fz)三組頻域分量成分，與之相對應閾值分別為，即形成以基頻為中心與兩側對稱分布邊帶結構的頻譜圖[6]如圖4所示。

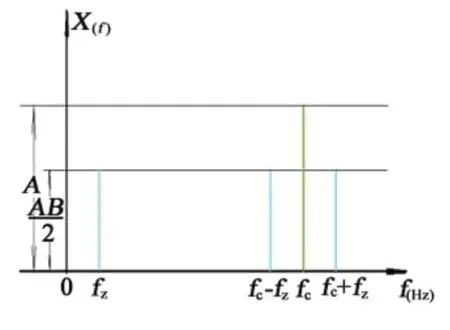
圖4 調幅信號的頻譜

這里簡要說明兩個問題：（1）幅度閾值調制后的信號能量發生了變化，如式（9）中，即反映在邊頻帶上，很明顯，幅度閾值的調制作用下增加了兩個能量分量，即基頻的左右兩側均勻分布的邊帶，其大小相等，使得總的信號能量必然增加，增加的這部分能量主要反映了幅度閾值的大小，或者說反映了故障的強弱；幅值調制邊帶的間隔寬度fz頻率反映了故障發生部件的轉頻；當調制信號有多個頻率成分的信號，則調制信號更為復雜，假如系統是線性的，每個調制信號都將會產生一對邊頻帶，如圖5所示，從而形成一個邊頻族，也會讓故障診斷帶來巨大的困難。

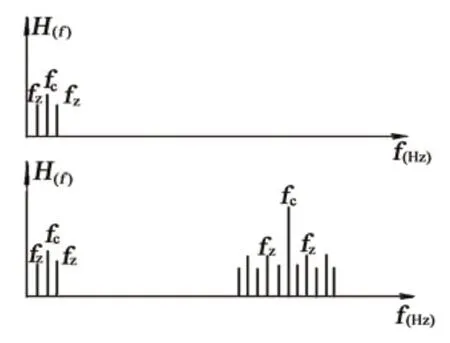
圖5 多成分調幅信號的頻譜

1.2.2 頻率調制

頻率調制效應是由于齒距周期性變化、轉速變化以及不對中引起的。事實上，一個齒輪上的載荷發生波動就會引起速度的波動，所以，常常在調幅的同時也必然會產生頻率調制效應，這里主要討論單純的頻率（即相位）調制的信號數學表達式。

當調頻信號為cos2πfZt時，調頻信號的數學表達式為：

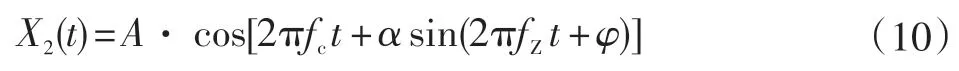
式中：A為調頻信號的幅值；a為調制系數；fZ為調制頻率；fc為載頻。

由恒等式

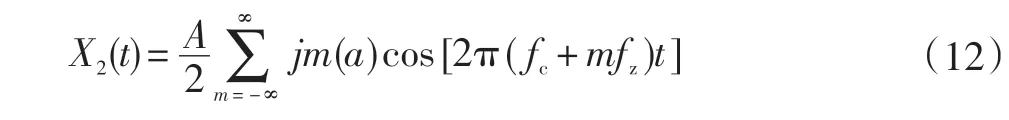
式中：jm(a)為變量a的第一類Bessel函數[7]。

對式（12）進行傅里葉變換，得：

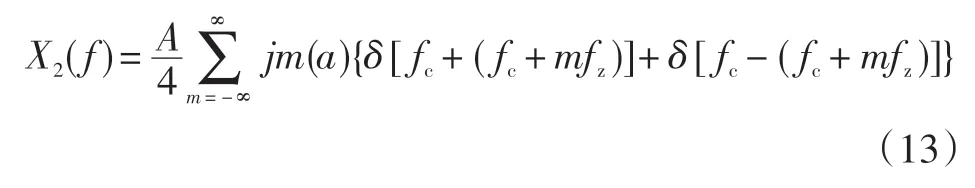
由此可見，單純頻率（相位）調制信號數字處理后，仍然以嚙合頻率（載頻信號）fc為中心，以fz頻率間隔均勻分布兩側的邊頻帶，對稱位置上的幅值也相等，如圖4所示。

1.2.3 調幅調頻共同作用下的邊頻帶

根據公式（8）、（10）得出調幅和調頻共同作用下的信號表達式[8]：

式中：A為振動幅值；B為調制系數；fz為調制頻率；fc為載波頻率；α為調制系數。

將式（14）進一步展開，得：

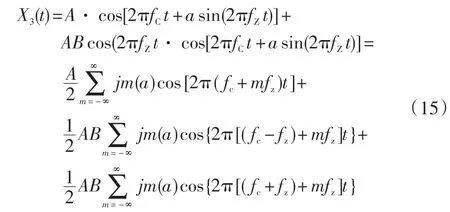
將式（15）進行傅里葉變換，得

由此可見，在幅值和頻率（相位）調制同時作用下，中心頻率fc（基頻）不再是唯一的，還包含有±(fc+fz)和±(fc-fz)兩個基頻分量，其間距都為fz的3組頻率分量進行矢量疊加，因此，調制邊頻帶就會隨著故障的隨機性而發生畸變，不再具有對稱性特征。如圖6所示。

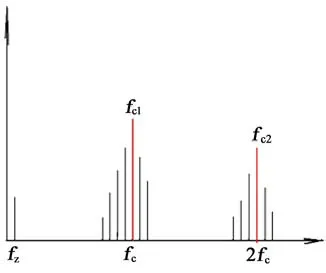
圖6 不對稱邊頻帶頻譜

2 邊頻帶不對稱性實例分析

2.1 設備概況及數據采集設計

2.1.1 設備概況

某電廠2×330 MW機組配備2×4臺低速筒式鋼球磨。電機輸入轉速為983 r/min，連接傳動方式如圖7所示。可見，一級傳動嚙合頻率為G1，其中，輸入軸轉速983 r/min，主齒輪齒數25，從動輪齒數56；二級傳動嚙合頻率G2，其中，主動輪齒數25，從動輪齒數71；三級傳動嚙合頻率G3，其中，主動輪齒數26，從動輪齒數209。

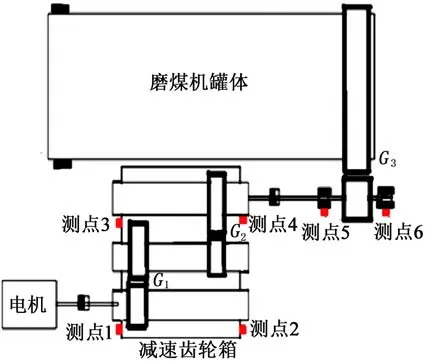
圖7 鋼球磨傳動連接方式及測點布置

根據式（4）可得：

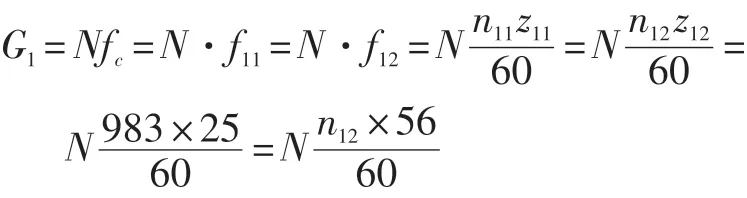
G1頻率為409.58 Hz，二倍諧頻819.16 Hz，減速箱輸出軸轉速為983 r/min，轉頻16.38 Hz，中間軸轉速為438.83 r/min，轉頻7.31 Hz。

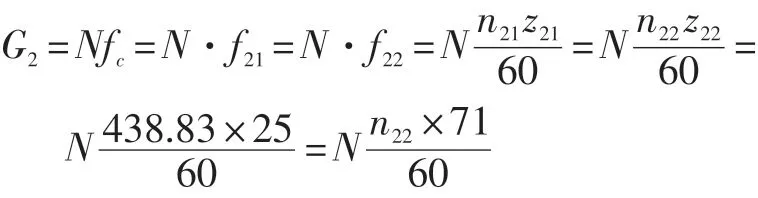
G2頻率為182.84 Hz，二倍諧頻365.699 Hz，減速箱輸出軸轉速為154.52 r/min，轉頻2.575 Hz。

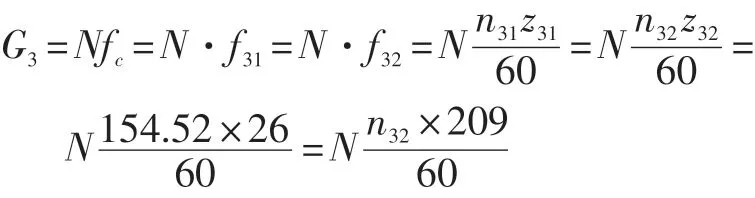
G3頻率為66.959 Hz，二倍諧頻133.918 Hz，磨煤機罐體轉速為19.22 r/min。

2.1.2 數據采集設計

由圖7可知有3個軸轉頻，在三級齒輪箱處按照圖7所示加裝6個三軸加速度振動傳感器；信號采樣頻率：低頻范圍200 Hz、高頻范圍2 000 Hz；FFT（快速傅里葉變換）[9]頻譜分析線數1 600線，解調譜分析點數1 500點。某日現場實際測得數據處理后得到的時域和頻域圖譜如圖8～9所示。

2.2 數據分析

（1）時域波形（圖8）中可清晰看到某一局部齒輪副調制信號明顯，幅值較高，說明故障到了相當嚴重的程度。低頻范圍內一個周期4 s，高頻范圍內一個周期0.4 s，（因為頻率與周期互為倒數關系）則調制信號頻率為：低頻頻率f=1/S=1/4=0.25 Hz；高頻頻率f=1/S=1/0.4=2.5 Hz，對應的軸頻率是減速箱輸出軸轉速頻率（2.575 Hz），但是這個軸左右兩側（圖7）有兩對齒輪副，嚙合頻率分別是G2和G3，因此，仍然無法準確判斷故障類型和故障發生地點。

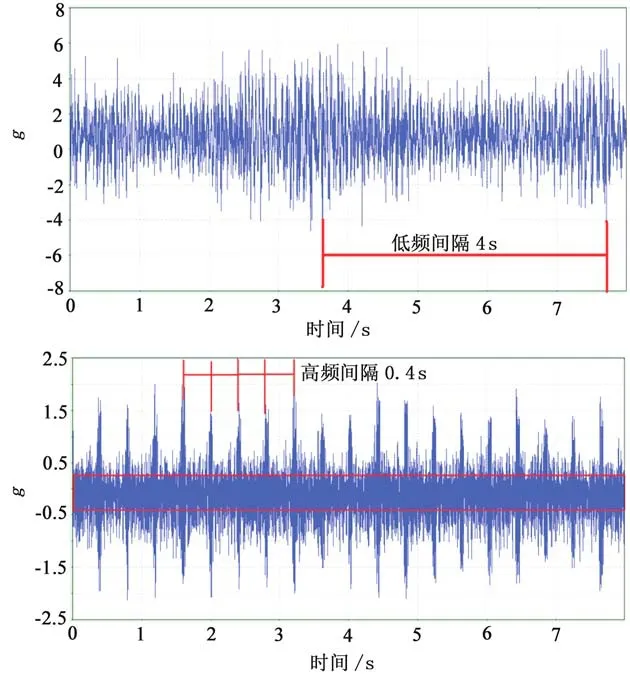
圖8 時域全景

（2）頻域圖譜（圖9）中更是難以看到對稱邊頻帶，甚至無法辨別中心頻率（即故障齒輪副嚙合頻率），因為此時邊頻帶幅值也很高，甚至高過中心頻率幅值，這只能證明故障的嚴重程度，而無法準確判斷出故障類型和故障發生地點。

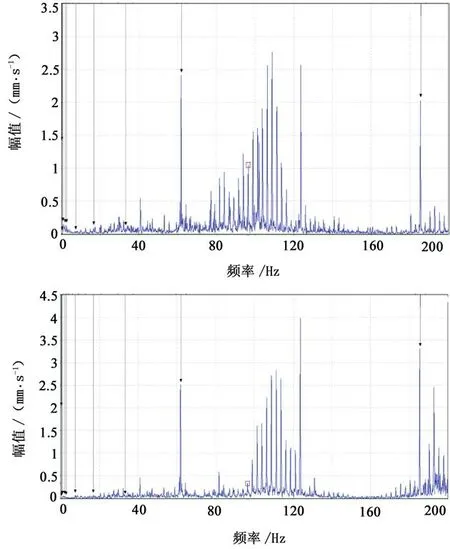
圖9 頻域全景

（3）細化頻譜、解調、倒譜等手段的定位分析。

如圖10所示，通過細化將頻譜分成三部分組成：第一部分（粉紅色區域）63.25 Hz、126.5 Hz，應該就是G3頻率與二倍諧頻，也就是故障點位置；第二部分（紅色區域）最大值位置109.31 Hz，次高值位置106.83 Hz，應該是邊頻帶區域；第三部分（藍色）184.22 Hz，應該是G2頻率。

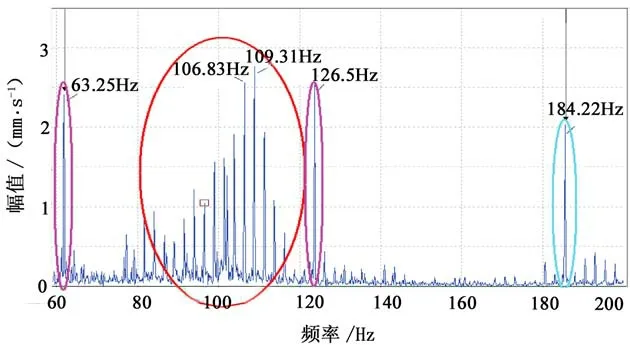
圖10 細化頻譜

如圖11所示，通過解調譜分析，最大振動幅值發生位置在G3處，由于是同軸原因影響，G2振動幅值相應增加；因此也可以證明故障點發生在G3位置。

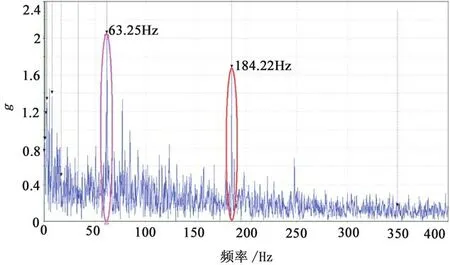
圖11 解調譜

如圖12所示，通過倒譜分析，可以很好地在頻譜圖中表現出周期分量，將特征頻譜圖中成族的邊頻帶譜線簡化成為間隔均勻的單根倒譜頻率線[10]（即圖12中紅色部分—邊頻帶），此間隔對應的頻差應該就是故障點處軸旋轉頻率。

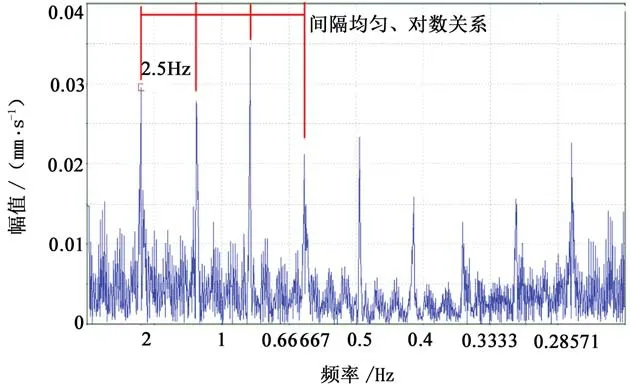
圖12 倒譜

2.3 實例驗證

現在已經排除齒輪嚴重故障時邊頻帶成族化、嚴重不對稱、偏移、幅值較基頻幅值高等等消極影響，準確判斷出故障嚴重程度及故障發生地點。磨煤機打閘停運后，解體G3處齒輪箱，發現斷齒（圖13），及時更換齒輪、恢復設備運行。

圖13 第三級傳動G3主動齒輪斷齒

綜上所述，在頻域分析中，極端的齒輪根部斷齒時會激發出1X、2X、3X嚙合頻率，甚至更多的高倍諧頻分量，且嚙合頻率及諧頻的兩側都將伴有邊頻帶成分，邊頻帶分量數目較多，幅度閾值較高，頻率范圍分布較廣，不具有對稱性，因此難以區分。只有了解數字信號處理原理，每根頻譜線對應頻率所包含的意義，通過自相關性劃分嚙合頻率及諧頻和邊頻帶，再對其進行細化分析，采用多種手段判斷和識別，才能確保診斷的準確性。

3 結束語

在齒輪傳動中，故障因素的多樣性、隨機性使得調制信號源非常的復雜，在頻率域分析過程中，多個不同頻率分量的矢量疊加組合時，產生較寬分布的密集邊頻帶。通常問題齒輪副的調制信號既有幅度閾值變化又有頻率閾值的變化，即幅、頻調制效總是同時存在，在一定的加窗函數范圍內，頻率閾值相等的等間距邊頻帶還存在著相位差，相位同方向時矢量疊加，組合邊頻帶幅值增大；反之，組合邊頻帶幅值減小。因此形成了不對稱分布的邊頻帶，給故障診斷分析過程中帶來極大的困難。考慮到邊頻帶對故障類型和故障嚴重程度的指向性，如何消除不對稱邊頻帶在故障診斷的影響就變得尤為重要。只有通過產生機理上入手，細化并且區分每根邊頻帶頻率和幅值意義才能作出故障診斷結論，而這種診斷結論還是不確定的，還需要采用綜合的多種手段故障特征識別，才能作出精準故障診斷結論。