多柔體車輛耦合系統對動力學性能的影響
明鑒,石姍姍,陳秉智
(大連交通大學 機車車輛工程學院,遼寧 大連 116028)*
隨著鐵路車輛運行速度的不斷提高,車輛設計輕量化等發展迅速,使得車輛結構剛度降低,且運行條件逐漸嚴苛,故不能忽視軌道車輛關鍵結構因非線性變形對車輛系統振動所帶來的影響[1].采用單一的剛體動力學建模方式來研究鐵路車輛的動力學特性已經不能滿足科研需要,有必要將柔性體動力學引入到多體動力學仿真計算中.郭訓等[2]研究了柔性輪對對車輛動力學的影響;吳少培等[3]探討了構架柔性對車輛振動特性的影響;楊丹丹[4]基于SIMPACK的某型列車柔性車體剛柔耦合建模進行研究其對動力學性能的影響等,皆分析得出,和剛性模型對比,采用柔性體建模方式對列車的運行表現仿真結果存在一定影響,且更能表現列車真實的運行狀態,所以有必要將列車關鍵結構建立為柔性體.考慮到單一結構柔性化不能反映真實的多柔性體耦合在現實場景中的表現[5].為了研究多柔體耦合車輛系統和多剛體車輛系統的整體差異,本文在已有的對單一柔性結構進行研究的理論基礎之上,將柔性輪對、柔性構架、柔性車體共同組建一個多柔體動力學系統耦合模型,仿真分析剛柔耦合車輛模型和多剛體車輛模型在運行狀態下,相關動力學指標的差異.
1 車輛系統動力學相關指標
軌道車輛系統動力學性能的評價主要通過車輛在運行時的穩定性、平穩性和曲線通過性能等指標綜合評估.
1.1 車輛運行穩定性指標
車輛運行穩定性評價采用非線性臨界速度方法,讓車輛在時域中以一定速度通過一段有激勵的線路,然后讓車輛在撤銷激勵的光滑線路上繼續運行,根據輪對橫移量是否收斂來判斷當前速度是否達到蛇形運動失穩時的臨界速度[6].
1.2 車輛運行平穩性指標
車輛在運行中會產生各種形式的振動,對于客運列車來講,振動在一定程度上影響了旅客乘坐的舒適性.我國對鐵路車輛運行平穩性評價分別按照車體振動加速度(av為垂向振動加速度,al為橫向振動加速度)和Sperling平穩性指標來評定[7],具體評價等級見表1.
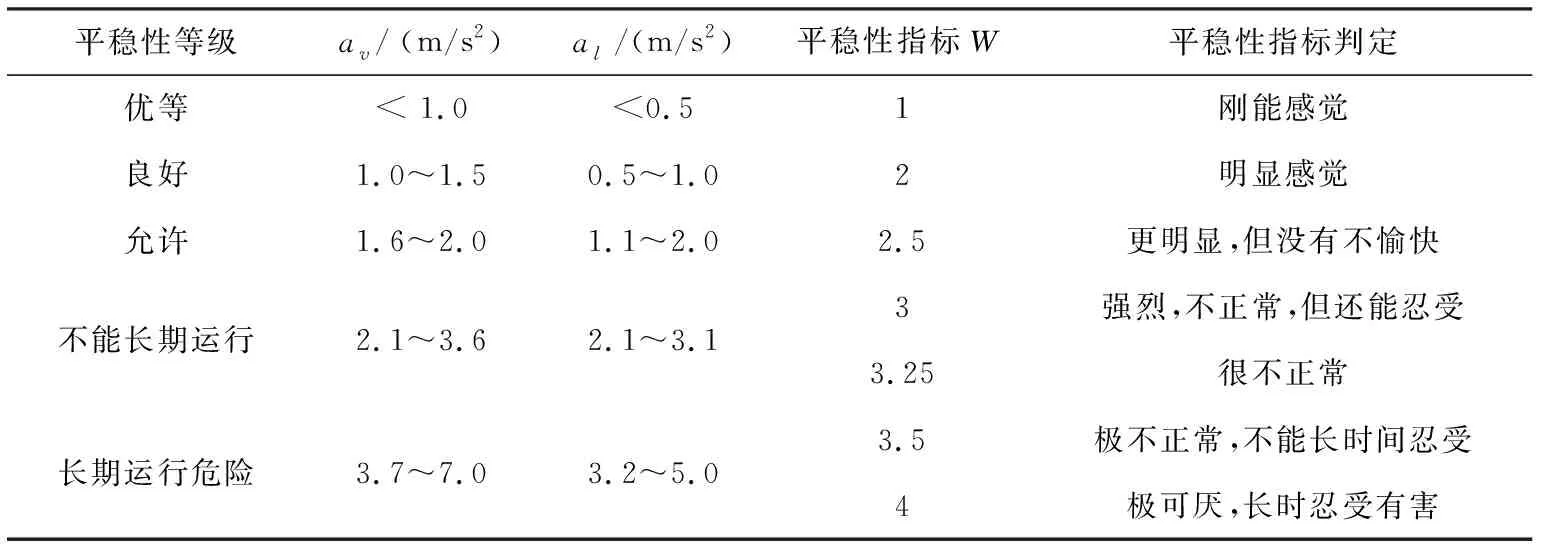
表1 客車運行平穩性評價標準
其中Sperling平穩性指標的評價方法如下:
式中,a為車體振動加速度(cm/s2),f為車體振動頻率(Hz),F(f)為與振動有關的修正系數,W為評價指標.
垂向振動不同頻率下的修正系數F(f)取值:
橫向振動不同頻率下的修正系數F(f)取值:
1.3 曲線通過性能
為了判斷車輛過曲線線路運行時所產生脫軌現象的受力情況,并找出臨界條件,目前我國主要采用脫軌系數和輪重減載率對車輛曲線通過性能進行評價[8].
1.3.1 脫軌系數
根據我國95J01-M《高速試驗列車客車強度及動力學性能規范》,對高速動車組的脫軌系數定義為[9]:
式中,Q1為作用于輪緣上的側向力,P1為作用于車輪上的垂向力,μ1為輪緣與鋼軌之間的摩擦系數,α1為輪緣角.
參考95J01-M中的脫軌系數安全范圍為:
Q1/P1≤0.8
1.3.2 輪重減載率
主要對于一側車輪嚴重減載時所造成的脫軌現象進行評價,對輪重減載率的定義如下[10]:
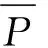
根據95J01-M中采用的輪重減載率安全指標為[11]:
ΔP/P≤ 0.6
2 車輛系統動力學建模
2.1 多剛體車輛模型建立
多剛體車輛的建立主要在SIMPACK軟件中,建立輪對子結構,車輪踏面型號采用S1002型號;剛性轉向架結構由搖枕、構架、前后輪對和軸箱組成,構架和輪對之間有一系軸箱彈簧、一系減振器和軸箱轉臂,搖枕和構架之間建立了二系空氣彈簧、抗蛇形減振器、二系橫向減振器以及抗側滾扭桿結構;根據車輛的實際參數,構建車體結構,并將轉向架子結構與車體之間通過虛搖枕進行裝配,組建最終的多剛體車輛模型,如圖1所示.
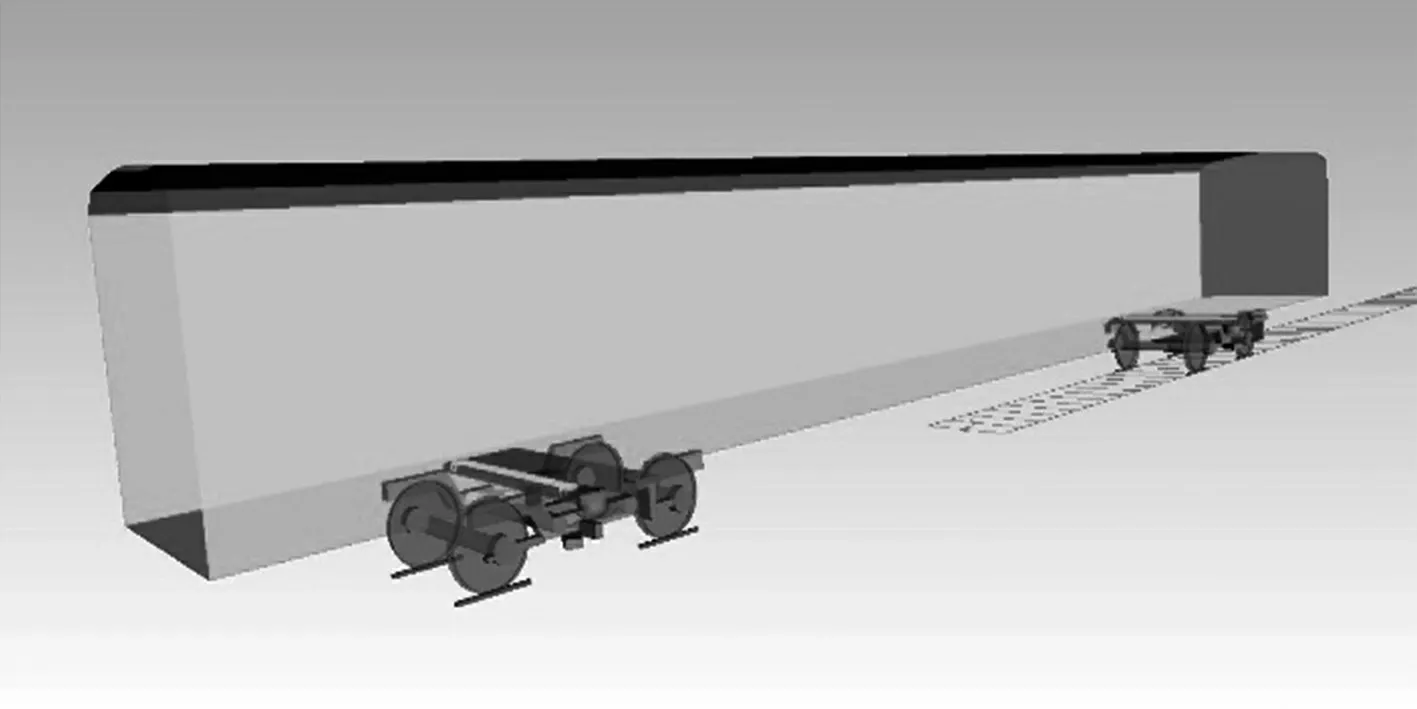
圖1 多剛體車輛模型示意圖
2.2 剛柔耦合車輛模型建立
在SIMPACK軟件中建立柔性體,需要作為SIMPACK和其他有限元軟件之間的FEMBS接口程序進行轉換.主要通過將有限元分析的物理模型特征等數據輸入到運動方程,形成柔性體數據的標準輸入數據文件格式(SID文件).然后將SID文件通過FEMBS接口程序的FEM模塊寫入,并同時將柔性數據轉化成SIMPACK可讀格式.從而在SIMPACK軟件中得到可使用的柔性體文件.
剛柔耦合模型的建立主要建立柔性輪對、柔性構架、柔性車體結構.文中的柔性結構建模流程為根據實際結構參數采用SolidWorks幾何建模,HyperMesh有限單元網格劃分,并通過有限元軟件ANSYS進行有限元結構的子結構分析和模態計算,將生成.sub、.cdb、.tcms文件導入到 SIMPACK軟件的FEMBS接口生成柔性體文件.圖2為柔性體建模流程操作示意圖.

圖2 柔性體結構建模流程
最后用生成的輪對、構架、車體的柔性體結構取代對應的剛性結構,組建剛柔耦合車輛模型,如圖3所示.

(a)柔性輪對結構 (b)柔性構架結構
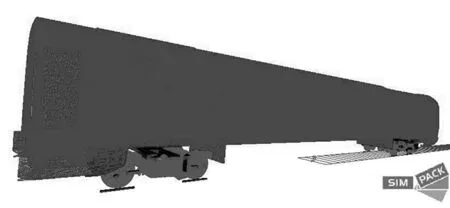
(c)剛柔耦合車輛模型圖3 剛柔耦合車輛模型示意圖
為了保證所建立的車輛模型系統的平衡以及模型的可靠性,最后在建立完成的模型基礎上進行Preload名義力計算,以確保車輛系統處于平衡穩定狀態.
2.3 軌道參數
本文采用軌道型號為UIC定義的60 kg/m 型號鋼軌,軌距為1 435 mm,軌底坡為1∶40.車輪型面為歐洲鐵路標準型面S1002.所采用的軌道不平順激勵為京津線實測軌道譜.
臨界速度指標計算采用的線路參數為直線,在30~1 000 m處加入軌道不平順激勵,1 000 m以后撤銷激勵.
在分析車輛其他動力學指標的差異時,設置分別加載京津線實測軌道激勵譜的直線和曲線兩種軌道類型.其中曲線軌道設置參數:緩和曲線長度為550 m,曲線長度為400 m,半徑為6 000 m,外軌超高為0.11 m.
3 仿真流程
根據車輛系統動力學相關指標類型,將車輛的運行工況分為直線工況和曲線工況兩種.為研究車輛在相同運行條件、不同速度下的運行狀態,在直線運行條件下,仿真速度區間為160~ 360 km/h,每隔10 km/h為一個采樣速度,共計21個計算工況.在曲線運行條件下,仿真速度區間為200~300 km/h,每隔20 km/h為一個采樣速度,共計6個計算工況.將多剛體車輛模型和剛柔耦合車輛模型分別在上述工況進行仿真計算,根據計算結果進一步評價兩種建模方式對動力學性能的影響.
4 仿真計算結果分析
4.1 臨界速度
通過非線性臨界速度仿真方法,多剛體車輛模型的臨界速度計算結果為483 km/h,剛柔耦合車輛模型的臨界速度結果為432 km/h,臨界速度低于剛性模型約10.56%.如果采用多剛體模型代替剛柔耦合模型,則會使得車輛穩定性計算結果偏大,實際情況會有一定失穩風險.
4.2 車輛運行平穩性指標差異
4.2.1 車體加速度
在車體加速度方面整體上隨著運行速度的增加,呈現增大趨勢.剛柔耦合車輛模型的車體加速度在橫向和垂向的值皆大于多剛體車輛模型.由于采用的車輛為高速動車組,且仿真速度皆在安全行駛速度范圍內,所以在仿真的速度區間內,車體質心加速度表現等級為優.
在直線運行條件下,橫向車體質心加速度,如圖4(a),在運行速度增加的條件下,兩者的差距逐漸縮小.差距最大時在運行速度為160 km/h,剛柔耦合車輛模型比多剛體車輛模型車體橫向加速度大0.12 m/s2.垂向車體質心加速度結果顯示,如圖4(b),在運行速度增加的情況下,兩者的差距在逐漸增大.差距最大時的運行速度為350km/h,剛柔耦合模型比多剛體模型車體垂向加速度大0.124 m/s2.

(a)車體橫向加速度
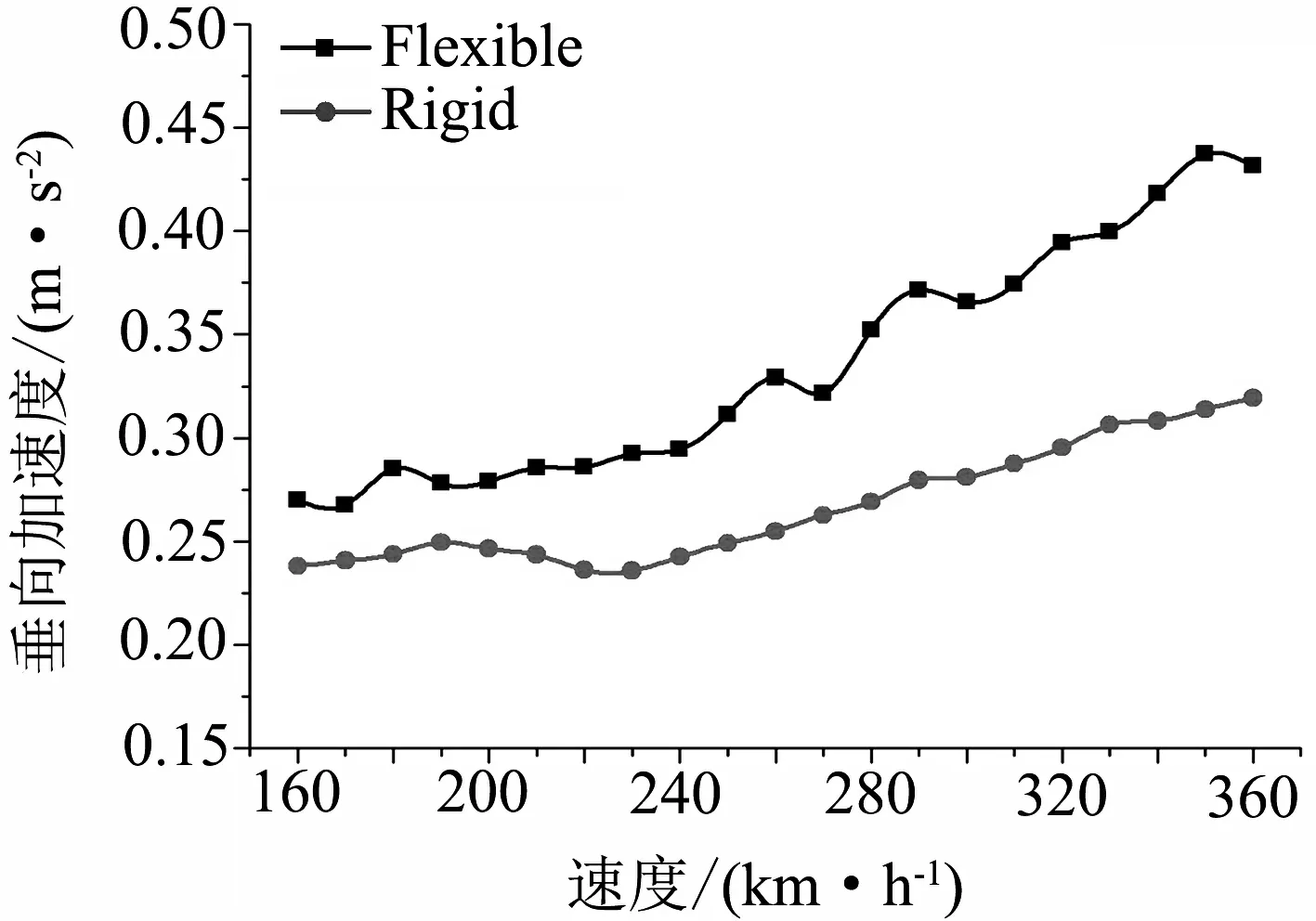
(b) 車體垂向加速度圖4 直線運行條件下車體加速度曲線
同樣,在曲線運行條件下隨著運行速度增加,橫向車體質心加速度,如圖5(a)所示,兩者的差距在逐漸減小.差距最大的時候在運行速度為200 km/h時,剛柔耦合模型比多剛體模型車體橫向加速度大0.119 m/s2.垂向車體質心加速度,如圖5(b)所示,兩者的差距在逐漸增大.差距最大時的運行速度為280 km/h,剛柔耦合模型比多剛體模型車體垂向加速度大0.085 m/s2.

(a) 橫向加速度
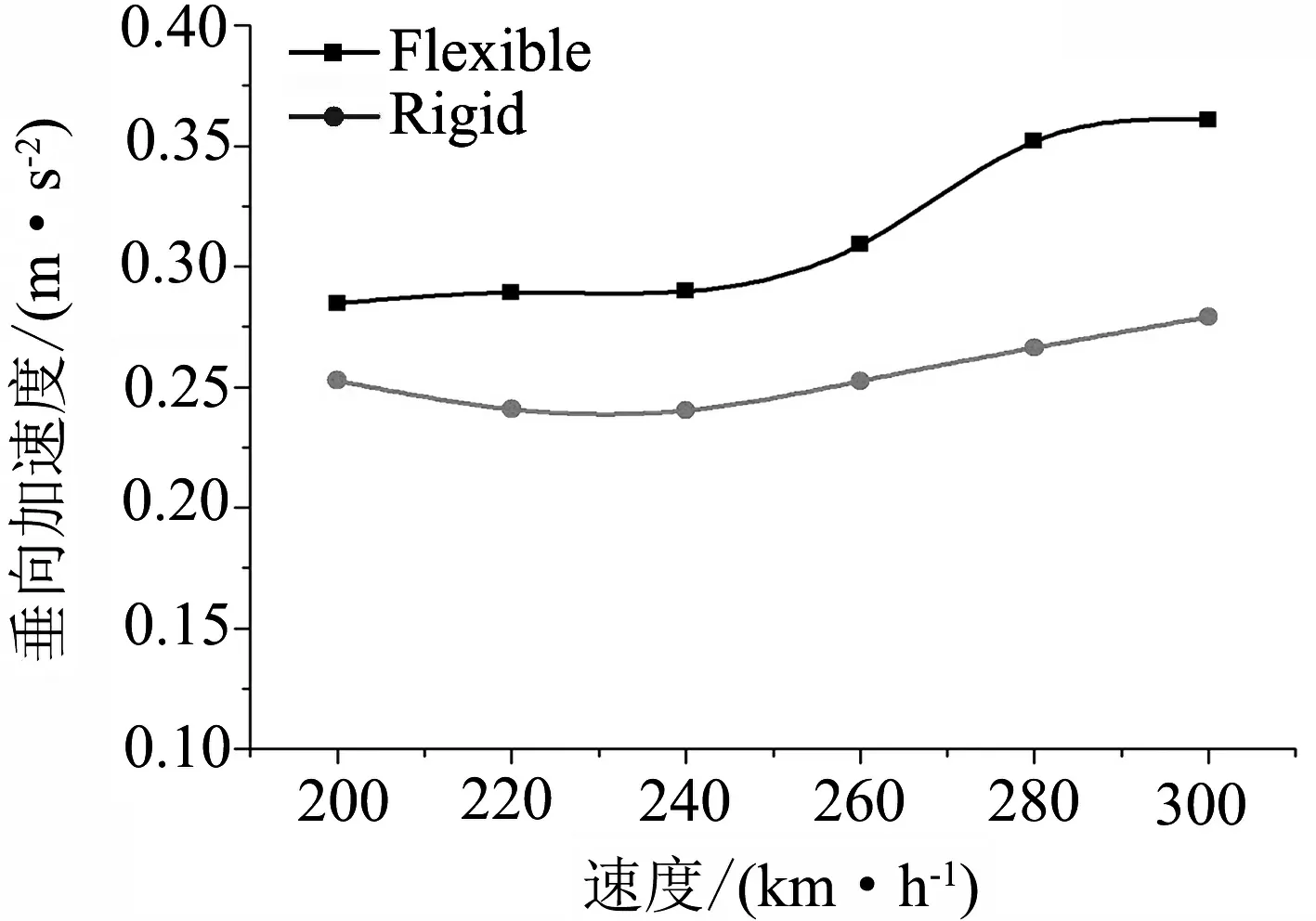
(b) 垂向加速度圖5 曲線運行條件下車體加速度曲線
4.2.2 Sperling平穩性指標
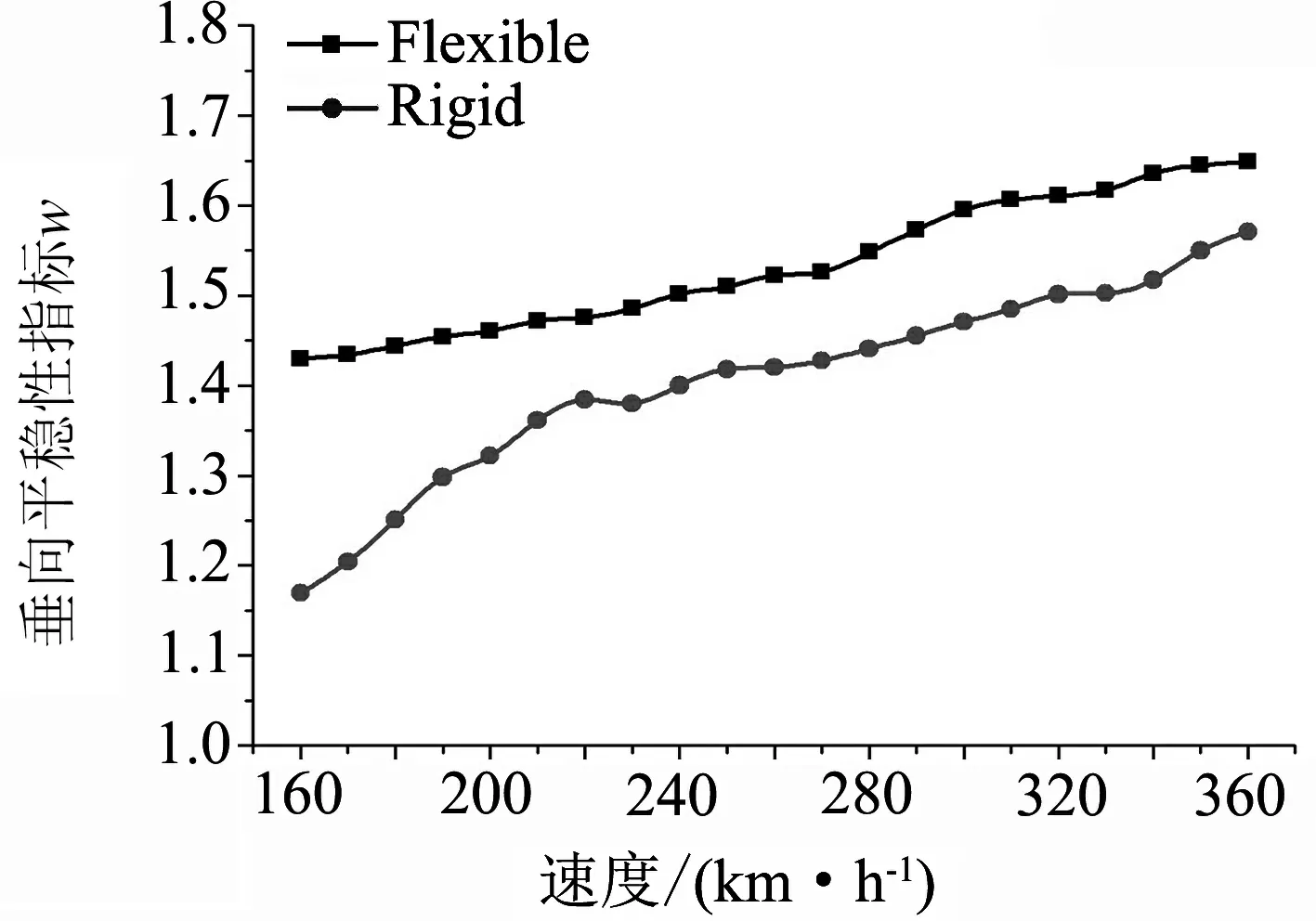
由于和短期內的舒適度考核指標“車體質心加速度”相比,對于長時間車輛運行對乘客產生的影響,Sperling平穩性指標中增加了加速度的幅值以及振動頻率的影響.從仿真結果來看,車輛平穩性整體表現隨著速度的增加而變差,其中剛柔耦合模型相對比多剛體模型表現不佳.
如圖6(a)所示,為橫向平穩性指標對比;如圖6(b)所示,為垂向平穩性指標對比.
(a) 橫向平穩性指標對比
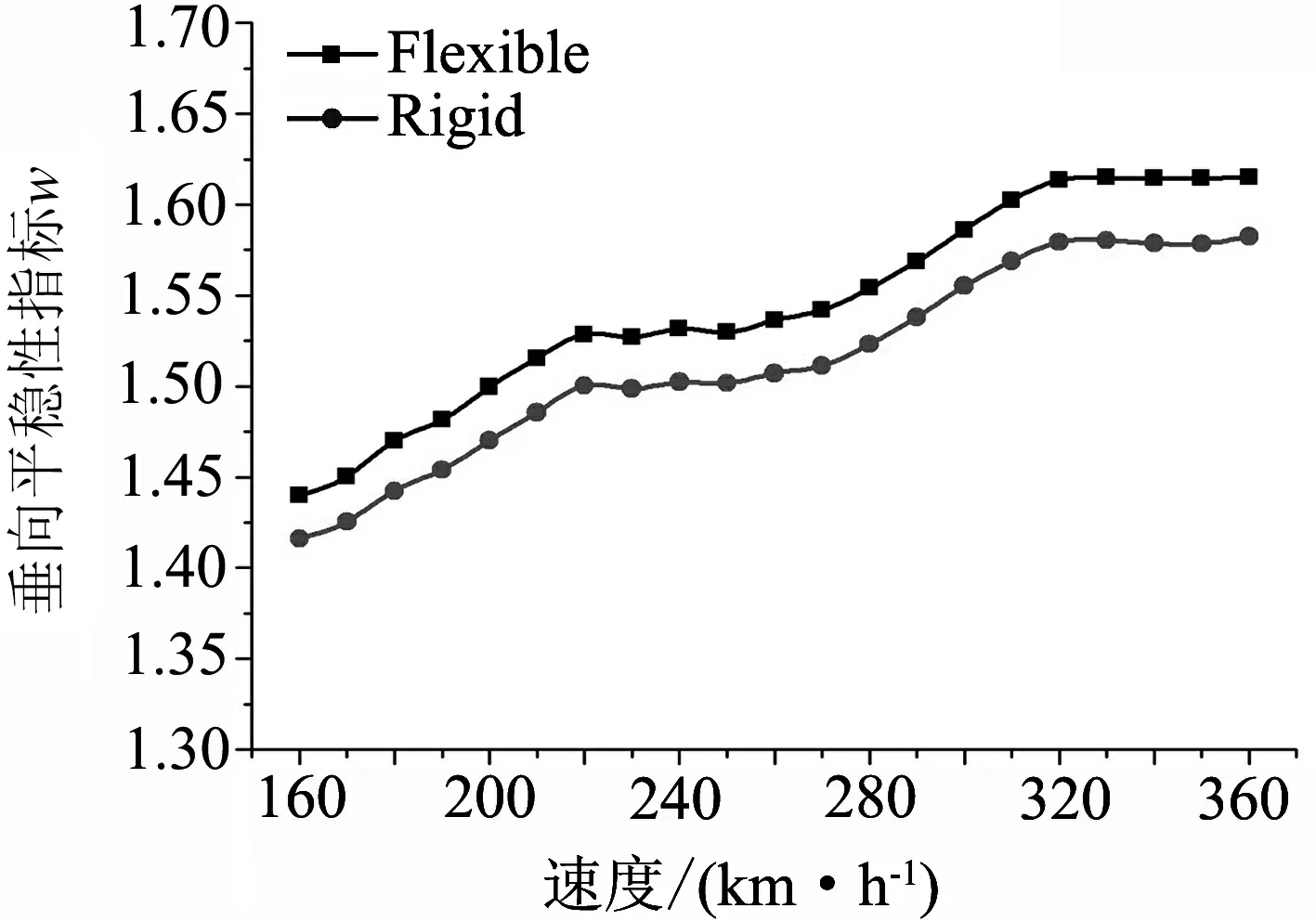
(b) 垂向平穩性指標對比圖6 車輛在直線運行狀態下的Spling平穩性指標對比
4.3 曲線通過性能分析
4.3.1 脫軌系數
在仿真的6個速度工況,由于時速的不同導致輪軌之間作用效果也不同.如圖7所示,最明顯的表現為在240 km/h之前,作用于輪緣上的側向力為正,由于時速的提高,離心力作用導致輪緣側向作用力逐漸減小,并最終改變方向作用于軌道曲線半徑內側,并隨之在速度增加的趨勢之下,脫軌系數不斷增加.但在計算的六個速度指標中,所得出的每個工況內最大脫軌系數,除了在200 km/h兩者接近以外,剛柔耦合模型皆大于多剛體模型.
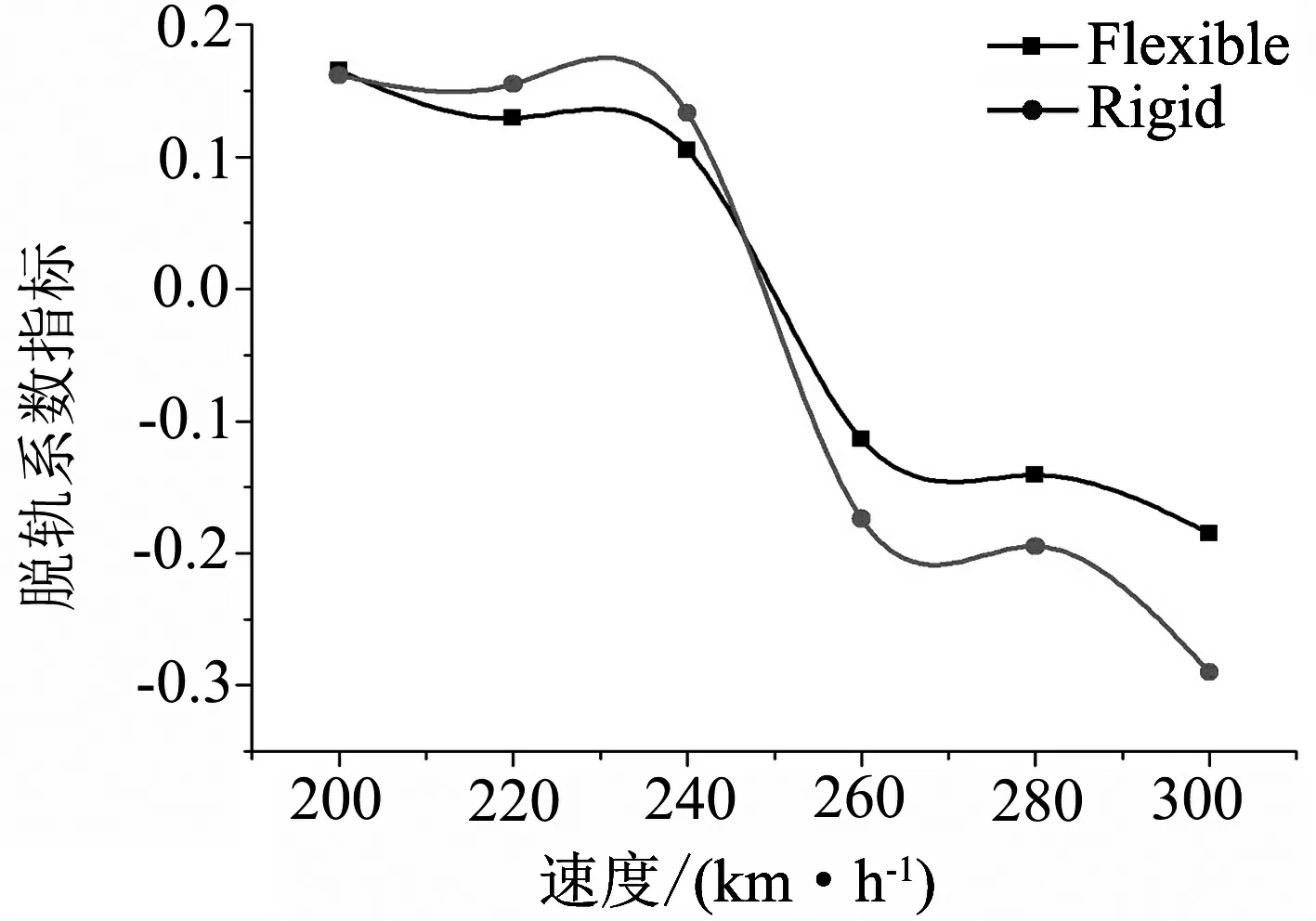
圖7 脫軌系數指標對比
4.3.2 輪重減載率
對于輪重減載率的計算分析中,多剛體模型和剛柔耦合模型分別針對每個輪對為一個觀測點,分為前后轉向架的前后輪對,一共8組數據,如圖8所示(注:ff表示前轉向架前輪對;fr表示前轉向架后輪對;rf表示后轉向架前輪對;rr表示后轉向架后輪對).
通過計算結果可以發現,整體趨勢,相同速度等級下,剛性模型整體比柔性模型輪重減載率數值小.剛柔耦合模型,最先到允許限度0.6為后轉向架第二輪對.且在時速260 km/h以后,在曲線上表現不佳,有一定脫軌傾覆風險.多剛體模型,同樣最先到允許限度0.6為后轉向架第二輪對.且在時速280 km/h以后,在曲線上同樣表現不佳.
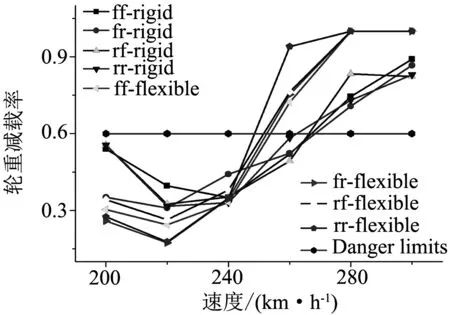
圖8 輪重減載率指標對比
5 結論
本文通過建立多剛體車輛模型和剛柔耦合車輛模型進行仿真分析,研究了多柔體結構耦合系統在軌道車輛模型運行時對動力學指標的影響.結果表明:
(1)臨界速度指標中,剛柔耦合車輛模型的臨界速度相比于多剛體車輛模型降低了10.56%,采用多剛體車輛模型作為結果參考,會高估車輛在運行時刻的極限表現;
(2)在車體加速度、車輛運行品質以及舒適度指標中,剛柔耦合車輛模型仿真結果高于多剛體車輛模型,表明考慮結構的柔性變形和整體的耦合效應導致車輛平穩性指標的表現更加危險;
(3)車輛曲線通過性能指標中,剛柔耦合車輛模型相比于多剛體車輛模型仿真結果顯示,剛柔耦合模型對于曲線通過能力欠佳,尤其運行速度在260 km/h以上時,兩者曲線通過性能的差異隨速度的增加呈現逐漸增大的趨勢.
因此,軌道車輛系統動力學在某些場景中將結構簡化為剛性體結構可能會高估車輛運行時的真實表現,從而對后期的判斷以及決策產生一定的風險.若對仿真結果允許誤差較小,結果需求較精準,建議采用多結構柔性化處理的剛柔耦合建模方式進行仿真計算.

