自由液面處雙懸停氣泡破裂聲特性研究

叢山昊，劉競婷，2，王貴超，2，孫遜，2，陳頌英，2

（1山東大學(xué)機(jī)械工程學(xué)院，山東濟(jì)南250061；2山東大學(xué)高效潔凈機(jī)械制造教育部重點實驗室，山東濟(jì)南250061）

引 言

氣泡與自由液面相互作用現(xiàn)象廣泛存在于自然界、國防、核工業(yè)、船舶與海洋工程等多個領(lǐng)域。例如，風(fēng)成氣泡在海面破裂形成的氣溶膠對海洋-大氣生態(tài)系統(tǒng)的物質(zhì)交換及全球氣候具有較大影響[1-2]。氣泡破裂過程亦是核電站蒸汽發(fā)生器蒸汽夾帶液滴的主要來源方式之一，對核電站防事故系統(tǒng)開發(fā)與優(yōu)化意義重大[3]。此外，可燃冰開采、船舶減阻、尾流降噪等海洋工程與氣泡破裂過程息息相關(guān)[4]。關(guān)于氣泡破裂的機(jī)理研究已經(jīng)涵蓋了各個方面，但針對氣泡破裂引起液面波動輻射聲壓特性的研究目前還是一個比較新穎的方向，對于探究氣泡與液面相互作用聲特性表征、界面聚合遷移與聲特性的內(nèi)在關(guān)系、及被動聲學(xué)測量技術(shù)的發(fā)展具有重要的應(yīng)用價值。

自由液面氣泡破裂行為差異與多種因素有關(guān)。一方面，大量學(xué)者研究表明，氣泡在自由液面處的碰撞與破裂行為取決于氣泡碰撞前的上升特性，例如氣泡形態(tài)和終端速度[5-7]等。然而，上升特性取決于氣泡自噴管脫離的狀態(tài)，Kulkarni等[8]系統(tǒng)地總結(jié)了氣泡自噴管脫離形成和上升速度的研究成果。自Woodcock等[9]發(fā)表了氣泡液面破裂的研究成果以來，學(xué)者們在氣泡破裂成因、射流和噴射液滴形成機(jī)理、界面奇異性探究等方面做了大量工作，從多角度揭示自由液面氣泡破裂過程。Israelachvili[10]認(rèn)為氣泡液膜減薄至臨界厚度，熱波動或London-van der Waals力等微小擾動會導(dǎo)致液膜破裂。Poulain等[11]建立了廣義的氣泡液帽模型，進(jìn)一步驗證了Israelachvili的結(jié)論。在Blanchard等[12]提出了液膜滴和噴射液滴的概念后，學(xué)者們進(jìn)一步探究了射流和噴射液滴生成機(jī)理，例如，Blake等[13]采用邊界積分法模擬氣泡液面破裂過程，計算了射流和噴射液滴形成時的液體夾帶率。Duchemin等[14]對氣泡自由液面破裂進(jìn)行了全面研究，數(shù)值模擬結(jié)果表明高速射流是由聚焦毛細(xì)波引起的空腔自相似坍塌產(chǎn)生的，較好解釋了射流產(chǎn)生的原因。但由于當(dāng)時定量實驗數(shù)據(jù)較少，實驗驗證主要停留在定性分析上。Zeff等[15]的工作起到了關(guān)鍵性的作用，通過實驗證明了射流是由自由液面的奇異變形引起的，氣液界面形狀在射流產(chǎn)生前的瞬間形成了極高的曲率。這種奇異現(xiàn)象是由液體的慣性和表面張力共同驅(qū)動的，并最終在黏度的影響下消失。隨后，Brenner[16]對奇異性進(jìn)行了拓展研究。在大量分析前人實驗和數(shù)值模擬研究結(jié)論的基礎(chǔ)上，Deike等[17]提出了一個預(yù)測全參數(shù)范圍內(nèi)射流速度的唯象公式，為計算射流速度提供了方法。此外，射流斷裂產(chǎn)生的噴射液滴、氣泡破裂行為測量技術(shù)也得到學(xué)者們的廣泛關(guān)注，Walls等[18]討論了重力和黏度對噴射液滴產(chǎn)生的影響。MacIntyre等[19]分析了噴射液滴產(chǎn)生初期的形態(tài)特性。Nikolov等[20]采用壓電聲法監(jiān)測氣-水界面氣泡破裂現(xiàn)象。虞想等[21]總結(jié)了自由液面氣泡破裂行為的測量方法和經(jīng)驗公式。

近些年來，聲發(fā)射技術(shù)因其非接觸、精度高等優(yōu)點，在科研和生產(chǎn)生活中發(fā)揮著越來越重要的作用[22-23]。氣泡聲特性作為氣泡運動學(xué)表征的重要手段[24-25]，在氣泡液面相互作用與宏觀現(xiàn)象之間搭建了橋梁。最早的氣泡聲學(xué)研究可追溯到20世紀(jì)30年代，Minnaert[26]是率先研究水下浸沒排氣振動發(fā)聲的學(xué)者之一，通過實驗和公式推導(dǎo)，發(fā)現(xiàn)氣泡微小線性振動的固有頻率f與其半徑r成反比，式(1)就是著名Minnaert頻率公式：

式中，k為氣體比定壓和比定容熱容之比；p為流體靜壓力；ρ為液體密度。

此后，Strasberg[27]、Lamb[28]、Longuet-Higgins[29]嘗試建立了理想氣泡與畸變氣泡形態(tài)變化同聲輻射間的內(nèi)在聯(lián)系，使得聲信號表征氣泡形態(tài)變化成為可能。Longuet-Higgins[30]在分析雨滴落至水面過程時，分析歸納了氣泡徑向振蕩激發(fā)的原因，進(jìn)一步揭示了氣泡振蕩與壓力、形態(tài)、速度場之間的關(guān)系。在聲特性表征氣泡形態(tài)研究的基礎(chǔ)上，學(xué)者們逐步關(guān)注氣泡在自由液面破裂的聲規(guī)律[31]，開展氣泡云和氣泡群振蕩機(jī)理研究。Yoon等[32]通過氣泡柱實驗，論證了海洋環(huán)境噪聲（小于1 kHz）是由風(fēng)造成的。鄧巍等[33]采用頻譜分析法對三種縱橫比條件下的氣泡羽流進(jìn)行研究，發(fā)現(xiàn)壓強(qiáng)越大，氣泡羽流的振動峰值和頻率越小。但由于氣泡群形成與作用較為復(fù)雜，這一領(lǐng)域研究發(fā)展緩慢。學(xué)者們重點研究了雙氣泡、多氣泡聚并及破裂聲特性規(guī)律。Shima[34]推導(dǎo)出兩球形氣泡在不可壓縮液體中的振蕩固有頻率公式。Manasseh等[35]利用水聽器對氣泡鏈周邊的聲壓進(jìn)行測量，分析脈沖波形沿氣泡鏈方向的變化，認(rèn)為聲場具有很強(qiáng)的各向異性。Roshid等[36]通過測量氣泡的發(fā)射頻譜來預(yù)測氣泡的大小和相互作用氣泡的數(shù)目。雖然對于氣泡破裂過程與聲信號整體特性的研究較多，但氣泡破裂及液面波動的聲壓特性規(guī)律尚不明確，因此，本文以自由液面雙懸停氣泡為研究對象，研究了氣泡在自由液面破裂的過程，及引起液面波動重疊現(xiàn)象與聲疊加特性的內(nèi)在聯(lián)系。

1 實驗裝置和方法

1.1 實驗裝置

本文所采用的實驗裝置如圖1所示，由氣泡生成系統(tǒng)、圖像采集系統(tǒng)和聲信號采集系統(tǒng)三部分組成?？諝庥勺⑸浔茫?00 ml）提供，通過氣體管路、噴管（r=1 mm，出口氣速約為0.58 m/s）進(jìn)入可視化的有機(jī)玻璃容器，容器設(shè)計足夠大，尺寸為0.3 m×0.3 m×0.5 m，水箱壁邊長超過20個毫米級氣泡直徑[37]，避免限制區(qū)域內(nèi)的混響效應(yīng)對有效聲波的干擾。容器內(nèi)液體介質(zhì)為靜置后的自來水，液位高度為80 mm，溫度20℃。為了實現(xiàn)自由液面處懸停氣泡的動態(tài)行為捕捉，設(shè)置高速攝像機(jī)幀頻為1295 fps，圖像分辨率為1280×720 pixel/cm2。聲信號采集系統(tǒng)采用了兩個水聽器（TC4013），分別布置于管口與自由液面處，分別為與管口在同一水平面且距離管口中心10 mm處、靠近自由液面且距離噴管中軸線20 mm處，水聽器位置如圖所示；水聽器采集到的聲壓脈動信號通過信號采集儀轉(zhuǎn)換為電壓信號，并保存至計算機(jī)。為了實現(xiàn)流動視頻圖像與聲音信號的同步采集，采用電壓觸發(fā)（1 V），設(shè)計同步觸發(fā)器，分別連接高速攝像機(jī)和信號采集儀的觸發(fā)接口。

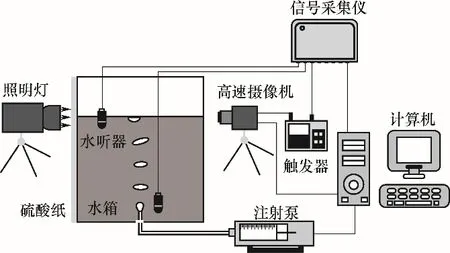
圖1 實驗裝置示意圖Fig.1 Schematic diagram of experimental apparatus

表1為氣泡破裂聲信號實驗測量裝置水聽器精度不確定性因素分析，由表可知，水聽器靈敏度為-209.9 dB，誤差值為-0.2 dB，偏差率為0.095%；頻率范圍為1~1×105Hz。根據(jù)聲壓級SPL與聲壓P的關(guān)系式：

表1 實驗裝置水聽器精度不確定性因素分析Table 1 Analysis of uncertainty factors of hydrophone precision in experimental equipment

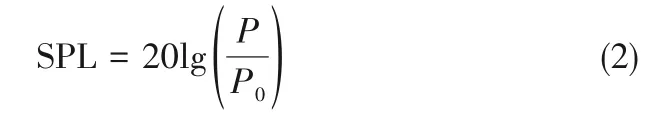
式中，P0為水中基準(zhǔn)聲壓10-6Pa，由式（2）可知-0.2 dB轉(zhuǎn)化為聲壓僅為9.77×10-7Pa，下文涉及聲壓變化最小值為0.17 Pa，遠(yuǎn)大于不確定度對應(yīng)的聲壓，故水聽器精度不確定度可以忽略不計，實驗中測量的結(jié)果具有較高的可靠性。

1.2 實驗方法

1.2.1 信號時頻處理方法 波形分析是通過分析波譜曲線形態(tài)，提取表征曲線形態(tài)參量的一種常用方法，可分為時域分析和頻域分析。時域分析是基于時間域獲取波形特征參數(shù)，頻域分析是建立在傅里葉變換[式（3）]基礎(chǔ)上，運用數(shù)字轉(zhuǎn)換方法獲取頻域特征。

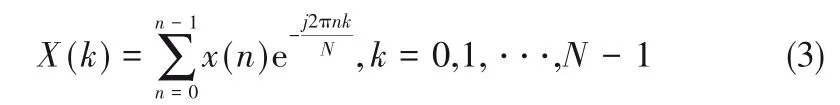
式中，x(n)為時域采樣的信號序列；N為窗函數(shù)長。

本實驗采用短時傅里葉變換的時頻分析技術(shù)，利用Hamming窗（窗長512、窗函數(shù)重疊率50%）對實驗音頻信號進(jìn)行分段，識別出聲信號中心頻率段。圖2所示1 s內(nèi)氣泡產(chǎn)生過程的時-頻譜圖和三個特征時刻的聲壓時域脈動波形，可以看出，在2.071、2.474、2.9 s三個特征時刻，氣泡振動輻射聲壓頻譜中心頻率為1336 Hz左右，氣泡生成過程的聲壓時變曲線形同衰減的正弦波。

圖2 氣泡產(chǎn)生過程時-頻譜圖與三個特征時刻的聲壓時域脈動波形Fig.2 Time-frequency spectrum of bubble generation process and time-domain pulsation waveform of sound pressure at three characteristic moments

1.2.2 音畫同步方法 實驗采用觸發(fā)器同時記錄圖像和聲音信號，實現(xiàn)了音畫同步。通過分析高速攝像機(jī)記錄的圖像信息和水聽器采集的聲壓脈動信息，得到了圖3所示的聲壓時變曲線與氣泡形態(tài)同步對應(yīng)圖，根據(jù)氣泡脫離管口瞬間頸縮斷裂會產(chǎn)生較強(qiáng)聲壓脈沖這一現(xiàn)象[38]，驗證了本實驗中所采用觸發(fā)器的準(zhǔn)確性。圖3展示了噴管管口脫離氣泡形成前后的形態(tài)與輻射聲壓脈動隨時間變化的對應(yīng)關(guān)系，可以看出，氣泡自管口脫離瞬間發(fā)生了頸縮斷裂，氣泡形態(tài)為上部球形底部圓錐形結(jié)構(gòu)，氣泡頸縮斷裂瞬間引發(fā)聲壓脈沖；隨后，在表面張力作用下，氣泡有保持最小表面勢能的趨勢，圓錐形氣泡頸部迅速向氣泡底部收縮，氣泡底部變?yōu)榍蛐危瑲馀葜車后w侵入氣泡底部，引發(fā)了氣泡體積振動，并產(chǎn)生強(qiáng)烈的聲壓信號，氣泡形態(tài)逐漸由球形變?yōu)槊毙巍４撕?，氣泡上升過程會發(fā)生高階形變，流場內(nèi)的聲壓脈動逐漸衰減，不再出現(xiàn)明顯的信號脈沖峰值，直至下一個氣泡在管口脫離。

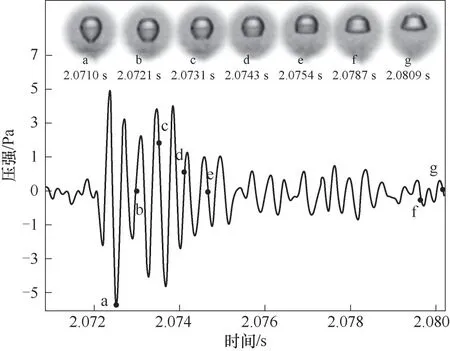
圖3 聲壓時域脈動波形與管口脫離氣泡形態(tài)同步對應(yīng)圖Fig.3 The time domain pulsation waveform of sound pressure corresponds synchronously to the shape of the bubble leaving the nozzle

2 實驗結(jié)果與討論

2.1 雙懸停氣泡破裂實驗觀測與分析

2.1.1 氣泡上升與懸停 根據(jù)氣泡與自由液面作用的行為差異，可將氣泡破裂過程分為兩類[39]，一類是氣泡升至自由液面反彈-懸停，進(jìn)而破裂；另一類是氣泡升至自由液面直接破裂。本文研究過程為第一類，在重復(fù)實驗的基礎(chǔ)上選取一組數(shù)據(jù)進(jìn)行詳細(xì)分析。

通過高速攝像機(jī)截取雙氣泡懸停-破裂幀圖像。雙懸停氣泡為非球體氣泡，本實驗中雙懸停氣泡與自由液面接觸長度、氣泡底部距自由液面的距離分別為5、4.68 mm和2.42、2.23 mm，兩氣泡間的初始距離為9.19 mm，如圖4所示。氣泡Ⅰ自噴管脫離，以無規(guī)則的高階形變不斷接近自由液面，與自由液面發(fā)生碰撞，具體表現(xiàn)為氣泡推動液面薄膜上凸后迅速回彈，氣泡薄膜在液面下部不斷震顫后趨于穩(wěn)定，最終懸停于自由液面底部，如圖4(a)所示。氣泡Ⅱ以相同方式上升并懸停于液面底部。經(jīng)結(jié)果統(tǒng)計，氣泡Ⅰ、氣泡Ⅱ脫離噴管兩時刻相差0.318 s。氣泡Ⅰ、氣泡Ⅱ懸停時間分別為0.4411、0.1555 s。值得注意的是，氣泡Ⅱ液面上凸與氣泡薄膜震顫程度更為劇烈，且懸停時間遠(yuǎn)小于氣泡Ⅰ，葉曦等[40]從入射沖擊波強(qiáng)度角度對氣泡向上拱出液面的運動程度不同作了解釋。

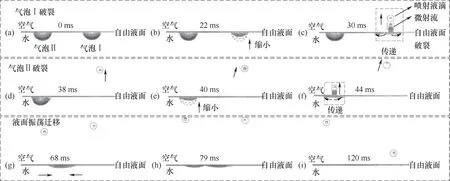
圖4 雙懸停氣泡破裂過程Fig.4 Double hovering bubble burst process

2.1.2 雙懸停氣泡破裂與液面振蕩波疊加 氣泡Ⅰ、氣泡Ⅱ相繼破裂。根據(jù)Israelachvili理論，當(dāng)氣泡液膜逐漸減薄至臨界厚度時，熱波動或Londonvan der Waals力在液膜變薄過程中起主要作用。懸停氣泡液膜破裂瞬間，系統(tǒng)總勢能突變，致使空腔凹陷底部產(chǎn)生諸多不同毛細(xì)波。根據(jù)質(zhì)量守恒和動量守恒，毛細(xì)波向腔體中心聚焦，產(chǎn)生了明顯的渦流。圖4(b)中具體表現(xiàn)為氣泡的急劇收縮。毛細(xì)波聚集到空腔中心，聚焦毛細(xì)波產(chǎn)生的空腔自相似坍塌導(dǎo)致了高速射流從液面噴射[14]，如圖4(c)所示。由于毫米量級氣泡不產(chǎn)生膜液滴，且懸停氣泡破裂過程不存在液帽[41]，射流產(chǎn)生后，在表面張力作用下，射流終端破碎分離成噴射液滴，射流其余部分在重力和黏滯力的作用下落回液面[18]，如圖4(d)所示。聚焦過程中，不同毛細(xì)波在不同的時間到達(dá)腔體中心，導(dǎo)致腔體底部在射流形成和噴射前快速振蕩[17]。雙懸停氣泡相繼破裂引起的液面振蕩波遷移，在靠近氣泡Ⅱ處存在明顯的波動疊加現(xiàn)象，液面波動瞬時疊加后仍沿原方向繼續(xù)傳播，直至波動消失，如圖4(f)~(i)所示。

2.2 雙懸停氣泡破裂聲疊加分析

氣泡的動態(tài)演化過程伴隨有特殊的聲壓信號產(chǎn)生，為了分析兩個懸停氣泡破裂聲特性及其影響，聲特性分析區(qū)間如圖5所示，選取氣泡Ⅱ自噴管脫離至雙懸停氣泡破裂過程。圖5(Ⅰ)為氣泡Ⅱ脫離管口聲壓時變曲線，作為參考區(qū)間；圖5(Ⅱ)為氣泡Ⅰ破裂聲壓時變曲線；圖5(Ⅲ)為氣泡Ⅱ破裂聲壓時變曲線；圖5(Ⅳ)為液面振蕩波疊加聲壓時變曲線。圖中點a~e為聲壓脈動峰值特征點。

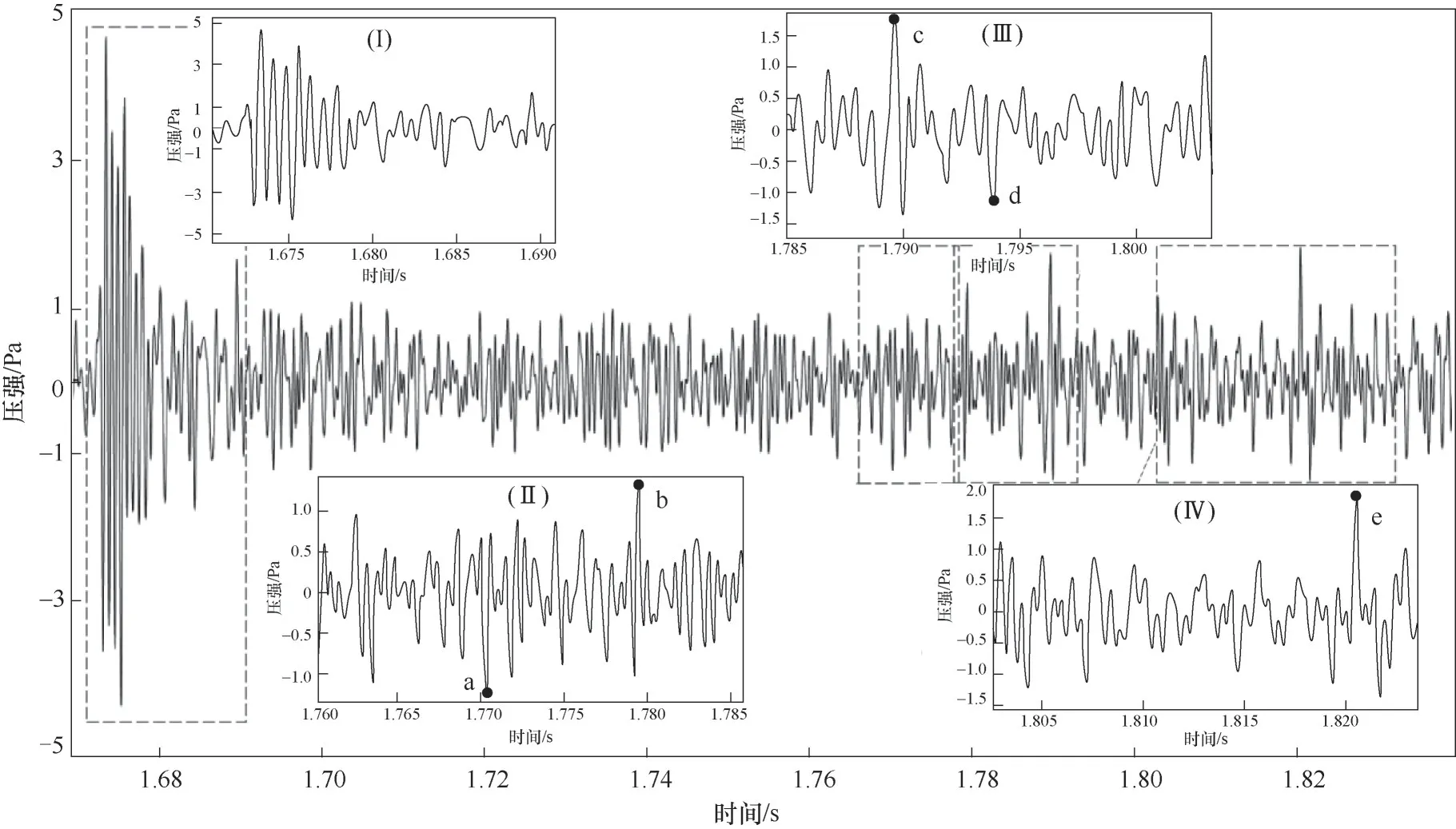
圖5 氣泡生成與破裂過程聲壓時域脈動波形圖Fig.5 Time-domain pulsation waveform of sound pressure during bubble formation and rupture

2.2.1 基于氣泡破裂重疊現(xiàn)象的聲特性 圖6對比分析了氣泡形態(tài)與聲壓的對應(yīng)關(guān)系，可以看出，1.7699 s氣泡Ⅰ因毛細(xì)波聚焦劇烈收縮，聲壓脈動峰值迅速激增至1.22 Pa。此后，聲壓脈動曲線在1 Pa范圍內(nèi)上下波動，直至1.7795 s凹陷腔體液面振蕩和射流產(chǎn)生時，聲壓脈動峰值迅速提升至1.34 Pa。在氣泡Ⅰ射流形成過程中，1.7897 s氣泡Ⅱ體積急劇收縮，此時引發(fā)了1.74 Pa的聲壓脈沖峰值，氣泡Ⅱ破裂產(chǎn)生的射流于1.7938 s形成，聲壓脈動幅值為1.14 Pa。雙懸停氣泡相繼破裂時間間隔極短，使得雙懸停氣泡破裂過程出現(xiàn)重疊，相較單個氣泡收縮和破裂形成射流過程，在聲壓上體現(xiàn)為聲壓脈沖峰值瞬時小幅激增。對單個氣泡破裂過程進(jìn)行反復(fù)實驗，聲壓峰值均分布于1.3 Pa附近。極短時間內(nèi)雙懸停氣泡相繼破裂過程中，1.7897 s存在聲壓幅值激增現(xiàn)象，聲壓幅值高于單氣泡破裂聲壓幅值約0.5 Pa，且該時刻恰好處于氣泡Ⅰ射流形成和氣泡Ⅱ體積急劇收縮的重疊部分。鑒于單氣泡液面破裂體積急劇收縮與射流產(chǎn)生均會引起聲壓幅值小幅提升，但均小于1.7897 s時刻的聲壓幅值，故聲壓在該時刻出現(xiàn)了瞬時疊加；但此聲壓幅值遠(yuǎn)小于氣泡脫離噴管管口瞬間的聲壓幅值。此外，氣泡高階形變引發(fā)的聲壓幅值變化，較氣泡破裂的聲壓幅值低4~5 Pa。

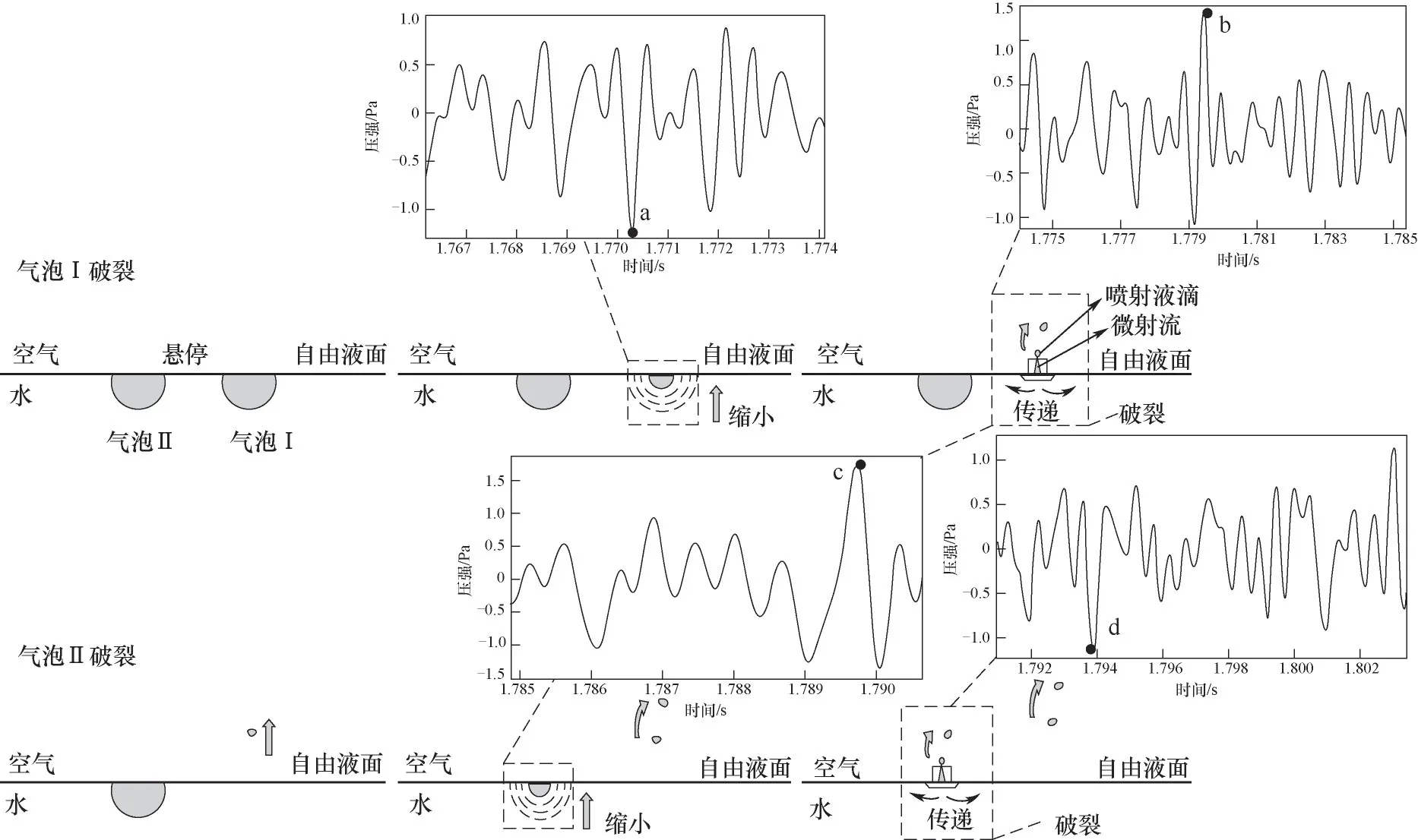
圖6 雙懸停氣泡破裂過程氣泡形態(tài)與聲壓變化示意圖Fig.6 Schematic diagram of bubble shape and sound pressure change in the process of double hovering bubble rupture

圖7(a)為1.6750、1.7699、1.7795、1.7897、1.7938 s五個時刻的聲信號時-頻曲線，分別對應(yīng)氣泡Ⅱ噴管管口脫離生成時刻、a~d點聲壓突變特征點對應(yīng)時刻。圖7(b)為a~d點聲壓突變特征點對應(yīng)時刻的聲信號時-頻曲線。由圖可知，1.6750 s氣泡自噴管管口脫離生成時刻聲信號的中心頻率為1336 Hz；a~d點特征點聲信號中心頻率由高到低分別為b點1828 Hz、a點1406 Hz、d點1336 Hz、c點1078 Hz，氣泡Ⅰ射流形成和氣泡Ⅱ體積急劇收縮的重疊時刻聲信號中心頻率最小，均小于單氣泡急劇收縮、射流產(chǎn)生時刻聲信號的中心頻率。

圖7 氣泡上升與破裂特征時刻聲信號時-頻曲線Fig.7 Acoustic signal time-frequency curve of bubble rising and bursting characteristic moment

2.2.2 基于液面振蕩波疊加現(xiàn)象的聲特性 氣泡Ⅰ、Ⅱ相繼破裂引起了自由液面振蕩，產(chǎn)生了相向傳播的振蕩波，在靠近氣泡Ⅱ的位置處有明顯的波動疊加，如圖8所示。1.8205 s為雙懸停氣泡破裂引起的液面振蕩波疊加時刻，聲壓時變曲線出現(xiàn)峰值1.83 Pa，隨后液面波動沿原方向繼續(xù)傳播，直至消散。波動疊加前后聲壓峰值均在1 Pa附近變化，有且僅在液面振蕩波疊加時刻，激增約至疊加前聲壓幅值的兩倍，在隨后的較長時間內(nèi)聲壓幅值不再增加。因此，雙懸停氣泡破裂導(dǎo)致的液面振蕩波疊加亦引起了聲壓的瞬時疊加。

圖8 雙懸停氣泡破裂過程氣泡形態(tài)與聲壓變化示意圖Fig.8 Schematic diagram of bubble shape and sound pressure change in the process of double hovering bubble rupture

圖9為1.7699、1.7795、1.7897、1.7938、1.8205 s五個時刻的聲信號時-頻曲線。1.8205 s對應(yīng)雙懸停氣泡破裂引起的液面振蕩波疊加e時刻，由圖可知，e時刻聲信號有兩個頻率峰值，中心頻率分別為e1點1242 Hz和e2點2063 Hz，雙中心頻率現(xiàn)象在重復(fù)實驗中得以驗證。

圖9 氣泡破裂過程特征時刻聲信號時-頻曲線Fig.9 Acoustic signal time-frequency curve of bubble bursting process characteristic moment

3 結(jié) 論

（1）雙懸停氣泡在自由液面處破裂時會產(chǎn)生次級聲壓，該聲壓小于氣泡脫離管口瞬間產(chǎn)生的聲壓，大于氣泡上升過程高階形變振動引起的聲壓脈動，前兩者差值約為4~5 Pa。

（2）雙懸停氣泡幾近同時破裂過程出現(xiàn)重疊，重疊時刻聲壓幅值較單氣泡破裂高約0.5 Pa，具體表現(xiàn)為聲壓脈沖峰值瞬時小幅激增。通過分析論證，明確了懸停氣泡急劇收縮與射流形成過程重疊導(dǎo)致了聲壓的小幅疊加。

（3）雙懸停氣泡破裂引起的液面振蕩波疊加過程中，有且僅在液面波動疊加時刻，聲壓峰值激增約至疊加前聲壓幅值的兩倍。故雙懸停氣泡破裂導(dǎo)致的液面振蕩波疊加引起了聲壓的瞬時疊加。

（4）基于雙懸停氣泡破裂重疊現(xiàn)象的聲信號僅有一個中心頻率，而基于雙懸停氣泡破裂引起的液面振蕩波疊加現(xiàn)象的聲信號具有兩個幅值相近、數(shù)值不同的中心頻率。