高校突發事件演變機理與應急管理評價
李玉飛, 劉曉云, 劉 洋
(武漢科技大學a.機械自動化學院,b.資源與環境工程學院,武漢 430081)
0 引 言
近年來,我國高校突發事件數量不斷增加。高校突發事件具有突發性、擴散性等特點[1-3],容易對高校和社會造成不良影響,已成為影響高校穩定和發展的重要因素[4-5]。弄清高校突發事件的產生原因、發生條件、演變規律是有效管控高校突發事件的前提和基礎,以便為高校管理者科學決策提供參考依據。因此,開展高校突發事件演變機理研究顯得尤為重要。
目前,一些專家學者對高校突發事件開展了較多研究。劉效廣等[6]采用心理試驗,選取高校大學生作為研究對象,探討了突發事件應急決策中的首因效應,分析了決策者情緒和后果嚴重性對首因效應的影響;張義庭等[7]基于熵理論,構建了高校突發事件網絡輿情模型,闡釋了高校網絡輿情系統內部的相互作用及影響;呂美等[8]從高校突發事件預警角度出發,構建了高校突發事件預警信息分析模型;皮祖訓等[9]基于灰色關聯理論,建立了校園安全灰色關聯評價模型;張欣[10]結合問卷調查和離散選擇模型,分析大學生在校園突發事件中的信息傳播行為偏好;楊霞等[11]采用層次分析和專家評分法,構建了高校突發事件應急管理能力的模糊綜合評價模型;周榮喜等[12]基于Delphi-AHP和加權集值統計,提出了高校突發事件預警評估方法。
以上專家學者從高校突發事件應急決策、網絡輿情管理、預測預警、評價模型構建等不同維度開展了研究,取得了較多研究成果,對高校突發事件應急管理具有重要的指導意義。從非線性數學角度來看,高校突發事件是偏離平衡狀態的非線性突變過程,突發性是高校突發事件的主要特征。在高校突發事件應急管理研究中,學者大多將高校突發事件分為事前、事中和事后3 個階段,但未從高校突發事件本身的非線性、突變性等內在屬性出發闡述其階段劃分依據,缺乏一定的理論基礎,導致所采取的應急管理方案實效性不強,需要進一步弄清高校突發事件的演變過程,進而提出有針對性的應急管理對策。
突變理論是研究不連續現象的新興科學,根據突變模型的勢函數,可分析臨界點附近非連續狀態的特征,展現系統在連續性的變化中突然中斷,引起質變的過程,進而分析出現的突變現象。目前,突變理論已應用到危化品道路運輸系統安全評價[13]、長三角生態安全評價與預警[14]、害蟲種群動態模型[15]、風電場群靜態電壓穩定性分析[16],涉及社會科學、生物科學、物理科學等諸多領域,以上應用證明了突變理論具有較好的適用性。基于此,采用突變理論,分析高校突發事件的突變特征,闡釋高校突發事件的非線性演變機理。在突變理論的基礎上,構建高校突發事件應急管理評價的突變級數模型,并結合實例進行說明。
1 高校突發事件的突變特征
當研究對象的系統參數變化時,突變模型勢函數描述的系統具有多平衡位置、跳躍性、滯后性、不可達性等突變指征,可以解釋系統中出現的不連續狀態。高校突發事件具有明顯的突變特征[17-18],因此可以采用突變模型分析高校突發事件的突變特征。
在初等突變模型中,尖點突變模型臨界曲面容易構造,且幾何直觀性強,應用最為廣泛,因此選用尖點突變模型。尖點突變模型的平衡曲面如圖1 所示。
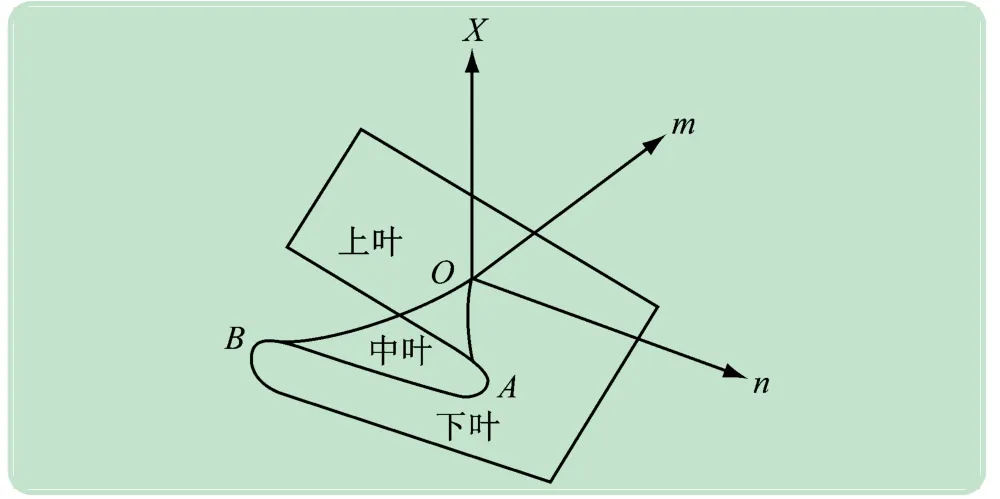
圖1 尖點突變模型的平衡曲面
(1)多平衡位置。從圖1 中知,位于中葉的勢函數取極大值,系統的平衡位置具有不穩定性,位于上葉和下葉的平衡位置是穩定的。當高校發生突發事件時,系統處于不穩定狀態;未發生突發事件時,系統將保持穩定平衡狀態,此時系統勢函數對于控制參數的某些范圍內可能有2 個或多于2 個的極小值。
(2)跳躍性。外界條件發生變化時,將導致系統狀態發生變化。在圖1 中,當系統的平衡位置在上葉時,在外在因素的影響下,平衡位置將突躍到下葉。高校內某一外部因素的變化可能導致突變事件的突然發生,系統狀態將由原來的穩定平衡狀態轉向不穩定狀態,即發生突發事件。
(3)滯后性。當物理過程并非嚴格可逆時,會出現滯后性,而突變過程具有不可逆的特征。高校突發事件的發生具有突發性,高校管理者在人員傷亡、影響范圍等方面的信息獲取需要一定的時間,使得在判斷決策上出現一定的滯后性,需要建立和完善高校應急管理快速反應機制。
(4)不可達性。圖1 中由不穩定穩態點組成的區域穿插在定態穩定點之間,這些點是不能實現的定態點。高校突發事件的發生受內部、外部等多種因素的影響,只有達到突發事件的條件時,才會發生突發事件。因此,在高校突發事件應急管理中,要重視加強突發事件影響因素管控,查漏補缺。
2 高校突發事件的演變機理
2.1 雙尖點突變模型
由突變理論知,雙尖點突變模型可以解釋非線性系統失穩的突變過程,為此將高校視為一個整體系統,建立系統動力學方程和勢函數,構建高校突發事件的雙尖點突變模型,闡釋高校突發事件的動態演變機理,分析高校從安全狀態演變為突發事件狀態的過程。
雙尖點突變模型的標準平衡曲面方程為:
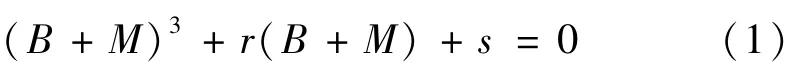
式中,r、s為控制變量,B +M 為狀態變量,可將狀態變量看作由B 和M兩個變量組成,式(1)可視為由兩個尖點突變模型構成的雙尖點突變模型,如圖2 所示。
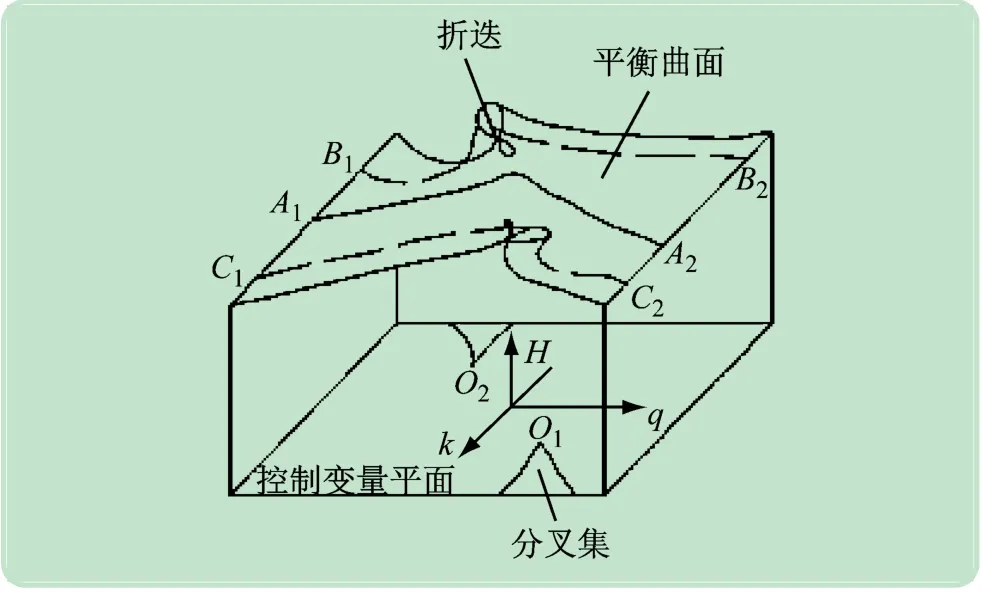
圖2 雙尖點突變模型
2.2 非線性演變機理
將圖2 中兩個位于分叉集尖角處的尖點位置坐標分別設為O1(f1,k1)和O2(f2,k2)。k 值的不同對高校是否發生突發事件具有不同的響應,這里可以把f 值看作系統發生突發事件的內在因素,把k 值看作外界條件的集合,將k值分為k2<k <k1、0 <k <k2、k >k13種情形,系統在控制變量平面上的投影如圖3-5 所示,分別與圖2 中A1A2、B1B2、C1C2曲線對應。
當k2<k <k1時,從圖3 可以看出,系統隨著f 值的變化而連續變化,系統呈現近乎線性的趨勢,此時系統不會發生失穩,即高校不發生突發事件。
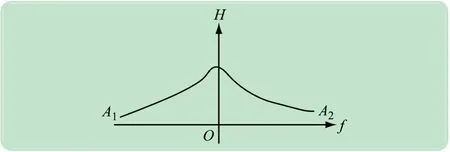
圖3 k2 <k <k1 時在控制變量平面上的投影圖
當0 <k <k2時,在圖4 中,從左向右分析f 值時,可將系統失穩過程分為曲線B1a1階段、a1b1階段和b2B2階段,進而分析高校突發事件的演變機理。在曲線B1a1階段,系統出現連續變化,此時高校不會發生突發事件;在曲線a1b1階段,當f 值增大到某一量值,系統發生突躍,高校從安全狀態演化為突發事件狀態,該階段驗證了高校突發事件是一種非線性的突變過程;在曲線b2B2階段,f值繼續增大,系統呈線性變化,表明高校突發事件已經結束,高校重新恢復到穩定狀態。當從右向左分析f 值時,分析過程與從左向右分析f值相同。由此可知f值不同,導致高校突發事件的演變路徑也不同。
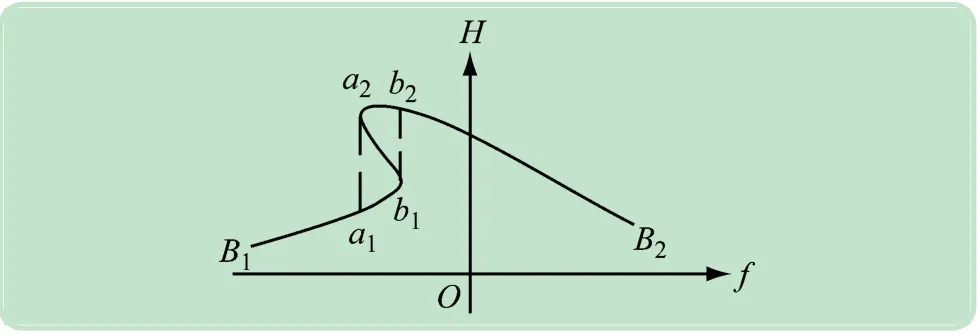
圖4 0 <k <k2 時在控制變量平面上的投影圖
當k >k1時,從圖5 可以看出,系統發生突發事件的演化規律與0 <k <k2時類似,不同的是系統發生突躍的f值不同。

圖5 k1 <k時在控制變量平面上的投影圖
從以上分析可知,影響高校突發事件的生成因素既包括外界條件的集合k值,也包括內在因素f值,內外因素構成了高校突發事件的充要條件。其中,內在因素f值是高校發生突發事件的根本原因,也是高校發生突發事件的必要條件。
2.3 演化階段
基于突變理論,采用雙尖點突變模型可以闡釋高校突發事件非線性系統的失穩過程,證明了突變理論適用于高校突發事件演變機理研究。結合圖4,可將系統非線性失穩過程的曲線B1a1階段、a1b1階段和b2B2階段分別定義為穩定量變階段、失穩質變階段和穩定恢復階段。
在穩定量變階段,該階段可以看作是高校突發事件的前兆。本階段若不采取措施,在各種風險的累積疊加效應作用下,高校內部的能量將不斷集聚,當總能量積累到一定程度時,會造成平衡狀態的勢函數發生突變,導致高校發生突發事件。為避免系統從穩定量變階段轉向失穩質變階段,可對影響系統的外部和內部因素施加作用,阻斷內因和外因同時發生作用,防止兩者形成合力,阻止或延緩能量的聚集過程。
在失穩質變階段,該階段可以看作是高校突發事件的發生過程。為高校減輕突發事件發生的烈度,使損失最小化,應實施應急預案,重點布防,防止事態擴大化;或人為改變系統突變發生的路徑,使突變向相對有利的方向發生;或改變造成系統發生突變的內在和外部因素,降低突變過程中的能量強度。由于失穩質變階段發生時間較短,為高校管理者預留出有效控制的時間有限。因此,在實際情況中,高校要針對不同類型的突發事件加強研判和分析,制定不同的應急預案,定期開展應急演練。
在穩定恢復階段,該階段可以看作是高校突發事件的事后管理過程。高校突發事件結束后,系統內部的能量逐步釋放,高校恢復到原有的穩定狀態。在這一階段,高校要做好善后處置工作,減輕突發事件造成的損失與影響。同時,高校要對突發事件開展調查分析,完善和優化應急處理措施和應急方案,提高高校應對突發事件的應急儲備。
3 高校突發事件的應急管理評價
3.1 應急管理評價指標體系
影響高校突發事件應急管理評價的因素較多,以往高校突發事件應急管理評價指標體系的構建主要基于突發事件的階段性,側重于各個階段的管理。而由高校突發事件演變機理知,高校突發事件的影響因素包括外界條件和內在因素,內在因素是高校突發事件的發生根源,高校突發事件應急管理評價應重點強調內外因素的共同作用。因此,從制度管理、物質保障、精神保障、安全教育、事后改進等方面選取評價指標。在前人研究成果的基礎上[19],遵循評價指標選取的全面性、代表性等原則,選取安全管理規章制度預案、安保人員應急救援等12 個評價指標,并根據評價指標的重要性排序結果,建立高校突發事件應急管理評價指標體系,如表1 所示。

表1 高校突發事件應急管理評價指標體系
參考高校突發事件應急管理分級標準,結合突變級數法計算結果特性,將高校突發事件應急管理等級劃分Ⅰ(優)、Ⅱ(良)、Ⅲ(中)、Ⅳ(一般)、Ⅴ(差)共5個等級,Ⅰ級表示達到評價標準的95% ~100%為優,Ⅱ級表示達到評價標準的85% ~95%為良,Ⅲ級表示達到評價標準的75% ~85%為中,Ⅳ級表示達到評價標準的60% ~75%為一般,Ⅴ級表示達到評價標準的0% ~60%為差,高校突發事件應急管理分級劃分標準如表2 所示。
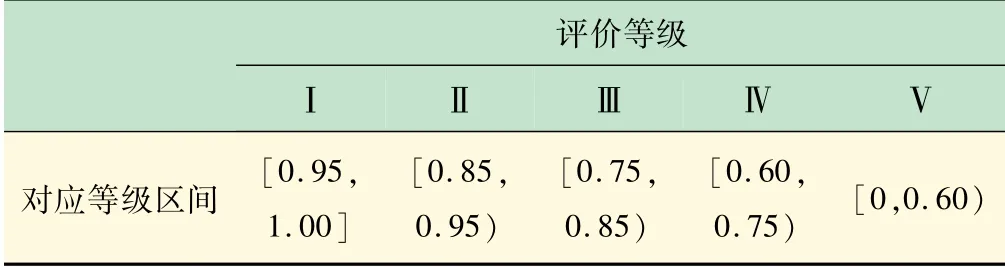
表2 高校突發事件應急管理等級劃分標準
3.2 應急管理評價的突變級數模型
突變級數法是突變理論和模糊數學理論相結合的一種評價方法,通過歸一化公式,得到各層的突變隸屬函數值,進而獲得研究對象的突變級數值,實現對評價指標體系的量化分析。根據表3 的突變模型類型和表1 的高校突發事件應急管理評價指標體系,構建高校突發事件應急管理評價的突變級數模型,如圖6 所示。

表3 突變模型的常見類型
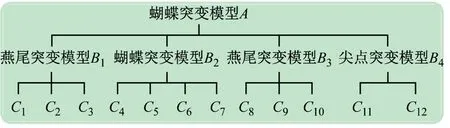
圖6 高校突發事件應急管理評價的突變級數模型
3.3 應急管理分析
由于評價指標為定性指標,較難直接獲取,故采取專家打分法確定。選取某一高校,聘請5 位高校突發事件相關研究領域的專家,結合高校實際情況和表2的高校突發事件應急管理等級劃分標準與要求,對高校進行打分,專家打分結果如表4 所示。
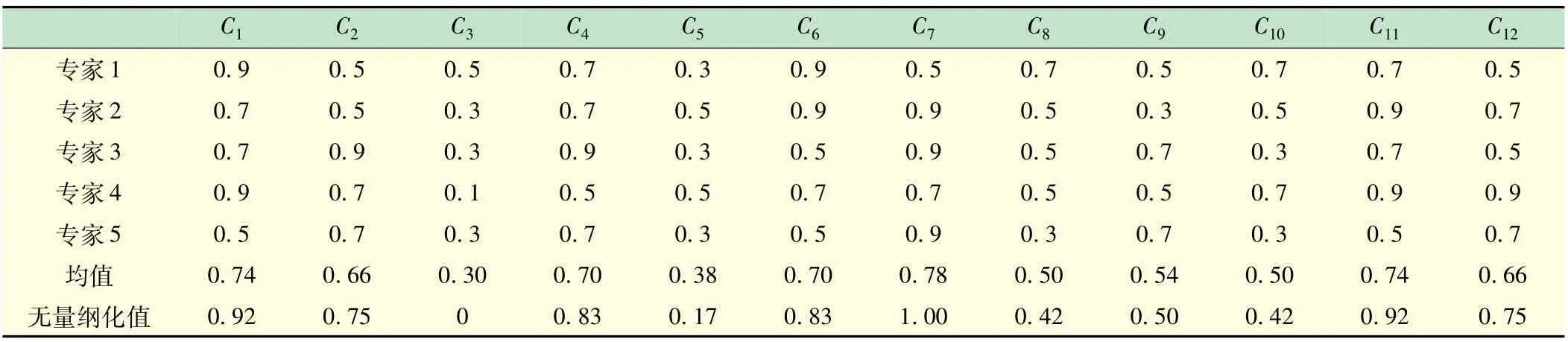
表4 專家打分結果
根據圖6 的高校突發事件應急管理評價的突變級數模型,利用表3 的歸一化公式,由無量綱化處理的標準化數據,逐層向上計算各層控制變量的值,即突變隸屬函數值,最終計算出A層的突變級數值。計算過程如下:
B1與C1、C2、C3構成燕尾突變模型,則XC1=(0.92)1/2=0.949,XC2=(0.75)1/3=0.909,XC3=0。由于控制變量間具有相關性,按照“互補”原則,取平均值,則B1=average{0.949,0.909,0}=0.619。
B2與C4、C5、C6、C7構成蝴蝶突變模型,則XC4=(0.83)1/2=0.911,XC5=(0.17)1/3=0.554,XC6=(0.83)1/4=0.954,XC7=1.000。由于控制變量間無相關性,按照“非互補”原則,大中取小,則
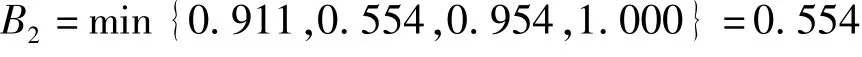
B3與C8、C9、C10構成燕尾突變模型,則XC8=(0.42)1/2=0.648,XC9=(0.50)1/3=0.794,XC10=(0.42)1/4=0.805。按照“互補”原則,則
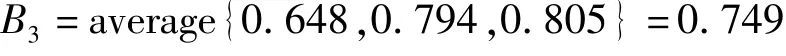
B4與C11、C12構成尖點突變模型,則XC11=(0.92)1/2=0.959,XC12=(0.75)1/3=0.909。按照“非互補”原則,則B4=min{0.959,0.909}=0.909。
A1與B1、B2、B3、B4構成蝴蝶突變模型,則XB1=(0.619)1/2=0.787,XB2=(0.554)1/3=0.821,XB3=(0.749)1/4=0.930,XB4=(0.909)1/5=0.984。按照“非互補”原則,則
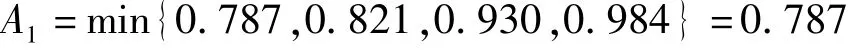
最終計算得到的A 層突變級數值為0.787,根據表2 的高校突發事件應急管理等級劃分標準,確定該高校的等級為Ⅲ,這與專家實際調研結果基本一致,驗證了將突變級數模型應用于高校突發事件應急管理評價是可行的。
在同一層突變模型中,可計算該層某一評價指標的突變隸屬函數值占同層突變模型總突變隸屬函數值的比值,比重越大,說明該評價指標的能力越好。相反,比重越小,說明該評價指標的能力越差,需要對能力差的評價指標進行重點管理,進而有效預防高校突發事件的發生。
以蝴蝶突變模型B2和A 為例,由圖7 可見,校園精神保障C5在蝴蝶突變模型B2中突變隸屬函數值占比最低為16.2%,說明評價指標校園精神保障C5較差,應加校園精神保障能力建設。同理,對于蝴蝶突變模型A而言,應加強安全保障能力建設。
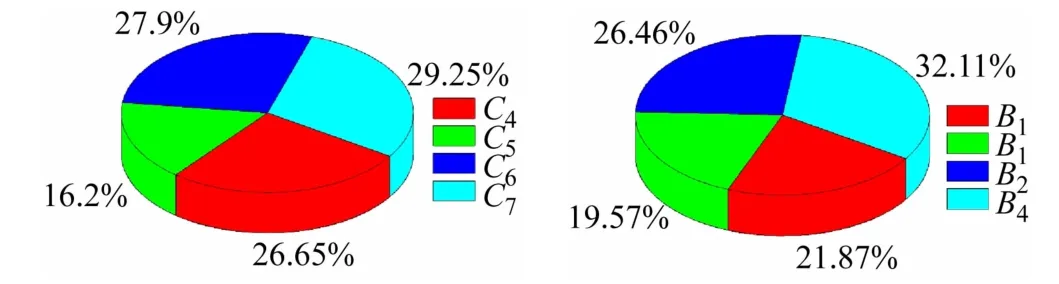
圖7 樣本中評價指標的突變隸屬函數值占比
4 結 語
(1)從非線性的角度出發,采用突變理論分析了高校突發事件的多平衡位置、跳躍性、滯后性、不可達性等特征,這與突變模型勢函數描述的突變指征一致,表明利用突變理論分析高校突發事件突變特征具有較好的適用性。
(2)選用雙尖點突變模型,采用定性的數學描述,闡釋高校突發事件的非線性演化機理,分析高校從安全狀態演化為突發事件狀態的失穩過程,驗證了高校突發事件是一種偏離平衡狀態的非線性突變過程,并將高校突發事件非線性失穩過程分為穩定量變階段、失穩質變階段和穩定恢復階段。
(3)將突變理論和模糊數學理論相結合,形成突變級數法,構建了高校突發事件應急管理評價的突變級數模型。通過計算評價指標的突變隸屬函數值占同層突變模型的總突變隸屬函數值的比值,判斷和識別出有待加強的評價指標,為高校突發事件應急管理提供決策依據。
(4)本文著重從理論角度探討了高校突發事件的非線性演變機理,將高校突發事件的演化過程劃分為3 個階段。下一步,將研究如何在高校突發事件不同階段中加強外部因素和內在因素管理,提供切實可行的應對方案。同時,將擴充檢驗樣本的數量,對構建的高校突發事件應急管理評價的突變級數模型作進一步驗證。
·名人名言·
人不光是靠他生來就擁有一切,而是靠他從學習中所得到的一切來造就自己。
——歌德

