通信系統解調損失測試方法研究

余清華，叢 波，邱 斌，孫 建，王志虎，丁風海

(中國衛星海上測控部, 江蘇 江陰 214431)

1 引 言

在無線電測控領域，解調損失是評價測控設備解調性能的關鍵參數，比如誤比特率、遙測解調門限等都直接與解調損失相關聯，對解調損失測試的準確度直接影響誤比特率、遙測解調門限的計算精度，因此解調損失的測試非常關鍵。然而目前并無解調損失測試的相關標準，特別在引用理論誤碼率公式以及保證置信度情況下的碼元測試長度的標準不一。針對此情況，本文擬基于解調損失測試原理，對部分容易引用錯誤的調制體制的理論誤碼率以及長期引用錯誤的調制體制的理論誤碼率進行分析，并推導誤碼率在特定置信度條件的測試長度，從而進一步規范解調損失的測試。

2 解調損失的測試原理

影響解調損失的因素有很多，最主要的有：射頻器件的非線性與噪聲、傳輸通道的干擾與衰落、濾波器的不匹配等。實際上，不論上述因素如何影響解調損失，最終都表現為誤碼率的變化，因此，解調損失與誤碼率之間存在著必然的聯系[1,2]。

數字基帶設備對應誤碼率Pe下的解調門限可以表示為：

(1)

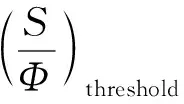
(2)

式中：erfc()函數為高斯誤差函數。

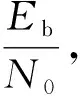
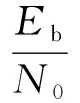
(3)

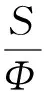
(4)

將式(4)代入式(1)中，得到：

(5)

由于比特速率相同，因此進一步化簡得到：

(6)

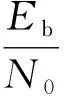
3 BPSK與CPFSK的理論誤碼率

3.1 BPSK的理論誤碼率

PSK信號解調采用乘法器加低通濾波器與乘法器加匹配濾波器的理論誤碼率的表達式會稍微不同，需要根據實際情況選擇理論誤碼率的表達式，然后再反向計算Eb/N0。BPSK相干解調的原理框圖如圖1所示。

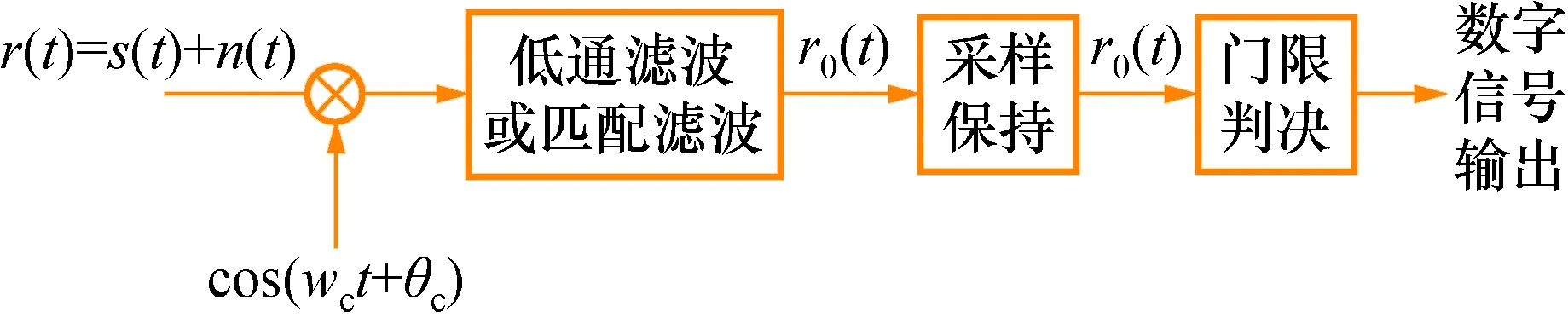
圖1 BPSK相干解調的原理框圖Fig.1 Principle block diagram of BPSK coherent demodulation

3.1.1 匹配濾波下的理論誤碼率

高斯白噪聲環境下，二進制信號在最佳判決門限設置下的理論誤碼率可以表示為[3]：

(7)

式中：s01、s02分別表示傳輸二進制1和傳輸二進制0的信號。

根據匹配濾波的性質[4]，在判決時刻t0，輸出信號的信噪比將達到最大值，輸出信號的信噪比可表示為：

(8)

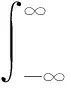
從式(8)可以看出，經匹配濾波器輸出的信噪比與信號的能量和噪聲的譜密度無關。

當信號sd=(s1-s2)經匹配濾波后，在判決時刻t0：

(9)

式中：

(10)

那么：

(11)

對于BPSK信號，假設：

(12)

那么采用匹配濾波，則：

(13)

將式(7)代入式(5)得到：

(14)

式中：Eb=A2T/2。

3.1.2 低通濾波下的理論誤碼率

對于式(6)的輸入信號，當使用低通濾波器(其帶寬B≥2/T)，其輸出可以表示為[5]：

(15)

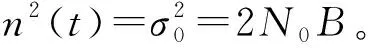
將式(9)代入式(1)中得到：

(16)

3.2 CPFSK的理論誤碼率

PCM/FM體制實際上就是含有預濾波的CPFSK(連續相位FSK)體制[6]，在一般工程應用中，PCM/FM (CPFSK) 大都采用基于鑒頻器的非相干解調方法。然而，關于這一方法的理論誤碼率至今尚無便于工程應用的解析公式。

目前，在遙測設備的研制和測試過程中，PCM/FM的理論誤碼率一般按照FSK非相干解調的理論誤碼率進行計算[7]，即:

規劃水資源論證工作是近年才啟動的新工作，目前還處于探索階段，本文結合湖南省長沙市大河西先導區規劃水資源論證工作，淺談論證的技術路線及遇到的幾個問題，并提出相應建議。

Pe=1/2·e-1/2·(Eb/N0)

(17)

然而，事實上，這個公式并不符合PCM/FM體制的情況。文獻[8]的分析也表明：上述公式和實際的理論誤碼率存在著顯著差異。

首先，這個公式只適用于FSK匹配濾波器方式的解調過程[9]。而PCM/FM體制基本均采用基于鑒頻器的解調方案。二者有一定區別。上述公式的根本問題是未能體現PCM/FM中調制頻偏的影響。PCM/FM中調制頻偏的影響。在FM體制中，調制頻偏越大，解調輸出的信噪比也就越高，而上述公式完全忽略了這一因素。其次，采用鑒頻器方案的PCM/FM解調的理論誤碼特性，在很大程度上依賴解調器的具體設計，如前置濾波器、中頻帶寬、檢后低通濾波器等等。而上述公式未能體現這些影響。另外，分析將表明，理論誤碼率將取決于遙測接收機中頻帶寬和檢后低通濾波器的相互關系[10]。

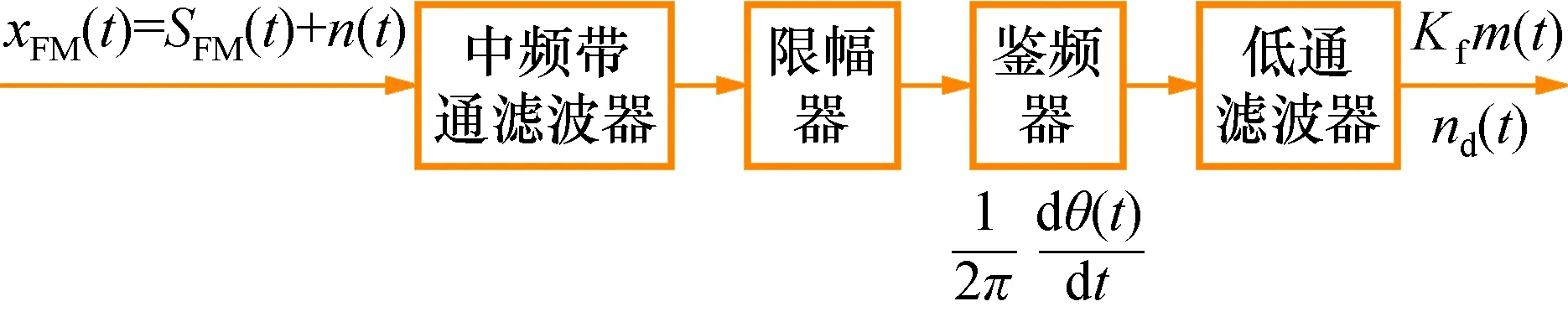
圖2 PCM/FM體制鑒頻解調原理示意圖Fig.2 Schematic diagram of PCM/FM system frequency discrimination demodulation

根據文獻[11]基于鑒頻器的PCM/FM解調誤碼率可表示為：

(18)

其中，當中頻帶寬小于或等于兩倍通濾波器帶寬時：

當中頻帶寬大于或等于兩倍低通濾波器帶寬時：

L=4/(3h2)

4 誤碼率測試的置信度分析

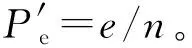
由概率論可知,統計置信度的計算依據是二項式分布函數[12,13],該函數的一般數學式為:

(19)

二次分布型事件只有2種可能的結果,因此p+q=1。對于誤碼率測試,主要了解n次試驗中事件發生的次數k≤N或k>N次的概率,N由誤碼率最低規范要求確定。因此,將式(19)對k進行累加,其結果為：

(20)

(21)

式(20)是誤碼發生k≤N次的概率，式(21)是誤碼發生k>N的概率。應用到數字通信系統中誤碼率測試時,根據定義,式(21)實際就是誤碼率優于某一規定標準的統計置信度,因此用累加二項式分布函數的方式,在誤碼率測試實驗中,統計置信度的數學式最終可表示為[14,15]：

CL=P[Pe≤Ph|e,n]

(22)

式中：Ph為數字通信系統或器件的誤碼率規定標準。式(22)為誤碼率測試置信度的原始定義。明顯利用利用原始定義直接計算會產生數據溢出從而導致計算結果不準確，因此需要進行簡化。對于式(20)，如果發送的比特數足夠多，使n×p>1，且k與n×p有相同的數量級，那么式(20)就可以用Poisson分布近似為[12,16～18]：

(23)

令k=e，p=Ph，則：

(24)

聯合求解n，可得：

(25)

從式(25)可以看出，在假設最大誤碼率水平，以及置信度的情況下，要不斷進行迭代計算。在迭代計算過程中涉及兩個問題，第一個迭代的步進，第二個是迭代收斂的判定條件。對于迭代的步進問題,如果選擇過小,如步進小于1/Ph，則會產生不是整數的錯誤碼元問題，顯然不符合實際情況，如果選擇過大則會導致收斂精度不夠，因此在這里選擇步進為1/Ph。對于迭代收斂條件判定問題，即判斷式(25)等號左右相差多少為收斂，收斂條件應該盡可能小但也不可能設置成無限制小，因為迭代步進限制了最小的收斂條件。經過反復計算實驗，當迭代步進為1/Ph時，最小收斂區間為0.03n。

在Matlab環境下進行計算，以系統誤碼率分別為10-4，迭代步進為104，計算置信度為99%需要測試的碼元數。這里需要指出的是，出現的錯誤碼元越少，得到99%的置信率，需要測試的碼元數就越短，為了保證解調損失的測試可靠，將出現的最大碼元數設置為測試的碼元總數乘以系統允許的最大誤碼率。運行matlab計算得到需要測試的碼元長度為136/Ph，即136/Pe。當測試的碼元數為136/Pe，允許的迭代收斂的誤差限為±4.08/Pe，那么收斂區間造成誤碼的平均個數為4.08個，由于錯誤碼元只能為整數，收斂區間造成誤碼的平均個數為5個，即允許的測試誤差為5/136×100%=3.6%。

5 實 驗

對BPSK和PCM-FM(CPFSK)兩種調制體制的數字通信設備的解調損失開展測試。測量連接框圖如圖3所示。

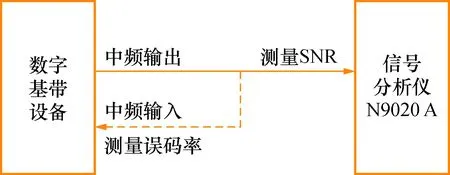
圖3 設備連接圖Fig.3 Device connection diagram

BPSK的碼率為64 kHz，碼型為NRZ-L碼，基帶的帶寬設置為150 kHz，碼元測試長度為1.36×106，測試結果如表1所示。

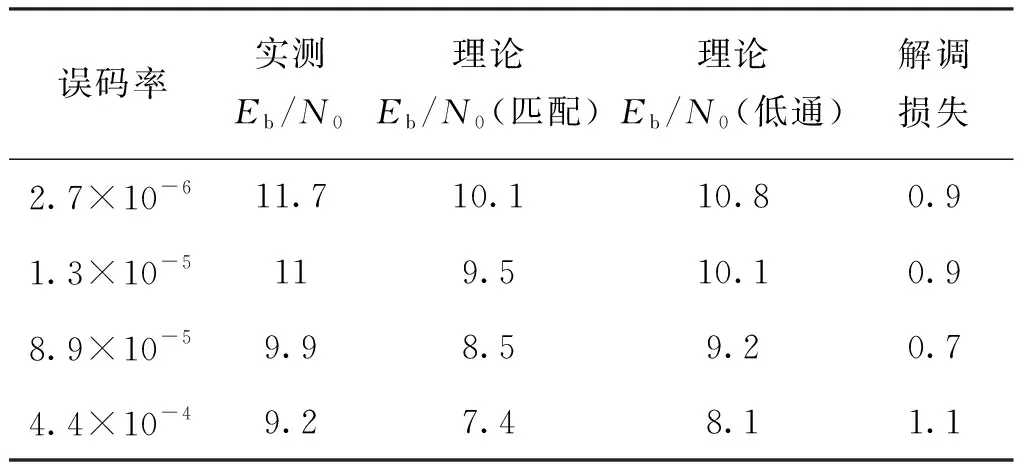
表1 BPSK的解調損失測試參數及結果表Tab.1 BPSK demodulation loss test parameters andresults table

由于使用低通濾波器引入的噪聲更多，如果此時直接應用教科書上的理論誤碼率的公式，則會引入約為0.7 dB的誤差。

PCM-FM(CPFSK)的碼率為1.966 08 MHz，碼型為NRZ-L碼，基帶的帶寬設置為3.3 MHz，碼元測試長度為136/Pe，測試結果如表2所示。

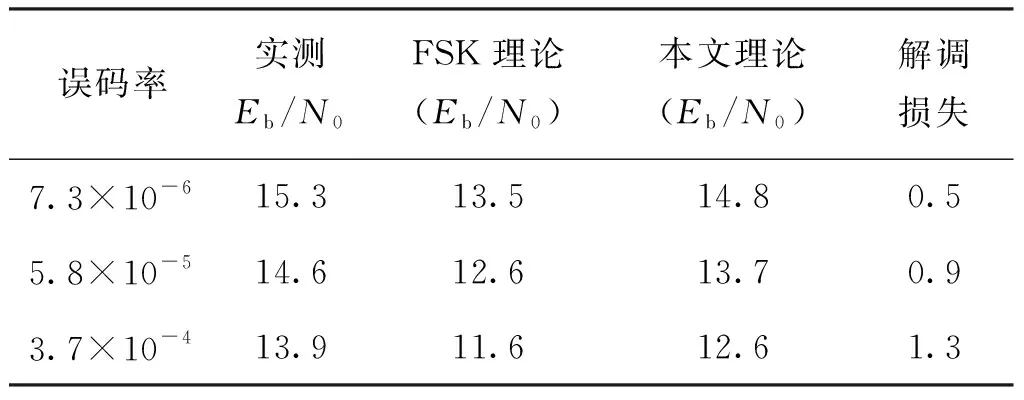
表2 PCM-FM的解調損失測試參數及結果表Tab.2 PCM-FM demodulation loss test parameters and results table dB

從表2中可以看出在相同誤碼率下，如引用FSK的理論誤碼率公式將造成超過1 dB誤差，而且從直接測試計算的結果看，本文引用的誤碼率公式更合理。

在PCM-FM調制體制下進行解調損失重復性測試，碼元測試長度分別為10/Pe和136/Pe。由于誤碼率的值無法控制，因此這里采用了將每次輸入的設置為相同(13.9 dB)，在10/Pe和136/Pe分別測6次，測試結果如表3所示。

表3 重復性測試結果Tab.3 results of repeatability dB

6 結 論

本文針對通信系統解調損失測試過程中存在的引用理論誤碼率不準確以及保證置信度情況下的碼元測試長度的標準不一的問題，對PSK以及CPFSK調制體制理論誤碼率進行了分析，對碼型對誤碼率的影響進行了梳理，推導了誤碼率測試置信度與測試碼元長度關系，給出了在0.99置信概率下的碼元測試長度(136/Pe)。開展了驗證實驗，實驗數據表明，錯誤的引用BPSK的理論誤碼率以及CPFSK將引起解調損失誤差分別不小于0.7 dB和1.0 dB(解調損失的指標一般不超過2.5 dB)；相對于136/Pe的碼元測試長度下的解調損失的重復性為0.08 dB，10/Pe的碼元測試長度下的解調損失的重復性增大了4倍。因此，為保證通信系統的解調損失的準確可靠，必須對相關的測試方法進行規范。