一類時空的分數(shù)階組合擴散方程的初邊值問題

管亭亭，張松濤

1.山西師范大學數(shù)學與計算機科學學院，山西 臨汾 041000；2.山西省臨汾工商行政管理學校，山西 臨汾 041000

0 引言

最值原理是研究擴散方程、復雜動力系統(tǒng)等現(xiàn)象的重要方法.通過最值原理，可以直接或間接獲得分數(shù)階偏微分方程解的一些重要性質(zhì)，如：解的唯一性、正解或負解的存在性、比較原理以及解的連續(xù)依賴性等.2009年，Luchko[1]給出了分數(shù)階偏微分方程最值原理的具體表達式.他應(yīng)用該原理獲得了一類廣義時間分數(shù)階擴散方程的解的存在性與唯一性[2,3].2016年，Jia和Li[4]研究了具有分數(shù)Laplace算子的時空分數(shù)階擴散方程.他們應(yīng)用時間分數(shù)階導數(shù)和分數(shù)Laplace算子的性質(zhì)，證明了古典解和弱解的最值原理.2019年，Wang[5]等研究了具有分數(shù)Laplace算子的Hadamard分數(shù)階偏微分方程的初邊值問題，得到并證明了該方程的最值原理，并應(yīng)用該原理得到了一些存在性與唯一性結(jié)果.2020年，Mokhtar和Berikbol[6]證明了分別具有時間分數(shù)階Caputo型導數(shù)和時間分數(shù)階Riemann-Liouville型導數(shù)的時空分數(shù)階擴散方程和時空分數(shù)階pseude-paraboic方程初邊值問題解的唯一性和連續(xù)依賴性.分數(shù)階微分方程的最值原理具有潛在的廣泛應(yīng)用，它引起了越來越多的學者的關(guān)注和研究[7～10].

Jarad[11]給出了Caputo型和Riemann-Liouville型分數(shù)階組合導數(shù)及它們的一些性質(zhì).據(jù)我們所知，關(guān)于Caputo型分數(shù)階組合導數(shù)的最值原理及其應(yīng)用的數(shù)學文獻還很少.受此啟發(fā)，本文研究了一類時空的Caputo型分數(shù)階組合擴散方程.首先，我們應(yīng)用Caputo型分數(shù)階組合導數(shù)的預備知識得到一個最值原理.其次，通過最值原理，我們得到了初邊值問題的解的估計、解的唯一性與連續(xù)依賴性.

本文結(jié)構(gòu)如下：第1部分給出一些關(guān)于Caputo型分數(shù)階組合導數(shù)的預備知識；第2部分證明最值原理；第3部分應(yīng)用最值原理獲得初邊值問題解的估計、解的唯一性與連續(xù)依賴性.

1 預備知識

本文我們研究一類時空的具有分數(shù)階組合導數(shù)的分數(shù)階擴散方程

(1)

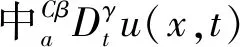
(2)

記

H={u(x,t)|u(x,t)∈C2,1((0,l)×(a,b]),u(x,t)∈C([0,l]×[a,b])}

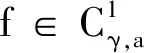
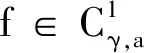
2 最值原理

在這一小節(jié)，我們考慮具有初邊值條件(3)的線性時空的具有Caputo型分數(shù)階組合導數(shù)的分數(shù)階擴散方程(1)，其中初邊值條件如下：

u(x,a)=φ(x)x∈(0,l)
u(0,t)=μ1(t)t∈[a,b]
u(l,t)=μ2(t)t∈[a,b]

(3)

定理1 假設(shè)u(x,t)∈H滿足具有初邊值條件(3)的線性時空Caputo型分數(shù)階組合擴散方程(1).當f(x,t)≤0，(x,t)∈(0,l)×(a,b]時，則

(4)

成立.

證明 以下用反證法證明定理成立.假設(shè)不等式(4)不成立，即存在一個點(x0,t0)∈(0,l)×(a,b]使得

(5)

記ε=u(x0,t0)-M，做函數(shù)

容易知W成立如下不等式

由W滿足的第二個不等式可知，W在[0,l]×{a}∪{0}×[a,b]∪{l}×[a,b]上取不到最大值.

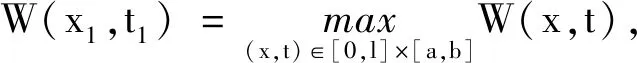
W(x1,t1)≥W(x0,t0)≥ε+M>ε

故在點(x1,t1)如下不等式成立

(6)

式(6)與式(1)矛盾，故假設(shè)不成立.證畢.

用-u代替u，同理可證下面這個定理.

定理2 假設(shè)u(x,t)∈H滿足具有初邊值條件(3)的線性時空Caputo型分數(shù)階組合擴散方程(1).當f(x,t)≥0，(x,t)∈(0,l)×(a,b]時，則

成立.

3 最值原理的應(yīng)用

定理3 假設(shè)u(x,t)∈H滿足具有初邊值條件(3)的線性時空Caputo型分數(shù)階組合擴散方程(1)，則

(7)

成立，其中M=‖f‖C([0,l]×[a,b]).

如果u(x,t)是滿足初邊值條件(3)的擴散方程(1)的解，則V(x,t)是擴散方程(1)的解其對應(yīng)的初邊值條件如下：

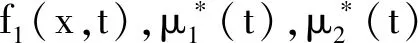
因此

(8)

同理可得

(9)

由式(8)及式(9)，定理得證.

定理4 假設(shè)u(x,t)∈H是具有初邊值條件(3)的擴散方程(1)的解.u(x,t)連續(xù)依賴于所給定的初始條件及邊界條件，即，如果

‖f1-f‖C([0,l]×[a,b])≤ε‖φ1-φ‖C([0,l])≤ε0

定理5 假設(shè)f(x,t)≤0,φ(x,t)≤0，μ1(x,t)≤0且μ2(x,t)≤0，如果u(x,t)∈H是具有初邊值條件(3)的擴散方程(1)的解，則

u(x,t)≤0 (x,t)∈[0,l]×[a,b]

成立.

定理6 假設(shè)f(x,t)≥0,φ(x,t)≥0,μ1(x,t)≥0且μ2(x,t)≥0，如果u(x,t)∈H是具有初邊值條件(3)的擴散方程(1)的解，則

u(x,t)≥0 (x,t)∈[0,l]×[a,b]

成立.

注1 假設(shè)f(x,t)=0,φ(x,t)=0,μ1(x,t)=0且μ2(x,t)=0，如果u(x,t)∈H是具有初邊值條件(3)的擴散方程(1)的解，則

u(x,t)=0 (x,t)∈[0,l]×[a,b]

成立.

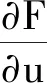
(10)

在H中如果有解必是唯一解.

證明 假設(shè)u1和u2是非線性初邊值問題(10)的兩個解.令

u(x,t)=u1(x,t)-u2(x,t) (x,t)∈[0,l]×[a,b]

則u滿足如下方程

(11)

由于

(12)

其中u*=(1-λ)u1+λu2,0<λ<1.

由式(11)及(12)可得

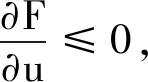
定理得證.