基于排隊論和邊際分析法的銀行服務窗口優化研究

裴秀艷，李波，

1.運城職業技術大學基礎課教學部，山西 運城 044000；2.建設銀行運城鹽湖支行，山西 運城 044000

0 引言

眾所周知，客戶在銀行排隊等候接受服務是一類常見的排隊現象.作為客戶來說，毫無疑問是想在盡可能短的時間享受最快捷、最完善的服務.而作為銀行服務來說要想縮短客戶的排隊等候時間，需要增加服務窗口，但這勢必會造成銀行運營成本的增加.如何尋求客戶需求與銀行服務滿意度二者之間的平衡，就需要優化銀行服務窗口的設置，使得合適的窗口數極大限度地滿足客戶的需求，提高客戶對銀行服務的滿意度，提升銀行的服務效率，從而增加銀行的市場競爭力.

1 排隊系統簡介

排隊模型在日常生活生產中有頗為廣泛的應用，如：顧客在超市排隊等候結賬；乘客在車站排隊購票；十字路口排隊等待信號燈的車輛；等待打印輸出的文件；撥打電話信號占線等排隊現象.上述排隊有的是看得見的有形排隊，有的是看不見的無形排隊[1].日常生活中的排隊現象通過建立數學模型，都可以轉化為排隊論的問題進行研究，尋求最佳的優化解決方案.

研究隨機服務系統工作過程的數學理論和方法稱為排隊論，又稱隨機服務系統，它是運籌學的一個重要分支.一般來說，排隊系統[2]由3個基本部分組成：

(1)到達規則：描述顧客到達系統的規律，是單個到達還是批量到達，到達時間間隔服從的時間分布.

(2)排隊規則:a.等待制：顧客到達系統時，若所有服務臺均繁忙，顧客需要排隊等待接受服務，即認定為等待制.等待接受服務的順序可以是誰先到達誰先服務，也可是后到先服務，或者是帶有優先權的服務(例如：醫院對危重癥患者優先治療)；b.損失制：顧客到達系統后，若所有服務臺均繁忙，則隨即離開系統；c.混合制：及上述兩種情況的綜合，如：可容納的等待空間有限，多余的顧客必須離開系統即損失制，其余的為等待制.

(3)服務規則:可以是單一服務臺，也可是多服務臺.多服務臺有并聯和串連兩種排列方式.接受服務的時間可服從隨機分布或者是確定時間分布(例如：自動洗車裝置的洗車時間).

排隊系統按照3個基本組成部分可以進行分類，通常用符號X/Y/Z來表示(圖1所示).X表示到達時間間隔服從的分布；Y表示服務時間服從的分布；Z表示服務臺個數，其中，用M表示到達時間間隔或者是服務時間服從負指數分布.

圖1 排隊論的基本結構Fig.1 Basic structure of queuing theory

2 銀行排隊模型的建立

在銀行排隊系統中，服務臺為銀行窗口柜臺，服務員為銀行柜員，等待接受服務的客戶稱為顧客，三者組成一個隨機服務系統，即銀行排隊模型.

2.1 銀行排隊系統的M/M/C排隊模型

假設銀行排隊系統中設有C個服務窗口，所以其服務臺為C個并聯的服務臺，顧客的到達時間間隔和服務時間均服從負指數分布，因此，可以將銀行服務系統構建為M/M/C排隊模型[3]，現將該模型具體描述如下：

(1)到達規則：顧客的到達時間間隔T服從泊松分布，即顧客的到達時間間隔服從參數為λ的指數分布，其分布函數為：FT(t)=1-e-λt(t≥0)，相繼兩位顧客的平均間隔時間為E(t)=1/λ，且顧客的到達是相互獨立的.

(2)排隊規則：顧客到達系統后，可選擇任一服務臺接受服務，若服務臺空閑，則可立即接受服務；若服務臺繁忙，則需排隊等待被服務，服務規則為先到先服務.(3)服務規則：設銀行柜員的平均服務率服從參數為μ的指數分布，服務時間V即對一顧客的服務時間，則服務時間V當顧客到達數n≥c時服從參數為cμ的指數分布，其分布函數為：Fv(t)=1-e-μt(t≥0)，顧客的平均服務時間為E(V)=1/cμ.

2.2 系統的狀態轉移圖及穩態方程組

在1個服務臺的情況下，系統的服務強度為ρ=λ/μ，而銀行排隊系統是多服務臺并聯的情況，因此ρ=λ/cμ.當ρ>1時，即到達率大于服務率，則系統會出現無限排隊的情況下，所以只有當時，系統才會達到穩態，分析可得穩態下系統的狀態轉移圖[4]如圖2所示：

圖2 M/M/C系統的狀態轉移圖Fig.2 State transition diagram of M/M/C system

由系統的狀態轉移圖，分析可得穩態下的狀態概率方程[5]

利用遞推法對上述概率方程進行求解，可得穩態下系統n個顧客數的概率：

(1)

2.3 系統的主要排隊指標

要研究銀行的優化窗口數，必須對系統的排隊隊長，顧客的等待時間等排隊指標進行分析.然后利用排隊論的相關理論進行分析，得到模型的優化解.

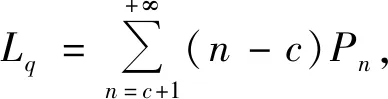
(2)

(2)系統的平均隊長

(3)

(3)顧客的等待時間：等待時間是指顧客從進入系統到服務完離開系統共用去的時間，由Little公式可得

(4)

(4)顧客的逗留時間

(5)

3 銀行排隊系統的優化

在該銀行排隊M/M/C模型中，顧客的到達和服務時間均是隨機的，但服務臺的c個數是可以設定的.顧客總是希望銀行能增加越多的服務窗口來減少他們的排隊等待時間，盡管增加服務窗口能提高銀行的服務效率，卻使銀行的成本費用大幅度增加.因此，在優化銀行排隊問題時，應兼顧客戶和銀行雙向需求，以費用作為目標函數，進行分析.

3.1 建立銀行服務窗口優化的目標函數

假設銀行排隊最優的服務窗口數為c0，建立費用函數Z=x0c+y0L(c)，以費用函數Z最小為目標函數，即銀行的服務成本和客戶的等待成本總和最小.其中，x0：單位時間每個服務臺的平均成本；y0：單位時間內每個顧客等待所消耗的費用；c：服務窗口數；L：系統的平均隊長.

3.2 邊際分析最優的排隊窗口數

要想滿足費用函數最小，利用邊際分析法[6]有

Z(c0-1)≤Z(c0)≤Z(c0+1)

將費用函數Z=x0c+y0L(c)代入，整理后得

(6)

4 實際數據分析

4.1 數據的采集與處理

以運城市建設銀行鹽湖支行為研究對象，通過對該行連續三周的客流量的觀察分析，發現該行一般在早上9:00～10:00和下午15:00～16:00客流量較大，分別選取客流量較大和客流量一般的兩個時間段進行分析，故選取9:00～11:00這個時間段進行觀察分析，每間隔10分鐘調查單位時間內到達的客戶數，得到的樣本數據見表1；同時，統計每位顧客的服務時間，即顧客從開始接受服務到服務完成離去的時間間隔，得到的樣本數據見表2.

表1 各時間段到達的顧客數Tab.1 Number of customers who arrive at each time

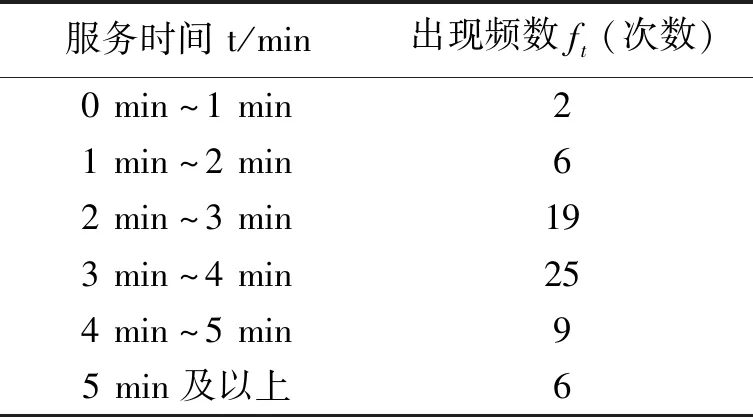
表2 顧客的服務時間統計Tab.2 Customer service time statistics

4.2 單位時間到達的顧客數服從分布的檢驗

從表1的數據可得，單位時間顧客的平均到達率：λ=5.583(人/10 min)=0.558 3(人/min).下面利用χ2擬合檢驗單位時間內顧客的到達數是否服從Possion分布[7]，數據結果見表3.

表3 χ2擬合檢驗顧客到達是否服從Possion分布Tab.3 χ2 fitting test whether customer arrival follows Possion distribution

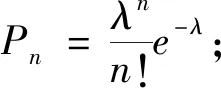
4.3 顧客服務時間服從分布的檢驗

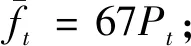
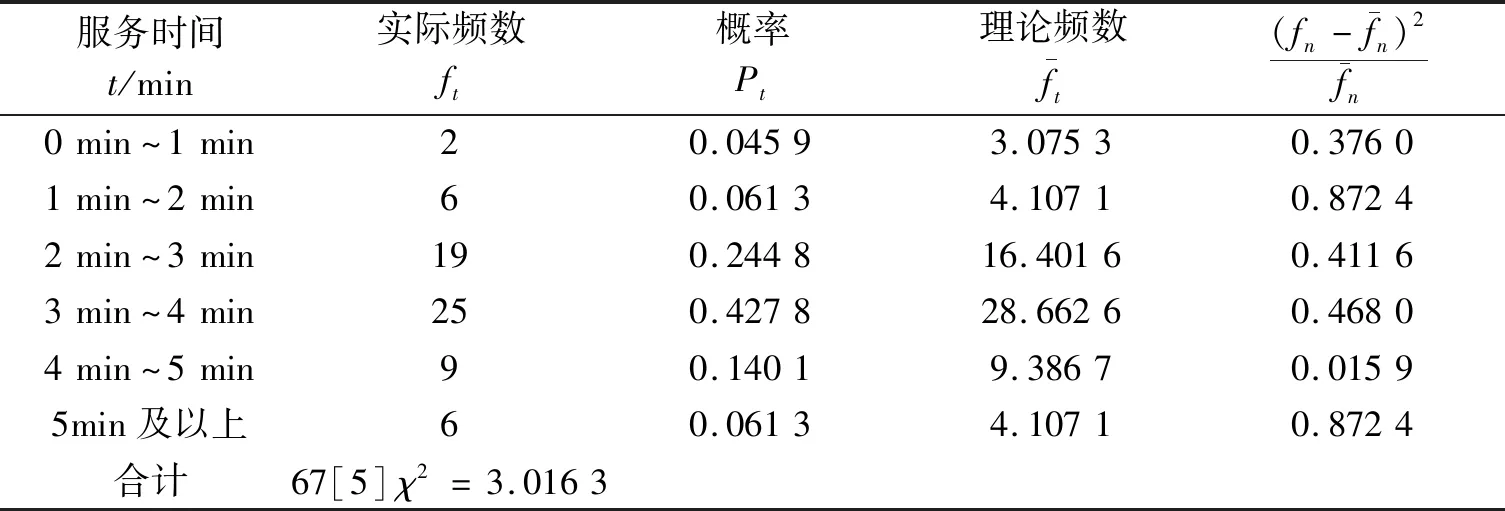
表4 擬合檢驗服務時間是否服從負指數分布 Tab.4 Fitting test whether service time is subject to negative exponential distribution

4.4 各項排隊指標計算值

由公式(1)～公式(5),代入參數λ=0.558 3，μ=0.306 6，當服務臺個數c取不同的值時，分別求出對應的排隊指標值.

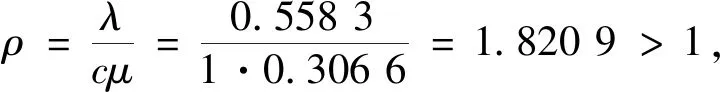
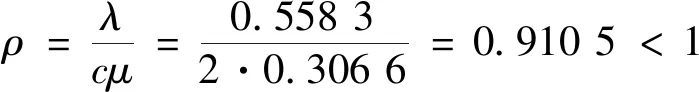
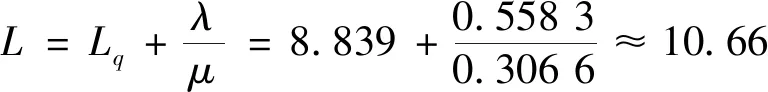
上述計算結果表明,當銀行設置2個業務窗口時，排隊等候的平均人數是9人，等候時間為15分鐘，可見排隊現象較嚴重，會增加客戶的不耐煩度.

按照如上的計算方式，設置業務窗口為c=3，c=4,c=5，計算各排隊指標，將計算結果列入表5.

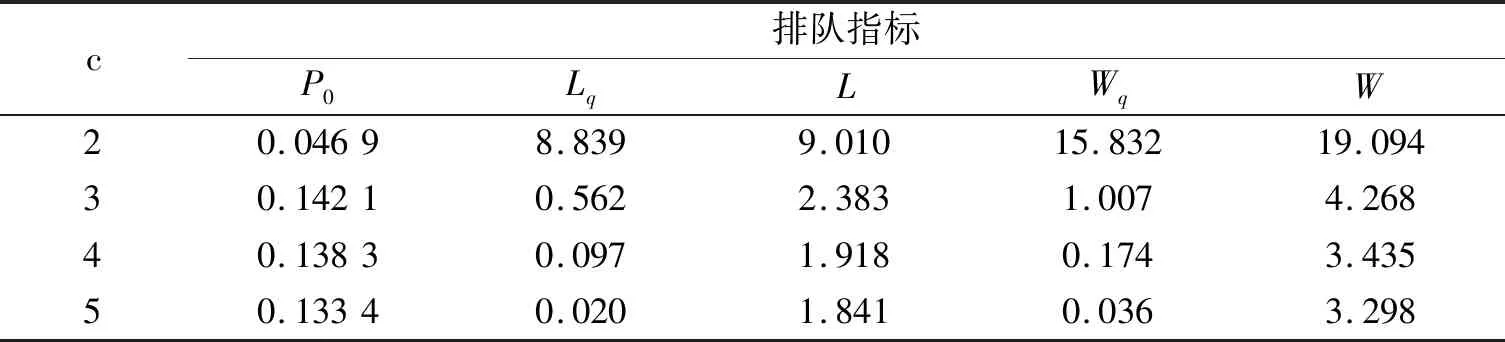
表5 各排隊指標計算值Tab.5 Calculated value of each queuing index

從表5可以看出，當業務窗口數從2個增加到3個后，減少的排隊人數為8.839-0.562=8.277，很好地緩解了客戶的排隊現象；而當窗口數繼續增加時，雖然也緩解了排隊人數，但成效不明顯.

4.5 銀行服務窗口優化分析

依據調查分析，假設每個窗口1分鐘的平均成本x0為1.1元，每個客戶等待1分鐘所消耗的費用為0.7元，由3.2節中建立的邊際分析最優的排隊窗口數模型，結合表5和式(6),得到的結果見表6.

通過計算x0/y0≈1.571，發現該值落在區間(0.465,6.627)，此時銀行開設的窗口數為3個.同時，由表6的最后一列也可知，當開設3個窗口時，總費用最小，即Zmin=z(3)=x0c+y0L=1.1×3+0.7×9.010=4.968 1.

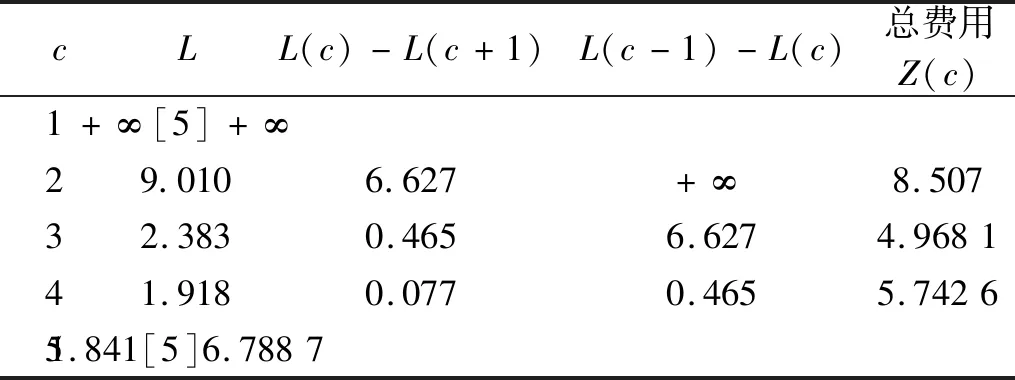
表6 排隊系統的總費用Tab.6 Total cost of queuing system

綜上所述，在該時間段內銀行開設c0=3個服務窗口時，既能滿足客戶的需求，也能使在此期間產生的運營成本和客戶的損失最小，達到銀行與客戶之間雙向利益的最佳平衡，此結論與該銀行當前的實際情況相符.

5 結論

本文基于排隊論的相關理論知識，對銀行服務窗口的優化設置進行研究.通過對銀行的實地調研分析，經過數據整理得到了銀行排隊模型中的相關參數，同時利用統計學中的相關知識對所求參數進行檢驗，保證了模型求解中參數的可靠性.在設置目標函數優化模型時，建立了銀行運營成本和客戶損失間的費用函數，并利用邊際分析法對該目標函數進行求解，驗證了最優的服務窗口數，使得銀行和客戶的雙方利益最大化.本文的求解方法具有普遍適用性，但此模型也是一種理想化的模型，實際問題中，還有很多特殊的因素需要考慮其中，因此，本文的研究結果和準確數值之間會存在一定誤差，但仍具有一定的理論參考價值.