彈性支承上簡支約束長矩形薄板面內剪切作用下屈曲行為分析

李君誼，莫時旭，鄭艷

(1.桂林理工大學土木與建筑工程學院，廣西 桂林541004；2.廣西建筑新能源與節能重點實驗室，廣西 桂林541004)

1 引言

在國家大力推行下，鋼-混組合結構在工程中得到廣泛應用。矩形鋼管混凝土在工程應用中，薄壁鋼板受彎矩和剪力同時作用，易發生局部屈曲；薄壁鋼-混凝土組合墻在抵抗水平作用時，鋼板受剪切作用，也會發生屈曲。彈性支承上矩形板面內受壓作用下的屈曲問題已有相關文獻，而彈性支承上矩形板面內剪切受力條件下的屈曲問題國內相關研究較少。實際工程中已知薄板剪切屈曲的臨界強度，可以避免其發生剪切屈曲，具有工程應用意義。

近年來，國內外學者對矩形薄板的屈曲問題進行了大量分析研究。國外學者Timshenko等[1]在能量法的基礎上提出了不同情況下矩形薄板的彈性屈曲理論計算模型；國內學者邊宇虹[2]用變分法對四邊簡支的矩形板的穩定問題進行了研究；莫時旭等[3]用Ritz能量變分法對方形鋼管混凝土局部屈曲問題進行了試驗研究；毛佳等[4]采用Ritz能量變分法對彈性支承上薄板屈曲進行了研究；童根樹等[5]采用有限元法對四邊簡支矩形板在各聯合作用下的彈性屈曲問題進行了研究分析；本文采用Rayleigh-Ritz法（瑞利-里茲法）推導了基于彈性基底的周邊簡支約束矩形板面內剪切受力條件下的屈曲理論計算公式，具有理論指導意義。

2 理論計算

Rayleigh-Ritz法，是應用勢能駐值原理求解穩定問題的一種很重要的近似方法，此法采用具有幾個廣義坐標的位移函數近似地代替真實的位移曲線，將原來為無限個變量的泛函變分問題變為有限個變量的函數極值問題來處理。根據勢能駐值原理的極值條件，用導數求極值問題的方法，可以將求解微分方程的問題變為求解代數方程的問題。

假設屈曲薄板的撓度曲面為下列級數形式：

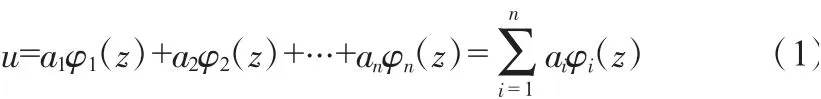
式中，ai為待定參變數，稱為廣義坐標，i=1,2,3,…,n；φi（z）為滿足幾何邊界條件的已知函數，z為自變量，φi為對應函數，這些函數任意選擇且線性無關。

將公式(1)代入總勢能∏=U+V的表達式，從而使總勢能變為具有n個參變數ai的函數。這樣，總勢能的∏變分δ∏，δ∏=δ（U+V）就可以用與各參變數變分ai相對應的增量之和來表達：

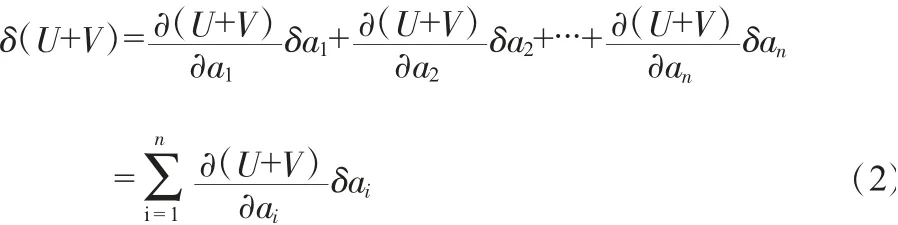
式中，∏為總勢能；U為彈性體應變能；V為外力勢能。

若彈性體系的變形處于平衡狀態，則應滿足勢能駐值條件，將公式（2）帶入δ∏=0，得：

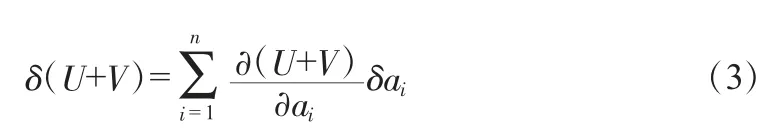
因為參變數ai變分是微小的任意數值，欲滿足式（3），只有：

從而得到下列方程組：

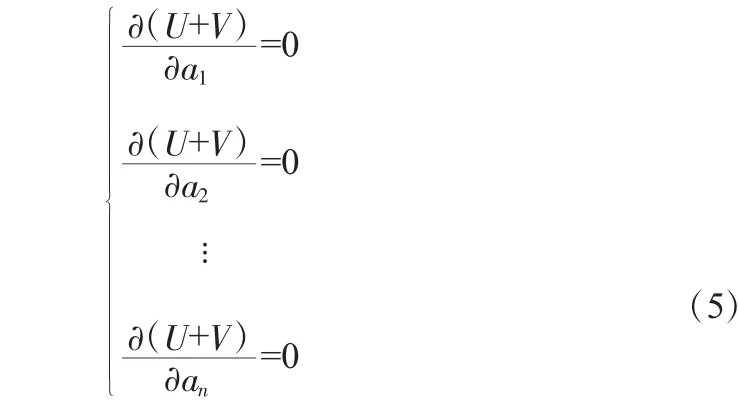
此方程組有非零解的條件為系數行列式等于零，從而得到穩定方程式。解此穩定方程，即可求得平衡狀態的荷載。

本文簡支邊界計算模型見圖1，矩形薄板受剪屈曲后縱向為連續n個半波，即為n階屈曲模態。

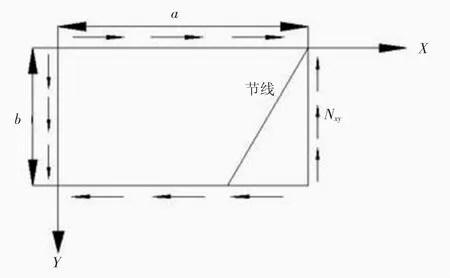
圖1 簡支邊界計算簡圖

取一階屈曲模態及二階屈曲模態研究具有代表性，因此取位移函數為：

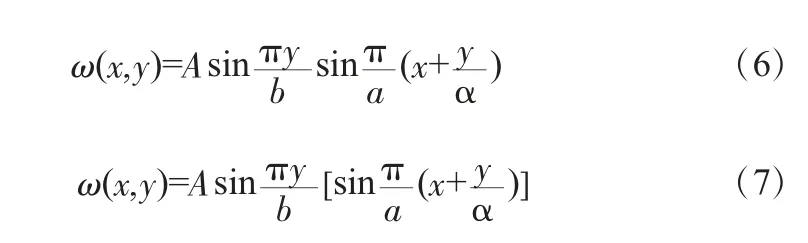
式中，A為位移函數中波長的振幅；a為矩形薄板長度；b為矩形薄板寬度；α為節線斜率；x、y分別為X方向和Y方向的分位移。

位移函數滿足上下邊界：

位移函數滿足節線邊界上：

式中，位移函數上下邊界滿足y=0，y=b時，位移函數ω(x,y)=0；節線邊界滿足ω對x求偏導數為0。

板彎曲應變能U、彈性支承勢能Uk和軸向載荷Nxy及軸向荷載做功V分別為：

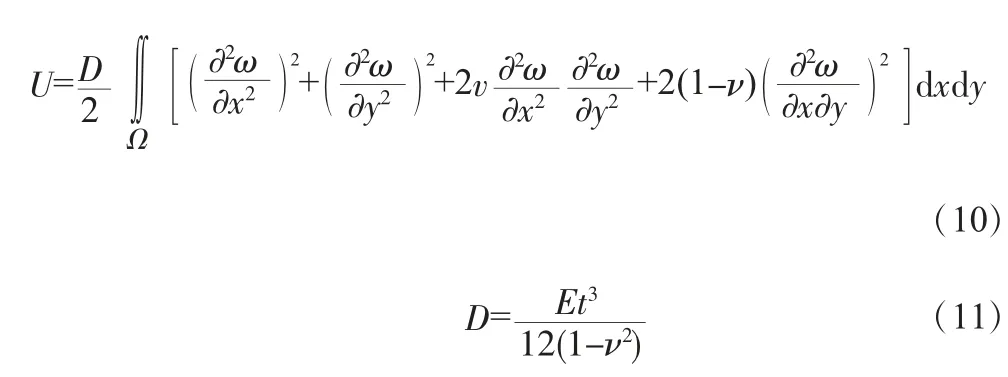
式中，U為板彎曲應變能；D為矩形薄板單寬抗彎剛度；E為鋼材彈性模量；t為薄板厚度；ν為鋼材泊松比。

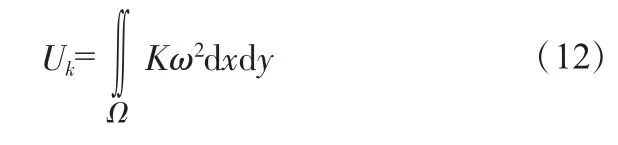
式中，Uk為彈性支承勢能；K為彈性支承剛度；ω為矩形薄板受剪屈曲后的位移函數ω（x，y）。

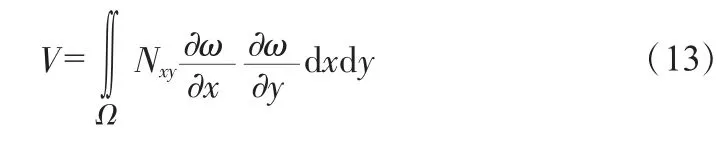
式中，V為軸向荷載做功；Nxy為軸向荷載。

根據最小勢能原理，可求得臨界狀態的軸向荷載：

式中，κ為屈曲系數；b為矩形薄板寬度。

3 參數影響分析

3.1 長寬比影響分析

假設彈性支承剛度K=0，取不同的長寬比γ（γ≥1.5），然后對節線斜率α求導，求出使屈曲系數κ取最小值的節線斜率α，最后帶入α得出臨界屈曲系數（見表1），臨界屈曲系數與不同長寬比的關系，如圖2所示。

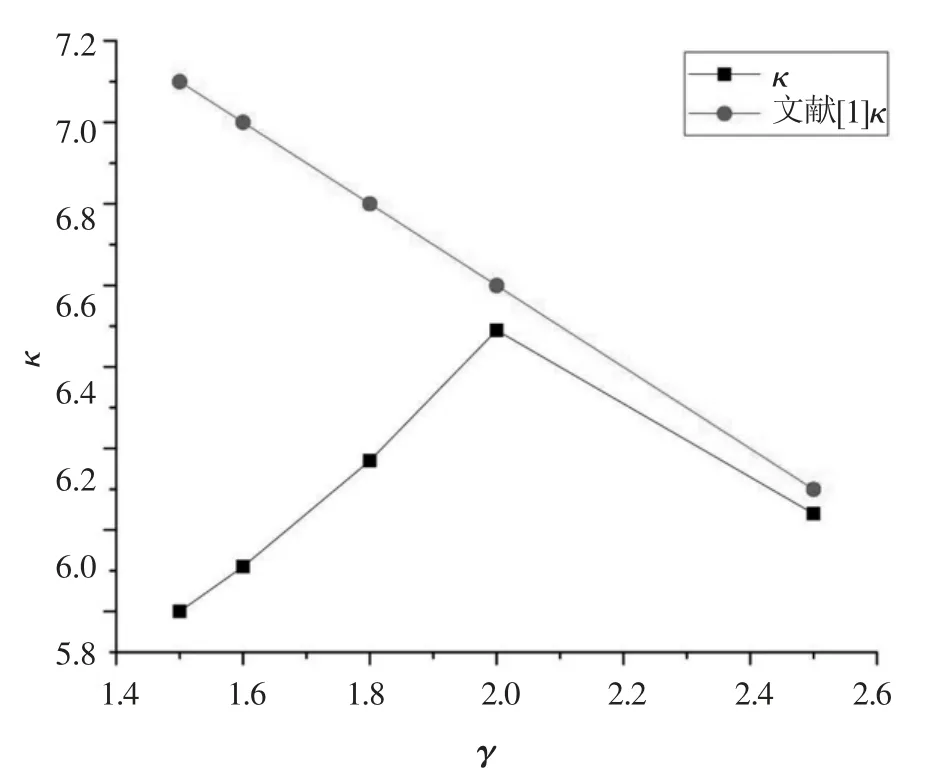
圖2 本文與文獻[1]簡支邊界κ-γ曲線

由表1可以得出：對于長矩形薄板（γ≥1.5），本文理論計算值與文獻[1]的計算值平均偏差為9.16%；對于長矩形薄板（γ≥2），偏差小于1.67%。在工程實際應用中長矩形薄板（γ≥2）的情況更多。

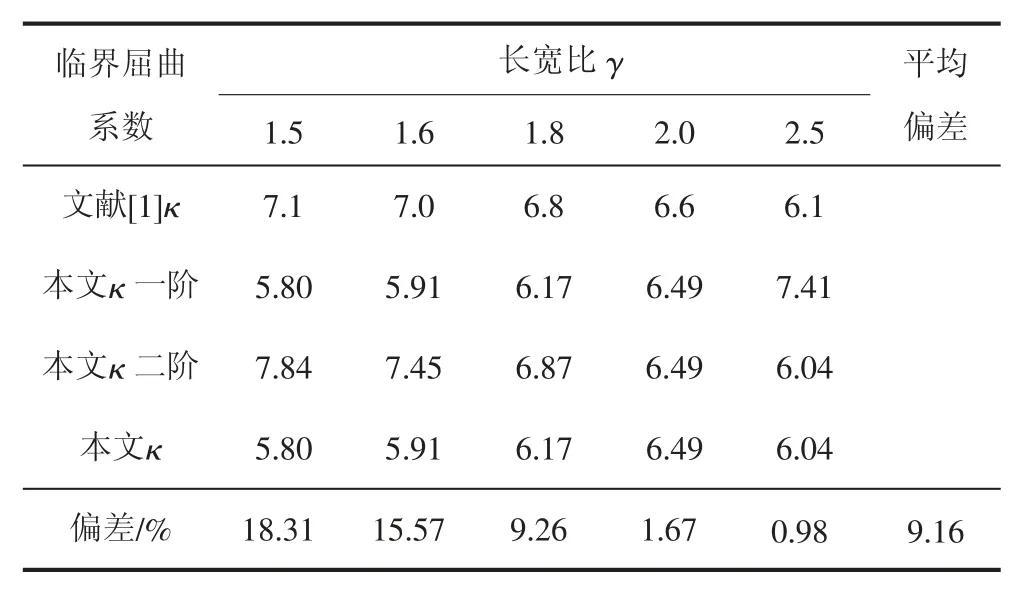
表1 簡支邊界下不同長寬比的臨界屈曲系數

3.2 支承剛度影響分析

假設矩形薄板長為2 m，寬為1 m（γ=2），即方形薄板；板厚為0.03 m；鋼材彈性模量為2.1×1011Pa；取不同的K，得出相應的臨界屈曲系數（見表2），臨界屈曲系數與支承剛度的關系如圖3所示。

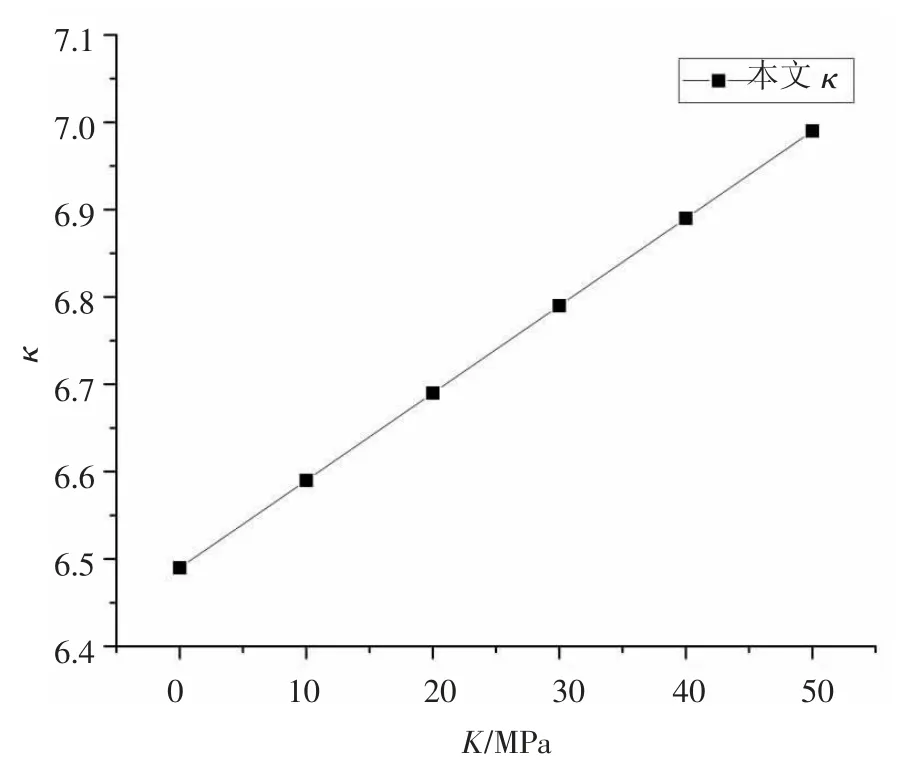
圖3 本文簡支邊界κ-K曲線

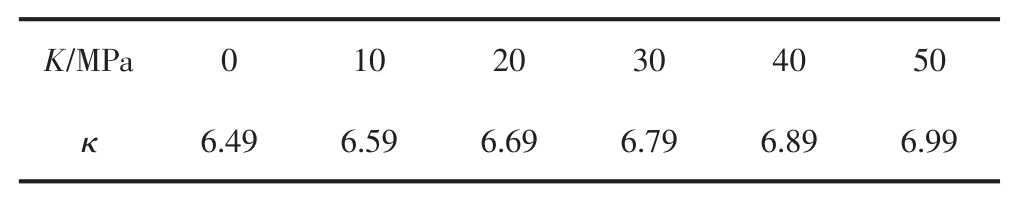
表2 簡支邊界下不同支承剛度的臨界屈曲系數

由圖3可以得出：臨界屈曲系數隨著支承剛度的單調遞增，即支承剛度越大，對長矩形薄板的側向約束越強，臨界屈曲系數越大。

4 結論

1）本文采用Rayleigh-Rite法計算彈性支承上簡支約束長矩形薄板面內剪切作用下臨界屈曲系數，計算所得的臨界屈曲系數與文獻[1]計算所得數據略有偏差，證明此理論方法可行。

2）彈性支承的剛度越大，對長矩形薄板的側向邊界約束越強，長矩形薄板屈曲越困難。

3）對于高階屈曲形態的長矩形薄板，如縱向屈曲為n個斜向半波，可假設函數為來求解，從而得出在不同長寬比下完整的臨界屈曲系數曲線。