淺談大數(shù)定律教學(xué)設(shè)計(jì)

于淼　吳素文　宋贄　楊吉會　張闞

[摘 要]大數(shù)定律是概率論與數(shù)理統(tǒng)計(jì)課程中抽象難懂的重要教學(xué)內(nèi)容，如何設(shè)計(jì)與完備大數(shù)定律教學(xué)是課程教師實(shí)踐中不斷的追求。在教學(xué)積累過程中，以切比雪夫不等式為基礎(chǔ)，以依概率收斂概念為依托，介紹了大數(shù)定律的一般形式，給出了隨機(jī)事件頻率穩(wěn)定在其概率的精確表達(dá)，并探索服從大數(shù)定律的充分條件，找出大數(shù)定律之間的內(nèi)在聯(lián)系，從而培養(yǎng)學(xué)生的概率統(tǒng)計(jì)思維模式及理論聯(lián)系實(shí)際的應(yīng)用能力。

[關(guān)鍵詞]切比雪夫不等式;依概率收斂;大數(shù)定律;思維模式;應(yīng)用實(shí)踐

[中圖分類號] G642 [文獻(xiàn)標(biāo)識碼] A [文章編號] 2095-3437（2021）11-0079-04

在概率論與數(shù)理統(tǒng)計(jì)的課程教學(xué)中，大數(shù)定律既很重要又是難點(diǎn)，它以嚴(yán)格的數(shù)學(xué)形式， 表達(dá)了隨機(jī)現(xiàn)象最根本的性質(zhì)——平均結(jié)果的穩(wěn)定性，在理論與實(shí)踐中均有廣泛應(yīng)用[1]。它是承上啟下的教學(xué)內(nèi)容，既是前面概率論部分的必要補(bǔ)充，又為數(shù)理統(tǒng)計(jì)部分提供理論依據(jù)，被稱為“統(tǒng)計(jì)學(xué)的靈魂”[2]。由于大數(shù)定律理論性較強(qiáng)，內(nèi)容復(fù)雜，教學(xué)比較抽象與枯燥，且難于掌握和理解，因此更好地梳理與設(shè)計(jì)大數(shù)定律的教學(xué)內(nèi)容具有重要的理論與實(shí)踐意義。

一、知識復(fù)習(xí)與準(zhǔn)備

（一）切比雪夫（Chebyshev）不等式

設(shè)隨機(jī)變量X的數(shù)學(xué)期望和方差都存在，則對任意常數(shù)[ε>0]，有

[PX-E（X）≥ε≤D（X）ε2]，

或[PX-E（X）<ε≥1-D（X）ε2].[3]

切比雪夫不等式是大數(shù)定律的基礎(chǔ)，是證明大數(shù)定律的有力工具[4]，可以說，伯努利（Bernoulli）大數(shù)定律、切比雪夫大數(shù)定律、馬爾可夫（Markov）大數(shù)定律均是借助于切比雪夫不等式完成證明的，使用了[PX-E（X）<ε≥1-D（X）ε2]形式。

（二）依概率收斂

隨機(jī)變量序列[Xn]依概率收斂于X是指[limn→∞PXn-a<ε=1]，記作[Xn→Pa]，表示絕對偏離[Xn-a]小于任一給定量的可能性隨著n增大而愈來愈接近于1。

大數(shù)定律是一類定理的統(tǒng)稱，涉及的是依概率收斂問題。大數(shù)定律這節(jié)內(nèi)容包括大數(shù)定律的一般形式和四個常見的大數(shù)定律：伯努利大數(shù)定律、切比雪夫大數(shù)定律、馬爾可夫大數(shù)定律和辛欽（Khinchin）大數(shù)定律。

二、教學(xué)設(shè)計(jì)

（一）伯努利大數(shù)定律

1.背景

伯努利大數(shù)定律背景的介紹不僅可以使學(xué)生們知道定理的來龍去脈，更能提高他們的學(xué)習(xí)興趣與積極性，樂于跟隨教師走進(jìn)大數(shù)定律的抽象世界。歷史上第一個極限定理屬于伯努利，就是伯努利大數(shù)定律，其思想源于概率論與數(shù)理統(tǒng)計(jì)第一章中講到的事件發(fā)生的頻率隨著試驗(yàn)次數(shù)的增加穩(wěn)定在事件的概率，如多次拋擲一枚硬幣，正面向上與反面向上的頻率會穩(wěn)定在其概率0.5，最為著名的要數(shù)蒲豐投針實(shí)驗(yàn)。1777年，法國數(shù)學(xué)家蒲豐在一張白紙上畫出多條等距平行線，并將長度為平行線間距一半的2212枚針隨機(jī)投到白紙上，觀察到與平行線相交的針為704枚，由此得到圓周率π的近似值[π≈2212704≈3.142][5]。將頻率穩(wěn)定性給予精確地描述就是伯努利大數(shù)定律。

2.定理內(nèi)容及證明

伯努利大數(shù)定律闡述了事件發(fā)生的頻率依概率收斂于該事件的概率。

可以采用切比雪夫不等式來進(jìn)行證明，采用逆向思維，從結(jié)論入手，需要證明事件A的頻率[μnn]依概率收斂于其概率[P（A）=p]，即[limn→∞Pμnn-p<ε=1]。考慮到與切比雪夫形式的一致性，如果頻率[μnn]本身是一個隨機(jī)變量，且概率p是該隨機(jī)變量的期望就好了。而頻數(shù)[μn]是n重伯努利試驗(yàn)中事件A出現(xiàn)的次數(shù)，確實(shí)是隨機(jī)變量，服從二項(xiàng)分布[B（n，p）]，期望[E（μnn）=p]，方差[D（μnn）=p（1-p）n]。現(xiàn)在要證[limn→∞Pμnn-p<ε=1]，已知[Pμnn-p<ε≤1]，由切比雪夫不等式[Pμnn-p<ε=Pμnn-E（μnn）<ε≥1-D（μnn）=1-p（1-p）nε2]，再根據(jù)夾逼準(zhǔn)則得證。

3.應(yīng)用

用蒙特卡羅（Monte Carlo）方法之隨機(jī)投點(diǎn)法計(jì)算定積分[J=01f（x）dx， 0≤f（x）≤1]。

（二）大數(shù)定律的一般形式

伯努利大數(shù)定律給出了頻率穩(wěn)定性的精確表述，其實(shí)大量測量值的算術(shù)平均值即樣本均值同樣也具有穩(wěn)定性，這種穩(wěn)定性是大數(shù)定律存在的客觀背景[6]。

從伯努利大數(shù)定律引出大數(shù)定律的一般形式：頻數(shù)[μn～B（n ， p）]，而二項(xiàng)分布可以看成是有限個相互獨(dú)立的兩點(diǎn)分布之和，即[μn=i=1nXi]，[Xi～B（1， p）]。此時[E（μnn）=E（1ni=1nXi）=p]，可得

[limn→∞P1ni=1nXi-E（1ni=1nXi）<ε=1]，記樣本均值[X=1ni=1nXi]，得到結(jié)論樣本均值[X]依概率收斂于樣本均值的期望[E（X）]，也就是總體均值[E（X）]，即[X→PE（X）]。

由此給出了大數(shù)定律的一般形式：對任意的[ε>0]，有[P1ni=1nXi-1ni=1nE（Xi）<ε=1]，即

[1ni=1nXi→P1ni=1nE（Xi）]。

大數(shù)定律反映了大樣本條件下平均結(jié)果的穩(wěn)定性，為人類世界提供了一個基本規(guī)律：在一個包含眾多個體的大群體中，由于偶然性個體間會產(chǎn)生差異，但是在大數(shù)定律的作用下，整個群體卻能呈現(xiàn)出某種穩(wěn)定的狀態(tài)[7-8]。當(dāng)然，在樣本容量擴(kuò)大的過程中，樣本均值序列偏離總體均值的機(jī)會始終存在，但會隨著樣本容量的擴(kuò)大而減小，當(dāng)樣本容量達(dá)到一定程度時，樣本均值依概率收斂于總體均值，樣本均值近似看作總體均值[9]。

在理解了大數(shù)定律的結(jié)論后，我們想要知道在什么情況下隨機(jī)變量序列會服從大數(shù)定律，即服從大數(shù)定律有哪些充分條件。為此，我們繼續(xù)學(xué)習(xí)切比雪夫大數(shù)定律、馬爾可夫大數(shù)定律和辛欽大數(shù)定律。它們從不同的角度給出了服從大數(shù)定律的條件。

（三）切比雪夫大數(shù)定律

1.條件

切比雪夫給出了服從大數(shù)定律需要滿足兩個條件：一是隨機(jī)變量序列[Xn]兩兩不相關(guān);二是[D（Xn）]存在且有共同的上界，即[D（Xn）≤c]，c為常數(shù)。

2.定理證明

仍從結(jié)論入手，需要證明

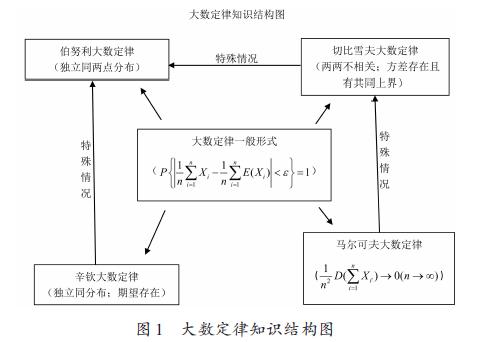
[P1ni=1nXi-1ni=1nE（Xi）<ε=1]。仍然借助切比雪夫不等式，得[P1ni=1nXi-1ni=1nE（Xi）<ε≥1-D（1ni=1nXi）ε2]，因?yàn)閇Xn]兩兩不相關(guān)，且[D（i=1nXi）=i=1nD（Xi）+2Ci

3.伯努利大數(shù)定律與切比雪夫大數(shù)定律的關(guān)系

伯努利大數(shù)定律是切比雪夫大數(shù)定律的特例。伯努利大數(shù)定律滿足切比雪夫大數(shù)定律的兩個條件：頻數(shù)可以看成是有限個相互獨(dú)立的兩點(diǎn)分布之和，即隨機(jī)變量序列[Xn]獨(dú)立同參數(shù)為p的兩點(diǎn)分布。獨(dú)立自然兩兩不相關(guān)，滿足條件一;兩點(diǎn)分布的方差為[p（1-p）]，方差存在且相等，有共同的上界，滿足條件二。

4.推論

如果隨機(jī)變量序列[Xn]獨(dú)立同分布，且方差有限，則[Xn]服從大數(shù)定律。在證明切比雪夫大數(shù)定律的過程中，我們發(fā)現(xiàn)其實(shí)只需要當(dāng)[n→∞]時[D（1ni=1nXi）=1n2D（i=1nXi）]的極限為0即可，這正是由切比雪夫的學(xué)生馬爾可夫給出的大數(shù)定律的條件。

（四）馬爾可夫大數(shù)定律

1.條件

馬爾可夫大數(shù)定律只要求滿足一個條件：[1n2D（i=1nXi）→0（n→∞）]，稱為馬爾可夫條件。

由此可見，馬爾可夫大數(shù)定律對隨機(jī)變量序列[Xn]沒有任何同分布、獨(dú)立性、不相關(guān)的假設(shè)，使用起來比較簡單，因此應(yīng)用較多。

2.應(yīng)用舉例

設(shè)[Xn]為同一分布、方差存在的隨機(jī)變量序列，且[Xn]僅與[Xn-1]和[Xn+1]相關(guān)，而與其他的[Xi]不相關(guān)，試問該隨機(jī)變量序列[Xn]是否服從大數(shù)定律？

3.切比雪夫大數(shù)定律與馬爾可夫大數(shù)定律的關(guān)系

切比雪夫大數(shù)定律是馬爾可夫大數(shù)定律的特例。從切比雪夫大數(shù)定律的證明過程來看，切比雪夫的兩個條件都是為了得到馬爾可夫條件，進(jìn)而服從大數(shù)定律。

（五）辛欽大數(shù)定律

1.條件

辛欽大數(shù)定律也要滿足兩個條件：一是隨機(jī)變量序列[Xn]獨(dú)立同分布;二是[E（Xn）]存在。

這與切比雪夫大數(shù)定律的推論相比，條件一相同，條件二將方差簡化為了期望，使用起來更加簡便。切比雪夫與馬爾可夫大數(shù)定律中都對方差做了要求，辛欽大數(shù)定律只需考慮期望。

辛欽大數(shù)定律的證明借助于特征函數(shù)的概念，在課上未對學(xué)生進(jìn)行講解，一方面由于特征函數(shù)理論涉及復(fù)數(shù)，相對較難，另一方面也容易打破知識結(jié)構(gòu)的系統(tǒng)性。

2.應(yīng)用舉例1

將教材中應(yīng)用切比雪夫大數(shù)定律推論的例子放到此處，并且可以去掉一個已知條件[E（X4n）<∞]，應(yīng)用辛欽大數(shù)定律得到相應(yīng)結(jié)論。

設(shè)隨機(jī)變量序列[Xn]獨(dú)立同分布，若令[E（Xn）=μ，D（Xn）=σ2]，考察[Yn=（Xn-μ）2， n=1， 2， …]是否服從大數(shù)定律？

3.應(yīng)用舉例2

用蒙特卡羅方法之平均值法計(jì)算定積分[J=01f（x）dx，0≤f（x）≤1]。

4.伯努利大數(shù)定律與辛欽大數(shù)定律的關(guān)系

伯努利大數(shù)定律是辛欽大數(shù)定律的特例。伯努利大數(shù)定律中，隨機(jī)變量序列[Xn]獨(dú)立同參數(shù)為p的兩點(diǎn)分布，滿足辛欽大數(shù)定律的兩個條件，條件一獨(dú)立同分布，條件二兩點(diǎn)分布的期望存在，為其參數(shù)p。

三、知識總結(jié)

大數(shù)定律這節(jié)主要介紹了大數(shù)定律的一般形式，即隨機(jī)變量的樣本均值依概率收斂于總體均值;還講述了四個大數(shù)定律，其中伯努利大數(shù)定律精確解釋了頻率的穩(wěn)定性，而其他三個大數(shù)定律分別給出了服從大數(shù)定律的充分條件，并且四個大數(shù)定律之間具有內(nèi)在聯(lián)系。講授過程中步步深入，逐漸展開，自然過渡，銜接流暢，富于邏輯性，有助于學(xué)生的消化理解及整體性的把握。本節(jié)要求掌握與理解大數(shù)定律的基本理論，并能應(yīng)用大數(shù)定律完成相關(guān)問題。圖1為本節(jié)的知識結(jié)構(gòu)圖。

四、結(jié)論與討論

（一）注重教學(xué)過程中思維模式的培養(yǎng)

概率論與數(shù)理統(tǒng)計(jì)是高校十分重要的基礎(chǔ)課程，也是當(dāng)代數(shù)學(xué)最為活躍的分支之一，是研究隨機(jī)現(xiàn)象統(tǒng)計(jì)規(guī)律性的一門學(xué)科，經(jīng)常采用大量實(shí)驗(yàn)與觀測的方式找出與分析事物間的內(nèi)在規(guī)律性，因此培養(yǎng)學(xué)生的概率直覺思維能力與統(tǒng)計(jì)辯證思維方法顯得尤為重要[10]。

大數(shù)定律表明大量隨機(jī)現(xiàn)象由于偶然性相互抵消而呈現(xiàn)出必然數(shù)量規(guī)律[11]。它是“算術(shù)平均值法則”的理論基礎(chǔ)[12]，是概率論與數(shù)理統(tǒng)計(jì)課程的精華所在。然而由于大數(shù)定律較強(qiáng)的理論性及學(xué)習(xí)的困難性，很多教師將該節(jié)內(nèi)容不講或略講，使學(xué)生不能完整構(gòu)建概率統(tǒng)計(jì)的思維邏輯并完成從概率論到數(shù)理統(tǒng)計(jì)的順利過渡，更談不上對于大數(shù)定律理論聯(lián)系實(shí)際的應(yīng)用。客觀世界中充滿了不確定性，但要從中找到確定性，大數(shù)定律的思維模式必不可少，相對于“小數(shù)”，“大數(shù)”更具理論與應(yīng)用價(jià)值，為實(shí)際生產(chǎn)生活提供了必不可少的理論依據(jù)和方法論，是大數(shù)據(jù)分析中海量與多樣化的信息運(yùn)用的前提之一。同時，大數(shù)定律所蘊(yùn)含的概率統(tǒng)計(jì)思想也體現(xiàn)出做事鍥而不舍、知難而進(jìn)的寶貴精神品質(zhì)，讓學(xué)生們在學(xué)習(xí)知識的過程中體會與完善人格魅力。

（二）課上適量進(jìn)行理論知識拓展

課上講授的大數(shù)定律給出了服從大數(shù)定律的充分條件，在其他情況下是否也會得出服從大數(shù)定律的結(jié)論，也就是是否存在其他的充分條件。茆詩松等編寫的《概率論與數(shù)理統(tǒng)計(jì)教程第二版》大數(shù)定律一節(jié)的習(xí)題中又給出了三個大數(shù)定律，這里是要完成對它們的證明，自然也可以讓同學(xué)們在完成習(xí)題的基礎(chǔ)上學(xué)習(xí)與理解這三個大數(shù)定律，包括泊松（Poisson）大數(shù)定律、伯恩斯坦（Bernstein）大數(shù)定律與格涅堅(jiān)科（Gnedenko）大數(shù)定律。對于感興趣的學(xué)生還可以自己查閱資料或探索其他充分條件。

（三）開展課外應(yīng)用實(shí)踐活動

現(xiàn)實(shí)生活中，人們很多時候都會有意或無意的運(yùn)用大數(shù)定律理論方法。例如人們在實(shí)際觀測中，往往并不是只做一次觀測得到觀察值，而是大量重復(fù)觀測后取平均值作為真實(shí)值[13]。

授課過程中舉了兩個應(yīng)用蒙特卡羅方法的例子——分別用伯努利大數(shù)定律和辛欽大數(shù)定律計(jì)算定積分。蒙特卡羅方法也稱為隨機(jī)模擬方法，是一種大數(shù)收斂的數(shù)值計(jì)算方法，依據(jù)概率論與數(shù)理統(tǒng)計(jì)理論知識建立模型并借助于現(xiàn)代計(jì)算機(jī)技術(shù)來實(shí)現(xiàn)算法，再經(jīng)大量隨機(jī)仿真而形成真實(shí)值的逼近[14]。蒙特卡羅方法不僅可以實(shí)現(xiàn)定積分的計(jì)算，還可以求解不規(guī)則圖形的面積[15]，也可以在蒲豐投針實(shí)驗(yàn)思想指導(dǎo)下，利用Matlab軟件模擬計(jì)算圓周率π的近似值[5]。

大數(shù)定律是保險(xiǎn)業(yè)和彩票業(yè)存在和發(fā)展的數(shù)理基礎(chǔ)。例如它是保險(xiǎn)公司收取保費(fèi)的理論依據(jù)，保險(xiǎn)公司利用“個別情形存在的不確定性將會在大數(shù)中消失”的規(guī)則，可將個別風(fēng)險(xiǎn)單位遭遇損失的不確定性轉(zhuǎn)化為風(fēng)險(xiǎn)單位集合損失的確定性[16]。

教師可以給學(xué)生布置課外應(yīng)用實(shí)踐的任務(wù)，以小組為單位，查閱資料，總結(jié)或?qū)崿F(xiàn)大數(shù)定律的實(shí)際應(yīng)用過程。不僅可以使學(xué)生更好地掌握和理解大數(shù)定律理論知識，同時可以在應(yīng)用中找到課程學(xué)習(xí)的重要意義。

[ 參 考 文 獻(xiàn) ]

[1] 李伯德.大數(shù)定律在重積分中的一些應(yīng)用[J].蘭州商學(xué)院學(xué)報(bào)，1988（2）：64-69.

[2] 邱志平.大數(shù)定律教學(xué)設(shè)計(jì)探究[J].教育教學(xué)論壇，2016（3）：153-155.

[3] 茆詩松，程依明，濮曉龍.概率論與數(shù)理統(tǒng)計(jì)教程第二版[M].北京：高等教育出版社，2018：12.

[4] 沈偉利.談切比雪夫不等式的應(yīng)用[J].鄭州鐵路職業(yè)技術(shù)學(xué)院學(xué)報(bào)，2005（1）：24-25.

[5] 李娜，王丹齡.大數(shù)定律的教學(xué)設(shè)計(jì)研究[J].高師理科學(xué)刊，2017（9）：74-76.

[6] 許芳忠，許金華.大數(shù)定律及中心極限定理的教學(xué)課程設(shè)計(jì)探討[J].科技資訊，2010（36）：227.

[7] 李蕊.淺談幾個著名的大數(shù)定律及應(yīng)用[J].科學(xué)咨詢（科技管理），2010（12）：64-65.

[8] 于進(jìn)偉，趙舜仁.大數(shù)定律與中心極限定理之關(guān)系[J].高等數(shù)學(xué)研究，2001（1）：15-17.

[9] 楊小勇，王興福.重視銜接，兼顧情感：“大數(shù)定律與中心極限定理”的教學(xué)思考[J].數(shù)學(xué)教學(xué)研究，2011（10）：50-51.

[10] 賈天理，李春濃，黃金華，等.大數(shù)定律應(yīng)用問題分析與概率直覺思維培養(yǎng)[J].綿陽師范學(xué)院學(xué)報(bào)，2010（2）：6-9.

[11] 王昕，程希明.概率論與數(shù)理統(tǒng)計(jì)案例教學(xué)方法探析[J].沈陽師范大學(xué)學(xué)報(bào)（自然科學(xué)版），2013（3）：372-375.

[12] 羅弟亞.大數(shù)定律和中心極限定理的可視化（教學(xué)）[J].四川工業(yè)學(xué)院學(xué)報(bào)，2000（1）：70-75.

[13] 王成，鄒海雷，銀俊成.概率論教學(xué)探討：重視概念理解[J].商情，2011（16）：30.

[14] 車金星.蒙特卡洛計(jì)算方法及其在定積分求解中的應(yīng)用[J].考試周刊，2011（88）：71-72.

[15] CR勞.統(tǒng)計(jì)與真理——如何運(yùn)用偶然性[M].北京：科學(xué)出版社，2019：8-9.

[16] 趙國棟.大數(shù)定律的生活體現(xiàn)[J].教育界，2016（24）：152.

[責(zé)任編輯：林志恒]