阻尼環車輪對鋼軌波磨的影響*

楊普淼 張銀仙 許 巖 楊布雷 陳光雄

(西南交通大學摩擦學研究所 四川成都 610036)

我國地鐵行業飛速發展，極大地提高了城市交通運輸效率，但隨之而來的鋼軌波浪形磨損(波磨)現象困擾了研究人員多年[1]。列車通過有波磨鋼軌路段時，輪對垂向力急劇變化，發生強烈的振動和噪聲，影響車輛旅客乘坐的舒適度和車輛平穩性能，嚴重時導致脫軌等惡性交通事故發生[2]。波磨極大地影響了列車安全性能，國內外研究人員提出了許多抑制波磨的措施。GRASSIE[3]將波磨分類為P2共振波磨、車轍波磨、其他P2共振波磨、重載波磨、輕軌波磨和特定軌道結構波磨，并提出了不同解決辦法。OOSTERMEIJER[4]指出改變鋼軌材料屬性能抑制波磨產生。VADILLO等[5]研究指出加設軌枕能抑制短波波磨產生。QIAN等[6]研究證實敷設鋼軌阻尼減振器能有效抑制鋼軌波磨的產生。崔曉璐等[7]研究了改變輪軌系統結構參數對波磨的影響，并提出最優結構參數。近年來，陳光雄教授提出了輪軌系統摩擦自激振動引起鋼軌波磨的理論，并已得到國內外研究人員的認同[7-12]。

隨著我國材料行業的飛速發展，材料性能得到了很大的提高。阻尼材料因其特殊減振性能[13]而逐漸被軌道交通研究人員使用。阻尼車輪應運而生，如，扣件阻尼墊、阻尼環[14]、車輪輻板阻尼涂層[15-16]等。其中，因為阻尼環安裝簡便(能直接鑲嵌在輪輞上)，對車輪結構改動小而受到研究者和施工人員的青睞。日本車輪公司設計了橡膠包夾鋼材質阻尼環，已用于實際生產。但關于阻尼環對鋼軌波磨的影響研究還很少見到報道。

本文作者基于陳光雄教授[6]提出的摩擦自激振動理論，建立了牽引輪對-鋼軌-軌枕組成的有限元模型[17]，模擬車輛穩態通過小半徑(R≤350 m)曲線軌道工況，采用ABAQUS經典有限元復特征值算法進行了計算預測。文中首先通過與實測數據對比，驗證了無阻尼環輪軌模型的正確性；然后在該模型車輪輪轂處添加阻尼環，對比研究有無阻尼環、阻尼環阻尼系數(β)、阻尼環安裝位置以及單側阻尼環寬度對鋼軌波磨的影響。

1 模型的建立

1.1 輪軌模型

設定車輛穩態通過曲線半徑小于350 m軌道，并以此建立牽引輪對-鋼軌-軌枕三維有限元模型，進行仿真計算。車輪選用LM踏面，車輪直徑840 mm；鋼軌總長36 m；扣件間距625 mm，扣件類型選用DTVI2。車輛通過小半徑曲線時，左右輪軌接觸位置和接觸角差異較大，高軌接觸角約32°，低軌接觸角約2.1°，如圖1所示。

圖1中，δR、δL分別為低軌和高軌輪軌接觸角；FSVL、FSVR為輪對垂向懸掛力；FSLL、FSLR為輪對橫向懸掛力；KRV、KRL、KSV、KSL分別為扣件垂向和橫向剛度、軌枕垂向和橫向剛度；CRV、CRL、CSV、CSL分別為扣件垂向和橫向阻尼、軌枕垂向和橫向阻尼。其中，KRV=8.79 MN/m，KRL=40.73 MN/m，KSV=340.136 MN/m，CRV=6 361.29 N·s/m，CRL=1 927.96 N·s/m，CSV=CSL=0.027 54 N·s/m，有限元模型如圖2所示。

圖1 輪軌接觸位置、接觸角和蠕滑力方向Fig 1 Wheel-track contact position,contact angle and creep force direction

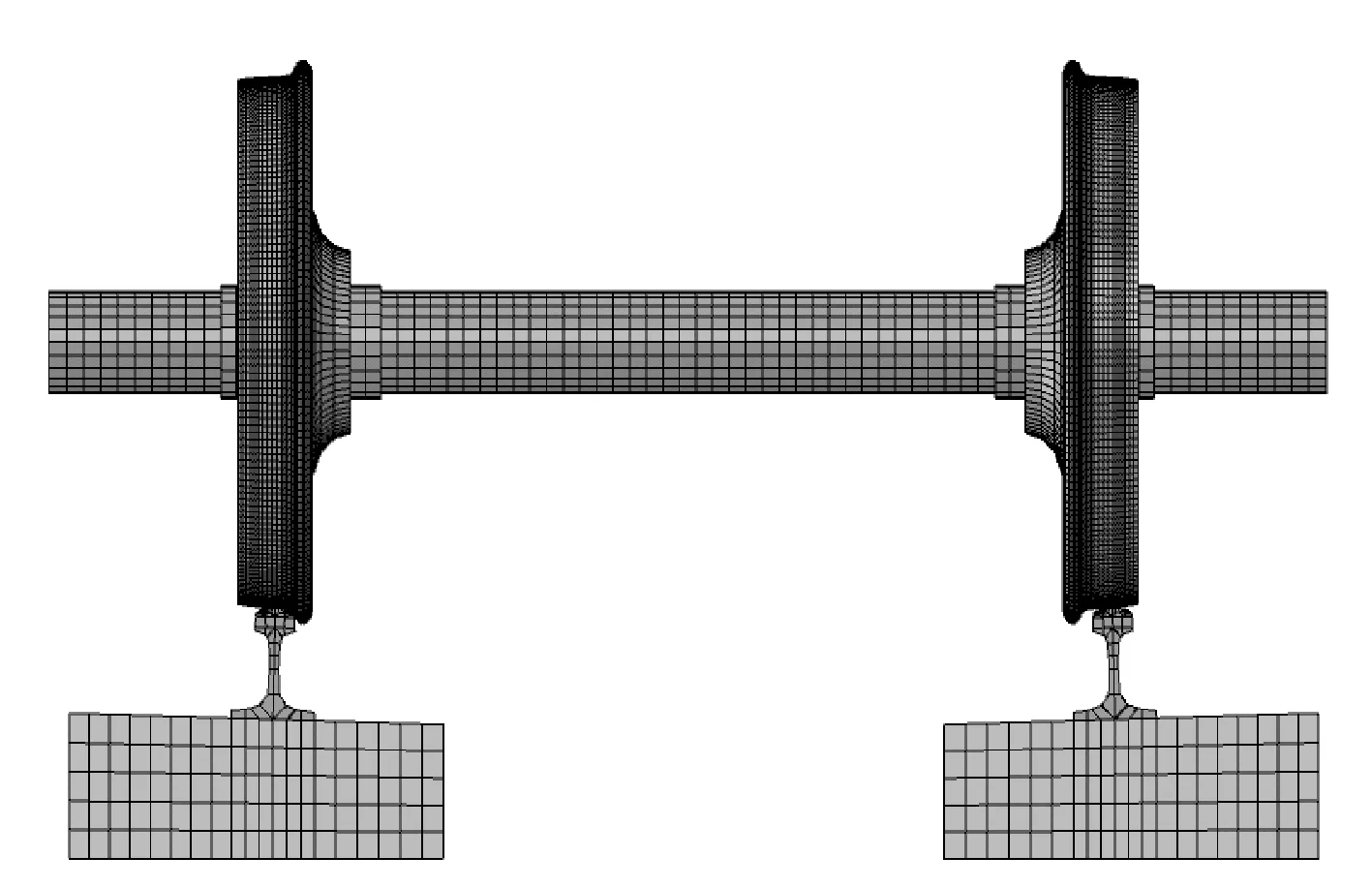
圖2 有限元模型Fig 2 Finite element model

為討論阻尼環安裝位置對波磨的影響，將阻尼環分別安裝在外側、軸側和雙側(外側和軸側同時安裝)，如圖3所示。實際安裝時阻尼環是鑲嵌在輪輞中，文中為研究方便，進行了適當簡化，將阻尼環貼放在輪輞邊緣。

圖3 阻尼環模型Fig 3 Damping ring model

1.2 復特征值理論分析

有限元分析中，復特征值法能預測系統發生摩擦自激振動頻率和模態，故文中采用該方法預測不穩定振動趨勢。假設兩接觸面(主面、從面)部分網格節點重合，在考慮摩擦力的前提下，對重合節點進行力學平衡計算，得到如下表達式：

(1)

式中：?表示位移；M表示質量矩陣；C表示阻尼矩陣；K表示剛度矩陣。

忽略摩擦力時，質量、阻尼、剛度矩陣都是嚴格對陣矩陣。加入摩擦力后，質量、阻尼、剛度矩陣都將變為非對稱矩陣。對公式(1)進行特征方程改寫，得到以下公式：

(M(γn)2+C(γn)+K)σn=0

(2)

其中，γn是公式(2)求解的特征值，σn是公式(2)特征值對應的特征向量。σn可記作：

σn=αn+jβn

(3)

式中：αn是特征向量的實部，βn是特征向量的虛部，j為虛數。

對該特征向量進行多次迭代計算，得到第i階模態。所以，當特征向量實部為正時，計算得到模態不收斂，即系統容易發生不穩定振動。但是一些實部為正，絕對值很小的特征向量，也不能引起系統不穩定振動。為了更準確地評定系統狀態，引入等效阻尼比來表示系統是否存在不穩定振動，其計算公式為

ζ=-2αn/(|βn|)

(4)

式中：ζ是等效阻尼比。

當ζ為負時，系統發生不穩定振動，且絕對值越大，發生不穩定振動的趨勢越強，文中使用該指標來判斷系統是否有發生摩擦自激振動趨勢。

2 計算結果及分析

2.1 有無添加阻尼環模型分析

根據陳光雄教授提出的摩擦自激振動理論，當車輛通過小半徑(R≤350 m)曲線，導向輪對中內輪蠕滑力飽和，容易引起摩擦自激振動。有限元模型模擬車輛通過小半徑曲線的計算結果如圖4所示。無阻尼環中，等效阻尼比ζ最小為-0.023 78，對應頻率為502.32 Hz。線路實測波磨頻率為200～1 000 Hz[18]，地鐵通過小半徑曲線時速約55 km/h。根據速度、波長和頻率關系[19]，得到波長約為30.4 mm，符合線路實測數據。該頻率對應的模態如圖5所示，外軌幾乎沒有變形，內軌發生嚴重變形。這表明當系統發生摩擦自激振動時，內軌產生波磨而外軌不會產生波磨，這點與線路實況高度吻合，所以文中模型能用于預測波磨計算。

圖5 頻率f=502.32 Hz時無阻尼環輪對的模態(ζ=0.023 78)Fig 5 Mode of the wheelset without damped ring at frequency of 502.32 Hz(ζ=0.023 78)

文中所有阻尼環材料參數采用ABAQUS中的瑞利阻尼[20]，α=0、β=1×10-5。后文所有計算材料參數，如未特殊說明，都取該數值。由圖4可以看出，當車輪外側添加阻尼環以后，得到阻尼比ζ=-0.021 22，f=512.99 Hz。最小等效阻尼比對應的頻率差異不大，絕對值有一定的減少，根據公式(4)可得，絕對值越小，系統發生不穩定振動的趨勢越小，從該對照組可以得出輪對添加阻尼環能一定程度上抑制輪軌系統波磨產生。這是因為，波磨是一種輪軌低頻不穩定振動現象，當輪軌接觸部位產生不穩定振動時，由于輪輞材質較硬，阻尼環硬度低，阻尼環將會發生變形；阻尼材料兩邊所受合應力相互抵消，故能起到減振吸振效果，能吸收一部分不穩定振動源的能量，即抑制波磨產生。

圖4 有、無阻尼環輪對時頻率-等效阻尼比關系Fig 4 Relationship between frequency and equivalent damping ratio of wheelset with and without damping ring

2.2 外側阻尼環阻尼系數對鋼軌波磨的影響

分別取阻尼系數β為1×10-6、1×10-5、1×10-4和1×10-3，研究輪對外側阻尼環阻尼系數β對輪軌系統波磨發生趨勢的影響，結果如圖6所示。4組阻尼系數值對應的模型等效阻尼比都大于無阻尼環模型的等效阻尼比值，這說明添加不同阻尼系數的阻尼環都能降低波磨產生的趨勢。當阻尼系數β的數量級為10-6和10-5時，系統都存在2個負等效阻尼比，等效阻尼比系數分別為-0.022 23和-0.021 22，數值差異不大，如圖7所示。阻尼系數的量級達到10-4和10-3時，與前兩組對比，等效阻尼比增加了9倍左右且只存在一個負等效阻尼比，如圖8所示。

圖6 等效阻尼比隨阻尼系數β的變化Fig 6 Variation of equivalent damping ratio with damping coefficient β

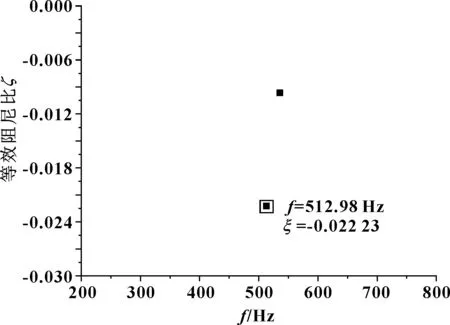
圖7 β=1×10-6時頻率-等效阻尼比關系Fig 7 Relationship between frequency and equivalent damping ratio at β=1×10-6

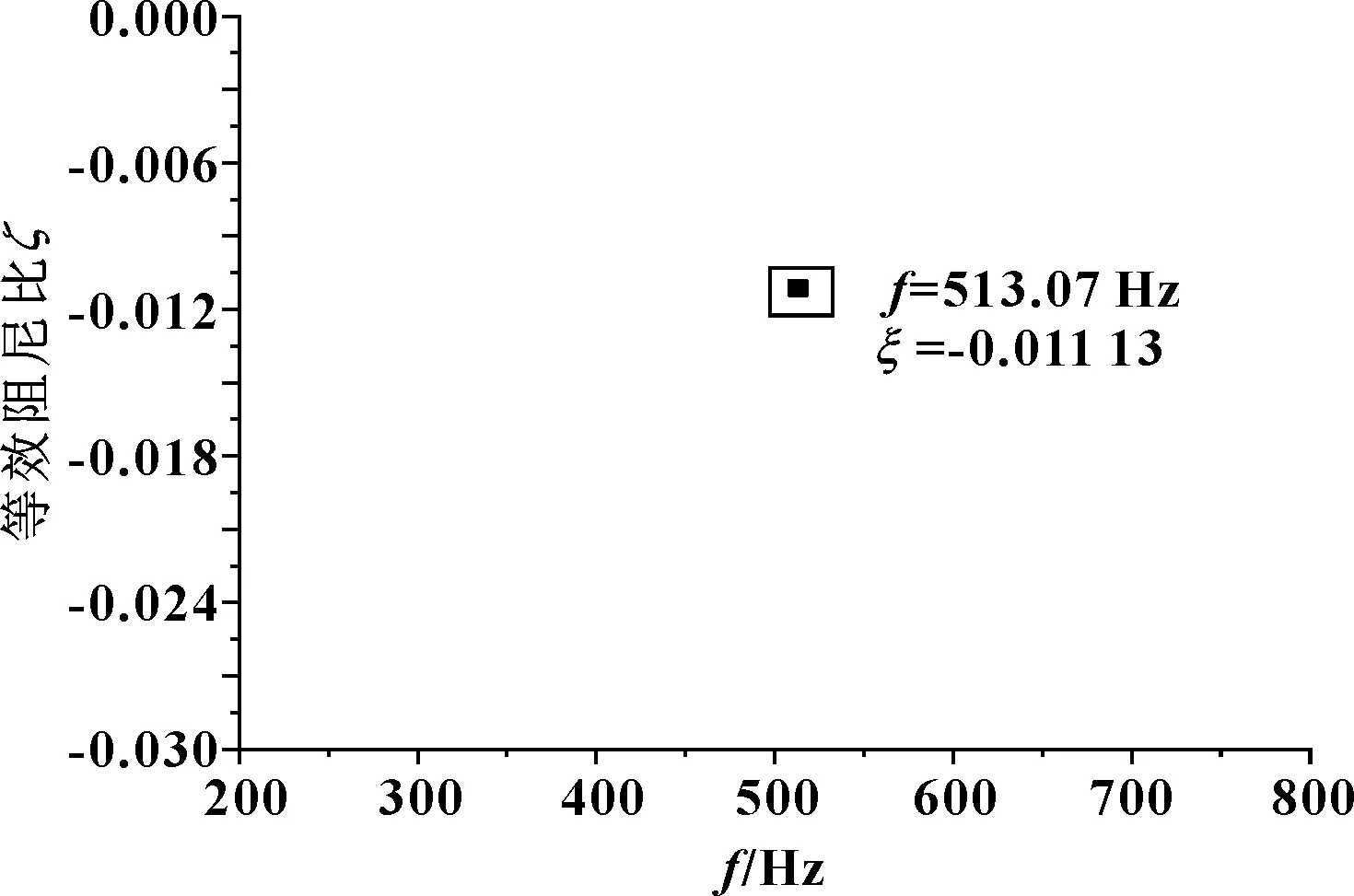
圖8 β=1×10-4時頻率-等效阻尼比關系Fig 8 Relationship between frequency and equivalent damping ratio at β=1×10-4

在β=1×10-3時，模型無負等效阻尼比(此處為方便表示，將該ζ記為0)，表示輪對在通過小半徑曲線時，不會產生任意頻率的摩擦自激振動，理論上能完全抑制波磨的產生，如圖9所示。阻尼系數β代表材料的吸振抗振能力，研究表明隨β的數量級提升，阻尼材料的減振性能逐漸升高，吸收不穩定振動能力增強。模型抑制波磨發生的能力逐漸增加。當β數量級為10-4和10-3時，系統穩定性有顯著提高。

圖9 β=1×10-3時頻率-等效阻尼比關系Fig 9 Relationship between frequency and equivalent damping ratio at β=1×10-3

2.3 單側、雙側添加阻尼環模型穩定性分析

阻尼環安裝位置分為外側、軸側和雙側，如圖3所示。3組模型計算結果如圖10所示。

圖10 阻尼環不同安裝位置的等效阻尼比計算結果Fig 10 Calculation results of equivalent damping ratio at different installation sites

在軸側添加阻尼環后，進行復特征值計算，得到等效阻尼比ζ=-0.020 68，f=510.12 Hz。相比外側安裝阻尼環計算得到的ζ=-0.021 22，等效阻尼比絕對值在減小，系統發生不穩定振動的可能性有所降低。雙側(外側和軸側)添加阻尼環后，計算發現ζ=-0.020 27，f=518.12 Hz，軸側添加阻尼環，等效阻尼比絕對值又有所減小，系統穩定性更好一些。

可見，外側、軸側和雙側添加阻尼環后，利用阻尼材料的減振特性，吸收振源能量，三者在不同程度上才能抑制波磨的產生和發展。3種阻尼環安裝位置的等效阻尼比雖呈上升趨勢，但等效阻尼比差異在0.001左右，對系統穩定性影響的差異不大。

2.4 單側不同阻尼環幾何尺寸對波磨的影響

設置阻尼環截面為矩形(如圖11所示)，且矩形寬度D分別為16 、18.5、21 cm，研究軸側阻尼環幾何尺寸對波磨的影響，計算結果如圖12所示。D=16 cm時，ζ=-0.020 46，f=511.46 Hz；D=18.5 cm時，ζ=-0.020 68，f=510.12 Hz；D=21 cm時，ζ=-0.020 53，f=514.83 Hz。可見，三者的等效阻尼次差異在0.000 1量級。據此得到，軸側不同阻尼環尺寸對輪軌系統穩定性的影響大致相同，但抑制鋼軌波磨能力都高于無阻尼環輪軌模型，與2.3節所得結論類似。

圖11 阻尼環截面圖Fig 11 The cross section of damping ring

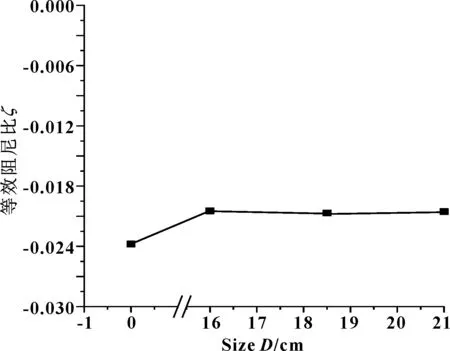
圖12 軸側不同寬度阻尼環的等效阻尼比計算結果Fig 12 Calculation results of equivalent damping ratio of damping ring on axis side with different width

設置矩形寬度D分別為17、19.5 和22 cm，研究外側阻尼環不同寬度對系統穩定性的影響，計算結果如圖13所示。矩形寬度為17 cm時，ζ=-0.021 63，f=511.46 Hz；矩形寬度為19.5 cm時，ζ=-0.021 22，f=512.99 Hz；矩形寬度為22 cm時，ζ=-0.021 58，f=511.12 Hz。可見，隨阻尼環寬度的增大，ζ絕對值先減小后增大，當D=19.5 cm時，ζ絕對值最小，系統穩定性最高，該寬度為外側阻尼環的最優尺寸。波磨大多發生小半徑曲線內軌，其接觸狀態如圖1所示，輪軌接觸位置相對更靠近外側阻尼環，系統整體穩定性對外側阻尼環結構變更為敏感，所以外側阻尼環結構變化更能影響系統穩定性。

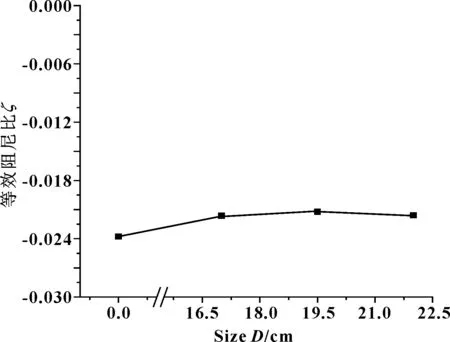
圖13 外側不同寬度阻尼環的等效阻尼比計算結果Fig 13 Calculation results of equivalent damping ratio of damping ring on outer side with different width

3 結論

(1)地鐵通過小半徑曲線(R≤350 m)時，內軌的蠕滑力飽和，有極大的可能性發生摩擦自激振動，即發生波磨。輪對添加阻尼環后，能有效減緩鋼軌波磨的發生趨勢。

(2)阻尼環車輪抑制波磨產生趨勢的能力隨著阻尼系數β的增大而增大。β=1×10-3時，阻尼環輪軌模型能完全抑制波磨的產生。

(3)外側、軸側和雙側3種安裝位置的阻尼環都能有效減緩鋼軌波磨的產生，但不同安排位置對鋼軌發生趨勢的抑制能力差別不大。

(4)安裝在軸側的阻尼環，其寬度變化時抑制車輪波磨的能力沒有明顯差別。安裝在外側的阻尼環，其寬度增加時，抑制車輪波磨的能力呈先增加后減小的趨勢，存在最優的阻尼環寬度(如文中的寬度19.5 mm)，使得阻尼環車輪的波磨抑制能力最佳。