淺海聲場中時頻互譜估計目標的絕對速度

趙安邦， 宋鵬飛， 惠娟1,， 郎俊杰

(1.哈爾濱工程大學 水聲技術重點實驗室,黑龍江 哈爾濱 150001； 2.哈爾濱工程大學 水聲工程學院,黑龍江 哈爾濱 150001； 3.西藏大學 工學院,西藏 拉薩 850000； 4.中國電子科技集團公司第五十四研究所,河北 石家莊 050081)

淺海低頻海洋信道具有穩定的干涉結構，其中包含了許多環境參數和目標運動信息，目標運動速度參數的獲取是海洋目標檢測、估計和定位的重要環節。對于單水聽器被動測距而言，互譜法是估計目標徑向運動速度常采用的方法。

文獻[1-4]都是采用互譜測速，利用得到的徑向速度信息進一步處理得到目標距離。這種方法無需聲場先驗信息，寬容性較高，有較高的發展應用潛力。另外，目標絕對速度參數是表征目標運動的一個物理量，也是被動聲吶目標識別的重要特征之一。運動目標的速度估計在被動聲吶信號處理中占據重要作用。

Rakotonarivo等[1]提出了單水聽器互譜測速的基本原理與測量方法，并以此給出了2種目標距離的被動估計算法。在此基礎上王鵬等[2]將其算法拓展應用到水平陣的被動目標互譜測速并且進行了隨機相位擾動補償，可以在更低的信噪比情況下進行互譜測速。邵云生等[3]利用水平線陣獲得波束域信號，對不同時刻波束域聲場的互相關信號進行頻譜分析估計運動目標速度值，并且進行了基于聲速擾動統計量的隨機相位擾動補償，可以在相對較低信噪比情況下獲得運動目標徑向速度值。王超等[4]則將文獻3的相位補償方法改進到單水聽器互譜測速中，以此來獲得更好的處理結果。

以上文獻可以看到互譜測速的發展其實都是對傳統互譜測速的原理進行一些補償或者應用范圍的拓展，并沒有對互譜測速的原理算法進行更深的探究和拓展。

而本文進一步從原理上拓展了互譜的變化規律，根據目標接近最近通過點過程中，其線譜信號互譜的變化規律，提出了時頻互譜測速算法，能夠在更高的信噪比增益條件下，利用WVD變換測量目標的絕對速度。

1 時頻互譜獲得目標速度的基本原理

根據淺海聲場簡正波表達式，將海洋波導看作是距離無關的水平分層環境，只考慮聲速和密度隨深度z的變化，將聲源視為點源，可以得到一般情況下，由連續譜和離散譜組成的聲場表達式[5]：

(1)

離散成分表示為海水中傳播的簡正波部分，而連續成分表示主要在海底傳播的側面波部分。當聲波遠距離傳播時，側面波的貢獻可以忽略不計。

將式(1)簡化得到：

其中：

(2)

式中:φ0表示初始相位；φnoise(t)是雜波和噪聲引起的相位起伏分量，聲速剖面存在聲速擾動時，存在隨距離變化的相位擾動φ(r)，該相位擾動由于聲速在距離上的擾動引起，會對簡正波波數產生影響，并且可通過聲速剖面的一階、二階統計量進行相對補償。

假定目標做勻速直線運動，在t1、t22個時刻處目標與水聽器相隔的距離分別為r1、r2。則其聲壓信號可以分別表示為：

(3)

將式(3)進行聲壓信號的互譜可以得到：

Ic(Δt,f)=p(t1,f)·p*(t2,f)≈

(4)

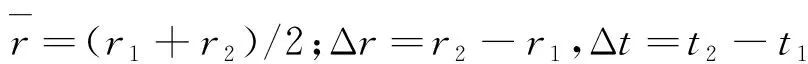
因此，可以將式(4)進一步整理化簡，對于目標在Δt的時間間隔內，從t1時刻運動到t2時刻，目標與水聽器之間的距離由r變為r+Δr，可以得到：

Ic(Δt,f)=Re[p(r+Δr)p*(r)]≈

(5)

式(5)可以看出，互譜隨著Δr的變化規律而變化，通過探究Δr與目標速度的關系即可實現目標徑向速度的估計。

對于勻速直線運動的目標，其絕對速度為一定值，如下圖所示，目標做勻速直線運動，航向角恒定為θ，目標運動過程中與水聽器的最近距離定義為r0，通過最近距離處的時刻定義為t0，對于任意時刻t目標距離水聽器距離r，目標的絕對速度為v，以水聽器為坐標原點。

而當目標遠離最近通過點時，即徑向速度沒有迅速變化時，則在時間間隔內目標的距離變化為：Δr=vr·Δt。

Ic(Δt,f)=Re[p(r+Δr)p*(r)]≈

(6)

對于Δr可以進一步簡化為：

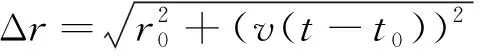
(7)

假定最近通過時刻設為初始t=0時刻，并進行泰勒展開取其前2項可以得到：

Δr=v2·t2/2r0

(8)

將式(8)代入到式(5)可以得到：

Ic(Δt,f)=Re[p(r+Δr)p*(r)]≈

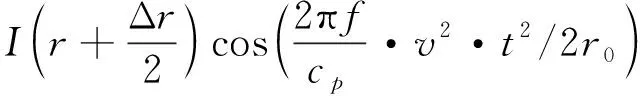
可以看出, 各Mach數下, H=0.8δ 渦流發生器使附面層厚度減小30%左右, 減小量小于H=1.2δ 渦流發生器. 圖7為尾渦誘導速度ω沿流向分布, 后緣高度H=0.8δ時尾渦強度較弱, 影響區域僅達到距試驗段入口4 m左右. 因此, 為充分發揮渦流發生器作用, 葉片后緣高度須略高于當地附面層厚度.

(9)

因此對于接近最近通過點的互譜呈現線性調頻信號的形式，因此可以通過時頻分析方法提取相關參數，得到目標的v2/r0。

式(6)的處理方法已在文獻[1]中敘述，本文主要討論式(9)，對于接近最近通過點處目標的線譜進行互譜計算，獲得其呈現線性調頻信號的形式，可以通過時頻分析方法提取其目標的v2/r0。對干涉條紋進行Hough變換[6-9]估計目標的v/r0[6]，利用估計目標的v2/r0和v/r0就可以進一步計算目標的絕對速度和最近通過距離，而目標任意時刻的距離也可以根據式(7)來進行估計。

而如果干涉條紋不清晰，可以通過互譜結合時頻分析，并將其計算結果代入到式(6)進一步計算此時刻的徑向速度，結合目標運動幾何關系：

(10)

也可以得到目標的絕對速度和最近通過距離。

2 仿真數據處理

仿真條件：海深200 m，在海水中聲速為1 500 m/s，密度為1 g/cm3，海底聲速為1 800 m/s，密度為1.8 g/cm3，點源位于水下4 m，水聽器位于水下30 m，聲源頻率范圍為40～640 Hz，目標以2.5 m/s的速度航行，與接收水聽器的最近通過距離為708 m，首先利用Kraken仿真模型得到目標運動LOFAR圖。

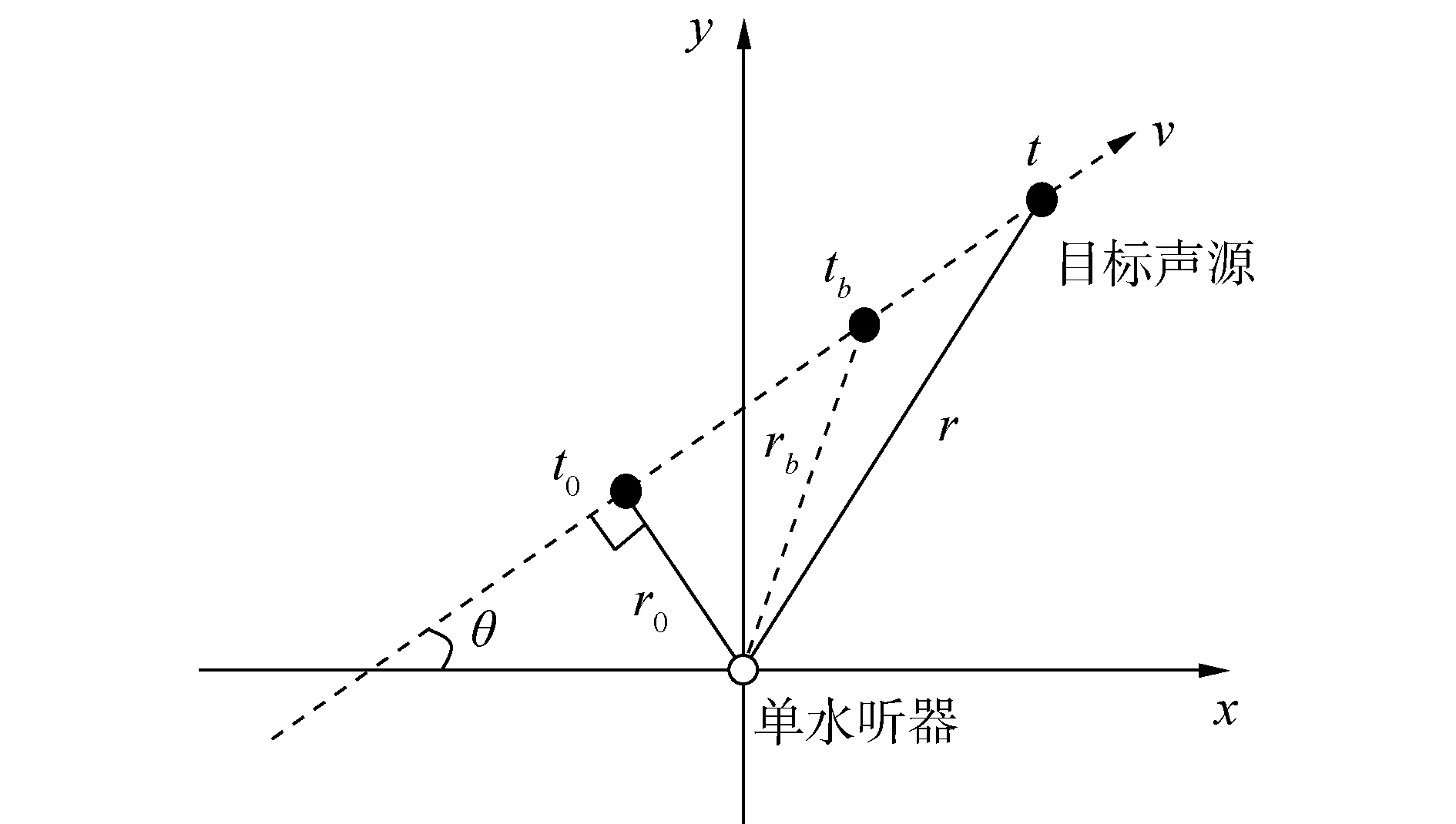
圖1 目標運動Fig.1 Target movement trend

圖2 運動目標LOFARFig.2 LOFAR map of moving target

采取其49 Hz處的頻譜信息，在1 000 s～1 400 s處進行互譜得到目標互譜圖如圖3所示。

從圖3中可以看到目標最近通過距離處的線譜互譜運算得結果呈現線性調頻信號變化，正如式(9)所示，對圖3的計算結果進行WVD變換[10-13]得到廣義時頻圖如下所示：

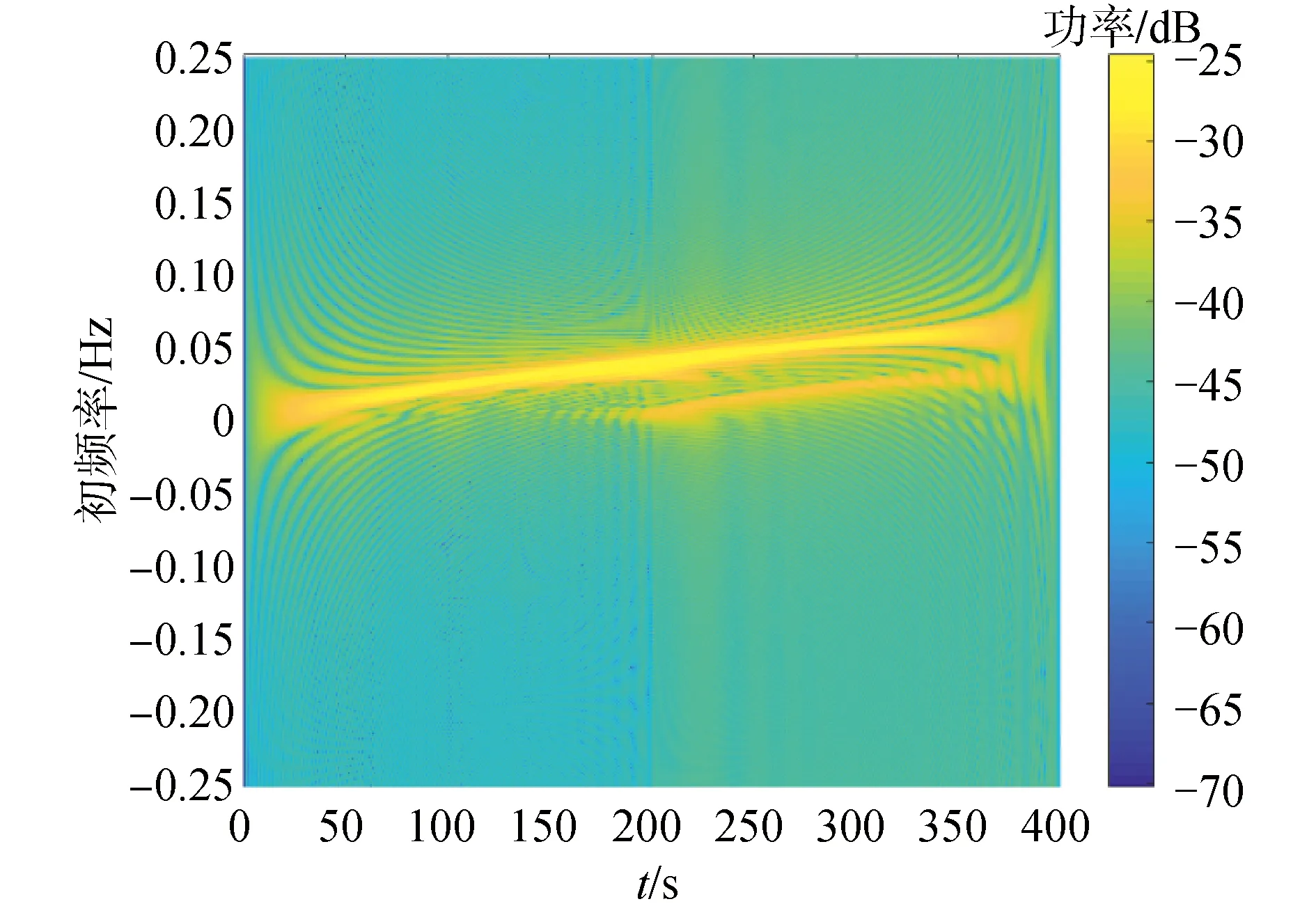
圖4 目標互譜的WVD變換Fig.4 WVD transformation of target cross spectrum

方法1 利用圖5搜尋到的峰值點代入式(9)計算目標的v2/r0估計值為0.008 5，將圖2進行Hough變換得到v/r0為0.003 4，進一步可以得到目標的絕對速度估計值為2.51 m/s，最近通過距離為735 m。絕對速度的估計誤差為0.4%，最近通過距離的誤差為2.4%。采用此算法可以得到較為理想的絕對速度和距離的估計結果。

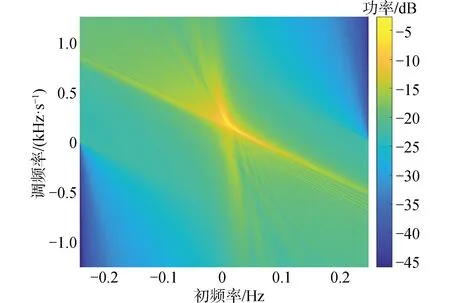
圖5 目標互譜的R-WVD變換Fig.5 R-WVD transformation of target cross spectrum

方法2 如果只有線譜信息，將v2/r0估計值結合式(10)，得到v/r0為0.003 6，估計的絕對速度為2.36 m/s，最近通過距離為655 m，絕對速度的估計誤差為5.6%，最近通過距離的誤差為7.4%。

以上為仿真計算得出的結果可以驗證2種算法的有效性，由于方法2只利用線譜信息，所以誤差較大。

3 SWellEx-96海上試驗數據處理

3.1 試驗概況

SWellEx-96試驗[14]是加利福尼亞大學Scripps海洋研究院于1996年5月10日-1996年5月18日，距離加利福尼亞圣地亞哥附近的洛馬角的尖端約12 km進行的聲學試驗。聲源為拖曳式聲源，發射信號為50～400 Hz的線譜或有一定帶寬的信號。SWellEx-96試驗中部署的聲學傳感器包括：垂直線陣VLA，傾斜的線陣TLA，安裝在海底的2個水平陣列HLA，分為北部和南部HLA。數據主要為S5、S59兩組。

S5中，聲源拖曳在一條等深線上，整個試驗過程沒有大的干擾物出現。聲源拖曳船從所有基陣的南側以5 kn(2.5 m/s)的速度向北行駛，大部分聲源拖曳海區的深度為180～220 m，另一半試驗的聲源是沿180 m等深線進行拖曳的。

有深(J-15)、淺(J-13)2個聲源，深的聲源拖曳深度大約54 m，它發射49～400 Hz多條線譜。淺聲源的拖曳深度大約9 m，它發射109～385 Hz的9個頻率，編號為C-109-9S。

3.2 試驗數據處理

如圖6所示，為S5實驗的HLA North陣列的接收數據進行分析，目標距離陣的最近通過距離708 m，圖7為某接收陣元的聲壓信號進行短時傅里葉變換得到的目標LOFAR圖。

圖6 試驗布置Fig.6 Test layout

圖7 接收陣元LOFARFig.7 LOFAR of receiving element

采取其49 Hz處的頻譜信息，在1 200 s～1 600 s處進行互譜得到目標互譜圖如圖8所示。

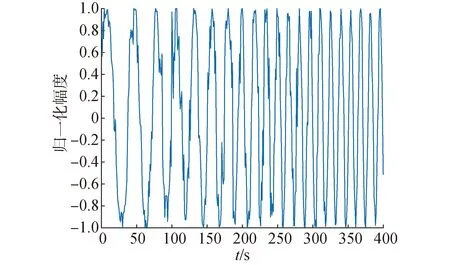
圖8 線譜49 Hz運動目標互譜Fig.8 Moving target cross spectrum of 49 Hz line spectrum

對圖3進行WVD變換得到的廣義時頻圖如圖9所示。

圖9 目標互譜的WVD變換Fig.9 WVD transformation of target cross spectrum

通過圖10可以獲得調頻率為0.000 151，代入到式 (9)計算目標的v2/r0估計值為0.009 27，將圖9與式 (6)聯立可得300 s時目標徑向速度為1.84 m/s，將其代入式 (10)計算v/r0為0.003 7，進一步可以計算目標的絕對速度估計值為2.5 m/s，最近通過距離為675 m。估計的絕對速度和最近通過距離誤差都在10%以內。并且對比常規互譜的輸出信噪比，由于時頻互譜可以無視徑向速度的變化，因此可以一次處理更長的接收信號，所以可以獲得更高的信噪比增益。

圖10 目標互譜的R-WVD變換Fig.10 R-WVD transformation of target cross spectrum

3.3 試驗數據增益分析

通過時頻互譜得到的輸出信噪比由于其積分時間更長，所以獲得的輸出信噪比增益更大[15-16]，在各向同性白噪聲背景中，其積分時間長度與增益的關系如下式所示：

G=5lgT

(11)

通過圖11與圖12對比可以得到，圖12的輸出干擾更小，圖11是每100 s進行一次傳統互譜測速得到的目標徑向速度估計圖，圖12是用本文提出的算法，由于不受徑向速度變化的限制，所以可以將所有采樣點一次處理，圖12的時間積分長度是圖11的4倍，通過計算得到圖11平均輸出信噪比比圖12的輸出信噪比低2 dB，其理論值為5lg4≈3.01 dB，可以得到通過本文的算法可以得到更高的信噪比增益。

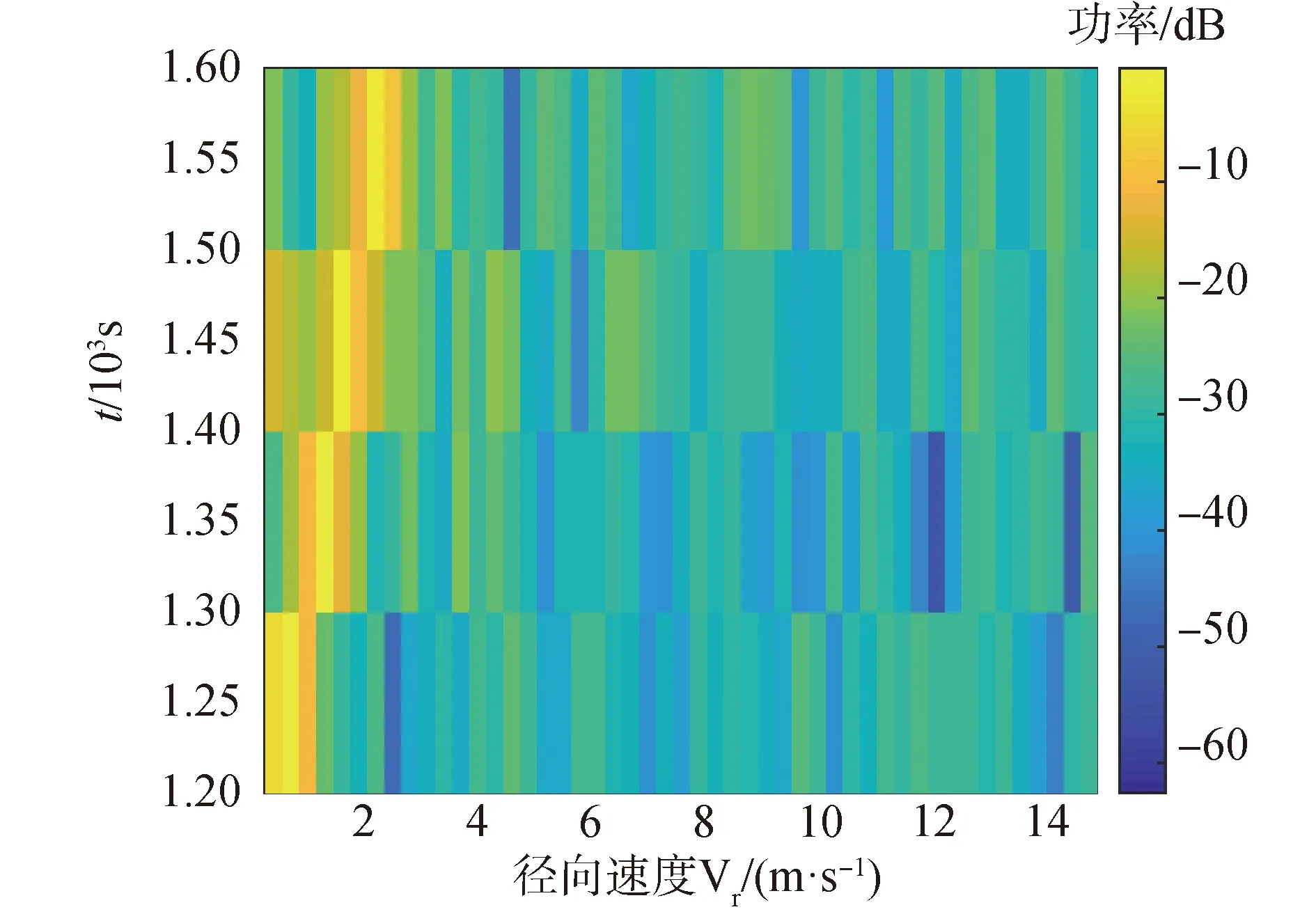
圖11 常規互譜目標速度估計Fig.11 Target velocity estimation of classic cross-spectrum

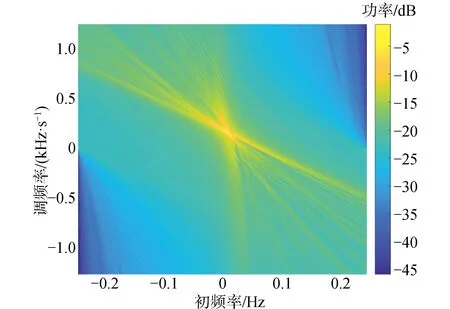
圖12 時頻互譜目標速度估計Fig.12 Target velocity estimation of time-frequency cross-spectrum

3.4 試驗數據處理結論

由上述對開源海試數據的分析研究可見，本文所提出的時頻互譜算法是有效的，其試驗數據處理結果與試驗理論值之間的誤差在10%以內，并且用時頻互譜法的輸出信噪比更高。

4 結論

1)對于水下目標輻射的低頻線譜可采用互譜法進行被動速度估計。相對于傳統互譜估計的目標徑向速度，本文提出的時頻互譜法可以直接估計目標的絕對速度。

2)時頻互譜法在提高信噪比增益的同時也降低了估計誤差，補充和拓展了傳統的互譜算法。