改進變分模態(tài)分解的核電廠軸承故障診斷

朱少民， 夏虹， 王志超， 彭彬森， 姜瑩瑩， 張汲宇

(1.哈爾濱工程大學 核安全與先進核能技術工業(yè)和信息化部重點實驗室，黑龍江 哈爾濱 150001； 2.哈爾濱工程大學 核安全與仿真技術國防重點學科實驗室，黑龍江 哈爾濱 150001)

核電廠中存在有大量的旋轉機械，如各類泵、汽輪機、電機、風機等，而軸承是旋轉機械中較為薄弱的環(huán)節(jié)，由于受到安裝、載荷、潤滑等因素的影響，軸承在運行過程中會發(fā)生各種類型的失效[1]。據統(tǒng)計，旋轉機械的故障中30%以上來自于軸承[2]，因此，需要采用有效的檢測技術對核電廠軸承的運行狀態(tài)進行評估。核電廠一般采用在線的方式對旋轉機械的振動幅值進行監(jiān)測，一旦超出閾值將采用頻譜分析技術對設備的振動信號進行分析并確定故障原因[3]，但是只有在故障程度發(fā)展到足夠大的時候才會被檢測出來，加大了被動停機的風險。因此軸承的早期故障檢測是關鍵，并在此基礎上制定預測性的維護策略。

在軸承故障早期，周期性的沖擊脈沖信號非常微弱，由于環(huán)境噪聲的影響，難以提取出故障特征[4]。根據工程實踐經驗，機械振動響應是多頻特征信號的疊加，因此可以采用信號分解和濾波的方式來提取故障特征，常用的信號分解方法主要有小波分解[5]、小波包分解[6]、經驗模態(tài)分解(empirical mode decomposition, EMD)[7]和局部均值分解(local mean decomposition, LMD)[8]等。但是小波和小波包是一種非自適應的分解方法，需要提前確定小波基函數和分解層數。雖然EMD和LMD能夠對信號進行自適應的分解，但是模態(tài)混疊現象使其應用受到了限制。集成經驗模態(tài)分解(ensemble empirical mode decomposition, EEMD)通過添加輔助白噪聲在一定程度上緩解了模態(tài)混疊問題[9]，但計算量急劇增加，添加的白噪聲無法完全被中和，不具有完備性。相對于遞歸式的模態(tài)分解方法，變分模態(tài)分解(variational mode decomposition，VMD)可以將信號分解成一組有限帶寬的固有模態(tài)函數(intrinsic mode function, IMF)，并在線估計其中心頻率，可以有效抑制模態(tài)混疊現象。

由于模態(tài)數和帶寬控制參數對VMD的分解效果具有顯著的影響，并且在傳統(tǒng)的VMD方法中，參數的取值是預先給定的，因此本文以最大加權峭度指標為目標函數，采用ABC算法對VMD參數進行優(yōu)化，并對加權峭度指標最大的敏感分量進行分析，從而提取軸承的早期故障特征。由于核電廠中的軸承數據較難獲取，因此本文采用仿真和實驗數據進行分析。

1 基于人工蜂群優(yōu)化的變分模態(tài)分解方法

1.1 變分模態(tài)分解

VMD是一種新的信號分解方法[10]，它的分解過程就是求解K個模態(tài)函數μk(t)，k∈{1,2,…,K}，使其估計帶寬之和最小，且各模態(tài)函數之和為輸入信號f(t)，因此，利用VMD對信號進行分解的過程可以用約束變分模型表示：

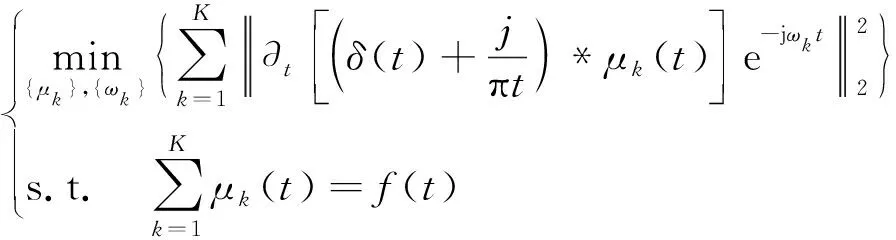
(1)

式中：μk(t)為各模態(tài)函數；ωk為各模態(tài)函數的中心頻率；δ(t)為沖激函數。

為了求解上述的約束變分問題，引入二次懲罰因子α和Lagrange乘法算子λ(t)。其中α可以保證在高斯噪聲存在的情況下信號重構的精度，λ(t)可以保證約束條件的嚴密性，則擴展的Lagrange表達式為：

L(μk(t),ωk,λ(t))=

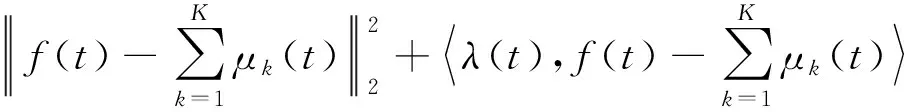
(2)

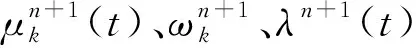
每個模態(tài)函數μk(t)和相應的中心頻率ωk的更新迭代過程為：

(3)

(4)

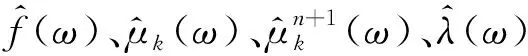
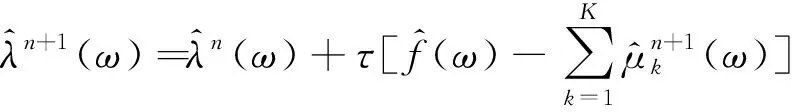
(5)

式中：τ為更新步長。直到滿足：

(6)

上述的迭代過程停止，最終得到K個具有獨立頻帶成分的模態(tài)函數。

從上述過程可以看出，VMD在分解過程中需要預先設置4個參數，分別為模態(tài)數K、帶寬控制參數(二次懲罰因子)α、更新步長τ和收斂誤差ε。其中模態(tài)數和帶寬控制參數對VMD的分解效果影響較大，而其他2個參數一般取默認值。

1.2 人工蜂群算法

人工蜂群(artificial bee colony, ABC)是根據蜜蜂覓食原理提出的群智能優(yōu)化算法[11]。ABC算法中將蜂群分為雇傭蜂、跟隨蜂和偵查蜂。在每一次食物源的搜尋過程中，雇傭蜂先發(fā)現食物源并記錄食物源的信息，然后跟隨蜂根據雇傭蜂提供的食物源信息按一定的概率選擇一個食物源。當一個食物源經過有限次搜尋之后仍然沒有被更新，那么該食物源將會被舍棄，相應的雇傭蜂變成偵查蜂并隨機尋找新的食物源。

每個食物源代表優(yōu)化問題的一個可能解，食物源的花蜜量代表相應解的質量，即適應度值fiti。在ABC算法求解優(yōu)化問題時，首先初始化種群，隨機產生SN個d維的初始解xi(i=1,2,…,SN)：

xi=lb+(ub-lb)·rand(0,1)

(7)

式中：ub、lb分別為xi取值的上限和下限，其中xi=[xi1xi2…xid]T。初始化之后，整個種群將進行雇傭蜂、跟隨蜂和偵查蜂的循環(huán)搜尋過程，直到滿足誤差要求或達到最大迭代次數。

雇傭蜂首先進行領域搜索，在已有食物源附近更新食物源位置：

x′ij=xij+φij(xij-xkj)

(8)

計算新解的適應度值fiti：

(9)

如果新解的適應度值優(yōu)于舊解，則雇傭蜂接受新解，否則將保留舊解。跟隨蜂再依據適應度值計算每個解被選擇的概率：

(10)

式中：k∈{1,2,…,SN}，且k≠i；j∈{1,2,…,d}；φij∈[-1,1]的隨機數；fi為第i個解的目標函數值；probi為第i個解被選擇的概率。隨后在區(qū)間[0,1]內產生一個隨機數，如果probi大于該隨機數，則跟隨蜂將按照式(8)產生新解并計算新解的適應度值fiti，若新解的fiti優(yōu)于舊解，則跟隨蜂接受新解，否則將保留舊解。如果一個解經過有限次循環(huán)后仍然沒有被更新，為了防止陷入局部最優(yōu)，該解將會被舍棄，相對應的雇傭蜂將變成偵查蜂并產生新解：

xij=xminj+rand(0,1)·(xmaxj-xminj)

(11)

式中xmaxj、xminj分別為第j維上的最大值和最小值。

1.3 基于改進VMD的軸承故障特征提取方法

本文以最大加權峭度指標為目標函數，采用ABC算法對VMD分解過程中的模態(tài)數K和帶寬控制參數α進行優(yōu)化，對加權峭度指標最大的敏感模態(tài)分量進行包絡譜分析并識別故障特征。在機械振動信號分析和特征提取過程中，采用的特征指標主要有熵、峭度、相關系數、振動烈度等，其中峭度和相關系數2個指標應用最為廣泛。峭度是一種無量綱指標，對振動信號中的沖擊分量極為敏感，因此它適用于沖擊測量，并已廣泛應用于機械設備的損傷監(jiān)測中。然而峭度只依賴沖擊信號的分布密度，如果以最大峭度指標為目標函數對VMD參數進行優(yōu)化，可能會忽略一些振幅較大但分布較為分散的沖擊分量。相關系數可以表征信號間的相似程度，但在沖擊信號檢測中容易受到噪聲的影響。因此，考慮到峭度和相關系數這2個指標的優(yōu)缺點，采用加權峭度指標作為目標函數對VMD參數進行優(yōu)化，加權峭度指標KCI定義為：

KCI=KI·|C|

(12)

(13)

(14)

式中：KI為信號序列x(n)零均值下的峭度值；N是信號長度；C為信號x(n)和y(n)之間的相關系數，文中表示各IMFs與原始信號之間的相關系數，其取值范圍是|C|≤1。考慮到ABC算法以最大適應度值fiti為優(yōu)化目標，按照式(9)中fiti的定義，優(yōu)化目標即為目標函數的最小值，因此本文以最小-KCI為優(yōu)化目標，則本文提出的基于參數自適應VMD的軸承故障特征提取方法的原理如圖1所示。

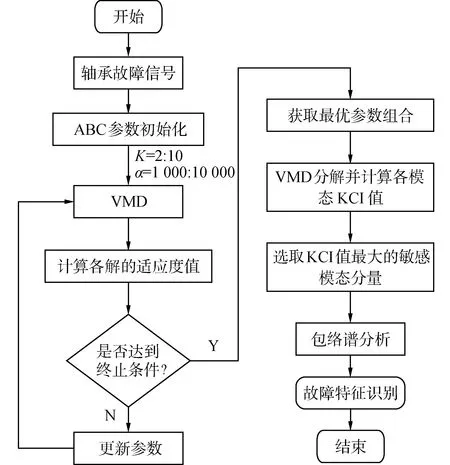
圖1 基于參數自適應VMD的軸承故障特征提取方法Fig.1 Flowchart of bearing fault feature extraction based on parameter adaptive VMD

首先，輸入軸承故障信號，初始化ABC算法參數，并且設置優(yōu)化參數的范圍；然后，對信號進行VMD分解，計算各解的適應度值。判斷是否達到迭代終止條件，如果沒有則更新參數繼續(xù)進行迭代，如果滿足終止條件，則輸出最優(yōu)的參數組合；最后，利用最優(yōu)參數組合對信號進行VMD分解，并對KCI值最大的敏感模態(tài)進行包絡譜分析，從而對故障特征進行識別。

2 軸承仿真信號分析

當核電廠中大型旋轉機械的軸承出現點蝕或缺陷故障時，零件之間的碰撞會產生周期性指數衰減的正弦沖擊信號。在故障早期，沖擊信號較為稀疏且微弱，很容易被強噪聲淹沒。為了對提出的軸承故障特征提取方法的有效性進行驗證，本文利用軸承內圈故障的仿真信號進行分析：

(15)

式中：x(t)為帶噪聲的模擬沖擊信號；s(t)為周期性沖擊信號；n(t)為高斯白噪聲；Ai為第i次沖擊信號的幅值，初始幅值A0=0.5，轉頻fr=10 Hz；h(t)為指數衰減的正弦信號，阻尼系數C=250，系統(tǒng)固有頻率fn=3 000 Hz，平均脈沖周期T=0.05 s;τi為第i次沖擊相對于周期T的微小波動，服從均值為零，標準差為0.5%倍轉頻的正態(tài)分布；軸承的故障特征頻率fs=1/T=20 Hz；加噪沖擊信號的信噪比SNR=-15 dB；信號的采樣頻率為12 000 Hz。則軸承內圈故障的仿真信號及其包絡譜如圖2所示。

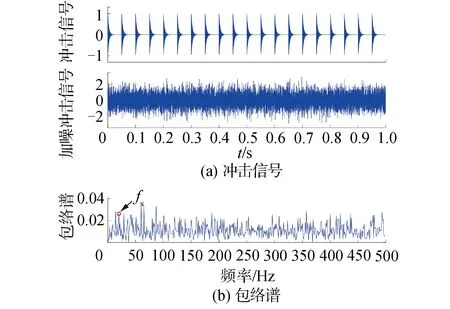
圖2 軸承內圈故障仿真信號及其包絡譜Fig.2 Simulation signal of bearing inner race fault and its envelope spectrum

從圖2可以看出，周期性脈沖信號幅值較小，基本淹沒在強背景噪聲中，從時域波形圖中很難觀察到沖擊分量，可以用來模擬軸承早期故障的微弱振動響應。雖然加噪信號的包絡譜中可以觀察到故障特征頻率fs，但是周圍干擾分量較多，在故障未知的前提下很難得出準確的診斷結果。因此利用本文提出的方法對加噪沖擊信號進行處理，設置ABC的食物源數量SN=10，最大迭代次數為10，則以最小-KCI為目標，求VMD分解最優(yōu)參數組合的ABC收斂曲線如圖3所示。

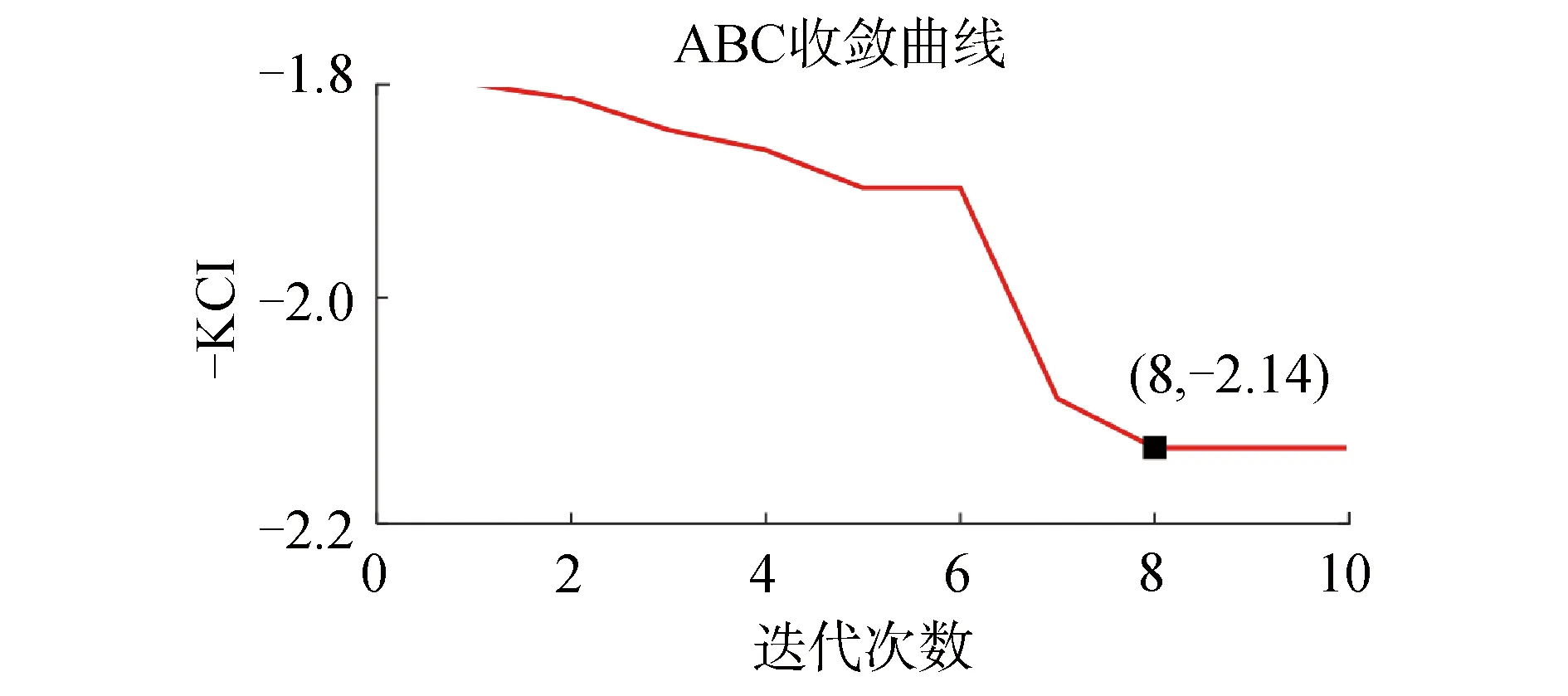
圖3 ABC收斂曲線Fig.3 ABC convergence curve

從圖3可以看出，ABC優(yōu)化的最大KCI值為2.14，相對應的模態(tài)數K和帶寬控制參數α的取值分別為2和1 500。采用最優(yōu)參數組合的VMD方法對加噪沖擊信號進行分解并計算各模態(tài)的KCI值，結果如圖4所示。將KCI值最大的IMF2作為敏感分量并對其進行包絡譜分析，從而提取故障特征。為了對KCI作為敏感分量選擇依據的有效性進行驗證，還對其他模態(tài)分量進行了包絡譜分析，結果如圖5所示。

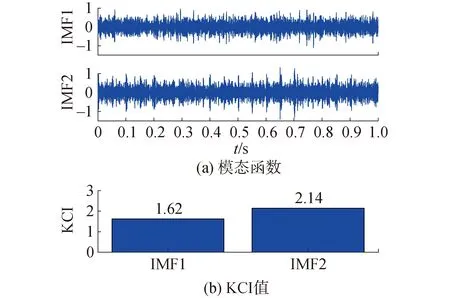
圖4 模態(tài)函數及其KCI值Fig.4 Modes decomposed by the optimal VMD and the corresponding KCI values

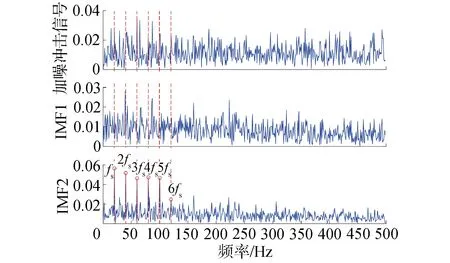
圖5 加噪沖擊信號及各模態(tài)的包絡譜Fig.5 Envelope spectrums of noisy impact signal and each modes

通過對比可以看出，IMF2幾乎包含了所有特征信息，與原始加噪沖擊信號相比故障特征頻率更為顯著，能夠清晰地觀察到故障頻率fs及其諧波(2fs、3fs、4fs、5fs、6fs)，而IMF1主要為噪聲分量，包絡譜中沒有觀察到明顯的故障特征。分析結果表明，將KCI作為敏感模態(tài)分量的選擇依據是有效的，該方法能夠有效地分析振動信號，提取出強背景噪聲中的微弱故障特征。

為進一步評估本文方法的特征提取效果，將該方法與EEMD、LMD和固定參數VMD的信號處理效果進行比較，將原加噪沖擊信號分別進行EEMD、LMD和固定參數VMD分解，其中VMD分解中模態(tài)數K和帶寬控制參數α分別取默認值4和2 000。然后以最大KCI值為依據選取敏感模態(tài)分量進行包絡譜分析，結果如圖6所示。

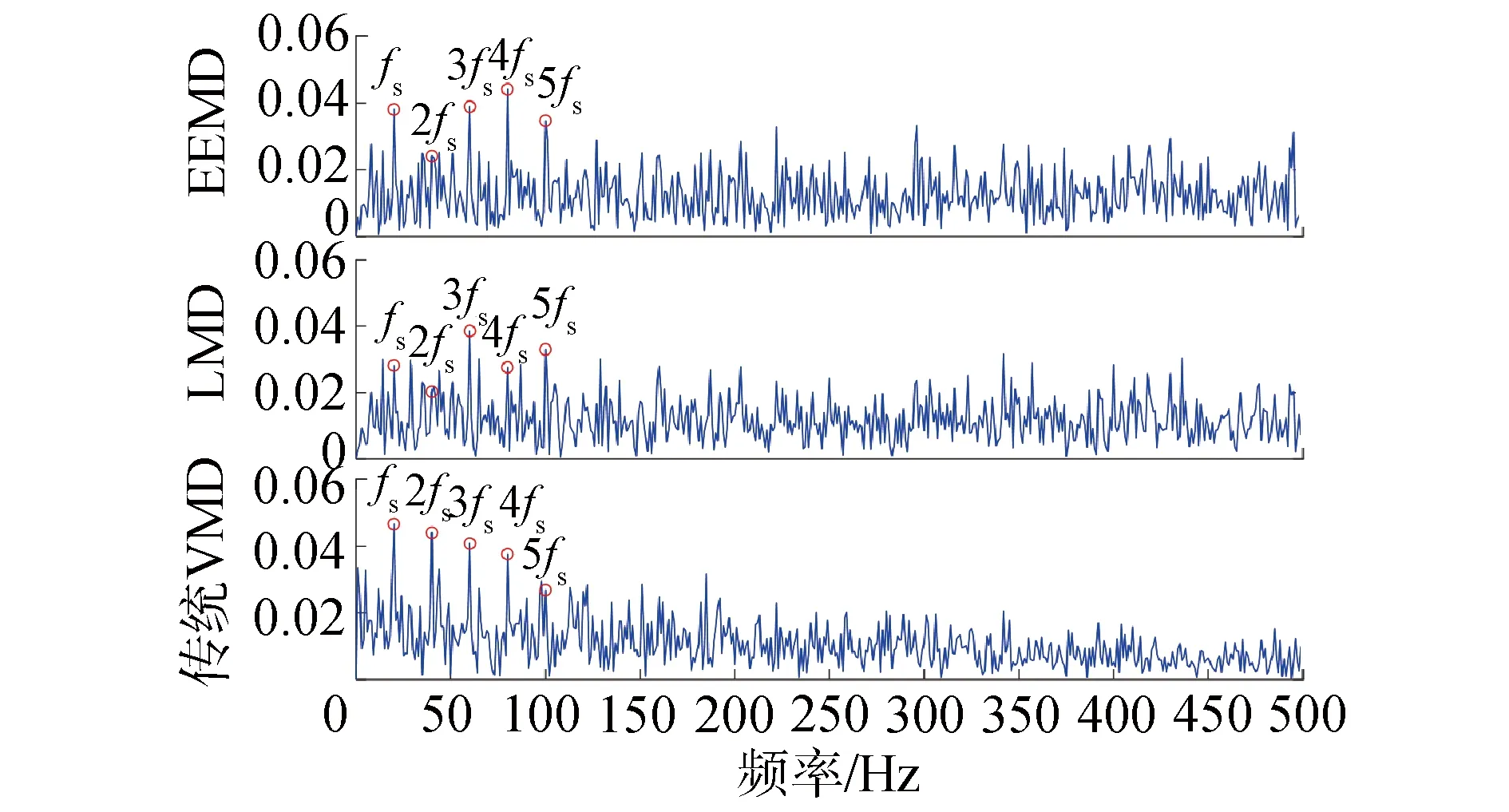
圖6 敏感模態(tài)分量的包絡譜Fig.6 Envelope spectrums of sensitive modes

EEMD、LMD和固定參數VMD方法均能夠在不同程度上識別出故障頻率fs及其諧波分量，但是3種方法故障特征頻率的幅值與本文方法相比要小，且均無法識別諧波分量6fs。其中EEMD方法中諧波分量2fs無法識別，LMD方法低頻處存在有大量的干擾分量，故障頻率fs和諧波分量2fs無法清晰觀察到。因此，本文方法針對沖擊信號的特征提取方面與EEMD、LMD、固定參數VMD方法相比具有更好的效果，為了進一步驗證該方法的有效性和工程應用價值，下一節(jié)將采用該方法對軸承故障的實驗數據進行分析。

3 實驗驗證

軸承內圈故障數據來自于XJTU-SY軸承加速壽命測試平臺[12]，實驗臺和故障軸承內圈如圖7所示，測試軸承的主要參數如表1所示。驅動軸轉速為2 400 r/m，采樣頻率為25.6 kHz，計算得到軸承外圈和內圈的理論故障頻率分別為123.32 Hz和196.68 Hz。

圖7 實驗臺及故障軸承內圈Fig.7 The testbed and the bearing inner race with defect

表1 測試軸承參數Table 1 The specification of test bearing

軸承內圈故障信號的時域波形和包絡譜如圖8所示，由于軸承處于早期故障階段，沖擊脈沖的幅值并未大量超出正常值，因此核電廠中的幅值監(jiān)測手段將很難檢測出故障，并且包絡譜中也未能獲取故障信息。然后利用本文提出的方法對軸承故障信號進行處理，ABC的參數設置與上文相同，則以最小-KCI為目標，求VMD分解最優(yōu)參數組合的ABC收斂曲線如圖9所示。

圖8 軸承內圈故障信號及其包絡譜Fig.8 Fault signal of bearing inner race and its envelope spectrum

從圖9可以看出，ABC優(yōu)化的最大KCI值為2.16，相對應的模態(tài)數K和帶寬控制參數α的取值分別為5和1 000。采用最優(yōu)參數組合的VMD方法對軸承故障信號進行分解并計算各模態(tài)的KCI值，結果如圖10所示。

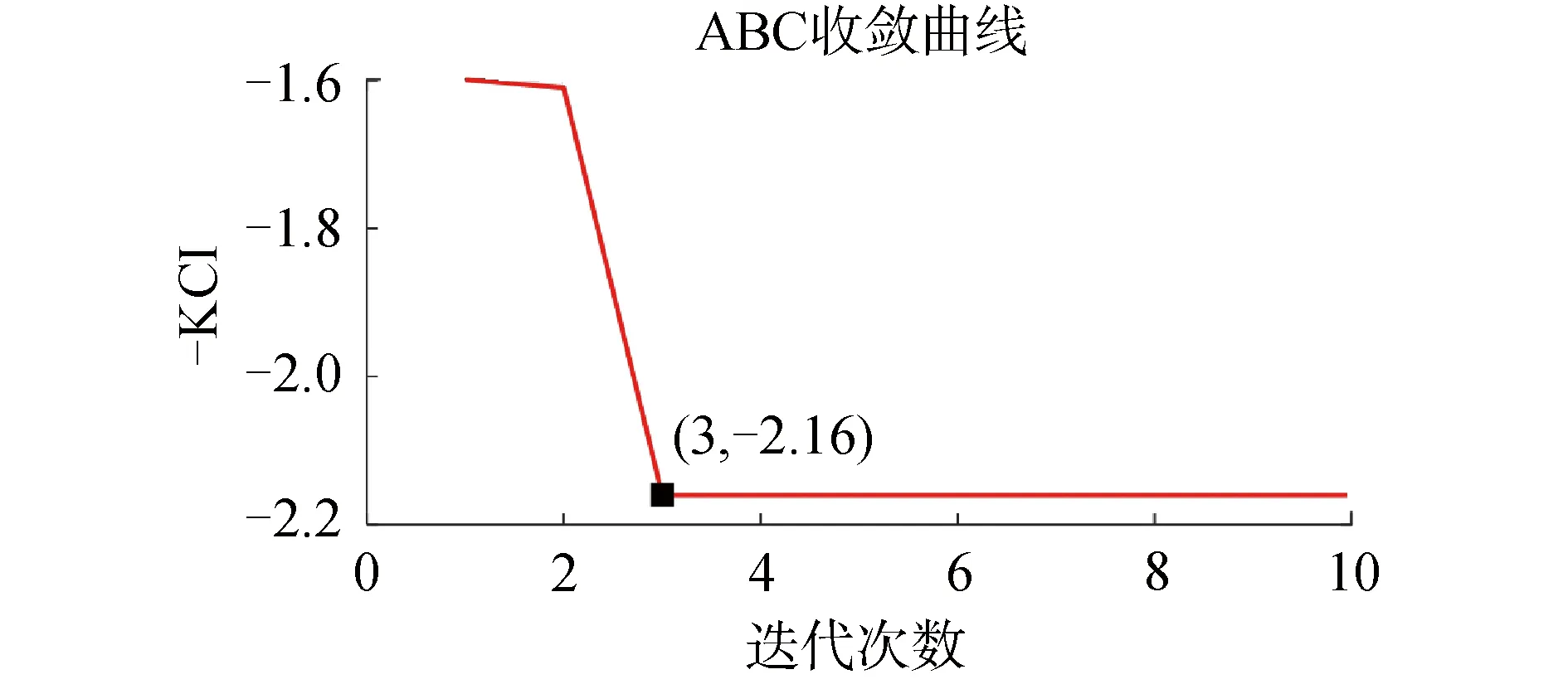
圖9 ABC收斂曲線Fig.9 ABC convergence curve

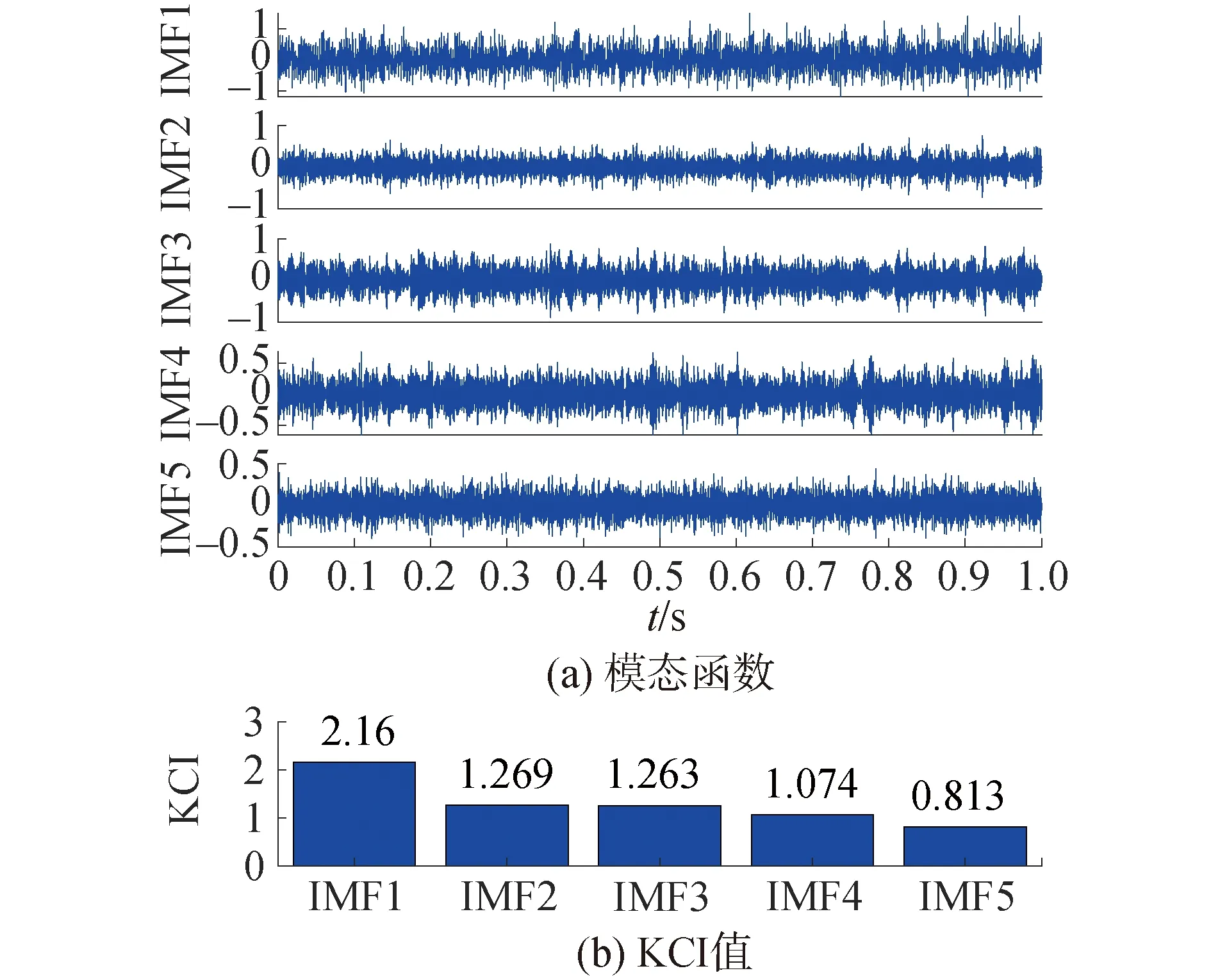
圖10 模態(tài)函數及其KCI值Fig.10 Modes decomposed by the optimal VMD and the corresponding KCI values

將KCI值最大的IMF1作為敏感分量并對其進行包絡譜分析。同樣，為了對KCI作為敏感分量選擇依據的有效性進行驗證，還對其他模態(tài)分量進行了包絡譜分析，結果如圖11所示。

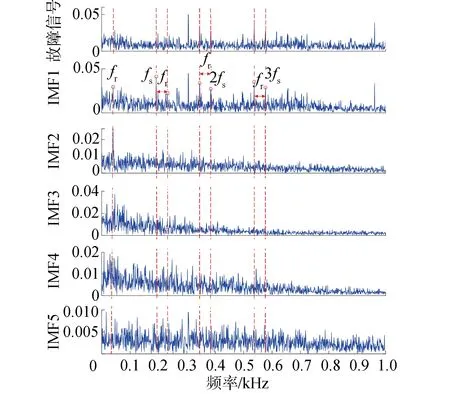
圖11 軸承故障信號及各模態(tài)的包絡譜Fig.11 Envelope spectrums of bearing fault signal and each modes

可以看出設備運行狀態(tài)的信息集中于所選的IMF1中，再次表明了將KCI作為敏感模態(tài)分量的選擇依據是有效的。與原始軸承信號相比，IMF1的包絡譜中故障特征頻率更為顯著，能夠清晰地觀察到轉頻fr、故障頻率fs及其諧波(2fs、3fs)，并且在fs、2fs、3fs附近均出現了轉頻fr的邊頻帶，表明故障特征頻率受轉頻fr的調制，軸承的內圈出現了局部缺陷故障，這與實驗結果是一致的。

將本文方法與EEMD、LMD和固定參數VMD的信號處理效果進行比較，各種方法獲取的敏感模態(tài)分量的包絡譜如圖12所示。EEMD和LMD方法均無法識別出故障頻率fs，而固定參數VMD方法能夠有效識別出轉頻fr、故障頻率fs及其轉頻fr的邊頻帶，但是無法識別故障頻率fs的諧波分量。因此，進一步驗證了本文方法在軸承內圈的早期故障識別方面比EEMD、LMD、固定參數VMD方法具有更好的效果。

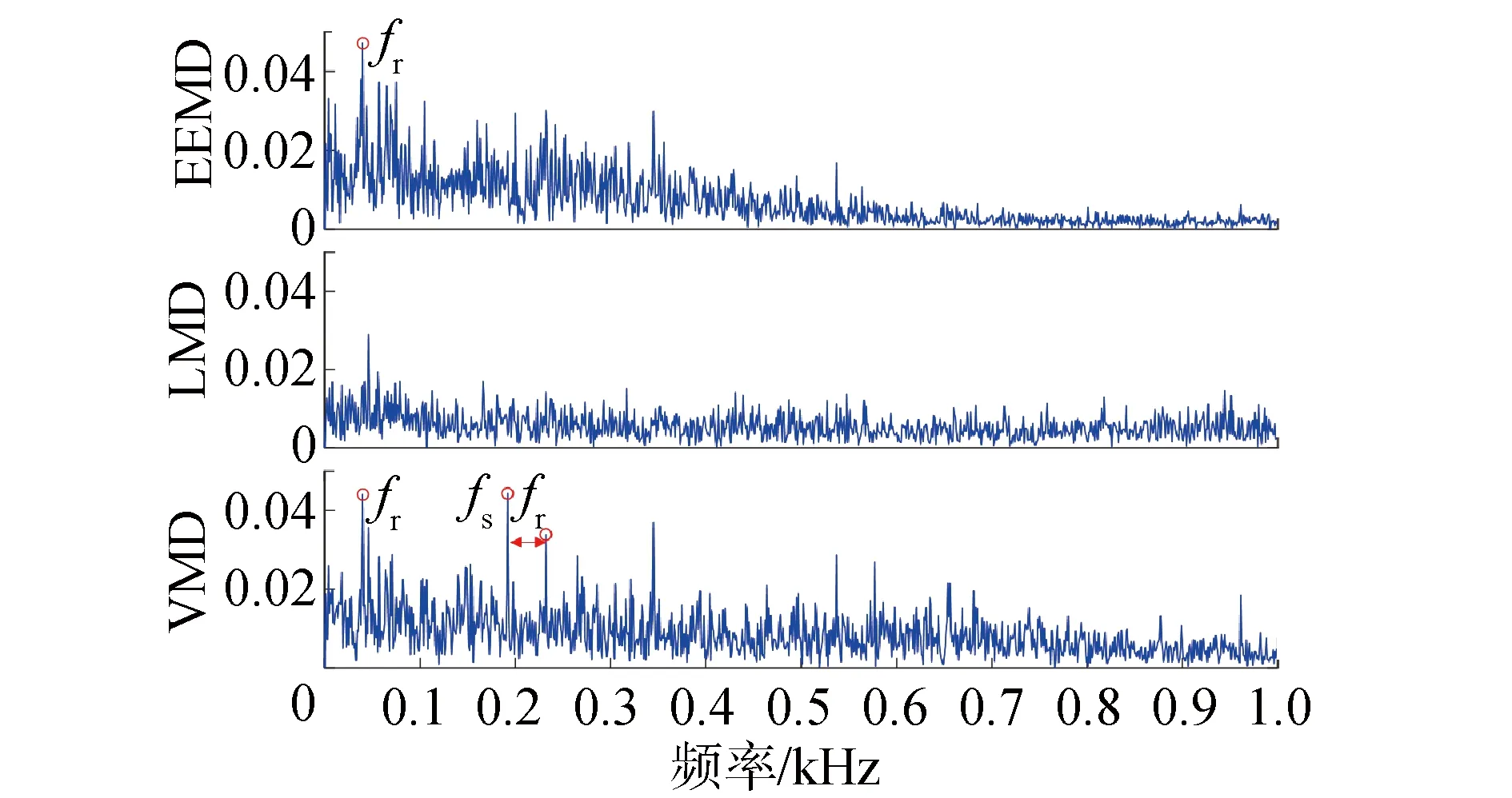
圖12 敏感模態(tài)分量的包絡譜Fig.12 Envelope spectrums of sensitive modes

4 結論

1)該方法克服了VMD的參數選擇問題，能夠自適應地獲取與待分解信號相匹配的模態(tài)數K和帶寬控制參數α。

2)ABC優(yōu)化過程中以加權峭度指標KCI為目標函數，不僅考慮了各分解模態(tài)的沖擊特性，還考慮了模態(tài)與原信號的相關性，可以有效避免重要特征信息的泄漏。

3)采用該方法分別對軸承內圈早期故障的仿真和實驗信號進行分析，均成功識別出故障特征頻率。通過與EEMD、LMD和固定參數VMD方法的比較，進一步驗證了該方法在早期故障特征提取方面的優(yōu)勢。

該方法對核電廠軸承的早期故障檢測具有一定的工程參考價值，在滿足高頻振動信號采集、傳輸和存儲要求的前提下，該方法可用于核電廠軸承在線故障檢測。下一步將針對該方法的故障可檢測范圍進行研究，以確定該方法在一定故障程度和噪聲強度下的適用性。