低碳經濟背景下中日韓郵輪航線設計
閔德權 劉圣坤


【摘 要】 為促進我國郵輪旅游產業綠色健康發展,選擇上海郵輪母港作為出發港,將日本10個城市的港口作為備選掛靠港,使用TOPSIS-熵權法對航線的競爭力進行評估;對郵輪的航行速度設定一個變化區間,以郵輪航線所掛靠港口的競爭力最大和單航次碳排放量最少為目標,建立雙目標規劃模型并使用LINGO軟件進行求解,最終求得滿足約束條件的最優航線及郵輪航速。
【關鍵詞】 郵輪航線;TOPSIS-熵權法;航速優化
0 引 言
隨著我國人民生活質量的不斷提高,旅游已經成為人們休閑的主要方式,郵輪旅游業也越來越受到國家的重視。2018年,《國務院辦公廳關于促進全域旅游發展的指導意見》提到:“推動旅游與交通、環保、國土、海洋、氣象融合發展。加快建設自駕車房車旅游營地,推廣精品自駕游線路,打造旅游風景道和鐵路遺產、大型交通工程等特色交通旅游產品,積極發展郵輪游艇旅游、低空旅游。”2021年,《國務院關于加快建立健全綠色低碳循環發展經濟體系的指導意見》明確要求:打造綠色物流,推廣綠色低碳運輸工具,加大推廣綠色船舶示范應用力度等;深化綠色“一帶一路”合作,拓寬節能環保、清潔能源等領域技術裝備和服務合作。
近年來,碳排放引起的全球變暖問題受到高度重視,是國際社會關注的熱點問題,無論是地區還是行業都應以低碳經濟為目標,使降低碳排放量與經濟發展同步進行。有關學者也對碳排放問題作出研究:許歡等[1]將船舶航速作為決策變量引入傳統的航線配船模型中,并且將船隊的CO2排放量作為優化目標之一,建立船隊利潤最大與碳排放量最小兩個目標最優的雙目標航線配船模型;李碧英[2]在分析國內外航運業能耗及碳排放現狀后,從管理、技術、政策、營運等方面提出了航運業低碳發展的途徑;張雪[3]歸納了船舶碳排放評價方法,提出了3種溫室氣體排放計量方法、手冊和船舶載質量計算法,建立了評價船舶溫室氣體排放的模型;呂靖等[4]選擇了3條代表性班輪航線,將船型選擇、船舶數量及航速作為決策變量,建立集裝箱班輪船隊總營運成本與碳排放成本之和最小的非線性規劃模型,并證實了該模型的有效性;鎮璐等[5]提出了一個有到港時間限制的郵輪航線和速度優化模型,優化船舶在ECA內外的航線及速度,以最小化總燃油成本,并引用西北大西洋沿岸一條代表性的郵輪航線,通過計算決策出合理的航行方案,并評估ECA對航運的影響,證明了模型的有效性和實用性。
本文在不考慮ECA的前提下,以在郵輪單航次中碳排放量最少和航線競爭力最大為目標,對中日韓郵輪航線進行優化設計,采用熵權法及TOPSIS法對掛靠港口的競爭力進行計算,并使用LINGO軟件對該模型進行求解。
1 郵輪港口掛靠綜合評價
1.1 港口評價指標
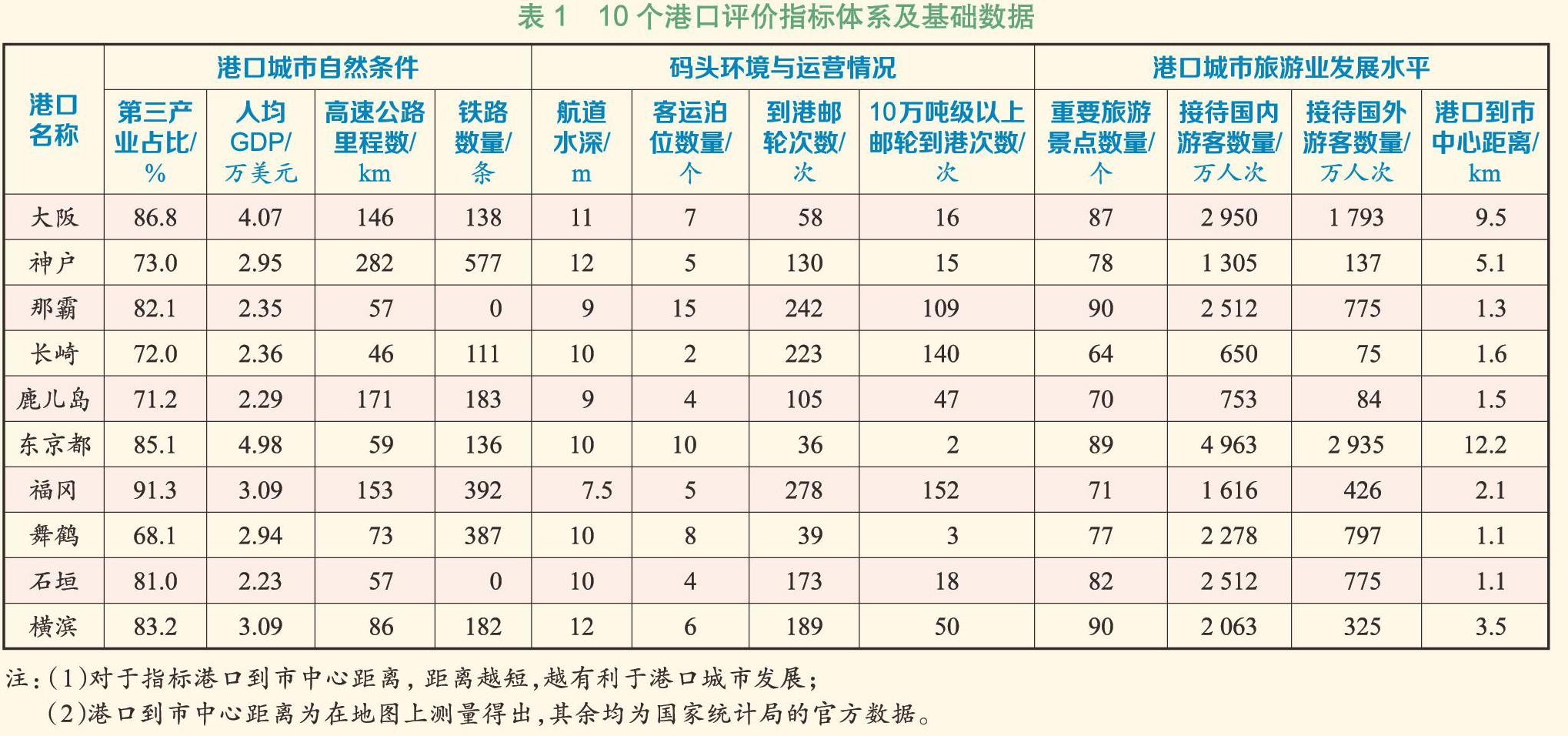
本文將港口城市的自然條件、碼頭環境與運營情況和港口城市旅游業發展水平作為3個一級指標,下設12個二級評價指標作為港口評價的依據。選取日本的12個城市作為備選掛靠港,以上海郵輪母港作為出發港,10個港口的評價指標體系及基礎數據見表1。
1.1.1 熵權法
根據信息熵的定義,可以用熵值來判斷某個指標的離散程度,其熵值越小,指標的離散程度越大,該指標對綜合評價的影響(即權重)就越大;如果某項指標的值全部相等,則該指標在綜合評價中不起作用。
(1)標準化處理
首先要對數據進行預處理,即根據指標體系的要求對冗余數據及異常數據等進行處理,得到初始數據矩陣。
假設有m個評價對象、n個評價指標,構成評價系統的初始數據矩陣,其中Aij? (i=1,2,…,m;? j=1,2,…,n)表示第i個評價對象的第j個評價指標,若歸一化后為 ,有如下兩個公式:
式中:max (Aj)是第j個指標的最大值;min(Aj)是第j個指標的最小值。若指標為正向指標,則選用式(1);若指標為負向指標,則選用式(2)。
本文有10個待評價港口、12個評價指標,其中C12為負向指標,其余為正向指標。用式(1)、式(2)對初始矩陣作標準化處理后,得到標準矩陣。
(2)計算指標的熵和權值
計算第i個評價對象的第j個指標的比重 :
計算第j個指標的信息熵:
其中0≤≤1。
計算第j個指標的權重wj:
根據式(3)、式(4)、式(5)求得12個指標的權重(見表2)。
1.1.2 TOPSIS法
TOPSIS法是通過檢驗評價對象與最優解、最劣解的距離來進行排序,若評價對象靠近最優解同時又遠離最劣解,則為最好,否則為最差。TOPSIS法的具體算法如下:
(1)原始矩陣正向化
在TOPSIS法中常見的4種指標見表3。
TOPSIS法就是要將所有指標進行統一正向化,即統一轉化為極大型指標。那么,需要將極小型、中間型及區間型等指標轉化為極大型指標。本文評價指標只有極大型指標和極小型指標,因此只需要對極小型指標進行處理。
極小型指標的處理有兩種方法:常見的方法是用足夠大的數值減去極小型指標的數值,即max-a;另一種方法是,若指標數值均為正數,那么也可使用,經過處理后的指標即為正向化指標。
(2)正向矩陣標準化
通過bij=對正向矩陣作標準化處理求得標準化矩陣B=(bij)m譶。
(3)確定正理想解和負理想解
定義正理想解= bij,xj為效益型屬性;
定義負理想解= bij,xj為成本型屬性。
(4)計算各港口的評價指標值
計算各評價對象到正理想解的距離與到負理想解的距離。需要注意的是,在TOPSIS軟件中默認各項指標的權重相同,但在實際的評價中指標都是有各自的權重,因此應用權重對公式進行修正后得到、:
計算各港口的評價指標值 。
由以上公式得到各港口的評價指標值,即競爭力。由于上海港為出發港、釜山港為必靠港,為排除這兩港口城市的影響,港口競爭力設為0。12個掛靠港的競爭力見表4。
2 郵輪航線優化模型
2.1 假設條件
(1)將郵輪從上海郵輪母港出發到再次抵達上海港這一行程作為一個航次,且在上海港的停靠時間為0。
(2)各掛靠港只能掛靠一次。
(3)郵輪的航行速度范圍為15~21 kn。
(4)掛靠港口的停留時間與港口競爭力數值有關。
(5)郵輪每航次的碳排放量只考慮在海上航行過程中因使用燃油所產生的碳排放。
(6)郵輪在航次過程中必須停靠釜山港。
(7)因為上海郵輪母港和釜山港必須停靠,所以將兩個港口的競爭力設為0,且郵輪在釜山港的停留時間設為10 h。
(8)由于日本各港口之間存在距離過短的情況,為保證乘客在郵輪上有足夠的休息和娛樂時間,不允許郵輪在港口之間距離低于400 n mile的航段航行。
(9)本文不考慮現存中日韓郵輪航線的影響。
2.2 航速與燃油消耗量及碳排放量的關系
2.2.1 郵輪每航次的燃油消耗量
在船舶的燃油消耗中,主機燃油消耗約占87%,副機燃油消耗約占11%,剩下的則為鍋爐燃油消耗,因此可以將船舶主機和副機的燃油消耗近似地作為船舶的全部燃油消耗。[6]主機燃油消耗與航速相關,副機和鍋爐等燃油消耗則與航速無關。
主機油耗為
式中:G1為主機每小時燃油消耗量,kg/h;u為船舶機能系數,是一個常數;k為主機的燃油消耗率,g/(kW穐); v為船舶航行速度,kn。
因為副機燃油消耗G2與航速無關,所以將副機燃油消耗量看作主機燃油消耗的1/8,因此每航次燃油消耗G為
式中:t為航行時間,t= (S為該航次的航行距離),因此式(10)可表示為
燃油消耗率k取值170 g/(kW穐)。
2.2.2 單航次排放量
航運的排放量受一定時間內船舶燃油消耗量和碳排放因子的影響,本文采用的碳排放因子為3.17,即1 t船用燃油排放3.17 t的CO2,因此船舶碳排放量為
2.3 模型相關參數說明
Z為所有港口的集合,Z={1,2,…,n};V為郵輪航行速度的集合,vij為從港口i至港口j的航行速度,vij∈V,V={15,16,…,21};Sij為港口i到港口j之間的航行距離;tij為從港口i航行至港口j所用的時間,且tij=;wi為港口的綜合競爭力,競爭力越大所停留的時間越長;ti為郵輪在港口i的停留時間,該時間與港口的綜合競爭力有關;xij為郵輪是否從i港航行至j港,若是則為1,否則為0。
2.4 構建模型
構建雙目標航線優化模型,該模型的目標函數分別為郵輪單航次航線競爭力最大和航次碳排放量最少。
目標函數:
約束條件:
式中:i, j∈Z; i≠j; yi,yj≥0; xij∈{0,1}; vij∈V。
式(13)表示郵輪航線的競爭力最大;式(14)表示每航次的碳排放量最少;式(15)表示該航線為單向環形航線;式(16)表示該航線之間不含子巡回航線,即不存在脫離主航線的其余航線;式(17)表示必定掛靠釜山港以形成中日韓航線;式(18)規定了每航次要在限定時間內完成。
3 計算結果
各港口的停靠時間由各自的綜合競爭力決定,因為上海港不計入掛靠港,所以掛靠時間為0,并設定釜山港掛靠時間為10 h,各港口停留時間見表5。
郵輪運營最主要的目標還是盈利,因此航線競爭力應盡可能地大,以便吸引更多游客。對上述兩個目標函數賦予權重,航線競爭力與碳排放量兩個目標函數的權重比為2∶1,另設船舶機能系數u=1。運用LINGO軟件對該模型進行求解,計算結果見表6。
由表6可以看出:
(1) 7~8 d的最大航線競爭力為4.8,選用的航速為21 kn,但其碳排放較高,為769 t;最小碳排放量為460 t,選用的航速為15 kn,但其航線競爭力較低,僅為4.62。可見,選用固定航速雖然在某一方面可以達到令人滿意的結果,但在其他方面卻遠低于預期。因此,在設定航速范圍后,運用LINGO軟件計算得到航速為17.2 kn時其航線競爭力和單航次碳排放量分別為4.66和473 t,均能達到較為滿意的結果,其航線為:上海―釜山―東京―福岡―那霸―上海。
(2) 9~10 d的最大航線競爭力為4.57,選用的航速為18 kn,但其碳排放量較高,為636 t;最小碳排放量為382 t,選用的航速為15 kn,但其航線競爭力過低,僅為3.79。運用LINGO軟件計算得到航速為15.9 kn時其航線競爭力和單航次碳排放量分別為4.3和475 t,均能達到令人滿意的結果,其航線為:上海―長崎―那霸―福岡―東京―釜山―上海。
4 結 語
在環境問題日益受到關注的今天,郵輪公司不僅要考慮自身的利益,還要注意保護環境,減少碳排放。本文以郵輪航線競爭力最大和航次碳排放量最少為目標建立非線性模型,對“到達時間”和“掛靠港選擇”進行約束,并運用LINGO軟件對實例進行論證,最終得到航線競爭力足夠大及單航次碳排放量足夠低的航線。此外,因為郵輪的碳排放量與燃油量是正向關系,因此碳排放量的減少還可以減少燃油的消耗,降低成本,達到雙贏的效果。
參考文獻:
[1] 許歡,劉偉,張爽.低碳經濟下船舶航行速度選擇[J].中國航海,2012(2):98-101.
[2] 李碧英.航運業節能減排現狀及其低碳發展的途徑[J].工程研究,2012(3):260-269.
[3] 張雪. 船舶大氣污染物評價方法研究[D]. 武漢:武漢理工大學,2010.
[4] 呂靖,毛鶴達.硫排放控制區和碳排放限制下的班輪航線配船模型[J].大連海事大學學報,2017(1):101-105.
[5] 鎮璐,孫曉凡,王帥安. 排放控制區限制下郵輪航線及速度優化[J]. 運籌與管理,2019(3):31-38.
[6] 薛穎霞,邵俊崗.低碳經濟背景下班輪航線配船[J].中國航海,2014(4):115-119.

